高铁列车停靠站客票收入率分类及收入预测研究

张 永， 朱建生， 吕晓艳， 贾新茹， 王炜炜(. 中国铁道科学研究院 研究生部， 北京 0008； . 中国铁道科学研究院 电子计算技术研究所， 北京 0008)

在铁路实际客票收入清算工作中，管理部门依据列车历史收入情况估算出新的运行图中列车各分站客票收入，作为这个铁路局下一阶段的收入目标。同时，为了使各站收入目标具有说服力，管理部门会依据列车和其停靠站属性设计决策表，明确标注不同属性组合的列车的停靠站收入情况。

在清算系统设计过程中并未考虑上述功能[1-5]，只是根据清算指标和运营数据进行统计分析。在现有的客票收入影响因素分析和预测的研究中[6-8]，研究者通过影响列车整体客票收入的因素对未来收入进行经验推测或简单的回归计算，没有考虑列车分站信息对收入的影响，也没有考虑将这些信息进行归纳和分类。因此在决策表构建过程中会出现如下问题：首先目前对与分站收入相关的信息进行离散化处理时，使用等频或人工干预方法，易造成大量数据不一致现象，影响预测结果；另外传统做法不能从离散化的分类结果中得到准确合理的收入率取值，无法满足业务需求。本文利用2016年1月至10月中国铁路总公司下发的客运运行图中直通高铁列车分站信息，提出高铁列车停靠站客票收入率分类及客票收入预测模型，并以2016年11月新运行图中的高铁列车各停站日均客票收入率及其沿途各站所属铁路局收入总和为校验数据，验证了本文方法的分类及预测精度。

1 数据的离散化处理

第i趟列车日均客票总收入为Pi(i=1,2,…,N),其中N为总开行列车数。分站收入为pij(j=1,2,…,Ki)其中Ki为第i趟列车的总停站个数。则列车停靠站收入率ri为

ri=pij/Pi

( 1 )

目前铁路客票营销系统中与高铁列车停靠站收入率相关的信息有4个：停靠站距终到站距离、停靠站等级(停靠站日均发送量)、停靠站站序和列车离开停靠站时刻。将这4类影响因素作为因素变量，将客票收入率作为目标变量。为满足分类算法要求，需要将上述连续变量离散化，同时，数据离散化可以有效克服数据中隐藏的缺陷，避免极端值影响结果。

离散化算法分为无监督和有监督算法[9]。这两种算法主要的区别是有监督算法在进行离散化的过程中参考了目标变量，无监督算法则没有。无监督离散化算法有等频、WPKID和基于聚类的算法等；有监督学习算法有CACC算法、ChiMerge算法、Hellinger算法和基于信息熵的离散化算法等。

1.1 目标变量离散化

目标变量只能通过无监督算法进行离散化，但是上述无监督离散化算法忽略了数据分布信息，区间边界的确定不具有代表性，会影响因素数据进行监督离散化处理的过程中切分点的确定。对于上述问题，本文提出一种基于K-means和类-属性相关离散化[10]CACC(Class-Attribute Contingency Coefficient)算法的无监督离散化模型，K-means-CACC模型。CACC是一个自底向上的算法，它充分考虑了数据的分布，通过下式，计算各个待选区间中目标变量分布的相关性

( 2 )

式中：M为样本总数；n为切分区间的个数；qir为目标变量第i类，切分区间[dr-1,dr]中的样本数；Mi+为目标变量i中的样本数；M+r为切分区间[dr-1,dr]中的样本数；S为目标变量分类个数。算法具体步骤

Step1将待切分连续数据集升序排序，将相邻点的中值作为备选切分点放入集合B中；切分点结果集为D。设置全局CACC相关性变量，记为G，其初始值为0；设置最大切分点个数为M/(3·S)。

Step2迭代阶段：如果B中切分点不在D中，根据式( 2 )计算此点切分点两侧区间的相关性。将相关性最大的切分点插入到D中，并且将此相关性结果更新到全局变量G。

Step3当Step2中计算的相关性结果不再变化或者切分点个数大于等于设置的最大切分点时，算法结束。

模型的主要思想和流程如下：首先，将收入率进行等宽分割，本文中选取的宽度为0.01。然后，将收入率切分点与在这个范围内的样本密度作为输入，利用K-means进行聚类,这样有利于将具有不同数据密度的收入率区间区分开来。利用calinski-harabasz[11]指数确定K值，此指数从簇内的稠密度和簇间的离散度来评估聚类的效果，指数最大值所对应的聚类个数为最优聚类个数。本文运用Python2.7和science-kit机器学习算法包分别实现CACC算法和K-means算法。

聚类结束后，将所得到的聚类标签和收入率作为CACC的输入，这是对聚类结果的一次修正，使其聚类边界更加明确，这可以保证收入率与聚类标签相关性最大的被划分为一组。表1为目标变量离散化结果。

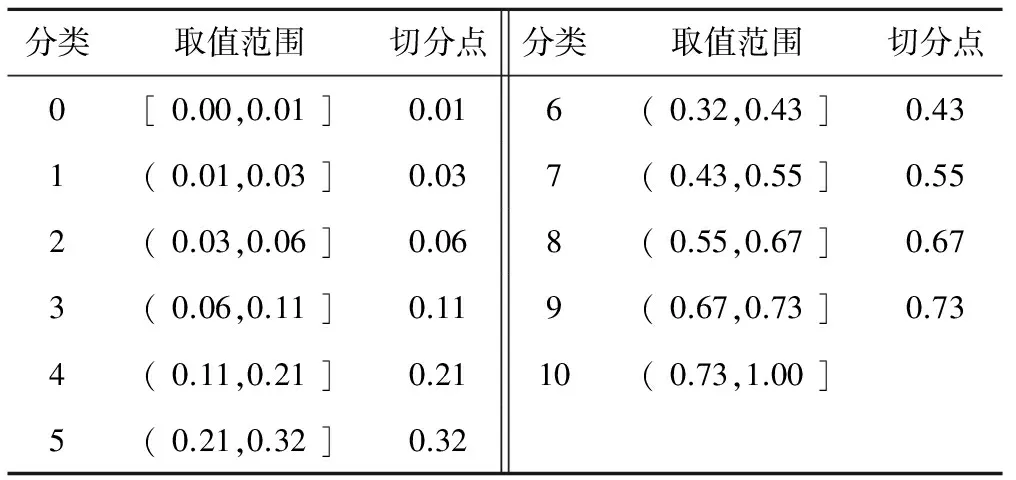
表1 目标变量离散化结果及切分点

1.2 因素变量离散化

根据目标变量离散化结果，采用CACC[10]算法可对因素数据进行监督的离散化，该算法被证明在后续的决策树算法中准确率更高[9]。

在对因素数据进行离散化处理之前，先处理列车离开停靠站时间这一数据：过了整点没有到半点的时刻，如08:13，记为8.5；而过了半点没到整点的时刻，如08:57，记为9。表2为因素数据离散化结果。

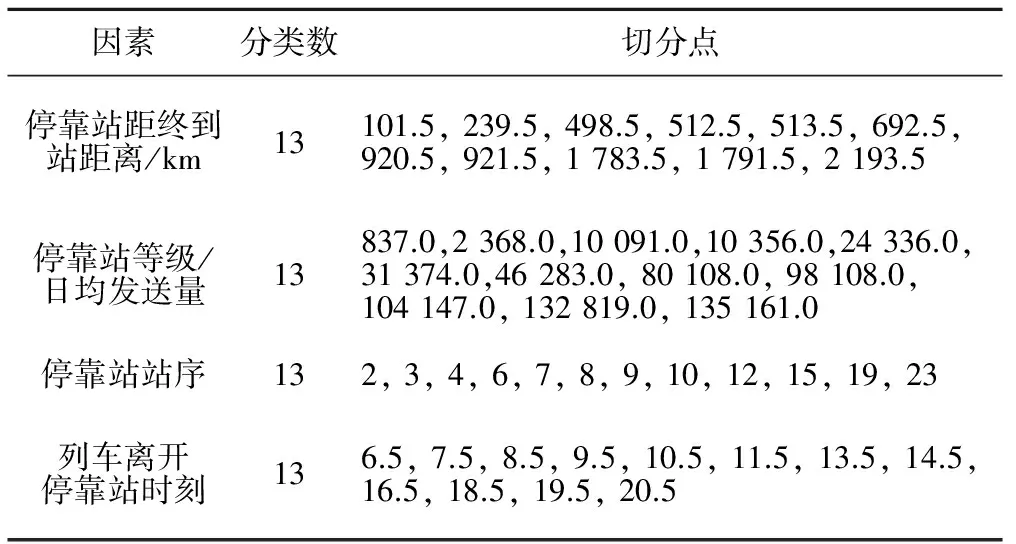
表2 高铁列车因素变量离散化结果及切分点

2 基于误差区间交集和样本密度的最优收入率选取

为满足业务部门需求，还需在每个收入率分类中，选取能满足一定误差范围的最优收入率准确取值，这一取值应使一个分类中，在误差范围内样本数达到最大。本文设计了一个基于误差区间交集和样本密度的最优收入率选取算法，其在给定的误差范围内，计算每个类中每个值的误差范围，并对它们进行交集运算，统计其中的样本数，最终得到数据密度最大的区间，计算其中值，便可以得到这个最优值。具体来说，设在第k个收入率分类中，对应N个实际收入率，即y0,k,y1,k，…，yj,k，…，yN,k和对应收入率的样本个数m0,k,m1,k，…，mj,k，…，mN,k，每一个收入率都存在一个值x0,k,x1,k，…，xj,k，…，xN,k，使得其在误差范围[b,a]内，满足相对误差，即

b≤xj,k-yj,k≤a

( 3 )

得x0,k,x1,k,…,xj,k,…,xN,k满足如下集合

A={xj,k|xj,k∈[b+yj,k,a+yj,k]}

( 4 )

显然如果两个集合存在交集，则满足交集部分的取值覆盖了两个集合所有的样本数。因此，在一个目标变量分类中，只需要计算式( 4 )中各个取值区间的交集中覆盖收入率样本密度最大的那个交集即可。算法步骤为：

Step1第一重迭代开始，在{A0,k,A1,k,…,Aj,k,…,AN,k}中逐次取Aj,k;

Step2Aj,k为此次迭代的初始化交集初始集合；

Step3计数器初始化为集合Aj,k所对应的样本数；

Step4i=j+1；

Step5第二重迭代开始，在{Ai,k,…,AN,k}中取Ai,k；

Step6初始集合Ai,k的交集存在，则用交集更新初始化集合，计数器累加所对应的样本数Nj,k；

Step7更新和保存计数器值最大的交集；

Step8第二重迭代结束后，计数器归零，返回Step1；

Step9所有迭代结束后，得到一个交集的集合，如果初始化时每个收入率对应的样本数相同，且计数器最终得到的值也为这个样本数，则表明在误差范围内数据无交集，计数器没有累加，最优值为全部数据的均值；否则，利用交集覆盖的区间样本数除以它所覆盖区间的长度得到样本密度，样本密度最大的为最优值所在的交集，本文取中值为最优值。

利用训练集计算出每个分类对应的最优值，当利用测试集进行验证时，使预测分类与这些最优值相对应，这样不仅可以为决策者提供一个参考的分类(离散化后为收入率取值范围)，也为其提供了一个参考的收入率取值。本文利用Python2.7实现上述算法，并根据业务需求将误差设定为[-5%,5%]。表4为最优收入率的选取结果。

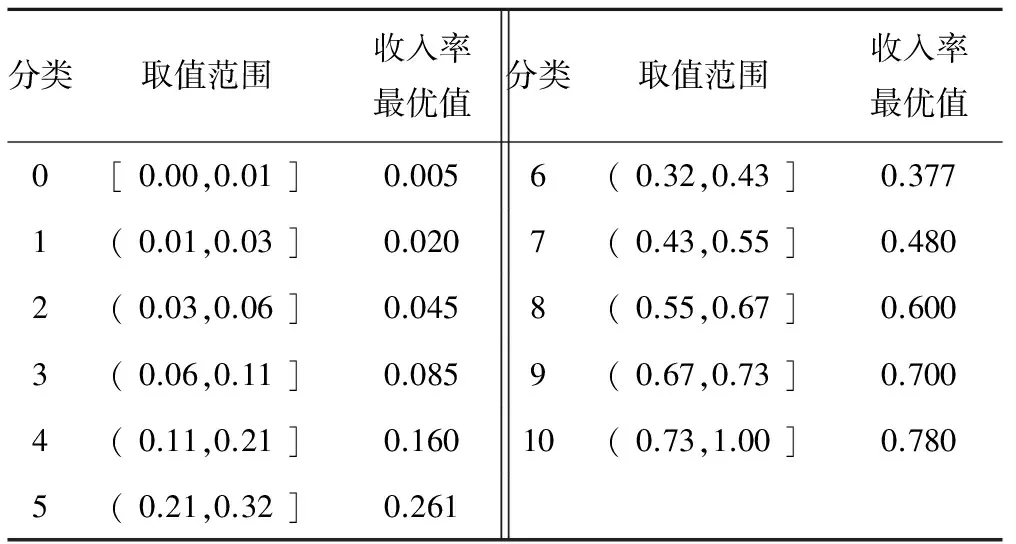
表4 每类中最优收入率选取结果

3 随机森林算法

随机森林算法是由Leo Breiman[12]于2001年提出来的。这个算法主要是通过随机重采样技术bootstrap进行行采样和随机子空间的思想进行特征的选取，构建多个互相没有关联的决策树，通过投票得到最终分类结果。具体算法流程为：

Step1当训练集进入算法之前，利用bootstrap方法进行行随机采样，对于大小为N的样本，随机地有放回地选取大小为k(k≪N)的样本，随机选取多个这样的样本就构建多个决策树。

Step2在全部的M个特征中，每一颗树的每一个节点随机抽取m(m≪M)作为决策树的决策属性，每次树进行分裂时，从这m个特征中选择最优的。

Step3利用决策树算法C4.5[13]对每棵决策树进行分类，使决策树进行最大限度的增长，不做任何剪枝操作。使用C4.5算法的主要原因是，其利用信息增益率进行节点的分裂，防止了选择属性时偏向选择取值多的属性的不足。

Step4将生成的多棵分类树组成随机森林，用随机森林算法分类器对新的数据进行判别与分类，分类结果按树分类器的投票多少而定。分类器投票式为

( 5 )

式中：H(x)为组合分类模型；hi(x)为单个决策树模型；Y为目标变量；I(·)为示性函数。

本文将前面训练集中因素和目标变量离散化的结果作为随机森林算法的输入，构建一个分类模型。测试集因素变量离散化结果输入到模型，得到预测分类结果。

在分类模型的构建过程中，笔者还计算了输入因素的重要性。在每次构建决策树后利用未被选中的样本进行预测，得到误差ri；之后加入未被选中的因素加入决策树，利用同样的样本进行预测，得到误差rj；则因素重要性指数I为(ntree为决策树的个数)

I=∑(ri-rj)/ntree

( 6 )

经过计算，可以得到4个因素的重要性排名，见表5。

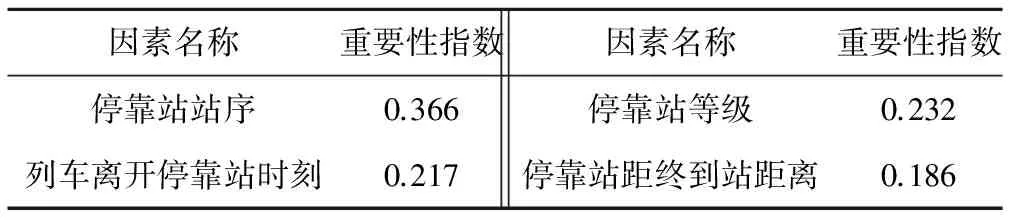
表5 因素重要性排名

由表5可知停靠站站序对于收入率分类的影响最大，其次是停靠站等级和列车离开停靠站的时刻，而停靠站距终到站距离对结果的影响最弱。

在预测结束后，其分类结果与训练集目标分类相对应，得到相应的最优收入率，比如预测收入率分类为第2类，在训练集中收入率的第2类最优收入率为0.045，则预测结果中此类的最优收入率为0.045。

近几年，随机森林算法在很多领域都发挥了重要的作用[14]。在本文中，笔者利用随机森林算法主要是考虑了其自身的一些优点：(1)由于在每次迭代之前引入随机采样，这使得算法不容易陷入过拟合并且具有很好的抗噪能力。同时，由于很好地解决了过拟合问题，在算法执行之前和结束不用再进行前或后的剪枝处理。(2)由于采取了随机子空间的方法进行特征选取，使得在进入算法前不必再进行影响因素选择等预处理。

4 算法有效性验证

为了验证本文中利用和提出的算法有效性，从三个方面对离散化算法、分类算法和最优收入率选取算法进行有效性和精度的对比验证。

(1) 分类精度评估

利用Kappa指数[15]评估分类精度。Kappa指数可用来检验分类的精度是否在可接受范围内，计算为

( 7 )

此算法利用实际收入率分类和预测的收入率分类频数建立一张二维表，Pii为对角线二者完全一致占样本数的比值，Pi+和P+i分别为第i个检验数据点的合计数和列合计数占总样本数的比值。在Landis和Koch的论文中[15]，他们提出Kappa值在0.21至0.40之间被认为是可接受的；在0.40至0.60之间被认为是中等的；在0.61至0.80之间被认为是精度较大的；大于0.81被认为是完美的分类。

(2) 分站收入率预测精度评估

利用第2节提出的基于误差区间交集和样本密度的最优收入率选取算法得到各类中最优收入率。从业务需求角度出发，在全部的10 369个高铁列车分站样本中，分站收入率预测精度为预测的各站客票收入率与实际客票收入率的绝对误差在[-3%,3%]以内的样本数占总样本数的比例。

(3) 各个铁路局收入预测精度评估

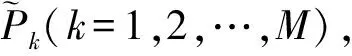
( 8 )

根据式( 8 )计算相应分站收入，并且根据分站不同所属铁路局(开行高铁的13个铁路局)对收入进行求和。在对比部分，笔者也考虑了在不同算法下，各个停靠站所属局获得的实际总收入与预测总收入的百分误差。

4.1 离散化算法有效性验证

4.1.1 目标变量离散化算法有效性验证

为了验证模型的有效性，保持模型中的其他模块方法不变，只是将目标变量离散化的方法分别替换成对比实验中的等频，WPKID和聚类算法这3种无监督离散化方法。为了验证CACC能否改进K-means聚类算法的离散化精度，保持数据中的分布信息，在对照的聚类离散化方法中选取K-means聚类算法。

由表6和图1可知，就本文讨论的问题而言，K-means-CACC目标变量离散化方法相比于其他方法能够提高预测的分类精度、收入率和收入预测精度。也可以看出，K-means聚类算法经过CACC的优化，离散化准确度得到提高。

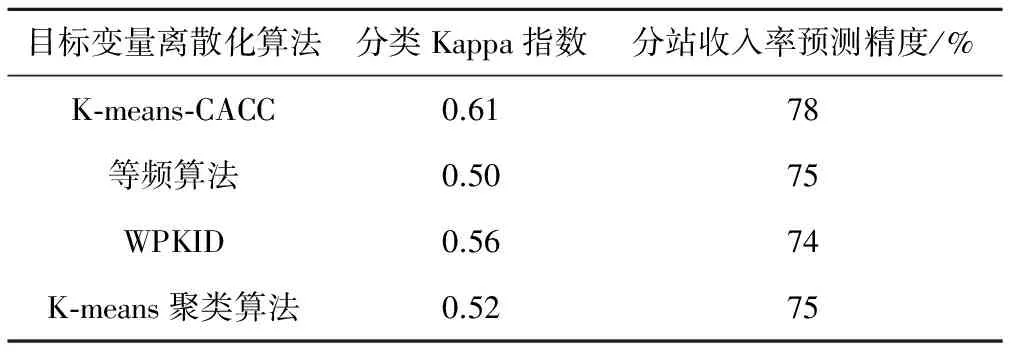
表6 目标变量离散化算法预测结果对比

4.1.2 因素变量离散化算法有效性验证

虽然文献[9]验证了CACC算法在决策树算法中的优势，但对于本文讨论的问题，本节再一次进行验证，将CACC算法分别与ChiMerge算法、基于信息熵的离散化算法、基于Hellinger的算法等相比较，结果见表7。

表7 因素变量离散化算法预测结果对比

由表7和图2可知，CACC算法较其他监督的离散化算法在分类精度和收入预测精度上表现更优异。

4.2 分类算法有效性验证

为了验证文中随机森林算法的使用是否合理，是否较其他分类算法能突出其优点，具体做法是将随机森林算法的分类预测结果的Kappa指数分别与SVM算法、C4.5决策树算法和Adaboost分类算法的结果的Kappa指数相比较。表8是验证结果。

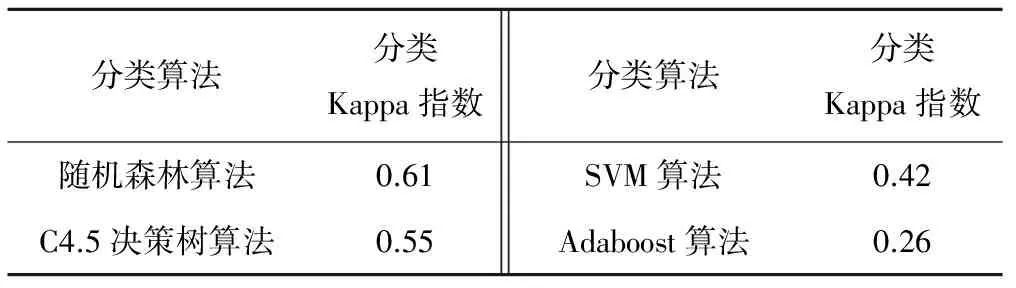
表8 不同分类算法预测精度对比

由表8可知，相对于其他分类算法，随机森林算法在分类预测方面有着较高的精度。特别是相对于C4.5决策树算法，随机森林算法的特征随机选取过程和投票机制是一种改进和优化。

4.3 最优收入率选取算法有效性验证

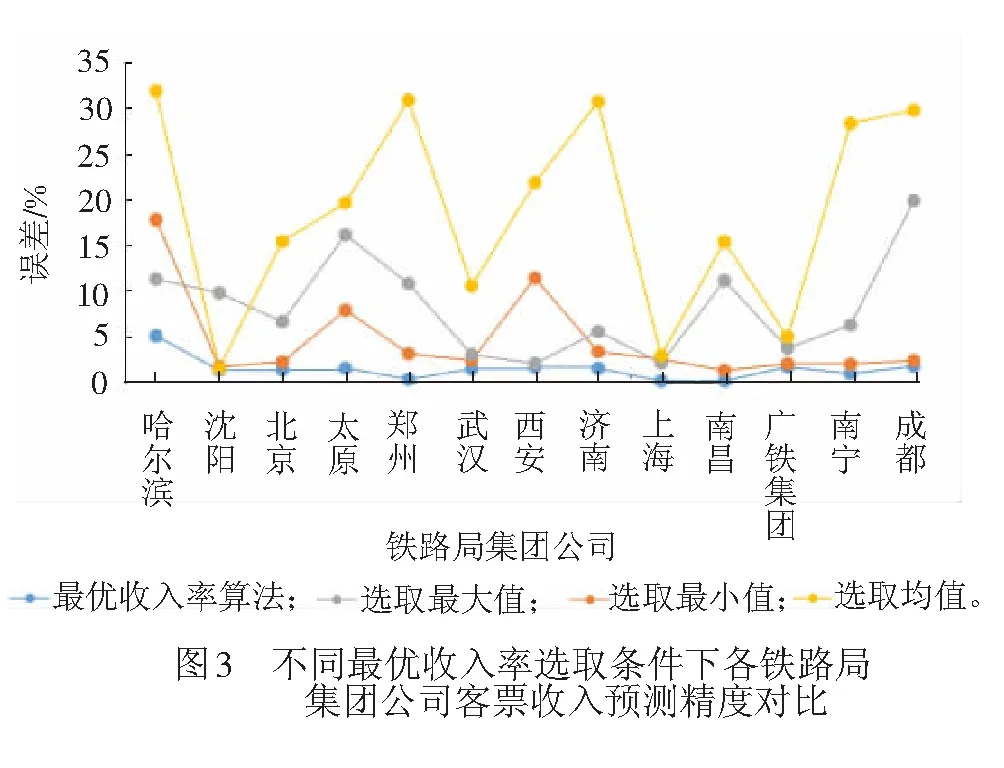
为了验证本文最优收入率选取算法的有效性，选取训练集中各个目标变量分类范围内的收入率最大值、最小值和均值分别作为最优收入率，并将利用它们计算的分站收入率和铁路局收入结果与本文的收入率计算结果进行对比，结果见表9。

表9 不同最优收入率选取预测结果精度对比

由表9和图3可知，本文提出的最优收入率选取方法可以较为准确地预测分站收入率和铁路局收入。特别是相比于传统的取均值的方法，本文提出的算法能够显著提高预测准确度。

5 结束语

本文通过对目标变量、因素变量的离散化处理，及分类后最优收入率选取的基础上，以收入率为目标对列车停靠站信息进行分类预测。从实验结果上看，本文中，改进、提出和采用的算法对于客票收入率分类和客票收入预测具有较高的操作性和有效性。此模型不仅能为管理部门提供一张清晰的决策表指导未来收入计划的下达。同时，这也能为运输部门高铁列车开行计划的制定起到一定的参考作用。随着12306旅客信息收集工作的逐步进行，在下一步的研究中，针对不同运输通道旅客出行行为[16]对列车分站收入进行更准确的预测。

参考文献：

[1] 刘春煌，王丽华，李聚宝，等.铁路运输企业收入清算系统总体方案的研究及旅客运输清算系统的实施[J].中国铁道科学，2003，24(1):12-18.

LIU Chunhuang，WANG Lihua，LI Jubao，et al. Researches on Overall Scheme of Revenue Clearing System for Railway Transportation Enterprises and Implementation on Passengers Transportation Clearing Sub-system[J].China Railway Science，2003，24(1):12-18.

[2] 汪学文，樊晓平.铁路客票收入清算复核系统的设计与实现[J].计算机与现代化，2007(6):120-122.

WANG Xuewen, FAN Xiaoping. Design and Implementation of Income Liquidation and Checking System for Railway Tickets[J].Computer and Modernization，2007(6):120-122.

[3] 王丽华，刘贺文，张晨阳，等.铁路旅客运输清算系统[J].铁路技术创新，2012(4):52-56.

WANG Lihua，LIU Hewen，ZHANG Chenyang，et al.Railway Passenger Transport Clearing System[J].Railway Technical Innovation，2012(4):52-56.

[4] 赵弇南.铁路客运清算系统的现状、完善与发展[D].北京：北京交通大学，2005.

[5] 李岱安, 方圆, 李静华,等.中国铁路旅客运输清算系统的研究与实施[C]//北京：中国铁道学会铁道信息化建设青年科技研讨会暨中国铁道学会青年学术会议.北京：中国铁道学会，2003.

[6] 史森林.铁路客票收入影响因素分析[J].铁道运输与经济，2004，26(8):37-40.

SHI Senlin. Analysis upon the Affecting Factors for Railway Ticket Income[J].Railway Transport and Economy，2004，26(8):37-40.

[7] 史森林.对铁路客票收入弹性预算原理的研究[J].中国铁路，2004(5):60-62.

SHI Senlin. Study on the Principle of Flexible Budget of Railway Passenger Ticket Income.[J].Chinese Railway，2004(5):60-62.

[8] 方伟.铁路局营业收入预测方法研究[J].产业与科技论坛，2012，11(7):110-111.

FANG Wei. Research on the Forecasting Method of Railway Administration Revenue[J].Industrial & Science Tribune，2012，11(7):110-111.

[9] 张钰莎，蒋盛益.连续属性离散化算法研究综述[J].计算机应用与软件，2014，31(8):6-8，140.

ZHANG Yusha，JIANG Shengyi. Survey on Continuous Feature Dicretisation Algorithm[J].Computer Applications and Software，2014，31(8):6-8，140.

[10] TSAI C J，LEE C I，YANG W P. A Discretization Algorithm Based on Class-Attribute Contingency Coefficient[J]. Information Sciences，2008，178(3):714-731.

[11] LUKASIK S，KOWALSKI P A，CHARYTANOWICZ M，et al. Clustering Using Flower Pollination Algorithm and Calinski-Harabasz Index[C]//Evolutionary Computation. New York：IEEE，2016，24-29.

[12] BREIMAN L. Random Forests[J].Machine Learning，2001，45(1):5-32.

[13] QUINLAN J R. C4.5: Programs for Machine Learning[M].Boston：Morgan Kaufmann Publishers，1993，71-80.

[14] 方匡南，吴见彬，朱建平，等.随机森林方法研究综述[J].统计与信息论坛，2011，26(3):32-38.

FANG Kuangnan，WU Jianbin，ZHU Jianping，et al.A Review of Technologies on Random Forests[J].Statistics & Information Forum，2011，26(3):32-38.

[15] LANDIS J R，KOCH G G. The Measurement of Observer Agreement for Categorical Data[J]. Biometrics，1977，33(1):159-174.

[16] 叶玉玲，王艺诗.沪杭运输通道内旅客出行方式选择行为研究[J].铁道学报，2010，32(4):13-17.

YE Yuling，WANG Yishi.Research on Travel Model Choice Behavior in Shanghai-Hangzhou Transport Corridor[J].Journal of the China Railway Society，2010，32(4):13-17.