高速铁路与航空中长途竞争的博弈分析

齐 鹤(中国铁路总公司 办公厅，北京 100844)

近年来，我国高速铁路发展势头迅猛。2016年7月国务院批复《中长期铁路网规划》，提出了“八纵八横”高速铁路主通道，同时规划布局高速铁路区域连接线，并发展城际客运铁路。高速铁路的发展极大地影响着我国居民出行方式的选择。然而在中长途客运市场上,作为高速铁路的主要竞争对象，航空客运在运营上更加灵活，如航空公司机票打折、歧视定价策略以及降低燃油税等措施,直接或间接导致了高速铁路上座率比较低,造成盈利不足,使得便捷、快速、高效的高速铁路不能有效服务大众,带动社会经济的发展。因而，在兼顾高速铁路特性的基础上，对高速铁路和航空运输的竞争进行深入分析有助于高速铁路运营策略的制定和社会资源的优化配置。

对于铁路定价以及与航空运输的竞争关系，许多学者进行了研究。史峰等[1]采用马氏纯灭过程描述了我国铁路动态票价问题，根据动态规划Bellman最优化原理推导出了用于最优策略动态定价的递推公式。四兵锋等[2]研究了多种交通方式竞争条件下的铁路客票价格制定的最优策略，考虑在公路和民航价格不变的前提下，普快、特快和高速铁路的票价制定方法，提出了一个双层规划模型。陈建华等[3]分析了影响旅客出行广义费用的因素，提出了计算旅客广义出行费用的方法，利用Logit模型描述了旅客出行的选择行为，并以铁路运输部门的经济效益最大为目标确定合适的票价。卞长志等[4]使用Nested Logit 模型分析出行者交通方式选择行为，并以价格为竞争策略变量建立了城际铁路和长途客运之间的完全信息静态博弈模型。蒋金亮[5]构建了高速铁路和民航的票价非合作博弈模型，讨论了票价对客运量、收益的影响。张迦南等[6]构建了双层博弈模型研究区域客运通道市场均衡状态的预测方法。栾维新等[7]研究了高速铁路与航空客运动态定价，考虑了票价变化对客流量变化的影响，建立了高速铁路与航空运输定价的斯坦科尔伯格博弈模型。Yang[8]等研究了高速铁路和航空运输博弈对定价、收益和社会的影响，以价格和发车频率为决策变量建立了高速铁路与航空运输的Bertrand博弈模型。张睿等[9]建立了高速铁路与航空运输定价博弈的双层规划模型，上层问题为高速铁路和航空定价的纳什博弈，下层问题为客户广义出行费用最小的出行者选择行为问题，并对北京到南京段高速铁路与民航的定价进行了分析。

已有的研究很少考虑高速铁路的公共服务职能，由于铁路的社会服务特性，在考虑运营成本收益时其定价策略需要兼顾社会民众满意度和承受能力；同时由于出行者特性的内在差异，对交通方式、票价、出行时间和出行便利性等具有不同的偏好，尽管列车高开行频率能提高出行者的出行便利性，却也同时增加了投资和运营成本，因此铁路在制定票价和列车开行频率等运营策略时对出行者进行细分能更好的反应旅客运输市场。针对这些问题，本文在建立高速铁路与航空运输竞争模型中考虑了反应社会民众满意度的消费者剩余，同时考虑了出行者时间价值差异的市场细分。

1 出行者交通方式选择因素分析

在客运市场中，影响旅客选择出行方式的因素主要为：经济性、速度性、便捷性、舒适性以及安全性。由于高速铁路和航空运输均为安全性很高的运输方式，为简化研究，本文假设出行者对两种客运方式安全性评估一致。出行者一般都倾向于旅行时间短、客票价格低并且舒适性高的运输方式，然而不同的出行者对不同运输属性的偏向不同。

1.1 经济性

出行者选择出行方式的总成本可以分为：接驳成本和其他成本，接驳成本包括从出发地到出发站成本、运输方式票价成本以及到达站到目的地成本，其他成本如餐饮等费用，是对出行者经济成本的总体现。因此，出行者选择交通方式i的总经济成本为

( 1 )

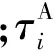
1.2 时间成本

考虑单一起讫点之间高速铁路和航空运输的竞争问题。已有研究表明出行者选择交通方式最主要考虑的因素为票价和总的出行时间[10-11]。对于交通方式i，出行者总的旅行时间包括接驳时间、在途时间和计划延迟[8]为

ti=ai+li/si+Ti/4fii=r,a

( 2 )

式中：ai为运输方式i的接驳时间；li、si分别为交通方式i的运行距离和平均速度；li/si为交通方式i的在途时间；Ti为运营时间；fi为服务频率；Ti/4fi为期望延迟时间[8,12-13]。

在客运市场上，不同出行者对旅行时间价值评价不同，从而支付意愿有差别。通过引入基于时间价值的旅客细分，出行者类型k的时间成本为

TTik=vktii=r,a

( 3 )

式中：TTik为出行者类型k选择交通方式i的时间成本，在一定程度上也反应了出行者对便捷性的要求；vk为出行者类型k的时间价值。

1.3 舒适性

出行者考虑出行时的另一个重要因素是舒适度。高速铁路和航空运输作为服务行业，其舒适度对于出行者的出行会产生较大的影响。对于运输服务行业，影响舒适度的因素包括：人均坐卧面积，旅途的时间，旅行过程中的环境，旅途中得到的服务质量等。现有的研究中，对舒适度的量化方式为出行者经过旅途后恢复体力的时间长短，基本假设为舒适度与恢复体力时间成负相关，舒适度好恢复体力时间短，舒适度差恢复体力时间长。出行者完成旅途后其疲劳恢复时间为[14]

( 4 )

( 5 )

因此，我们可以定义出行者类型k选择交通方式i的广义出行成本为Gik为

Gik=TPi+TTik+TRiki=r,a

( 6 )

2 交通方式成本收益分析和客运分担模型

2.1 交通方式成本与收益

根据经济学理论，交通运营商的利润由收入减去成本组成(假设不考虑税收因素)，其运营成本包括固定成本和单位可变成本[8]，可以表示为Ki+ciζi，其中Ki为固定成本，ci和ζi分别为交通方式i单位座位可变成本和乘客容量。交通方式i的收入主要为客票收入，表示为qiτili。因此，交通运营商的利润为

πi=qiτili-fi(Ki+ciζi)i=r,a

( 7 )

式中：qi为交通方式i的客运量。

2.2 客运分担模型

作为理性人，出行者一般基于最小化广义出行成本选择出行方式，然而实际中由于研究者一些观测不到或无法测量的因素(如出行者偏好或者车辆拥挤等)，出行者并不是总是选择广义出行成本最小的交通方式。因此，我们通过随机效用刻画出行者选择行为，认为乘客k选择交通方式i的效用Uik可以被分为两个部分，一部分是与可观测因素相关的效用确定项Gik，另一部分是与不可观测因素相关的效用随机项ei[15],则Uik为

Uik=-Gik+eii=r,a

( 8 )

假设随机项服从均值为0方差为π2/6θ2的Gumbel分布(双指数分布)，并且相互独立。根据随机效用最大化理论[16]，交通方式i的客运分担率可以表示为

i=r,a

( 9 )

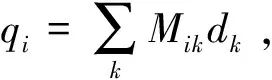
2.3 消费者剩余模型

由于高速铁路的社会服务特性，其在制定其票价和服务频率时需要考虑社会大众的承受能力。因此，我们采用消费者剩余来描述旅客采用高速铁路出行时的满意程度，由2.2节可知，旅客选择交通方式i出行的概率由式( 9 )描述，现在考虑交通方式i增加τ单位票价后，概率变为

i=r,aj=r,a

(10)

经过整理后

(11)

从式(11)中，可以看出当增加τ直到选择交通方式i出行概率为0时，可以获得单位收益的总增量可以表述为

i=r,a

(12)

根据文献[17]，经过积分后

(13)

旅客采用交通方式i出行的消费者剩余为

i=r,a

(14)

3 纳什博弈模型

在客运市场中，假定高速铁路和航空客运运营商之间进行的是非合作静态纳什博弈，即运营商之间同时选择运营策略或相互之间并不知道对方选择的运营策略。在纳什均衡状态下，一方运营商的运营策略是对另一方运营商运营策略的最优反应，交通方式运营者不会单方面改变运营策略。

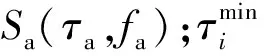
因而，高速铁路最大化利润和消费者剩余权重函数模型为

maxzr(Sr|Sa)=max(θ·CSr+πr)=

(15)

s.t.

(16)

(17)

fr∈{1,2,…,nr}

(18)

式(15)最大化了高速铁路利润和出行者消费者剩余，0≤θ≤1为消费者剩余权重系数。式(16)确保运送旅客量不超过高速铁路运送能力，其中运输能力通过交通运输需求量与分担率相乘得到。式(17)、式(18)分别定义了票价取值的上下限和服务频率的取值范围。

同样，航空运输最大化利润模型为

maxπa(Sa|Sr)=

(19)

s.t.

(20)

(21)

fa∈{1,2,…,na}

(22)

式(19)最大化了航空运输的利润。式(20)确保航空运送旅客量不超过其运送能力。式(21)定义了航空客票的上限和下限。式(22)定义了航空运输的服务频率。

4 纳什均衡求解

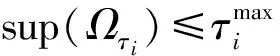
根据纳什均衡存在性定理[18]，一个有限博弈至少存在一个纳什均衡(纯策略或者混合策略)。然而在不允许混合策略均衡情况下，许多博弈问题可能并不存在纯策略纳什均衡。高速铁路和航空运输市场竞争博弈问题中，求解纯策略纳什均衡更具有实用性。然而，由于纯策略纳什均衡可能不存在，定义ξ近似纳什均衡如下[19-20]。

当ξ=0时，ξ为近似纳什均衡等价于纳什均衡。在求解时，只需考虑求解最小ξ对应的均衡，当minξ>0时，说明纯策略纳什均衡不存在。根据定义2，我们首先需要计算高速铁路和航空运输的收益矩阵，找到最小ξ对应的策略。步骤为：

Step1列出所有离散策略集：(Sr(·),Sa(·))，根据式( 9 )计算高速铁路和航空客运的出行者分担，根据如下函数计算高速铁路和航空客运的收益函数

(23)

(24)

式中：M为正无穷大。

Step2对于任意给定的策略组合(Sr(·),Sa(·))，确定占优策略，计算占优策略与给定策略组合的差距(ξr,ξa)。最后确定得到最小的ξ以及对应的高速铁路和航空运输策略。

5 案例分析

本文以北京至上海高速铁路与航空竞争作为分析例子。表1给出了案例分析中的模型计算参数。一般对于相同的起讫点，由于地理因素的影响，高速铁路的运输距离大于航空运输的距离。北京到上海的飞行距离是la=1 160 km，北京到上海高速铁路线路长lr=1 458 km。一般来说，航空运输航站楼设置在距市区较远地方，因而航空运输接驳时间大于高速铁路的接驳时间，虽然不同线路的接驳时间有所不同，典型的取值例子为ar=1 h，aa=3 h[8]；对于接驳费用，采用公共交通方式从市区到机场、车站或机场、车站到市区的费用，因此不失一般性的相应取值见表1。

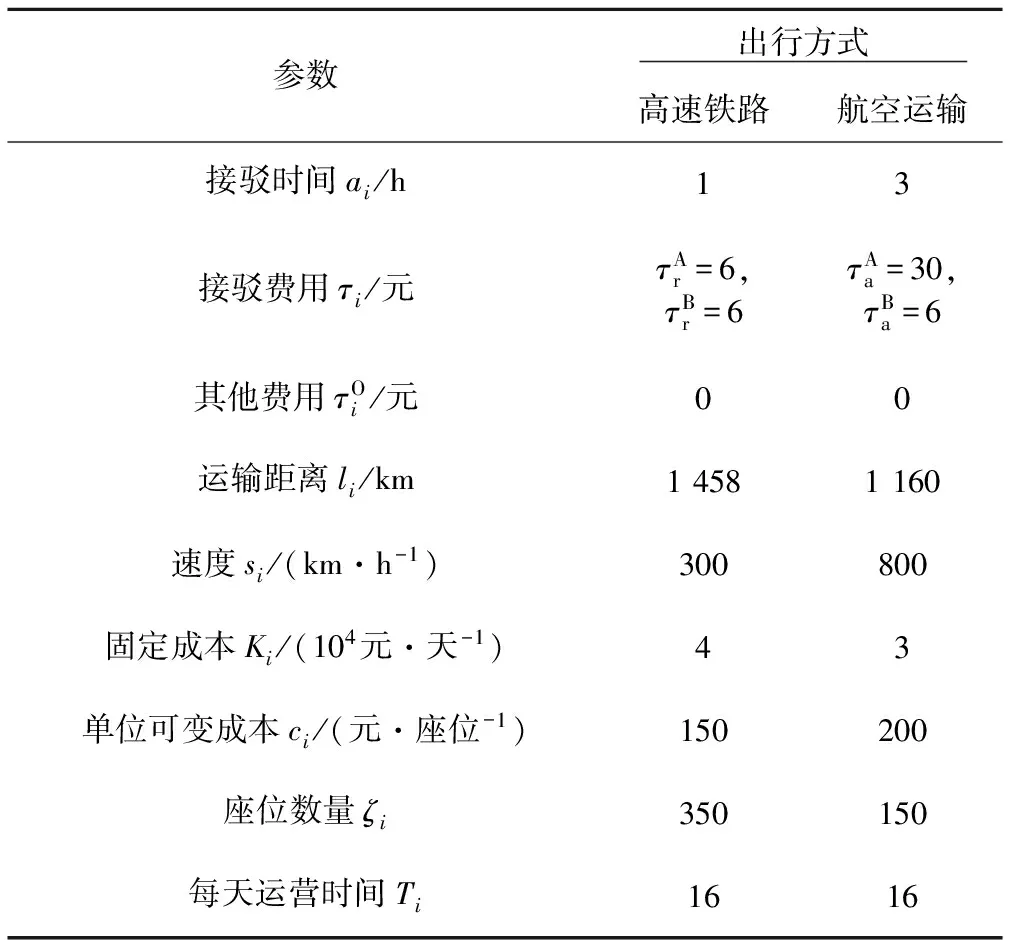
表1 模型中参数取值

客运机型不同巡航速度有差别，但速度一般相对稳定于800 km/h左右。根据中国铁路总公司数据，北京至上海高速铁路运行速度范围在250～350 km/h，不失一般性的，本例中高速铁路速度取值300 km/h。案例分析中出行者被粗略的分为：休闲旅客和商务旅客。根据国家统计局的数据，国内大城市人均GDP在30元/h左右，取其为休闲旅客的时间价值，而商务旅客的时间价值相对休闲旅客高出许多，取为90元/h[8]。

航空运输和高速铁路的固定成本和单位可变成本无法获取，我们参考文献[8]进行取值。高速铁路和航空运输的运营时间可以从中国铁路总公司网站和中国民航管理网站查询获得。每天高速铁路和航空最早出发时间在6:00 am左右，最晚出发时间在10:00 pm左右，因此运营时间大概为16 h。案例中，我们假设每天从北京到上海有30 000人客运需求。

根据出行者商务旅客比率的不同和目标函数中消费者剩余权重的不同(例如β=0.2,0.4,0.6，以及θ=0,0.3,0.6,1.0；β为商务旅客比率，θ为目标函数式(15)中的权重系数)，我们求解了12种不同情况下的博弈模型。其中，高速铁路票价取值范围τr∈[0,1.5]，离散数量mr=150，服务频率1≤fr≤100，nr=100；航空运输票价取值范围τa∈[0,2.0]，离散数量ma=200，服务频率1≤fa≤150，na=150。

5.1 均衡结果分析

表2给出了不同情况下高速铁路与航空运输竞争的ξ近似纳什均衡结果。从中我们可以看出随着高速铁路对社会福利的权重的增加，高速铁路和航空运输的利润均会下降，竞争双方均衡策略变化趋势：(1)高速铁路为均衡票价降低，而列车开行频率增加；(2)航空运输为均衡票价降低，客运飞机开行频率降低。这是由于高速铁路以最大化消费者剩余和利润为目标，增加服务频率可以减小预期等待时间从而增加消费者满意度，而航空运输只关注利润，减小服务频率可以降低成本。

当商务旅客比率增加时，高速铁路和航空运输均衡策略变化趋势：(1)高速铁路为均衡票价增加，列车开行频率有所降低；(2)航空运输为均衡票价增加，客运飞机开行频率增加。此外，商务旅客比率增加时高速铁路和航空运输均衡利润均增加，并且出行者采用高速铁路或航空运输的消费者剩余均增加，这是由于商务旅客的交通需求弹性较休闲旅客的交通需求价格弹性小，在票价的微小变动下出行需求变化较小。

综上分析，针对高速铁路票价制定策略和列车开行频率有如下建议：(1)对出行者满意度的权重宜设置在[0.3,0.6]之间，过低的权重会大大减少旅客满意度，而过高的权重会使得高速铁路经营入不敷出；(2)对客运市场进行细分，把握不同时期的客运市场旅客组成变化，在均衡票价制定和列车开行频率上做到更好的市场定位，做到民众满意和运营成本收益平衡；(3)客运市场以商务旅客为主导时，高速铁路可以适当提高票价，不仅可以增加利润而且也不降低出行者的满意度。

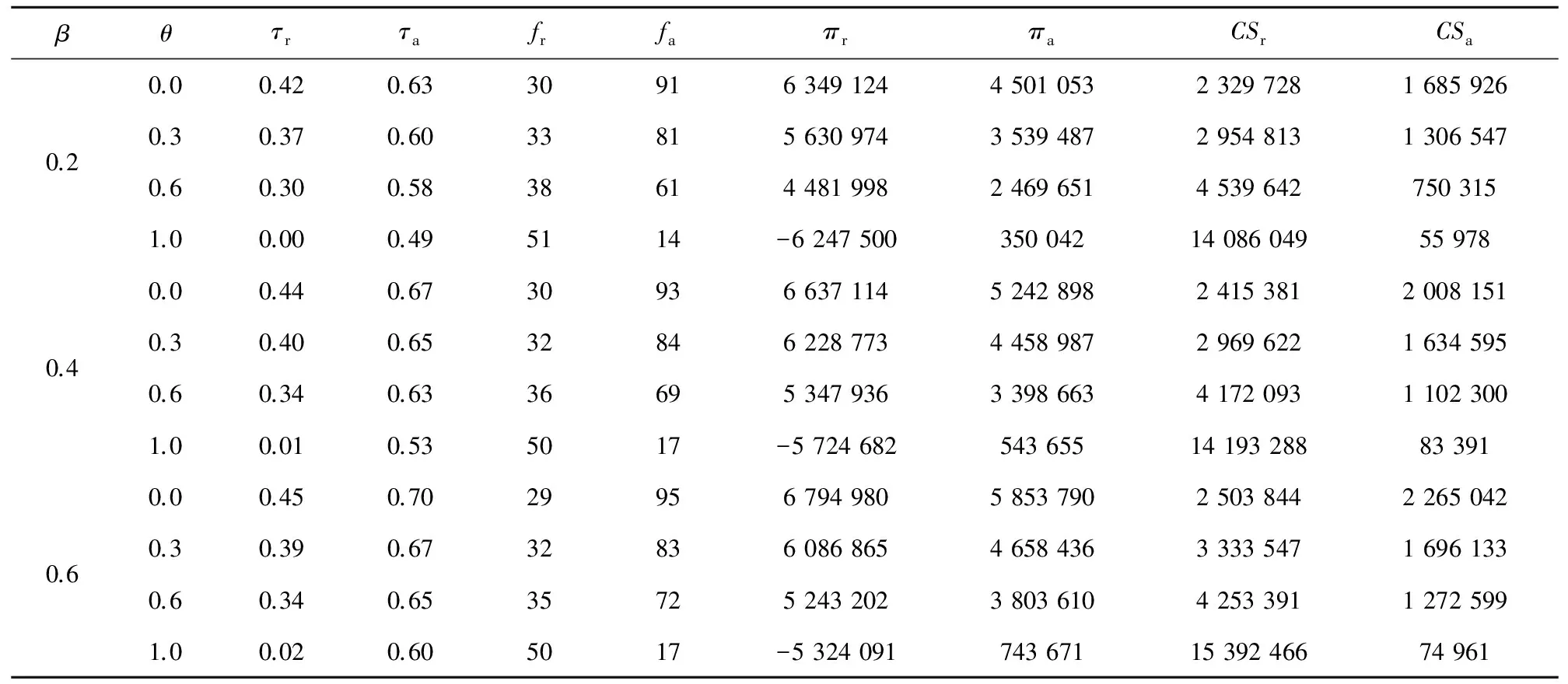
表2 高速铁路与航空运输竞争下的ξ纳什均衡结果

注：β为商务旅客比率；θ为社会福利权重；τr、τa分别为高速铁路单位票价和航空客运单位票价；fr、fa分别为高速铁路服务频率和航空运输服务频率；πr、πa分别为高速铁路利润和航空客运利润；CSr为乘坐高速铁路的消费者剩余；CSa为乘坐高速铁路的消费者剩余。

6 总结

本文研究了中长途单一起讫点之间高速铁路和航空客运之间竞争的问题，引入了消费者剩余的计算和基于时间价值不同的客户细分，建立了高速铁路和航空运输竞争下的博弈模型，模型中高速铁路在制定票价和列车开行频率策略时以最大化消费者剩余和利润的权重函数为目标，航空运输由于其完全的市场化以最大化利润为目标。

模型采用离散化方式进行求解，以北京到上海高速铁路和航空运输的竞争作为算例，分析了消费者满意度、出行者细分与均衡运营定价策略以及交通方式开行频率的关系。计算结果表明随着高速铁路对社会大众满意度的权重增加，高速铁路和航空运输的利润均会下降，结果与文献[8]中的分析一致。同时，当高时间价值旅客出行比率增加时，高速铁路适当提高票价不仅能提高利润而且不减少旅客出行满意度，因此当客运市场以高时间价值旅客为主导时，高速铁路宜适当提高票价；此外，高速铁路在票价制定和列车开行频率策略时，对模型中消费者剩余的权重系数宜设置在[0.3,0.6]之间，以平衡出行者满意度和高速铁路经营成本收益。

本文研究未考虑航空运输针对不同出行者的歧视定价策略，也并未细致区分不同等级座位的票价制定，而铁路在履行公共服务职能的时候可以更加灵活，高速铁路定价既要照顾到必要的成本开支，也要考虑到多数社会公众的承受能力。如二等座应满足多数人的需求，而一等座、商务座则可在多元化服务上下功夫。

参考文献：

[1] 史峰，郑国华，谷强. 铁路客票最优动态票价理论研究[J]. 铁道学报，2002，24(1):1-4.

SHI Feng，ZHENG Guohua，GU Qiang.Optimal Dynamic Pricing of Railway Passenger Ticket[J].Journal of the China Railway Society，2002，24(1):1-4.

[2] 四兵锋，高自友. 合理制定铁路客票价格的优化模型及算法[J]. 管理科学学报，2001，4(2):45-51.

SI Bingfeng，GAO Ziyou.Optimal Model and Solution Algorithm for Railway Passenger-ticket Pricing[J].Journal of Management Sciences in China，2001，4(2):45-51.

[3] 陈建华，高自友. 合理制定铁路旅客票价的优化方法[J]. 铁道学报，2005，27(4):16-19.

CHEN Jianhua，GAO Ziyou.Optimal Railway Passenger-ticket Pricing[J].Journal of the China Railway Society，2005，27(4):16-19.

[4] 卞长志，陆化普，尉欣欣. 城际铁路和公路长途客运的定价博弈[J]. 交通运输系统工程与信息，2010，10(1):184-189.

BIAN Changzhi，LU Huapu，YU Xinxin. Price Game between Intercity Railway and Bus[J].Journal of Transportation Systems Engineering and Information Technology，2010，10(1):184-189.

[5] 蒋金亮. 基于非合作博弈的高速铁路票价优化研究[D]. 北京：北京交通大学，2012.

[6] 张迦南，赵鹏. 基于博弈论的区域客运通道市场均衡研究[J]. 铁道学报，2012，34(5):1-8.

ZHANG Jianan，ZHAO Peng.Research on Market Equilibrium of Regional Passenger Transport Corridors Based on Game Theory[J].Journal of the China Railway Society，2012，34(5):1-8.

[7] 栾维新，张旭，赵冰茹，等. 诱发客流影响下高速铁路及航空运输客票动态定价研究[J]. 铁道运输与经济，2012，34(7):8-13.

LUAN Weixin，ZHANG Xu，ZHAO Bingru，et al. Research on Dynamic Ticket Pricing of High-speed Railway and Air Transportation under Influence of Induced Passenger Flow[J].Railway Transport and Economy，2012，34(7):8-13.

[8] YANG H，ZHANG A. Effects of High-speed Rail and Air Transport Competition on Prices，Profits and Welfare[J]. Transportation Research Part B :Methodological，2012，46(10):1322-1333.

[9] 张睿，栾维新，赵冰茹. 基于旅客选择影响的高速铁路及航空客票定价博弈分析[J]. 铁道运输与经济， 2015，37(1):5-9.

ZHANG Rui，LUAN Weixin，ZHAO Bingru. Game Analysis on Ticket Pricing of High-speed Railway and Civil Aviation Based on Influence of Passenger Selection[J].Railway Transport and Economy，2015，37(1):5-9.

[10] BEHRENS C，PELS E. Inter Modal Competition in the London-Paris Passenger Market: High-speed Rail and Air Transport[J]. Journal of Urban Economics，2012，71(3):278-288.

[11] D’ALFONSO T，JIANG C，BRACAGLIA V. Would Competition between Air Transport and High-speed Rail Benefit Environment and Social Welfare?[J]. Transportation Research Part B: Methodological，2015，74:118-137.

[12] BRUECKNER J K. Network Structure and Airline Scheduling[J]. Journal of Industrial Economics，2004，52(2):291-312.

[13] BRUECKNER J K，FLORES-FILLOL R. Airline Schedule Competition[J]. Review of Industrial Organization，2007，30(3):161-177.

[14] 张田. 航空竞争下我国高速铁路定价策略研究[D].重庆：重庆交通大学，2016.

[15] 吴世江，史其信，陆化普. 交通出行方式离散选择模型的效用随机项结构研究综述[J]. 公路工程，2007，32(6):92-97.

WU Shijiang，SHI Qixin，LU Huapu.Review of Error Structure Extension of Discrete Choice Models in Travel Model Choice[J].Highway Engineering，2007，32(6):92-97.

[16] BEN-AKIVA M，MOSHE E. Discrete Choice Analysis : Theory and Application to Travel Demand[M]. Massachusetts: MIT Press，1987.

[17] MCCONNELL K E. Consumer Surplus from Discrete Choice Models[J]. Journal of Environmental Economics & Management，1995，29(3):263-270.

[18] NASH J. Non-Cooperative Games[J]. Annals of Mathematics，1951，54(2):286-295.

[19] BOSSE H，BYRKA J，MARKAKIS E. New Algorithms for Approximate Nash Equilibria in Bimatrix Games[J]. Theoretical Computer Science，2007，411(1):164-173.

[20] WANG H，MENG Q，ZHANG X. Game-theoretical Models for Competition Analysis in a New Emerging Liner Container Shipping Market[J]. Transportation Research Part B:Methodological，2014，70:201-227.