基于阵元激励幅度分档的赋形波束方向图综合
杨垠,盛卫星,韩玉兵,马晓峰
南京理工大学 电子工程与光电技术学院,南京 210094
对阵列天线阵元激励幅度进行量化,将阵元激励幅度量化成固定数目的量化台阶,这就是阵元激励幅度分档问题。常用的幅度分档优化主要分为3种,一种是幅度锥化加权。经典的幅度锥化加权算法诸如泰勒分布加权、切比雪夫分布加权[1]等已然成熟,被广泛应用于各种实际工程中。但是主瓣增宽、增益下降等缺点却大大限制了这些算法的进一步应用。在这些算法的基础上各种改进幅度锥化加权算法相继被提出。文献[2]提出了部分幅度锥化加权算法,只对阵列最外围的N个阵元加以幅度锥化加权,对于其他的阵元在均匀分布加权的基础上,加上一个切比雪夫多项式,来起到降低副瓣的作用,这样在近似达到完整幅度锥化加权的同时,也能弱化其所带来的缺陷。文献[3]提出了基于测试天线增益和副瓣的幅度锥化加权,使用了单参数泰勒线源分布和单参数汉森圆分布来作为口径分布,然后通过控制其中的参数来调整主瓣宽度、副瓣电平和增益大小之间的关系。幅度锥化加权还被应用到了大型阵列中。文献[4]给出了两种关于对子阵使用幅度锥化加权的方法,同时文献[5]将传统的子阵幅度锥化加权和遗传算法相结合,这样无论线阵和圆阵都可以得到优化。
尽管各式各样的技术被相继提出以提升幅度锥化加权的性能,但是其低增益宽主瓣的固有缺陷却只能被削弱而无法被消除。为了弥补其不足,密度锥化加权算法被引入。密度锥化加权算法大致分为两种,一种是通过对阵元摆放位置不断的试验,以使其能准确地和理想地幅度锥度分布匹配;或是根据某种逼近技术对整个口径分布的积分做逼近,以得到一组阵元的空间密度分布[6-10]。这种方法属于早期的密度锥化加权算法,通过实验或是以口径分布作为逼近准则使得它们不能提供很准确的数据。另一种方法是一种数值方法[11],它使用理想幅度分布作为一个概率密度函数,用这个函数来决定某个阵元是否将坐落于口径上的固定位置。文献[12]将密度加权阵与遗传算法相结合,使用非线性算法对密度阵进行了优化。
密度锥化加权阵相比幅度锥化加权阵来说在控制方向图副瓣性能方面略有不足,同时这类算法是将阵元位置作为变量来进行加权,这在许多阵元位置固定的天线上无法适用。因此,多阶密度加权阵的概念开始流行。文献[13-15]在密度加权的基础上提出了阵元激励幅度分层的概念,即对加载在每个阵元上的激励幅度分为了几个档位,这样在一定程度上弥补了密度加权阵副瓣降低的不足。文献[16]提出了一种固态阵列天线副瓣控制的方法。对于一个平面矩阵阵列,用一个平面椭圆阵列来逼近,将整个口径按照长短轴比分为相应的N个区域,每个区域内的阵元激励幅度都是相同的,然后通过梯度搜索的方法来得到相应区域的划分以及阵元激励的选取。不过,由于使用椭圆口径来逼近,口径面积利用率被大大减少。文献[17-19]通过概率统计的方法,事先设计出一组处于0和1之间的数,然后根据概率理论将这组权重和理想的阵元激励进行逼近,从而得到这组量化数值。同时期,文献[20-21]提出了一种直接优化量化综合(DOQSM)的方法,将对方向图指向性的要求变为了对主瓣宽度的最小化,并作为其目标函数;在限制方面,除了对副瓣的控制之外,还加入了对量化台阶的限制,使得优化结果更具实际性。在近年来,多阶密度加权阵开始和非线性优化算法相结合,文献[22-23]中分别介绍了多阶加权密度阵和变异退火遗传算法(AMAGA)以及粒子群算法相结合的应用。
本文提出了一种新的基于幅度分档的方向图综合方法。该方法首先利用交替投影得到综合方向图的阵元激励,然后使用概率密度分布理论对阵元激励幅度进行量化,最后在量化阵元激励幅度的基础上通过半正定松弛(SDR)[24]方法得到阵元激励的相位分布。本文结构如下:第1节给出了综合方向图的表达式;第2节使用概率密度分布方法得到量化的阵元激励幅度;第3节详述了如何根据量化阵元激励幅度获取阵元激励相位的步骤,其中SDR方法的应用被重点介绍;第4节列出了算法的整体流程;第5节给出了仿真算例以及对算法性能的分析。
1 综合方向图
为了方便下文表述,本文使用uv坐标系来定义方向图空间,表示为
{u=sinθcosφ
v=sinθsinφ
(1)
式中:θ和φ为俯仰角和方位角。假设有N个阵元,排布在一个任意形状的阵列上,第n个阵元的坐标为(xn,yn),fn(u,v)为相应的嵌入式阵元方向图。根据文献[25]可得,阵列天线的远场辐射方向图为
(2)
式中:In为阵元激励为;ψ=2π/λ为波数,λ为波长。将综合方向图离散化,在整个uv平面上采样M个点得到(um,vm)|m=1,2,…,M,则综合方向图的矩阵表达式为
{[F]M×1=XI
[X]M×N=Fe⊙B
(3)
式中:Fe=[f1f2…fn…fN],I=[I1I2…In…IN]T,fn=[fn(u1v1)
fn(u2,v2) …fn(uM,vM)]T。符号⊙为矩阵之间的hadamard乘积。阵列导向矢量B代表了阵列的结构特性,其表达形式为
[B]M×N=[b1b2…bn…bN]
[bn]M×1=
根据上述参数表示,式(3)中的矩阵X可以表示为X=[β1β2…βn…βN],其中βn=fn⊙bn。
这里,嵌入式阵元方向图被定义为当阵列中一个辐射阵元被激励其他阵元接负载时的远场辐射方向图[26]。本文使用加权反向交替投影(Weighted Alternating Reverse Projection,WARP)算法[27]来获取波束的无激励幅度限制的阵元激励。文献[27]中已对该算法进行了详细分析,在这里不再赘述。
2 幅度量化
在第1节中,结合WARP算法和阵列方向图模型,得到了方向图的无激励幅度限制的阵元激励。本节将给出如何对得到的激励幅度加以优化使其达到量化的效果。
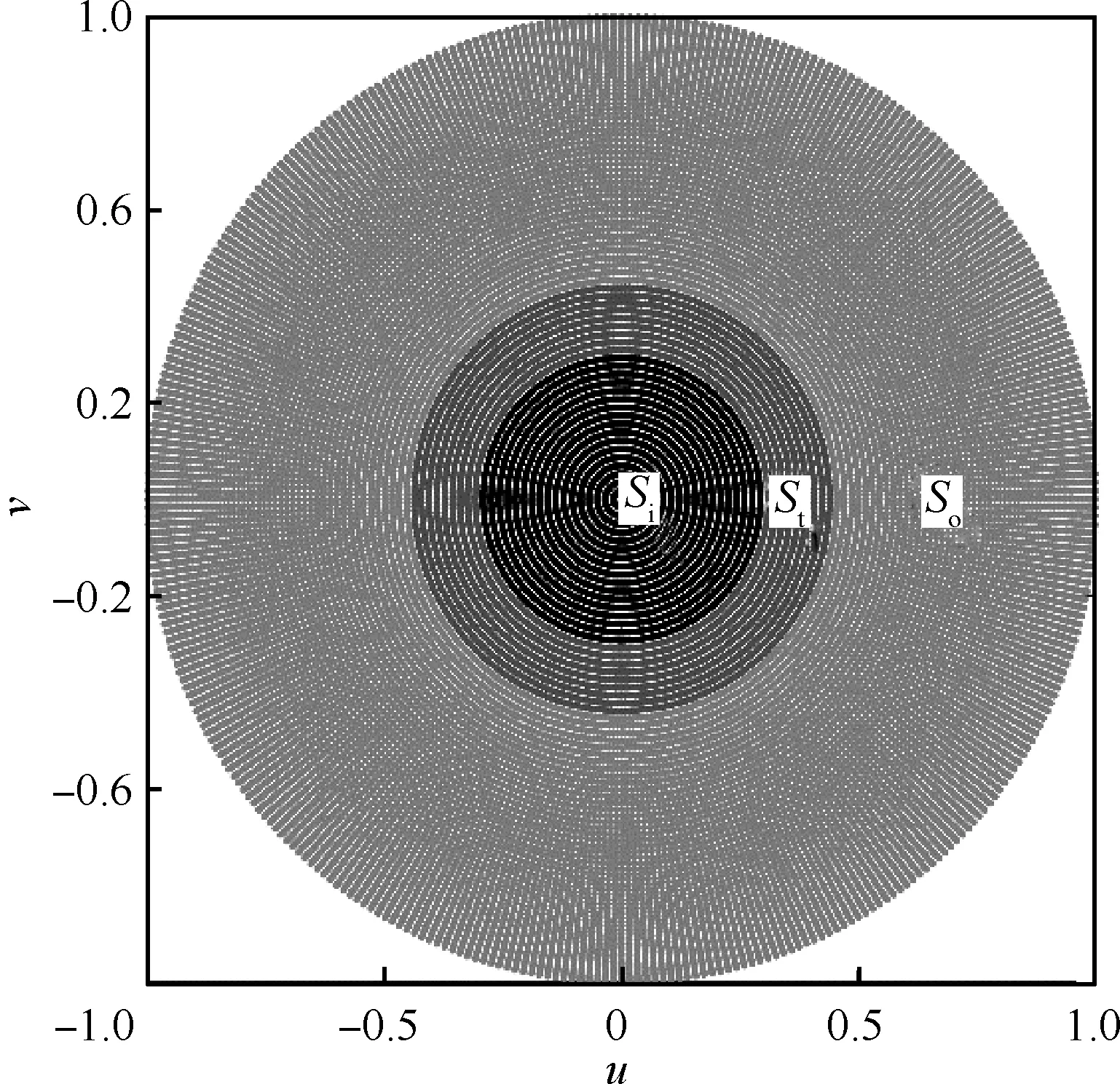
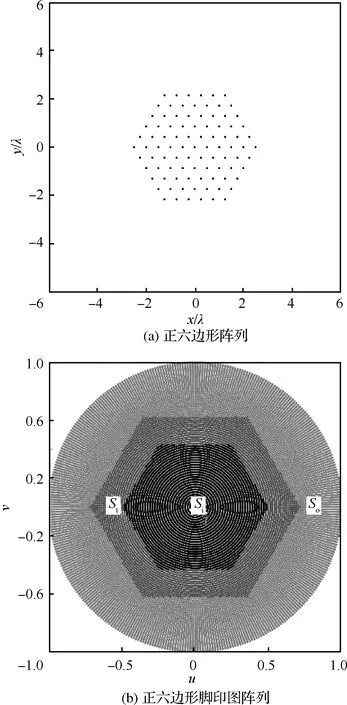
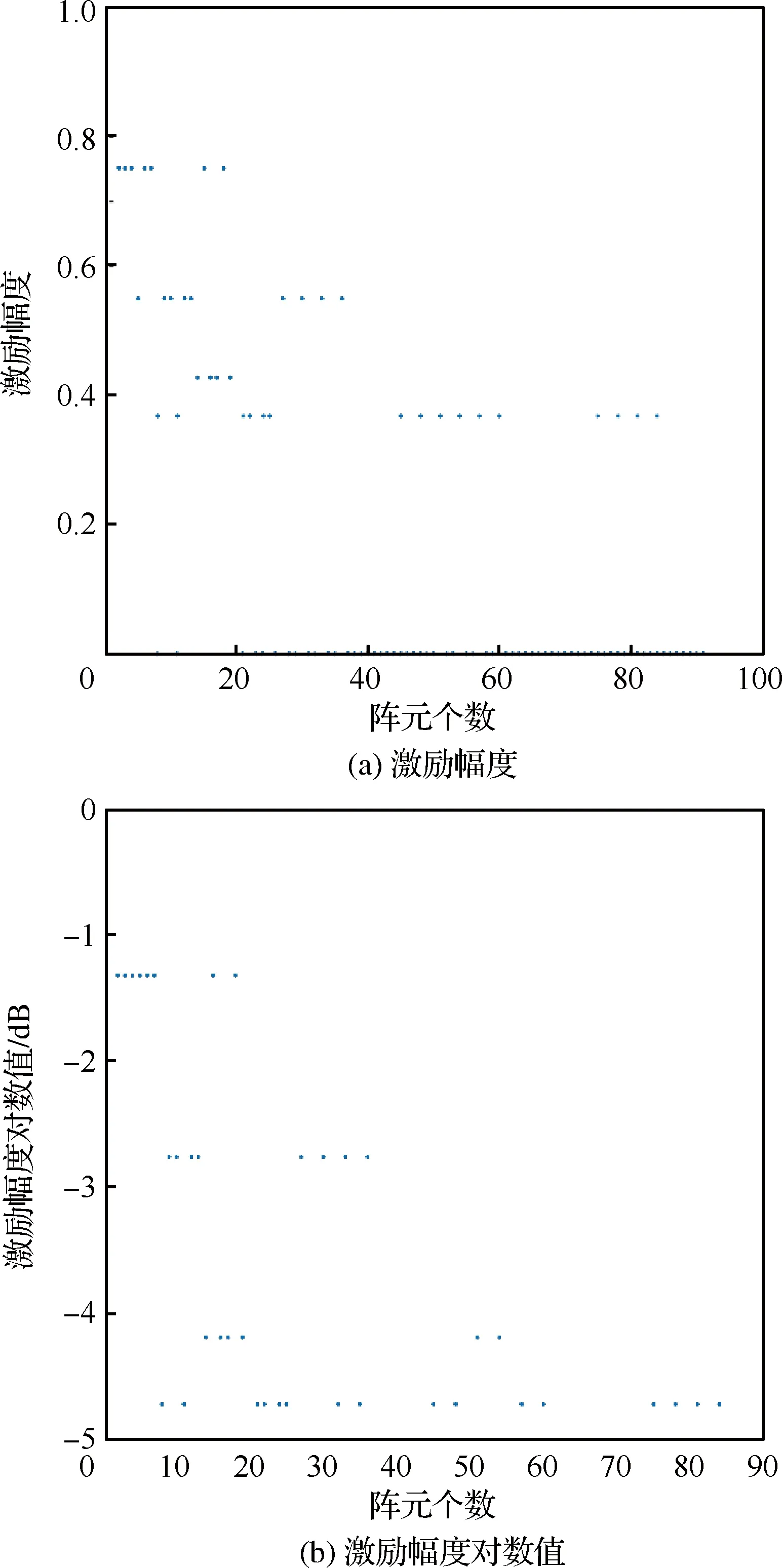
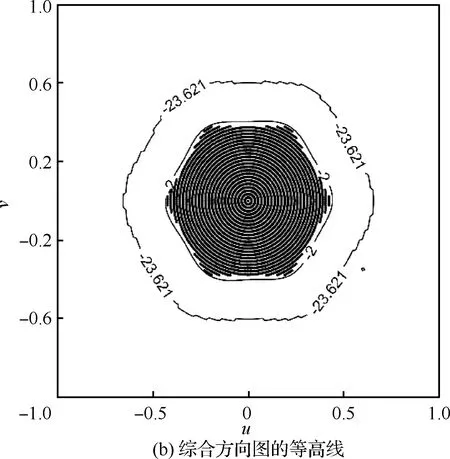
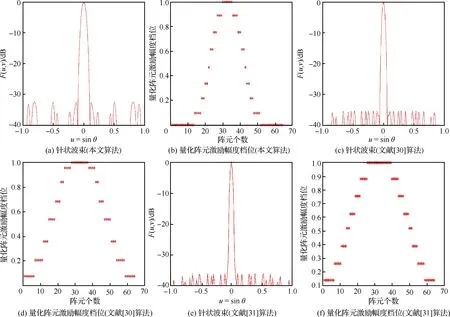
对式(2)中的阵元激励值幅度归一化,并用一组随机变量Ln来表示,这里Ln的取值为C0,C1,…,CK,(C0≡0,Ck-1 FL(um,vm)= (4) 式中:φ(n,um,vm)=φIn+φfn(um,vm),φIn为第n个阵元的激励相位,φfn(um,vm)为第n个阵元的阵元方向图在(um,vm)方向的相位。FL(um,vm)称之为随机变量方向图。将第1节中得到的阵元激励用Id表示,并且将使用Id得到的综合方向图称为理想方向图。则根据式(3),理想方向图Fd可表示为 [Fd]M×1=XId (5) 由于所有阵元激励所得到的方向图的平均值须等于理想方向图。结合式(5),该性质可用公式表示为 E[FL(um,vm)]=Fd(um,vm) (6) 式中:E[FL(um,vm)]为对随机变量方向图的每个采样点取均值;Fd(um,vm)为Fd中的第m个元素。从式(4)中可以看出,随机变量方向图中除了Ln中没有其他随机变量,因此式(6)可写为 E[FL(um,vm)]= (7) 结合式(6)和式(7)可得 (8) (9) 式中:pn为第n个阵元激励归一化幅度选取档位的概率。 这样E[Ln]=pnCk+(1-pn)Ck+1。结合式(8)和式(9),可得 (10) 从上述推导可以看出,量化台阶的选取标准为使量化的激励幅度综合出来的方向图的平均值尽可能的和理想方向图一致。然而仅凭此并不能使该方法具有实用价值。当得到的每个综合方向图都偏离理想方向图较远时,即使方向图的均值等于理想方向图也没有用,因为这个均值是不能被具体实现的,从而统计理论也失去了其实用价值。因此,在这里我们给出了方差的概念,即综合方向图和理想方向图之间的差距大小。方差可表示为 (11) 鉴于整个阵列方向图表达式中Ln是唯一的随机变量,结合式(7)可以将式(11)作如下变换: (12) (13) 式中: α(m,p,q)=ψum(xp-xq)+ψvm(yp-yq)+ [φ(p,um,vm)-φ(q,um,vm)] (14) 根据式(12)和式(13),式(11)可写为 cos(α(m,p,q))cov(Lp,Lq) (15) 式中:cov(Lp,Lq)为Lp和Lq的协方差。从式(9)可看出,所有随机变量之间相互独立,因此式(15)中的cov(Lp,Lq)=0。如此,式(15)可以写为 (16) 将式(10)代入式(16),可得 (17) 则式(11)可写为 (18) (19) 由于式(19)是一个非线性优化问题,因此可以用MATLAB中的fmincon函数来求解其最优解。 在求得量化电平之后,根据式(19)来选取这些量化电平的分布范围。当一个阵元的激励幅度落在[Ck,Ck+1]之间时,可以根据式(10)将相应的概率分布pn算出来。当pn≤1-pn时,激励幅度取Ck+1,当pn>1-pn时,激励幅度取Ck。这样,就得到了阵元激励幅度量化电平以及每个量化电平的分布位置。得到的量化阵元激励幅度用Ir表示,Ir为N×1维的列向量。 第2节中给出了量化阵元激励幅度的计算方法,本节将重点描述如何在该组激励幅度加载下获取波束的激励相位信息。图1为一个脚印图的示例,其中深灰色部分为赋形区域Si,So为非赋形区域。中灰色部分则代表了过渡区域St。 设方向图在赋形区域内的理想形状表达式为Gd(u,v)。为表征两个曲面相似程度,引入指标函数: (20) 图1 带有赋形区域、过渡区域、非赋形区域的脚印图Fig.1 Footprint with shaped region, transient region and unshaped region 除综合方向图在赋形区域的形状要求外,在非赋形区域的方向图能量应抑制得足够低以获得较低的副瓣区域电平。∬So‖F(u,v)‖2dudv可以表示非赋形区域的方向图能量。与此同时,赋形区域的方向图能量∬Si‖F(u,v)‖2dudv需要优化得尽可能高,这样整个系统的能量才能最大程度地被分配在主瓣波束内,而且在过渡区域的方向图也能有一个较快的下降速率。 考虑到上述优化项,优化方程可构建如下: (21) 式中:一共有两个正则化参数,分别为μ1和γ。其中μ1为表征副瓣电平和主瓣波动度之间关系的参数,通常根据过渡区域的大小来设定。 本文将其设定为非赋形区域和赋形区域的面积的比值。由于过渡区域在整个综合过程中起着相当重要的作用。扩大过渡区域会导致主瓣波动度的升高,而减小它则会引起副瓣电平的变坏。赋形区域和非赋形区域中的采样点离过渡区域越近,这种现象越明显。基于上述理论,由于设定为非赋形区域和赋形区域的面积的比值,因此当过渡区域扩大时,μ1相应降低,以此来补偿过渡区域对于综合方向图的影响。 第2个正则化参数γ的作用为平衡主瓣增益和副瓣电平之间的关系。在使用本文算法综合方向图之前,事先会确定综合方向图需要达到的最高副瓣电平以及主瓣增益,然后将γ设定为最高副瓣电平与主瓣增益的比值。这样,非赋形区域内方向图的积分和赋形区域内方向图的积分之间即可保持这恒定的关系,从而使得综合出来的方向图尽可能地达到先前设定的最高副瓣电平及主瓣增益的目标。 根据离散数值积分的概念,可将式(21)中的3个优化项写为 (22) (23) 式中:W1、W2和W3为3个对角矩阵,分别代表了式(22)中3个积分优化项里数值积分的矩阵形式。其形式如下 (24) 此外 (25) 其中: (26) 其中:Gd为Gd(u,v)的向量形式;./代表了两个矩阵中对应位置的元素相除。 假设向量Ip代表阵元激励的相位部分,则波束的阵元激励可表示为I=diag(Ir)Ip的形式。代入式(23)中,则可得 (27) 式中: (28) 根据文献[24],使用如下关系 ρHQρ=Tr(QρρH) (29) (30) 将式(30)代入式(25)中,可得 (31) 式中:Zi为一个N×N维的矩阵,其中的元素除了Zi(i,i)=1之外皆为0。由于对于Yp秩约束的存在,式(31)并不是一个凸优化问题。因此,将秩约束去掉后,式(31)即可转换成一个如下的凸优化问题 (32) 使用CVX工具箱[28]即可求得Yp。 求得Yp后,如何从中分解出合适的阵元激励相位便成了需要进一步解决的问题。传统的分解方法有3种:① 特征值分解法(文献[24]) ;② 降秩特征分解法(文献[29]);③ 随机分解法(文献[24])。 其中,随机分解法在三者中有最好的效果[24],因此本文选择随机分解法来获取阵元激励的相位信息。3种方法的分析和效果已在文献[24]中给出,因此本文不再赘述,这里直接给出相位获取步骤。 步骤1 设定一个随机变量个数D。 则Ip=δimin即为最终得到的相位解。 综上所述,本文提出的基于概率密度分布的量化阵元激励幅度方向图综合步骤如下: 步骤1 输入方向图的脚印图信息。 步骤2 设定Gd(u,v)和μ1。 步骤3 使用加权交替投影算法得到综合方向图的无阵元激励幅值限制的归一化阵元激励Id。 步骤4 对Id使用概率密度方法处理得到量化后的阵元激励幅值。 步骤5 通过式(25)和式(26)得到Q1、Q2和Q3。 步骤6 将Q1、Q2和Q3代入式(30)得到式(32),使用cvx工具箱求解式(32)得到Yp。 步骤7 使用随机法从Yp中提取出最优阵元激励相位Ip,并得到最终阵元激励I=diag(Ir)Ip,从而得到相应的赋形波束综合方向图。 本节通过3组算例对文中算法的性能进行了例证。第1组算例给出了平顶方向图的赋形效果,算例中使用的阵元方向图为嵌入式阵元方向图。算例使用的脚印图和阵列阵元排布形状较为规则,为一个正六边形的区域。算例给出了使用量化阵元激励幅度综合的方向图与非量化阵元激励幅度综合的方向图性能对比,以此来得出量化阵元激励幅度的效果。第2组算例为对赋形波束的方向图综合仿真,阵列的阵元方向图同样均为嵌入式阵元方向图。该算例主要意义在于检测文中算法对于非平顶方向图的赋形效果。第3组算例为一组对比算例,算例中给出了在阵列阵元个数相同,阵元激励法幅度量化的档位个数不同,以及阵列阵元个数不同,阵元激励法幅度量化的档位个数相同的两种情况下,综合方向图的效果,从而给出了量化档位对于综合方向图的影响。在这里,一些仿真参数设定如下: 1)ri=max{d(x)|x∈Si},rt=max{d(x)|x∈St},其中d(·)代表与原点的欧几里得距离。 2) 所有的综合方向图都为归一化方向图了。 3)M=91×181。 4) 所有阵元都是微波贴片天线。 5) 算例中的阵元激励幅度均为归一化阵元激励幅度。 6) 所有算例均是在2.6 GHz主频的笔记本电脑(Intel I5-4200M CPU 4 GB SDRAM)上进行的。 图2 阵列结构和脚印图Fig.2 Array structure and footprint 图3 归一化量化阵元激励幅度及其对数值Fig.3 Excitation amplitude and logarithmic value of normalized element array 图4 使用非量化幅度的阵元激励得到的综合 方向图及等高线 Fig.4 Synthesized pattern and its contour line with non-normalized element excitations amplitudes 本节给出了平顶方向图的综合算例。该算例使用的阵列在图2(a)中被给出,为一个由91个阵元组成的六边形阵列,阵元间距为半波长,同时脚印图为图2(b)中给出的六边形规则脚印图。赋形区域Si、过渡区域St和非赋形区域So在图中被标出,采样点数Min=9 931,Mext=17 924,ri=0.5,rt=0.72。图3(a)给出了阵元激励幅度的量化分档。共分6档,0、0.337 1、0.380 9、0.529 4、0.736 8和1。图3(b)为量化档位的对数值,可以看出量化后阵元激励的动态范围为4.7 dB,可以满足大部分的工程应用要求。综合结果在图4中被给出。其中图4(a)和图4(b)为使用普通阵元激励得到的综合方向图及其等高线图,图5(a)和图5(b)为使用幅度量化的阵元激励得到的综合方向图及其等高线图。从图4和图5中可看出,不论是使用量化幅度的阵元激励还是使用非量化幅度的阵元激励,综合方向图的赋形区域均被-3 dB等高线完全围住。其中,使用非幅度量化的阵元激励得到的综合方向图在主瓣区域内的波动度为2 dB,而使用量化幅度的阵元激励得到的综合方向图在主瓣内最大波动度为3 dB。与此同时,副瓣最高电平值分别为-23.62 dB和-20 dB。因此,幅度量化后的阵元激励综合出的方向图性能相比量化前并没有很大的衰退。此外,图4中的综合方向图在波束离开赋形区域后立刻开始下降,并且在赋形区域达到了-20 dB,这说明综合方向图能够满足脚印图的设定。算例中方向图的方向性系数为13.001。 图5 使用量化幅度的阵元激励得到的 综合方向图及等高线 Fig.5 Synthesized pattern and its contour line with normalized element excitations amplitudes 本节给出了使用幅度量化的阵元激励对赋形方向图的综合结果。图6(a)给出了综合方向图的脚印图和所用的阵列。波束的脚印图为一个长方形,Min=3 898,Mext=24 857,ri=0.316 2,rt=0.514 8。赋形波束顶部形状为 Gd(um,vm)=((um)2+(vm)2+0.2)|(um ,vm )∈Si (33) 图6(b)给出了赋形所用的阵列图。阵列为13×13的方阵,阵元间距半波长,每个阵元的阵元方向图为嵌入式阵元方向图。 图7和图8给出了赋形方向图的综合展示。其中,图7为使用非幅度量化的阵元激励综合的方向图赋形结果,图8为使用幅度量化的阵元激励综合的方向图赋形结果。两种情况下,波束的最大副瓣电平值均未超过-20 dB,同时赋形波束在赋形区域内的形状与理想方向图基本一致,最大差距不超过1 dB。此外,从图中可以看出,使用本文算法得到的赋形方向图在性能上与使用非量化幅度阵元激励得到的赋形方向图相差无几,这说明本文算法得到的量化幅度的阵元激励可以较好地完成赋形波束的方向图综合。图9给出了该组算例的阵元激励量化幅度分布图。阵元激励幅度的量化共分成了9个档位,分别是1、0.81、0.76、0.67、0.64、0.61、0.56、0.55和0。图9(a)给出了量化阵元激励幅度的分布,图9(b)为其对数取值。 图6 赋形波束脚印图及阵列Fig.6 Footprint of shaped-beam pattern and array structure 图7 非幅度量化阵元激励综合的长方形赋形波束Fig.7 Rectangular shaped-beam pattern synthesis with non-normalized element excitation amplitudes 图8 幅度量化阵元激励综合的长方形赋形波束Fig.8 Rectangular shaped-beam pattern synthesis with normalized element excitation amplitudes 图9 归一化量化阵元激励幅度及其对数值Fig.9 Normalized element excitation amplitudes and logarithm value of arrary 在方向图综合问题中,阵元激励的幅度个数作为变量的自由度对综合方向图的性能有着极大的影响,因此本节给出了阵元激励幅度量化档位个数对于综合方向图的影响。赋形算例为使用图2(a)中的正六边形阵列来完成一个脚印图为正方形的平顶方向图。脚印图如图10所示,其中Min=6 063,Mext=23 039,ri=0.282 9,rt=0.565 7。 表1给出了在不同阵元激励幅度量化档位个数的情况下,综合方向图的性能。表中列出了赋形区域波束的波动度和副瓣区域的最高电平值两个评判标准, 阵元激励幅度的量化档位个数为12、10、8、6、4。阵元激励的幅度和相位可以看做方向图综合问题中的优化变量,因此量化档位的个数即为优化变量的自由度。当自由度大的时候,就可以得到较好的优化结果。而这一现象也从表中可以看出。当量化档位个数为12时,综合出的方向图性能和使用非幅度量化的阵元激励得到的方向图性能相似,并没有相差太多;而随着阵元激励幅度的量化档位个数减少,综合方向图的性能出现了大幅度的衰退。当档位个数为4时,综合方向图的性能已经严重失真。因此,当阵元个数固定时,量化档位越多,综合方向图效果越好。图11给出了综合方向图主瓣波动度和最高副瓣电平随阵元激励幅度量化档位变化而变化的趋势图。 图10 正方形脚印图Fig.10 Rectangular footprint 表1 不同阵元激励幅度量化档位个数下波束性能 Table 1 Beam performance with different quantizations of normalized elements excitation amplitudes 阵元激励幅度量化档位个数最大副瓣电平值/dB赋形区域波束最大波动度/dB4-14.65.86-15.92.38-18.42.010-22.41.912-23.11.9 表2给出了在相同的阵元激励幅度量化台阶个数下,不同阵列阵元数对综合方向图的性能影响。表中同样列出了赋形区域波束波动度和副瓣区域最高电平值两个评判标准,阵元激励幅度的量化档位个数为10,阵列阵元数为91、127、169、217、271和331。从表中可以看出,在同等个数的量化档位个数下,综合方向图的效果的性能和阵列阵元个数并没有线性的关系。这是因为,当阵列阵元个数变多的时候,虽然量化档位个数相对减少导致阵元激励幅度的自由度在减少,然而阵元激励相位的自由度却在增加,因此综合方向图的性能并没有过多的恶化。 图11 量化档位个数变化时综合方向图的性能曲线 Fig.11 Synthesized pattern performance curves with changing normalized element excitations amplitudes quantizations 表2 阵元激励幅度量化档位个数为10时波束性能和阵列阵元个数的关系 Table 2 Relationship between beam performance and array element numbers when quantizations of element excitation amplitudes are 10 阵列阵元个数最大副瓣电平值/dB赋形区域波束最大波动度/dB91-22.413.0127-23.003.1169-23.003.0217-22.903.2271-27.532.9 除了使用文中算法来对方向图进行仿真外,本文给出了使用其他算法来综合方向图的算例,以此来进行比较。使用粒子群算法来得到带有量化阵元激励幅值[30,31]是近来提出的一种新方法,由于其良好的综合效果而被广泛的应用于各种背景中。因此这里本文选择文献[30]和文献[31]中的两个算法来作为对比。 为了使对比更具有说服力,使用了文献[30]中的仿例作为仿真场景来完成3个算法的对比。使用的阵列为阵元数为64的线阵,阵元间距半波长,同时所有阵元均为各向同性阵元。仿真波束为一个指向零点的针状波束。图12中给出了本文算法以及文献[30]和文献[31]中算法的综合结果比较。图12(a)及图12(b)为使用本文算法得到的综合方向图以及阵元激励幅度档位分布,图12(c)及图12(d)为使用文献[30]中算法得到的综合方向图以及阵元激励幅度档位分布,图12(e)及图12(f)为使用文献[31]中算法得到的综合方向图以及阵元激励幅度档位分布。阵元激励幅度档位设置为8个档位,两个算法得到的量化阵元激励幅值均为对称式分布。使用本文算法得到的量化阵元激励幅度为(0.079 3,0.197 5,0.334 7,0.453 3,0.606 0,0.746 3,0.880 1,1),使用文献[30]中算法得到的量化阵元激励幅度为(0.075 5,0.206 4,0.360 6,0.532 5,0.698 6,0.841 1,0.945 1,1),使用文献[31]中算法得到的量化阵元激励幅度为(0.139,0.260 8,0.388 0,0.520 1,0.624 4,0.755 4,0.881 2,0.999 8)。表3给出了该对比算例中两个综合方向图的具体参数。 从图12和表3中可以看出,本文算法在阵元激励幅值动态范围一项上占有优势,在方向图性能方面略逊于文献[30,31]中的算法。然而,文献[30,31]使用了粒子群算法作为优化方法,其良好的综合结果是以综合时间以及计算复杂度作为代价来获取的。因此这里对3个算法的综合时间及计算复杂度进行分析对比。 图12 64阵元线阵的综合方向图效果对比Fig.12 Comparison of performance of synthesized pattern using linear array with 64 elements 表3 使用3个算法得到的针状波束综合效果 Table 3 Comparison of performance of pencil beam synthesis using three algorithms 算法最高副瓣电平值/dB3dB宽度/(°)阵元激励幅度动态范围/dB本文算法-33.13.8920文献[30]中算法-35.482.41825文献[31]中算法-35.592.4120 表4给出了3个算法的计算复杂度以及在综合5.4节的算例时3个算法所用时间。由于3个算法的核心及主要工作量均在于如何获取阵元激励幅度档位和加权宽度,因此这里的对比也将着重于分析获阵元激励幅度档位和加权宽度的时间及复杂度。 1) 本文对式(19)的求解使用了MATLAB中的fmincon工具箱,求解算法为序列二次规划算法(SQP)[32]。根据文献[32]中提及的sqp算法的复杂度,本文算法获取阵元激励幅度档位和加权宽度的时间复杂度可以写为O(K3.5),其中K为量化阵元激励幅度档位。 表4 使用本文算法以及文献[30,31]中算法综合针状波束的时间 Table 4 Comparison of time of pencil beam synthesis using proposed algorithm and algorithms of Refs.[30,31] 算法综合时间/s计算复杂度本文算法4.36O(K3.5)文献[30]中算法45.00O(χ1(MCI1NCP1K+MSI1NSP1K))文献[31]中算法60.00O(χ2(MCP2NCP2K+MSI2NSP2K+TpMp(Np)2)) 从上述分析中可以看出,本文算法的优点可以归纳如下: 1) 效果良好。从仿真算例可以看出,仿真结果满足大部分实际工程需求。 2) 速度快,计算步骤不繁琐。从对比中可以看出,由于计算过程较为复杂,文献[30,31]中算法的计算复杂度含有较多的变量,这些变量的取值往往大于阵元激励幅度档位个数,因此整个综合时间会受到多个变量的共同影响,这不仅会增大计算量,也对预先估计算法的运行时间增添了难度。本文算法的计算复杂度仅和量化阵元激励幅度的档位个数有关,不仅综合过程简单,同时也能提供较快的综合速度,这也是本文算法最大的优势所在。 3) 阵元激励幅值动态范围的减少也使得本文算法有着更广泛的工程应用性。 本文提出了一种如下的新型的基于幅度分档的赋形波束方向图综合算法。 1) 提出了使用概率密度理论得到量化的阵元激励幅度的方法,使得量化过程可以根据任意形状的阵面和阵元栅格排布来划分幅度的档位区间。 2) 在1)的基础上使用半松弛正定方法来得到阵元激励的相位分布,利用优化过的相位分布减小因阵元激励幅度量化所带来的误差,从而进一步提高最终方向图的性能效果。 本文实现方法简单,无需迭代,从而有着更广泛的适用性。仿真结果验证了本文方法的正确性和有效性。 [1] WARREN L, STUTZMAN A, THIELE G. Antenna theory and design[M]. New York: John Wiley & Sons, 1998: 76-171. [2] STRAIT B J. Antenna arrays with partially tapered amplitudes[J]. IEEE Transactions on Antennas & Propagation, 1967, AP15(5): 611-617. [3] HANSEN R C. Effect of field amplitude taper on measured antenna gain and sidelobes[J]. Electronics Letters, 1981, 17(7): 260-261. [4] HAUPT R L. Reducing grating lobes due to subarray amplitude tapering[J]. IEEE Transactions on Antennas & Propagation, 1985, 23(8): 119-122. [5] HAUPT R L. Optimization of subarray amplitude tapers[C]∥Antennas and Propagation Society International Symposium. Piscataway, NJ: IEEE Press, 1995, 4: 1830-1833. [6] OGG F C. Steerable array radars[J]. IRE Transactions on Military Electronics, 1961, MIL-51(2): 80-94. [7] MAFFETT A. Array factors with nonuniform spacing parameter[J]. IRE Transactions on Antennas & Propagation, 1962, 10(2): 131-136. [8] LO Y. A spacing weighted antenna array[C]∥1958 IRE International Convention Record. Piscataway,NJ:IEEE Press, 1966: 191-195. [9] WILLEY R. Space tapering of linear and planar arrays[J]. IRE Transactions & Antennas and Propagation, 1962, 10(4): 369-377. [10] ISHIRU A. Theory of unequally-spaced arrays[J]. IRE Transactions on Antennas & Propagation, 1962, 10(6): 691-702. [11] SKOLNIK M L, SHERMAN J, OGG F. Statistically designed density-tapered arrays[J]. IEEE Transactions & Antennas and Propagation, 1964, 12(4): 408-417. [12] HAUPT R L. Thinned arrays using genetic algorithms[J]. IEEE Transactions on Antennas & Propagation, 1994, 42(7): 993-999. [13] NUMAZAKI T, MANO S, KATAGI T, et al. An improved thinning method for density tapering of planar array antennas[J]. IEEE Transactions on Antennas & Propagation, 1987, 35(9): 1066-1070. [14] BALL G J. Statistical density and amplitude tapering[C]∥1989 Sixth International Conference on Antennas and Propagation. Coventry: IET, 1989: 249-253. [15] MAILLOUX R J, COHEN E. Statistically thinned arrays with quantized element weights[J]. IEEE Transactions on Antennas & Propagation, 1991, 39(4): 436-447. [16] LEE J J. Sidelobes control of solid-state array antennas[J]. IEEE Transactions on Antennas & Propagation, 1988, 36(3): 339-344. [17] XUE F, GUO Y, FANG N. Analysis and computation of circular aperture arrays with multi-step amplitude quantization[C]∥IEEE Antennas & Propagation Society International Symposium. Piscataway, NJ: IEEE Press, 1992:470-473. [18] QIN L J, SHAO J D. Design of multi-step amplitude quantized weights for solid-state planar phased array antennas[C]∥Aerospace & Electronics Conference. Piscataway, NJ: IEEE Press, 1995: 77-80. [19] TIE G, JIAN X L, YAN C G. Design and analysis of multi-step amplitude quantization weighted 2-D solid-state active phased array antennas[J]. Journal of Electronics, 1994, 11(1): 71-78. [20] HUAN Z, WANG Y X, XU X W, et al. Direct amplitude optimization and quantization for ultralow sidelobe phased arrays[C]∥IEEE International Conference on Computational Electromagnetics and Its Applications. Piscataway, NJ: IEEE Press, 1999: 183-186. [21] HUAN Z, WANG Y X, XU X W, et al. Multi-step amplitude quantization for ultralow sidelobe phased arrays by direct optimization synthesis[J]. Journal of Systems Engineering and Electronics, 2001, 12(1): 65-69. [22] XU H. Research on phased array antenna multi-step mixed feed[C]∥Microwave and Millimeter Wave Technology. Piscataway, NJ: IEEE Press, 2010: 2003-2006. [23] XU F M, MENG L Q, XIE Y N. Realizing stepped amplitude quantization of low sidelobe linear array using particle swarm optimization algorithm[C]∥IET International Communication Conference on Wireless Mobile and Computing. Coventry: IET, 2009: 570-573. [24] LUO Z Q, MA W K, SO A M C, et al. Semidefinite relaxation of quadratic optimization problems[J]. IEEE Signal Processing Magazine, 2010, 27(3): 20-34. [25] BALANIS C A. Antenna theory: Analysis and design[M]. New York: Harper & Row, Publishers, Inc.,1982: 212-216. [26] POZAR D M. The active element pattern[J]. IEEE Transactions on Antennas & Propagation, 1994, 42(8): 1176-1178. [27] HADDADI A, GHORBANI A, RASHED M J. Cosecant-squared pattern synthesis using a weighted alternating reverse projection method[J]. IET Microwaves, Antennas & Propagation, 2011, 5(15): 1789-1795. [28] BOYD S, VANDENBERGHE L. Convex optimization[M]. New York: Cambridge University Press, 2004: 51-53 [29] HUANG Y, PALOMAR D P. Rank-constrained separable semidefinite programming with applications to optimal beamforming[J]. IEEE Transactions on Signal Processing, 2010, 58(2): 664-678. [30] ZHANG Z H, HU W D, YU W X. Design of quantized amplitude weights for low sidelobe phased array antennas[J]. Acta Electronica Sinica, 2007, 35(3): 580-584. [31] 徐锋明, 孟令琴, 谢亚楠. 基于改进的粒子群算法实现阶梯幅度量化相控阵天线的低副瓣[J]. 上海大学学报(自然科学版), 2010, 16(4): 361-366. XU F M, MENG L Q, XIE Y N. Realization of low sidelobe for step-quantized amplitude phased array antennas based on modified particle swarm optimization[J]. Journal of Shanghai University (Natural Science Edition), 2010, 16(4): 361-366 (in Chinese). [32] 虞泓波, 冯大政, 解虎. 采用序列二次规划求解的稳健波束形成新算法[J]. 西安电子科技大学学报, 2016, 43(2): 41-45. YU H B, FENG D Z, XIE H. Novel robust beamforming algorithm using sequential quadratic programming[J]. Journal of Xidian University, 2016, 43(2): 41-45 (in Chinese). [33] KENNEDY J. Particle swarm optimization[M]. Encyclopedia of machine learning. Berlin: Springer, 2011: 760-766. [34] LIU Y Q, LIU S Y, GU M T. Application of powell algorithm in linear support vector machine[J]. Computer Engineering, 2011, 37(12): 161-163.
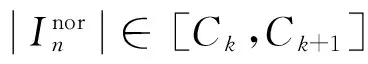



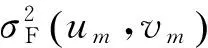
3 量化幅度加载下的阵元激励相位分布
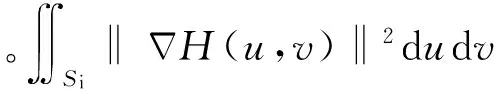

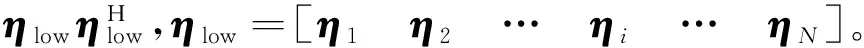

4 量化阵元激励幅度下的方向图综合步骤
5 仿真算例
5.1 平顶方向图综合



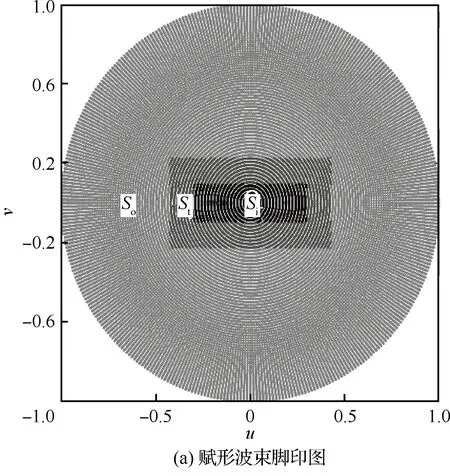
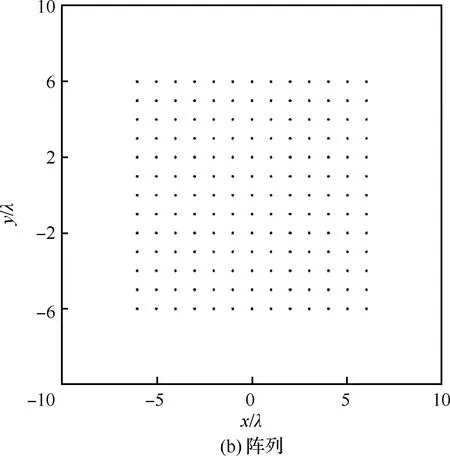
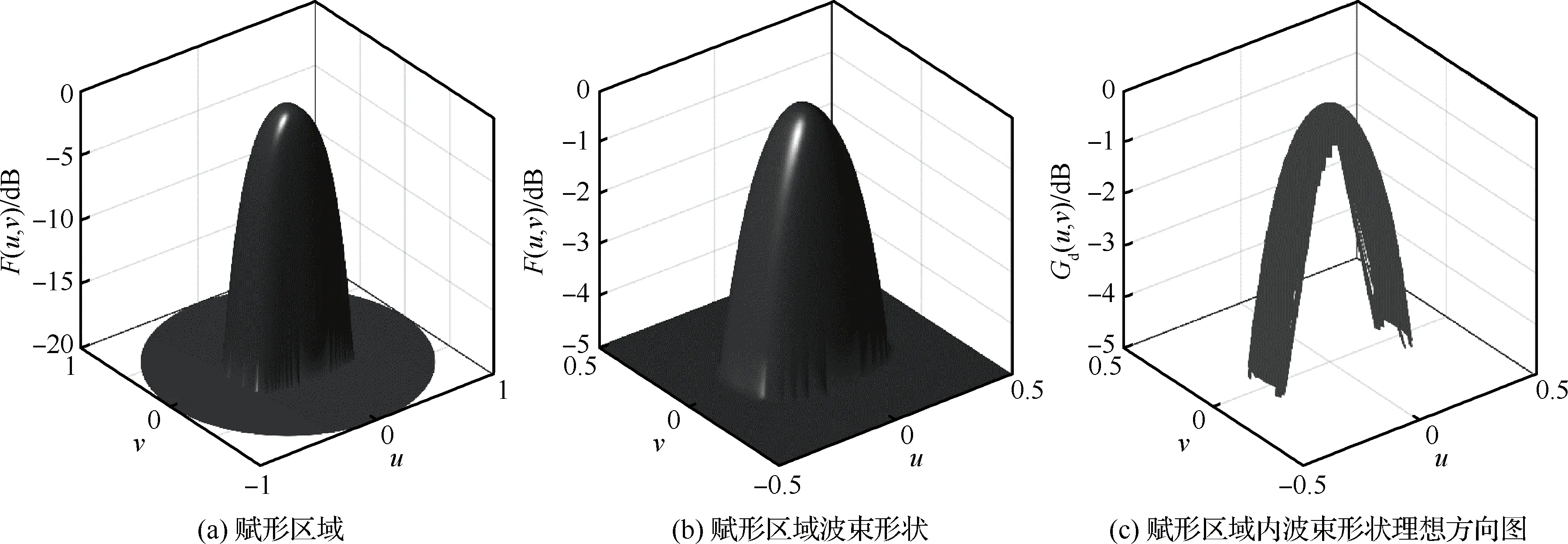
5.2 赋形方向图综合


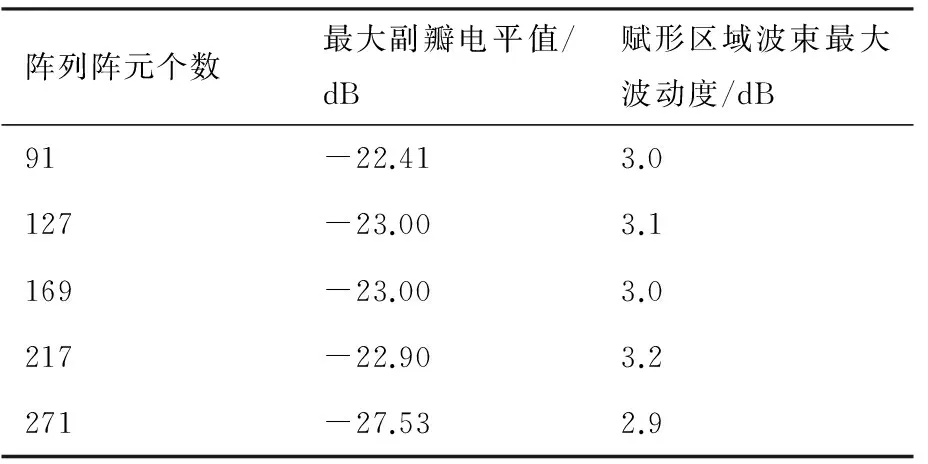
5.3 量化档位个数的影响



5.4 算例比对



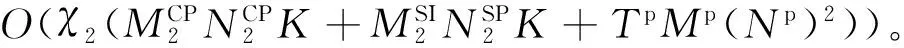
6 结 论

