DPW Ⅳ~DPW Ⅵ数值模拟技术综述
王运涛
中国空气动力研究与发展中心 计算空气动力研究所, 绵阳 621000
由AIAA发起并主导的DPW(Drag Prediction Workshop)系列会议成功举办了6届,吸引了世界范围内相关研究机构的广泛参与,已经成为CFD验证和确认领域最具代表性的国际会议之一。DPW系列会议的主要目的是评估现代CFD技术模拟运输机高速构型阻力预测能力,提供一个公开、公正的研究平台,为CFD技术下一步的发展提供意见和建议。
2001年6月召开的第1届DPW会议(DPW I)选择了DLR-F4翼身组合体构型作为基准模型,研究工况为固定升力系数的阻力预测(Case 1)与极曲线预测(Case 2),采用14种软件获得了18组Case 1的计算结果[1]。
2003年6月召开的第2届DPW会议(DPW Ⅱ)选择了DLR-F6翼身组合体构型和DLR-F6翼/身/架/舱两种高速构型作为基准模型,必选研究工况包括固定升力系数下的网格收敛性研究(Case 1)和极曲线预测(Case 2),可选工况包括固定升力系数下的转捩位置影响(Case 3)及固定升力系数下的阻力发散特性(Case 4)。这次会议的另一个研究目的是评估CFD技术模拟挂架/短舱安装阻力的能力,采用22种软件获得了29组Case 1的计算结果[2]。
由于DPW Ⅱ的数据提供者普遍碰到了翼身结合部流动局部分离导致的气动特性收敛困难,2006年6月召开的第3届DPW会议(DPW Ⅲ)选择了DLR-F6和DLR-F6_FX2B两种翼身组合体构型作为基准模型。其中DLR-F6_FX2B翼身组合体构型对DLR-F6-WB构型翼身结合部后缘进行了修型处理,并将数值模拟的雷诺数提高到500万,以避免翼身结合部的局部分离。与DPW Ⅰ和DPW Ⅱ事先公布试验结果不同,DPW Ⅲ采用了“blind test”方式开展研究工作,即数值模拟提供者事前并不知道试验结果。另外,为了鼓励更多的研究人员参与,基准模型还包括两个单独的机翼构型(DPW-W1、DPW-W2)。研究工况包括固定升力系数下的网格收敛性研究(Case 1A、Case 2A)和极曲线预测(Case 1B、Case 2B)。此次会议另一目的是评估CFD技术模拟局部修型引起气动特性差量的能力,采用18种软件获得了26组Case 1A的计算结果[3]。阎超等[4]对DPW Ⅰ~DPW Ⅳ会议的情况进行了概述。
基于前3届DPW会议的经验和教训,以及CFD验证与确认工作的迫切需求,从第4届DPW会议(DPW IV)到第6届DPW会议(DPW VI),基准模型采用了波音公司重新设计的CRM(Common Research Model)[5],并在美国、欧洲的风洞中开展了多项试验,积累了更加详细、丰富的试验数据。DPW Ⅳ~DPW Ⅵ的研究内容主要包括网格收敛性、挂架/短舱安装阻力预测、机翼下洗流动影响、马赫数/迎角影响、雷诺数影响、静气动弹性影响等。本文介绍了CRM及开展的风洞试验,概述了DPW Ⅳ~Ⅵ会议的情况,从计算网格生成、计算方法与湍流模型、计算结果与试验结果的对比、优化设计等方面总结CFD验证与确认工作的进展,并给出了进一步开展CFD验证与确认工作的思考和建议。
1 CRM及风洞试验
CRM由波音公司主导设计,主要目的是为CFD的验证和确认工作提供基本的、可公开的研究构型和丰富完备的风洞试验数据。该模型的设计综合考虑了CFD验证和确认研究工作的需求,工业部门、政府部门的建议,以及当前的气动设计和风洞试验能力。该模型选择了机身/机翼/发房/平尾构型(见图1),采用下单翼/翼吊双发布局,是典型的宽体民机布局。CRM包括了多种构型,主要有翼身组合体(CRM-WB)、翼/身/挂架/短舱构型(CRM-WBPN)、翼身组合体加0°平尾(CRM-WBT0)、加2°平尾(CRM-WBT+2)、加-2°平尾(CRM-WBT-2)这5种构型。该模型的设计马赫数为0.85,设计升力系数为0.50。该模型的参考面积Sref=383.690 m2,平均气动弦长c=7.005 32 m,展长b=58.762 9 m、梢根比λ=0.275,展弦比AR=9.0,1/4弦线后掠角Λc/4= 35.0°。
CRM的风洞试验是在NASA FA/SFW项目的资助下完成的[6-7],2010—2013年在NASA Langley的NTF(National Transonic Facility)风洞完成了两期试验(见图2),试验构型包括CRM-WB、CRM-WBPN、CRM-WBT0、CRM-WBT+2、CRM-WBT-2。马赫数Ma=0.7~0.87,雷诺数Re=5.0×106~30×106,迎角α=-3°~12°(Re=5.0×106)、α=-3°~6°(Re=19.8×106,30.0×106),温度T=-250~120 °F(1 °F=17.22 ℃) , 试验结果包括气动特性、表面压力分布及模型变形测量数据等。

图1 CRM构型Fig.1 Common research model configuration
图2 CRM在NTF风洞中的安装照片Fig.2 Photo of CRM in the National Transonic Facility (NTF) wind tunnel
2010年4月,在NASA Ames的11 ft (1 ft=304.8 mm) TWT(Transonic Wind Tunnel)风洞中完成了一期对比试验,试验构型同样是5种,试验马赫数Ma=0.7~0.87,雷诺数Re=5.0×106,迎角α=-3°~12°,温度T=100 °F。试验结果除了气动特性、表面压力分布及模型变形测量数据外,还包括压敏漆(Pressure Sensitive Paint,PSP)试验、摩阻测量和粒子图像测速(Particle Image Velocimetry,PIV)试验。2014年2月,在欧盟项目的资助下(FP/2007-2013),该模型在德国哥廷根的ETW(European Transonic Wind tunnel)又开展了一期对比试验[8],试验构型仅限于CRM-WBT0,试验马赫数、雷诺数、迎角范围与NTF相同,温度范围T=-249~83.93 °F,试验结果包括气动特性、表面压力分布及模型变形测量等。此外,2012年,日本宇航院(JAXA)也在JAXA 2 m×2 m跨声速风洞中完成了80%缩比的CRM风洞试验[9];近期,法国国家航天航空研究中心(ONERA)也在S1MA风洞中完成了CRM的风洞试验[10]。
NTF、TWT和ETW的风洞试验均采用了相同的缩比(0.027)模型,唯有尾部支撑方式和风洞试验数据修正方法略有不同,3座风洞的试验结果均已经在互联网发布。特别需要指出的是,3座风洞的试验结果均没有进行支撑干扰修正,这会对数值模拟结果与风洞试验结果的对比产生重要影响。NTF与TWT的风洞试验结果相比,相同试验条件下,升力系数与力矩系数的差别很小,阻力系数的差量在10 counts以内(1 count=0.000 1)。ETW与NTF的风洞试验结果相比,在Ma=0.85的条件下,NTF试验获得的阻力系数比ETW试验获得的阻力系数低16 counts;在Re=5.0×106的条件下,NTF试验获得的低头力矩系数小于ETW试验获得的低头力矩系数;两个风洞之间的测压试验结果吻合良好;在数据误差范围内,两个风洞之间的变形测量试验结果吻合。由以上对比可以得到如下结论:在Ma=0.85、Re=5.0×106的条件下,不同风洞之间的升力系数、压力分布、变形测量结果吻合良好,力矩系数有差异,阻力系数相差10 counts以上。
2 DPW Ⅳ~Ⅵ会议概述
DPW Ⅳ会议于2009年6月在美国德克萨斯州(Texas)的圣安东尼奥市(San Antonio)召开[11-12]。此次会议选择了CRM-WBT构型作为基准研究模型,必选工况包括固定升力系数下的网格收敛性研究(Case 1A)、下洗影响研究(Case 1B),可选工况包括阻力发散马赫数模拟(Case 2)、雷诺数影响(Case 3),采用“blind test”方式开展。来自世界各地的17个研究机构采用16款软件提供了28组Case 1A的数值模拟结果。其中,有17组结果采用了非结构网格技术,11组结果采用了结构网格技术;18组结果采用了Spalart-Allmaras (S-A) 一方程湍流模型及其修正形式,7组结果采用了Menter 剪切应力输运(SST)两方程湍流模型及其修正形式。主要结论如下:采用非结构网格技术得到的数值模拟结果的散布度要大于采用结构网格技术获得的数值模拟结果;翼身结合部后缘的分离泡尺寸散布度较大;在机翼展向η=0.845 6站位,激波位置散布度较大,但随着网格规模的增加散布度减少;大多数结果模拟CRM-WBT0、CRM-WBT+2两种构型的阻力与力矩特性相似,但模拟CRM-WBT-2构型的阻力与力矩特性差别较大;在迎角为4°时,各组结果之间力矩特性差异明显;与阻力系数和力矩系数的绝对量相比较,配平得到的阻力和水平尾翼偏角差别较小;各组结果之间阻力发散马赫数预测能力与雷诺数影响预测能力相当。
DPW Ⅴ会议于2012年6月在美国路易斯安那州(Louisiana)的新奥尔良市(New Orleans)召开[13-14]。此次会议选择了CRM-WB构型作为基准研究模型,必选工况包括固定升力系数下的网格收敛性研究(Case 1)、固定马赫数下的抖振特性研究(Case 2),可选工况包括湍流模型的确认(Case 3)。来自世界各地的22个研究机构采用17款软件提供了54组Case 1的数值模拟结果。其中,26组结果采用了非结构网格技术,12组结果采用了结构网格技术,16组结果采用了自行生成的网格;34组结果采用了Spalart-Allmaras一方程湍流模型及其修正形式,12组结果采用了Menter SST两方程湍流模型及其修正形式。主要结论如下:对于Case 1,数据散布度要小于DPW IV的结果,但依然较大;阻力系数与试验结果的对比情况要好于迎角与俯仰力矩系数与试验的对比情况。对于Case 2,采用RST模型与k-ε-RT模型的结果不理想;迎角为2.5°时,计算结果之间的吻合度较好;迎角为4.0°时,计算结果之间的分散度较大;计算得到的俯仰力矩系数与试验结果相差较大;静气动弹性变形影响显著;大迎角状态下,流动由显著的激波诱导分离所主导。
DPW Ⅵ会议于2016年6月在美国华盛顿哥伦比亚特区(Washington, D.C.)召开[15-16]。此次会议选择了包括静气动弹性变形的CRM-WB构型和CRM-WBPN构型作为基准研究模型,必选工况包括湍流模型的确认(Case 1)、固定升力系数下挂架短舱的安装阻力及网格收敛性研究(Case 2)、CRM-WB构型的静气动弹性影响(Case 3),可选工况包括CRM-WB构型的网格自适应技术(Case 4)、CRM-WB构型的流固耦合模拟(Case 5)。来自世界各地的25个研究机构采用25种软件提供了48组Case 1的数值模拟结果。其中,32组结果采用了非结构网格技术,9组结果采用了结构网格技术,5组结果采用了笛卡儿网格;36组结果采用了Spalart-Allmaras一方程湍流模型及其修正形式,6组结果采用了Menter SST两方程湍流模型及其修正形式。中国空气动力研究与发展中心(CARDC)的王运涛(TRIP(TRIsonic Platform)软件,ID号T1)、陈江涛(Mflow软件,ID号D1/D2)为此次会议提供了数值模拟结果[15]。主要结论如下:对于Case 2,挂架/短舱的安装阻力在试验结果的误差范围内;除个别采用笛卡儿网格的结果外,网格类型、湍流模型和收敛水平对机翼和短舱的压力分布基本没有影响。对于Case 3,迎角为2.5°时,计算结果之间的吻合度较好;迎角为4.0°时,计算结果之间的分散度较大;数值模拟结果过度预测了外翼载荷,导致外翼截面低头力矩过大、截面升力系数过大;计算模型中考虑静气动弹性变形大大提高了数值模拟结果与试验结果的吻合程度;大迎角状态下,流动由显著的激波诱导分离所主导。对于Case 4,模拟三维雷诺平均Navier-Stokes (RANS)方程的自适应网格技术需要进一步完善。对于Case 5,流固耦合数值模拟技术重要性凸显,但距离工程实用尚有差距。
3 CRM计算网格生成
无论对于结构网格还是非结构网格,网格的质量、规模及网格生成技术本身对于数值模拟结果的重要性不言而喻。2003年,Rumsey等[17]采用重叠网格技术,开展了典型运输机构型抖振边界附近计算结果影响因素分析,将局部网格细节处理作为一个重要的影响因素。2014年,Slotnick等[18]在总结过去10年CFD的发展概况中指出,网格生成和自适应仍是CFD工作流程中的重大瓶颈问题之一。
从DPW Ⅰ会议开始,DPW组委会就开始尝试针对所研究的基准构型开展网格生成规范研究[19-23],并从DPW Ⅱ开始引入了网格收敛性研究,作为必选工况之一。经历了DPW Ⅱ和DPW Ⅲ两次会议的不断完善,到DPW Ⅳ及以后的会议逐步形成了典型运输机构型的网格生成规范[24-27]。以CRM翼身组合体构型为例(见图3),网格生成规范包括了黏性边界层物面距离、黏性边界层内的网格增长率、机翼展向翼根和翼尖的网格分布、机翼后缘网格数目、远场边界距离以及不同规模网格之间网格数量比例等。为了吸引更多的CFD工作者广泛参与和最大限度地汲取网格生成经验,DPW组委会一方面根据不断完善的网格生成规范提供多种数据格式的基础结构网格、非结构网格,另一方面允许参与者根据自身的工程应用经验自行生成合适的网格。根据DPW历次会议的经验和教训不断总结网格生成规范的目的,一是为网格收敛性研究提供系列网格,二是减少采用结构网格、非结构网格等不同类型网格数值模拟结果之间的差异,三是逐步形成工程实用的网格生成规范。

图3 CRM-WB构型表面网格Fig.3 Surface grid of CRM-WB configuration
历次DPW会议网格生成的一个显著特点是网格规模的逐渐增加。以翼身组合体构型的中等结构网格为例,2003年DPW Ⅱ组委会提供的DLR-F6翼身组合体构型的多块对接结构网格规模为390万,2006年DPW Ⅲ组委会提供的DLR-F6-FX2B翼身组合体构型的多块对接结构网格规模为810万,2012年DPW Ⅴ组委会提供的CRM翼身组合体构型的重叠结构网格规模为570万,2016年DPW Ⅵ组委会提供的CRM翼身组合体构型的重叠结构网格规模为2 470万。CRM翼身组合体网格规模从2012—2016年增加了4.3倍,这一方面得益于高性能计算机的飞速发展,另一方面也反映了工程应用领域对网格规模无止境的需求。在这个方面, 2010年Sclafani等[24]采用重叠网格技术和24亿的网格模拟了CRM-WBT0构型,并得到了具有网格收敛性的数值模拟结果。2016年,中国空气动力研究与发展中心的TRIP软件开发小组完成了CRM-WBPN构型139亿网格的生成(见图4),并在CARDC的高性能计算机集群上采用6400 CPU核稳定运行7~24 h,完成12 000步迭代,平均残差下降4.8个量级,获得了收敛后的流场计算结果。
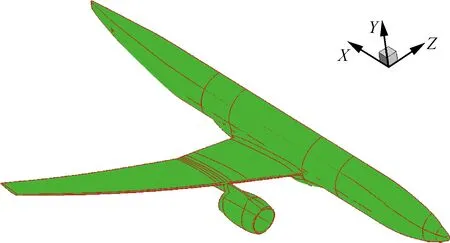
图4 CRM-WBPN构型表面网格(139亿)Fig.4 Surface grid of CRM-WBPN configuration (13.9 billion)
总结DPW Ⅳ~Ⅵ会议网格方面的研究成果,主要结论如下:网格生成技术本身没有质的突破;网格规模达到一定程度后,结构网格与非结构网格数值模拟结果相当;如何构造网格序列开展网格收敛性研究依然值得进一步探索;自适应网格技术是重要的研究方向之一。
4 计算方法与湍流模型
毫无疑问,基于RANS方程的数值模拟技术依然是现代飞行器气动设计和评估的主要工具,DPW历次会议上所提供的数值模拟结果基本上是采用RANS方程、有限体积方法和二阶空间离散精度获得的。2012年召开的第5届DPW会议(DPW Ⅴ),共有来自世界各地的22个研究团队提供了57组计算结果,全部采用了基于RANS方程的有限体积方法;2016年召开的第6届DPW会议(DPW Ⅵ),共有来自世界各地的25个研究团队提供了54组计算结果,其中23个团队采用了基于RANS方程的有限体积方法。近年来,基于五阶空间离散精度的WCNS (Weighted Compact Nonlinear Scheme)[28]格式,通过在几何守恒律方面持续不断的研究工作[29],在复杂构型数值模拟方面取得了重要进展[30-38],采用WCNS格式模拟了DLR-F6、DLR-F6/FX2B、CRM-WBH0和CRM-WB等DPW系列会议的翼身组合体构型。图5给出了采用RANS方程、有限差分方法和WCNS格式模拟CRM-WBT0构型的表面压力系数Cp云图(Ma=0.85,Re=5.0×106,升力系数CL=0.500),所采用的多块对接结构网格规模为557万。上述结果显示了WCNS格式在复杂构型方面的应用潜力。
湍流模型是影响数值模拟结果精准度的另一个重要因素。Rumsey等[17]开展了典型运输机构型抖振边界附近计算结果影响因素分析,研究的影响因素主要包括不同软件、不同湍流模型和不同局部网格细节处理,其中湍流模型的影响最大。不同湍流模型对升力系数的影响量为3.8%,对阻力系数的影响量为2.9%,对俯仰力矩的影响量为23.6%。Slotnick等[18]在总结过去10年CFD的发展概况中指出,CFD软件中复杂湍流模型的有效性和收敛性是工程应用中的重大瓶颈问题之一。正是逐步意识到了湍流模型对数值模拟结果的极端重要性,从DPW Ⅴ会议开始,DPW组委会专门选择了湍流模型的验证工况,用于验证各种CFD软件中湍流模型的正确性及工程适用性,并从DPW V会议的可选工况(Case 3)上升到DPW Ⅵ会议的必选工况(Case 1),具体工作可参考Levy[14]和Roy[39]等的文献。

图5 CRM-WBT0构型高阶精度模拟Fig.5 High-order precision simulation of CRM-WBT0 configuration
总结DPW历次会议上所提供的数值模拟结果可以看出,Spalart-Allmaras一方程湍流模型[40]及其各种修正形式和Menter SST两方程湍流模型[41]及其各种修正形式依然是目前工程应用领域主要采用的湍流模型。DPW Ⅳ会议上,17个研究团队中提供的28组结果中,18组结果采用了S-A一方程湍流模型,7组结果采用了SST两方程湍流模型;DPW Ⅴ会议上,22个研究团队中提供的57组结果中,38组结果采用了S-A一方程湍流模型,13组结果采用了SSTk-ε两方程湍流模型;DPW Ⅵ会议上,25个研究团队中提供的54组结果中,36组结果采用了S-A一方程湍流模型,8组结果采用了SSTk-ε两方程湍流模型。

图6 CRM分离泡尺寸随迎角的变化[14] Fig.6 CRM separation bubble size vs angle of attack[14]
2004年RAND公司的研究报告中指出[42],在飞行器设计相关的8个复杂流动机理研究方面,黏性流动分离的起始与发展是CFD模拟尚未很好解决的6个问题之一。图6给出了DPW Ⅴ会议上,Ma=0.85,Re=5.0×106,CL=0.500时,部分数值模拟结果得到的CRM-WB构型翼身结合部后缘局部分离区域的大小随迎角的变化[14]。其中,不同颜色的点代表了不同迎角下的数值模拟结果,WBL(Wing Butt Line coordinator)代表机翼在Y轴方向的坐标。汇总DPW Ⅳ~Ⅵ会议上CRM构型翼身结合部后缘局部分离流动数值模拟结果可以看出,在这个局部区域的流动模拟是一个难点。不仅数值模拟结果之间差异明显,而且数值模拟结果与相应的试验结果之间同样差异明显(试验结果在此种工况下没有明显的分离),更严重的情况是由于这个区域存在的虚假分离会导致计算结果很难收敛。
湍流模型的研究进展主要体现在包含QCR[43](Quadratic Constitutive Relation)修正的S-A一方程湍流模型或SST两方程湍流模型的应用研究。2012年,Yamamoto等[44]采用引入QCR修正的S-A一方程和SST湍流模型模拟了CRM-WBH0构型绕流流场,计算结果显示,采用QCR修正有效减弱了翼身结合部的虚假分离。Sclafani等[24]采用引入QCR修正的S-A模型模拟了DPW V提供的CRM-WB构型绕流流场,计算结果显示,采用QCR修正有效提高了翼身结合部的模拟精度(见图7[24],Ma=0.85,Re=5.0×106,α=4°)。在以上研究工作的推动下,2016年召开的DPW VI会议上,在36组采用S-A湍流模型的结果中,有15组采用了QCR修正。
总结DPW Ⅳ~Ⅵ会议湍流模型方面的研究成果,主要结论如下:S-A和SSTk-ε湍流模型是目前工程应用的主导;在S-A和SSTk-ε湍流模型中引入QCR修正有效提高了翼身结合部的流动模拟精度;GoldbergRT、EARSM(Explicit Algebraic Reynolds Stress Model)、RSM (Reynolds Stress Model )等湍流模型值得进一步开展研究。

图7 QCR修正对表面流线的影响 [24] Fig.7 Effect of QCR correction on surface streamline [24]
5 计算结果与试验结果对比
将计算结果与风洞试验结果相比较,是验证数值模拟结果精准度的重要手段,也是CFD确认工作的主要内容。必须指出的是应用于CFD确认工作的风洞试验与一般型号的风洞试验有很大不同,应用于CFD确认工作风洞试验的顾客是CFD工作者,Oberkampf和Trucanob[45]提出了设计CFD确认试验的7项指导原则。在不同风洞中、不同时期开展的CRM风洞试验结果为典型构型运输机高速构型的CFD确认工作提供了丰富的风洞试验数据,但在试验数据的分析和整理方面还需要进一步开展工作。
Levy等[13-14]总结了CRM风洞试验与数值模拟的不同点,主要包括:CRM风洞试验存在洞壁干扰,而CFD模拟采用了自由来流条件;CRM风洞试验存在支撑干扰,而CFD模拟不包含支撑装置;风洞试验采用固定转捩方式,而CFD模拟一般采用全湍流模拟方式;风洞试验结果包含了静气动弹性变形影响,而数值模拟采用了刚性1g外形;风洞试验结果与数值模拟结果均存在不确定性和误差;风洞试验结果对已知的影响因素做了各种修正(支撑干扰除外),而数值模拟结果没有做修正。上述6个方面将对数值模拟结果与风洞试验结果的对比分析产生重要影响。以下将重点从固定升力系数下的气动特性、压力分布对比,CRM模型挂架/短舱的安装阻力对比,气动特性随迎角的变化,流固耦合数值模拟等5个方面归纳总结DPW Ⅳ~Ⅵ会议上数值模拟结果与风洞试验结果的对比情况。
1) 气动特性对比(CL≈0.500)
为鼓励更多的CFD工作者参与会议,历次DPW组委会均按预先约定的网格规范提供了至少3套不同规模的粗(Coarse)、中(Medium)、细(Fine)网格用以开展网格收敛性研究,其中,中等网格是目前工程应用方面普遍采用的网格规模,以下各节数值模拟结果与试验结果的对比均以中等网格的统计分析结果为主。
DPW Ⅴ和DPW Ⅵ两次会议上的CRM-WB构型不同点在于,采用ETW风洞试验数据,DPW Ⅵ会议提供的CRM-WB构型包含了不同来流迎角下的静气动弹性变形。图8给了CRM-WB构型不同迎角下静气动弹性变形风洞试验测量结果,其中,横坐标为机翼展向的不同站位,纵坐标为静气动弹性导致的扭转角,升力系数为0.5的数据是插值得到的;不同颜色的曲线代表了不同来流迎角下测量得到的静气动弹性变形(A2.5即迎角为2.5°)。基于风洞试验中测量得到的风洞模型静气动弹性变形数据,David[46]研究了CRM翼身组合体模型静气动弹性变形对数值模拟结果的影响;Keye等[47-48]采用流固耦合方法研究了静气动弹性变形对CRM翼身组合体模型数值模拟结果的影响;这些工作直接促成了DPW Ⅵ组委会在CRM-WB计算模型中考虑了静气动弹性变形的影响。

图8 由风洞测量数据获得的静气动弹性扭转分布[15] Fig.8 Distribution of static aeroelastic twist derived from wing tunnel measurement data[15]
表1给出了DPW Ⅴ和DPW Ⅵ会议上CRM-WB构型的“core solutions”统计结果[49-50],计算状态为Ma=0.85、Re=5.0×106、CL=0.500±0.001。其中,“Median”代表各家数值模拟结果的中位数,“Deviation”代表统计结果的均方误差,CL为升力系数,CD为阻力系数,CDp为压差阻力系数,CDf为摩擦阻力系数,Cm为俯仰力矩系数。
从表1可以得到如下基本结论:① 网格规模的增加并没有降低统计分析结果的均方误差,反而普遍有所增加(DPW Ⅵ组委会提供的基础网格规模是DPW Ⅴ组委会提供的基础网格规模的4.3倍), 如阻力系数的均方误差由DPW Ⅴ统计结果的3.2 counts增加到DPW Ⅵ统计结果的4.4 counts; ② 数值模拟得到的阻力系数散布度与试验结果之间差量相当,来流迎角与俯仰力矩系数的散布度大于试验结果之间的差量。DPW Ⅵ会议上,阻力系数的均方误差为4.4 counts,略小于风洞试验结果之间7.5 counts的阻力差异;③ 来流迎角的均方误差是试验结果之间差量的两倍,俯仰的均方误差比试验结果之间的差量大了一个量级; ④ 计算模型中考虑了静气动弹性变形后,气动特性的绝对量与试验结果之间的差异明显减少。

表1 CRM-WB构型数值模拟结果的中位数及均方差和风洞试验结果[49-50]

图9 包含/不包含模型支撑装置压力系数差量云图[52]Fig.9 ΔCp contours with/without support system of model[52]
由表1可以看出,计算模型中考虑了静气动弹性变形后,数值模拟得到的来流迎角、阻力系数和俯仰力矩系数与试验结果仍有较大差异,其主要原因是计算模型中没有考虑支撑装置与固定转捩位置的影响。有关CRM支撑干扰的研究工作最早是由NASA Langley研究中心的Rivers等[51-52]完成的。文献[51] 采用USM3D软件研究了CRM-WBT0模型支撑装置对气动特性数值模拟结果的影响,文献[52]在上述工作的基础上,又进一步考虑了CRM-WBT0模型静气动弹性变形对数值模拟结果的影响。Rivers等的数值模拟结果表明(见图9,ΔCp为无量纲压力系数差量),在Ma=0.85、Re=5.0×106、α=2°条件下,在计算模型中同时考虑静气动弹性变形和模型支撑装置,使得升力系数下降0.026 0、阻力系数下降3.7 counts、俯仰力矩系数增加0.035 9,数值模拟结果更接近风洞试验结果。针对CRM-WBH0构型,Zilliac等[53]采用OVERFLOW软件研究了固定转捩位置对阻力系数数值模拟结果的影响。研究表明:在Ma=0.85、Re=5.0×106、α=2°条件下,在风洞试验机翼的10%固定转捩位置前,采用“全湍流”模拟方式模拟得到的阻力系数大了6.4 counts,占总阻力系数的2.3%。
2) 压力分布对比(CL≈0.500)
气动特性数值模拟结果与风洞试验结果的对比属于宏观量的对比,压力分布数值模拟结果与风洞试验结果的对比则属于微观量的对比。压力分布计算结果与试验结果的对比可以进一步揭示二者之间升力和力矩等宏观量差异的原因。

图10 来自DPW Ⅴ的压力系数分布对比[13]Fig.10 Comparison of pressure coefficient distributions from DPW Ⅴ[13]
图10给出了DPW Ⅴ会议上,CRM-WB构型机翼η=0.727、0.950站位上,Ma=0.85、Re=5.0×106、CL=0.500条件下,采用中等网格获得的压力系数计算结果与相邻迎角NTF测压风洞之间的比较[13],其中,曲线代表采用不同网格形式获得的计算结果,黑色点代表相近升力系数下的测压试验结果。由DPW Ⅴ会议上压力分布的统计结果可以看出,在机翼η=0.50站位以内,数值模拟结果与风洞试验结果之间吻合良好;随着机翼站位向翼梢方向移动,数值模拟结果与风洞试验结果之间吻合度逐渐变差,主要表现在:相对于风洞试验结果,数值模拟得到的机翼上翼面激波位置普遍靠后;翼梢处,数值模拟得到的机翼前缘压力分布普遍高于风洞试验结果。导致上述差异的主要原因是DPW Ⅴ会议所提供CRM-WB构型没有包含风洞试验中模型静气动弹性变形的影响。

图11 来自DPW Ⅵ的压力系数分布对比[14]Fig.11 Comparison of pressure coefficient distributions from DPW Ⅵ[14]
与DPW Ⅴ会议所提供CRM-WB构型不同,DPW Ⅵ会议所提供的CRM-WB构型包含了ETW中测量得到的静气动变形。图11给出了DPW Ⅵ会议上,CRM-WB构型机翼η=0.603、0.950站位上,Ma=0.85、Re=5.0×106、CL=0.500条件下,采用密网格获得的压力系数计算结果与相近升力系数Ames风洞测压结果之间的比较[14],其中,不同颜色曲线代表采用不同湍流模型获得的计算结果,蓝色点代表相应的试验结果。由DPW Ⅵ会议上压力分布的统计结果可以看出,考虑了静气动弹性变形后,在机翼η=0.500站位以内,数值模拟结果与风洞试验结果之间吻合良好;在机翼η=0.603站位上,数值模拟得到的机翼上翼面激波位置明显比相应的试验结果靠后;在机翼η=0.950站位上,数值模拟得到的压力分布与风洞测压结果之间的吻合程度大大改善。导致η=0.603站位上数值模拟与试验之间激波位置差异的主要原因是DPW Ⅵ会议所提供CRM-WB构型的数值模拟结果没有包含风洞模型支撑装置的影响。
基于DPW Ⅵ会议所提供的CRM-WB构型、CRM-WB风洞试验模型的有限元模型和NASA的CRM模型官方网站提供的NTF风洞模型支撑数据,中国空气动力研究与发展中心的TRIP软件开发小组数值模拟了同时包含静气动弹性变形和模型支撑装置的CRM-WB构型气动特性[54]。图12给出了机翼η=0.727、0.950站位上,Ma=0.85、Re=5.0×106、α=2.75°条件下,CRM-WB构型的CFD计算结果(CRM-WB_CFD)、包含支撑装置的CRM-WB构型的CFD计算结果(CRM-WBS_CFD)和包含支撑装置的CRM-WB构型的流固耦合计算结果(CRM-WBS_FSC)以及相邻迎角下NTF测压试验结果。其中横坐标x/c为流向无量纲距离。比较CRM-WB_CFD和CRM-WBS_CFD的结果可以看出,模型支撑装置的影响主要使得机翼上翼面的激波位置前移。比较CRM-WBS_CFD和CRM-WB_FSC的结果可以看出,计算模型中考虑机翼的静气动弹性变形,不仅使得η=0.727站位上的激波位置进一步前移,而且显著降低了机翼上翼面激波位置前的压力系数;η=0.950站位上,静气动弹性变形使得激波位置后移,并且显著降低了机翼上翼面激波位置前的压力系数。总之,综合考虑了机翼静气动弹性变形和模型支撑装置后,数值模拟得到了压力系数分布更加接近试验结果。
3) 挂架短舱的安装阻力对比(CL=0.500)
评估现代CFD技术模拟计算构型变化导致的气动特性变化的能力,一直是DPW系列会议的研究内容之一。DPW Ⅱ会议上评估了DLR-F6构型挂架/短舱安装阻力的模拟能力[2,55],DPW Ⅲ会议上评估了DLR-F6构型翼身结合部局部修型导致的气动特性微小变化的模拟能力[3,37,56]。DPW Ⅵ会议上开展了CRM构型挂架/短舱安装阻力数值模拟能力的评估。
表2给出了文献[50]统计得到的CRM-WBPN和CRM-WB两种构型气动特性差量的中位数及均方差,同时给出了NTF和Ames风洞试验结果,计算状态为Ma=0.85、Re=5.0×106、CL=0.500。由表中可以看出,DPW会议上各数值模拟结果得到的来流迎角差量、阻力系数差量与相应的试验结果吻合良好,数值模拟结果之间的散布度较小,阻力系数的差量主要来自摩擦阻力系数;俯仰力矩系数差量与试验结果有一定差距,但各种软件数值模拟结果之间的一致性较好。

图12 CRM-WB构型的压力系数分布对比Fig.12 Comparison of pressure coefficient distributions of CRM-WB configuration
表2 中等网格ΔCD计算结果的中位数及均方差和风洞试验结果[50]
Table 2 Core medians and standard deviations of numerical solutions for ΔCD with medium grid and wind tunnel test results[50]

SourceΔα/(°)ΔCDΔCDpΔCDfΔCmDPWⅥMedian0.1640.002290.000560.001690.0056Deviation0.0070.000130.000130.000050.0007TestNTF-1970.1500.002300.0100Ames-2160.1510.002300.0100
与DPW Ⅱ和DPW Ⅲ会议上统计分析所得到的结论一致。目前的CFD软件可以较好地模拟由于计算构型的变化引起的气动特性差量。
4) 气动特性随迎角的变化(Ma=0.85)
评估现代CFD技术模拟典型运输机构型气动特性随迎角变化的能力,是CFD确认工作的主要内容,也始终是DPW系列会议的重要研究内容之一。

DPW Ⅴ会议上采用了CRM-WB构型作为基准研究模型, 图14给出了DPW Ⅴ会议上各家参与单位给出的升力系数、力矩系数与试验结果的比较[14]。其中, 不同颜色的曲线代表各家参与单位给出的数值模拟结果,空心圆圈标记代表NTF、TWT风洞的试验结果,实心圆圈标记代表了“伪试验结果”(Pseudo Wind Tunnel Data,因为Rivers等考虑了静气动弹性气动特性数值模拟结果,根据在风洞试验结果中扣除了气动弹性变形影响后得到的结果)。本次会议上数值模拟得到的气动特性与相应风洞试验结果的对比是非常令人失望的[13],这种现象在DPW Ⅳ会议上同样存在[51-52]。主要表现在:相同迎角下,数值模拟得到的升力系数普遍大于试验结果;相同升力系数下,数值模拟得到的低头力矩系数普遍大于试验结果。主要受Rivers等[51-52]有关CRM-WBH0模型静气动弹性变形和模型支撑装置对气动特性影响的研究工作启发, DPW Ⅴ组委会构造了“伪试验结果”,以期在相近构型的基础上,开展数值模拟结果与风洞试验结果的对比。

图13 CRM-WBH0构型的极曲线[12]Fig.13 Polars of CRM-WBH0 configuration[12]

图14 CRM-WB构型的升力系数和力矩系数曲线(DPW Ⅴ)[14]Fig.14 Lift and pitching moment coefficients curves of CRM-WB configuration (DPW Ⅴ)[14]
由图14可以看出,部分数值模拟结果在迎角3.0°~4.0°之间升力系数出现了过早的下降,这明显与相应的试验结果不符。其根本原因是,这些数值模拟结果在相应的迎角状态下,在翼身结合部和机翼后缘出现了大范围的虚假分离。剔除这部分结果后(47组结果中剩余26组结果),数值模拟结果与“伪试验结果”之间的比较见图15[14]。其中,不同颜色曲线代表部分参与单位采用不同湍流模型得到的数值模拟结果,实心圆圈标记代表了“伪试验结果”。由图可以看出,计算结果之间的数据散布度随着迎角增加而逐渐增加,在迎角为4.0°时,升力系数的数值模拟结果之间相差0.055,力矩系数的数值模拟结果之间相差0.043。造成这种现象的主要原因是不同的数值模拟结果在机翼上翼面激波位置和机翼后缘分离区的模拟上存在明显的差异。

图15 CRM-WB构型的升力系数和力矩系数曲线(DPW Ⅴ,剔除不合理结果)[14]Fig.15 Lift and pitching moment coefficients curves of CRM-WB configuration (DPW Ⅴ, minus outliers)[14]
图16[14]给出了数值模拟得到的极曲线与NTF、Ames试验结果的对比。其中,不同颜色曲线代表部分参与单位采用不同湍流模型得到的数值模拟结果,空心标记代表NTF、TWT风洞的试验结果。由图看出,相同升力系数下,阻力系数数值模拟结果的散布度随迎角的增加而增加;升力系数小于0.6时,阻力系数数值模拟结果的散布度与风洞试验结果之间的差量相仿。

图16 CRM-WB构型的极曲线(DPW Ⅴ)[14]Fig.16 Polars of CRM-WB configuration (DPW Ⅴ) [14]
汲取DPW Ⅳ、DPW Ⅴ两次会议的经验和教训,采用ETW风洞试验的变形测量数据,DPW Ⅵ组委会选择了包含静气动弹性变形的CRM-WB构型作为基准研究模型。需要说明的是,风洞试验中,在不同的迎角下,机翼所承受的气动载荷不同,机翼的静气动弹性变形也不同(图8)。因此,DPW Ⅵ会议上的Case 3本质上包括了7种构型。
图17[15]给出了DPW Ⅵ会议上所有计算结果的升力系数和俯仰力矩系数曲线与风洞试验结果的对比。其中,不同颜色曲线代表参与单位采用不同湍流模型得到的数值模拟结果,空心与实心的圆圈标记分别代表NTF、TWT风洞试验结果。由图17可以看出,与DPW Ⅴ的相应结果相比较(图14),计算模型中考虑了静气动弹性变形后,气动特性数值模拟结果与试验结果的吻合程度显著提高,但部分数值模拟结果依然在迎角为3.0°~4.0°之间出现了升力系数过早的下降。升力系数过早失速问题也是DPW历次会议重点研究的问题之一,讨论的焦点主要集中在:较大迎角下,RANS方程是否适用?是否URANS方程或则DES方法更适合描述这种流动?剔除这部分结果后(40组结果中剩余21组结果),数值模拟结果与风洞试验结果之间的比较见图18[15]和图19[15]。

图17 CRM-WB构型的升力系数和力矩系数曲线(DPW Ⅵ)[15]Fig.17 Lift and pitching moment coefficients curves of CRM-WB configuration(DPW Ⅵ) [15]
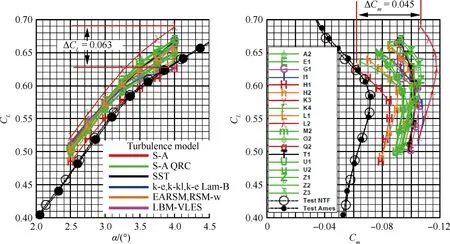
图18 CRM-WB构型的升力系数和力矩系数曲线(DPW Ⅵ,剔除不合理结果)[15]Fig.18 Lift and pitching moment coefficients curves of CRM-WB configuration (DPW Ⅵ, minus outliers)[15]
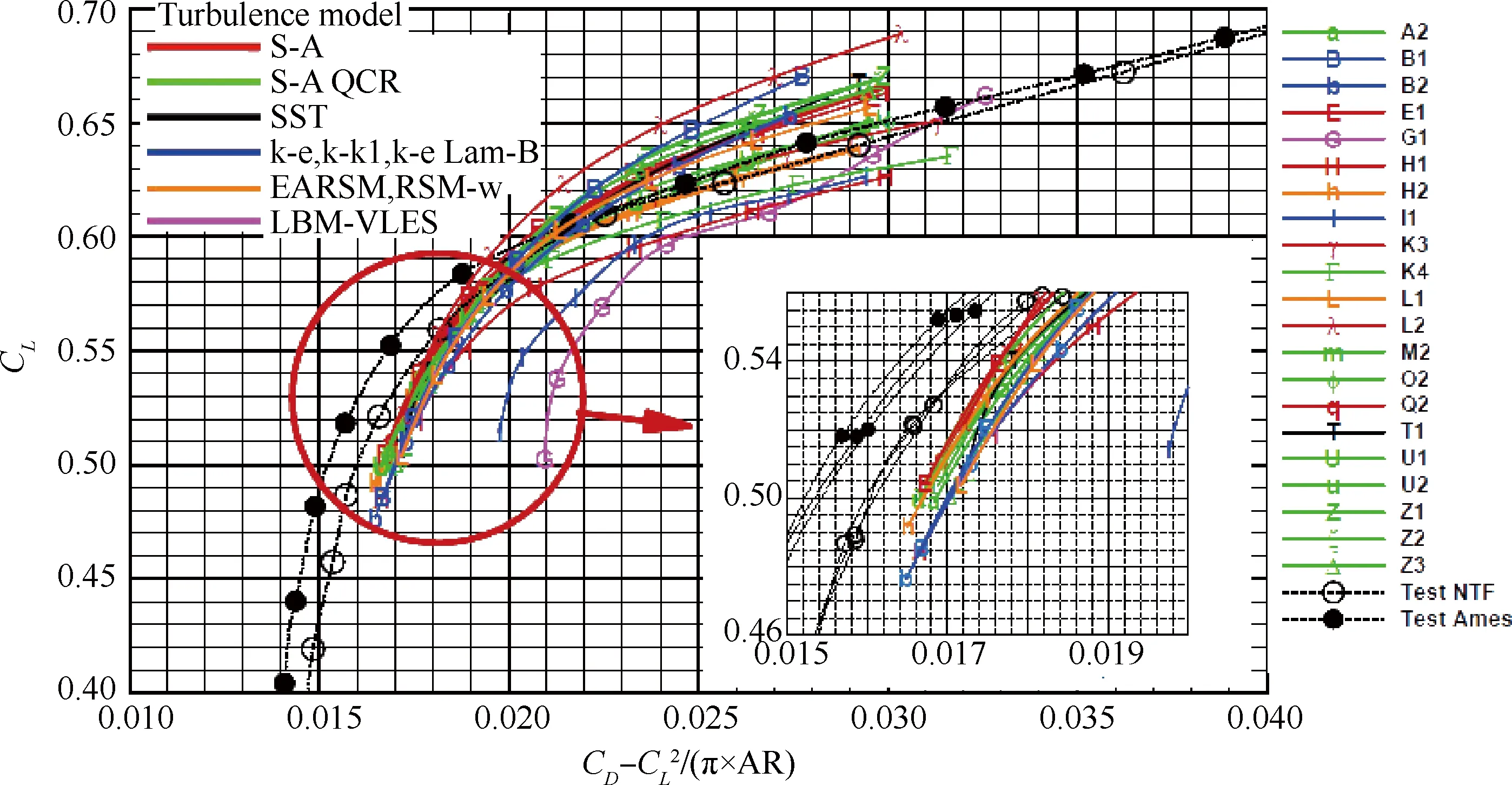
图19 CRM-WB构型的极曲线(DPW Ⅵ)[15]Fig.19 Polars of CRM-WB configuration (DPW Ⅵ)[15]
图18给出了剔除“outliers”后,数值模拟得到的升力系数与俯仰力矩系数曲线与NTF和Ames试验结果之间的比较,图中的各种标识与图17相同。由图可以看出,与DPW V的统计结果相类似,数值模拟结果之间的数据散布度依然随着迎角增加而逐渐增加,在迎角为4.0°时,升力系数的数值模拟结果之间相差0.063,力矩系数的数值模拟结果之间相差0.045。让人沮丧的是,从DPW Ⅴ~DPW Ⅵ,虽然中等网格的规模增加4倍多,但4°迎角条件下,数值模拟结果之间的散布度不仅没有减少,反而略有增加。图19给出了数值模拟得到的极曲线与NTF、Ames试验结果的对比,图中的各种标识与图17相同。由图看出,与DPW Ⅴ的统计结果相类似,相同升力系数下,阻力系数数值模拟结果的散布度随迎角的增加而增加;升力系数小于0.6时,阻力系数数值模拟结果的散布度与风洞试验结果之间的差量基本相当。
5) 流固耦合数值模拟(Ma=0.85)
静气动弹性变形对典型运输机构型气动特性的影响一直受到气动工作者的关注[57-59],2012年AIAA发起的第1届气动弹性预测研讨会AePW (Aeroelastic Prediction Workshop)[60],同样包含了静气动弹性变形预测研究。目前,借助CFD手段研究静气动弹性变形对气动特性数值模拟结果的影响一般采用两种方式:① 通过风洞试验测量得到模型在气动载荷作用下的静气动弹性变形,通过几何重构方法构建出模型变形后的外形,利用CFD方法计算变形前后外形的气动力差异;② 采用风洞试验模型的气动外形和相应的结构有限元模型,通过气动/结构耦合数值模拟方法研究静气动弹性变形对气动特性数值模拟结果的影响。
采用风洞试验测量得到的静气动弹性变形,Rivers等[51-52]开展了CRM-WBT0模型支撑装置和静气动弹性变形对数值模拟结果的影响,David[46]研究了CRM-WB模型静气动弹性变形对数值模拟结果的影响。Keye等[48]采用流固耦合方法研究了静气动弹性变形对CRM-WB模型数值模拟结果的影响。DPW Ⅵ会议上[15]的研究工况Cases 2~4本质上是采用风洞试验测量得到的静气动弹性变形重构CRM-WB构型的几何数模,进而研究静气动变形对气动特性数值模拟结果的影响;研究工况Case 5是采用流固耦合方法研究静气动弹性变形对气动特性数值模拟结果的影响。Keye和Mavriplis[16]总结了DPW Ⅵ会议上4组流固耦合数值模拟结果(图20)。其中,J4、V5代表CFD++软件提供的结果,L2代表Tau软件提供的结果,T1代表TRIP软件提供的结果。主要结论如下:4组流固耦合数值模拟结果之间差异很小,采用流固耦合方法得到的气动特性与压力分布结果合理,静气动弹性数值模拟方法远未成熟。
从图18可以看出,计算模型中考虑了静气动弹性变形影响后,CRM-WB模型气动特性数值模拟结果与试验结果之间的吻合程度有了明显的改善,但依然存在明显差异。计算模型中没有考虑支撑装置影响是主要原因之一。利用DPW组委会提供的CRM-WB计算模型、结构有限元模型(图21)和支撑模型,采用结构网格技术(图22),TRIP软件开发小组[56]采用流固耦合计算方法开展了包括支撑装置的CRM-WB构型(CRM-WBS)数值模拟,详细研究了风洞模型支撑装置和静气动弹性变形对CRM-WB构型气动特性数值模拟结果的影响。
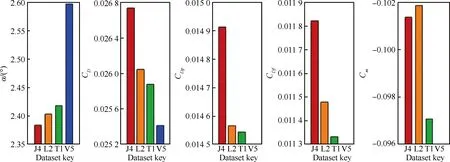
图20 CRM-WB构型流固耦合计算结果[16]Fig.20 Simulation results of fluid/structure coupling of CRM-WB configuration[16]

图21 CRM-WB风洞试验有限元模型Fig.21 Finite element model for CRM-WB wind tunnel test

图22 CRM-WBS构型网格拓扑和对称面网格 (局部)Fig.22 Grid topology of CRM-WBS configuration and grids at symmetric plane (local)



图23 CRM 翼身组合体构型的气动特性Fig.23 Aerodynamic characteristics of CRM wing-body configuration
图23给出了CRM-WB构型CFD数值模拟结果(CRM-WB_CFD)、CRM-WBS构型CFD数值模拟结果(CRM-WBS_CFD)和流固耦合(CRM-WBS_FSC)数值模拟结果,同时还给出了NTF测力试验结果。来流条件为:Ma=0.85,Re=5.0×106,α=0°~4.00°;流固耦合计算时,速压q=61.062 kPa,载荷因子q/E=3.342×10-7。对比CRM-WBS构型与CRM-WB构型的CFD数值模拟结果可以看出,在α≤3.75°范围内,模型支撑装置使得升力系数、阻力系数下降,低头力矩减少。对比CRM-WBS构型的CFD结果与CRM-WBS构型的流固耦合数值模拟结果可以看出,在计算迎角范围内,静气动弹性变形使得升力系数、阻力系数进一步下降,低头力矩进一步减少。采用流固耦合方法得到的CRM-WBS构型升力系数和阻力系数的计算结果更加接近试验值;俯仰力矩系数计算结果与试验结果的吻合程度得到进一步改善,但依然有一定的差距。另外值得关注的一点是,不包含支撑装置的CRM-WB_CFD数值模拟结果失速迎角在3.75°,而包含支撑装置的CRM-WBS_CFD与CRM-WBS_FSC的数值模拟结果直到迎角4.00°还没有出现失速。数值模拟结果与风洞试验结果之间的差异需要从风洞试验数据的修正和数值计算方法两个方面进一步开展研究工作。
6 CRM的优化设计
由于DPW系列会议持续扩大的影响力,与CRM相关的研究工作也陆续展开。其中,CRM的气动优化设计、气动/结构优化设计是当前非常活跃的一个研究方向。
Lyu等[61]基于RANS方程求解器和离散伴随方法算法,开展了CRM机翼在多种约束条件下的单点优化设计、多点优化设计工作(图24[61]),相对于原始外形,单点气动优化设计使得阻力系数降低8.5%。Kenway和Martins等[62]采用RANS方程求解器和梯度优化算法,完成了CRM-WBH构型考虑抖振起始约束的多个单点和多点优化算例(图25[62]),获得了较好的气动优化效果。陈颂等[63]针对CRM-WBH构型开展了基于离散伴随技术的气动外形优化设计方法研究,进行了有/无力矩配平约束的优化设计。刘峰博等[64]发展了基于离散伴随方法的梯度计算模块,对CRM翼身组合体构型进行了单点减阻优化设计。

图24 CRM机翼单点和多点气动外形优化[61]Fig.24 Single-point and multi-point aerodynamic shape optimization of CRM wing[61]

图25 CRM-WBH构型单点和多点气动外形优化[62] Fig.25 Single-point and multi-point aerodynamic shape optimization of CRM-WBH configuration[62]
Liem等[65]采用Kriging代理模型方法,实现了28种飞行条件、158个约束和448个气动/结构设计变量下,CRM-WBH构型的气动/结构多点综合优化(图26),以及平均燃油消耗降低8.8%的优化设计目标。Gaetan等[66]采用气动/结构耦合伴随方法,分别以起飞重量最小和燃油消耗最少为优化设计目标,完成了CRM-WBH构型476个设计变量多点优化算例(图27),分别实现了起飞重量降低4.2%、燃油消耗降低6.6%和燃油消耗降低11.2%、起飞重量基本不变的设计目标。

图26 CRM-WBH构型气动/结构分析(Ma=0.85)[65]Fig.26 Aerostructural analysis for CRM-WBH configuration at Ma=0.85[65]
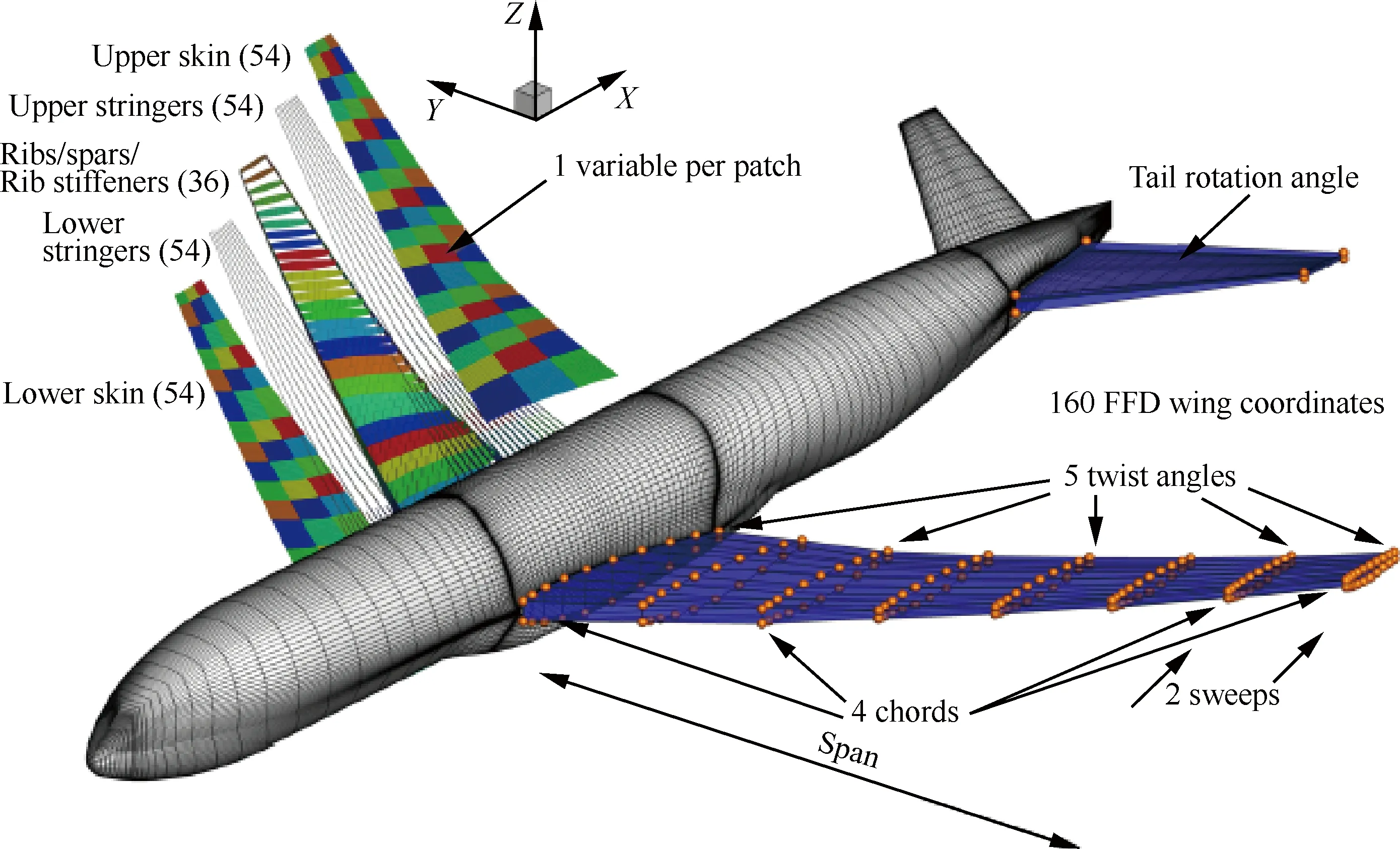
图27 CRM-WBH构型气动/结构综合优化设计变量[66]Fig.27 Aerostructural optimization design variables for CRM-WBH configuration [66]
7 CFD验证与确认工作的思考与建议
从2001—2016年,DPW会议已经连续举办了6届,其影响力已经超出了典型运输机高速巡航构型气动特性的预测这一范围。基于DPW系列会议的成功经验,AIAA又发起了高升力预测研讨会(High Lift Prediction Workshop, HiLiftPW)、气动弹性预测研讨会(AePW),与CFD技术和CRM相关的其他研究工作也在逐渐展开。本文总结DPW系列会议的成功经验,主要有以下思考和建议:
1) CFD的验证工作进展缓慢,需要进一步开展CFD验证方法的研究。CFD的验证工作本质上是个数学问题,主要研究CFD计算模型(方法、软件)、表达概念模型(如RANS方程)及其数值解准确程度的测度过程。网格收敛性研究是DPW系列会议采用的主要验证手段,Richardson外插方法是获得网格无关解的主要方法。这种方法存在的主要问题是:第一,如何构造相容的网格序列开展网格收敛性研究?虽然,在典型运输机构型网格生成规范方面,DPW组委会开展了大量的工作,但如何构造相容的网格序列依然是一个悬而未决的问题。第二,Richardson外插方法是否有效?在RANS方程二阶空间离散精度的前提下,网格规模的-2/3次幂仅仅是网格间距的定性度量,只能给出网格间距的一个趋势;另外,即使按照DPW总结的网格生成规范生成不同规模的数值模拟网格,许多软件并不能得到单调变化的气动特性收敛曲线,这种情况下靠最密与次密的气动结果外插得到的网格无关解的有效性就值得商榷。
2) 系统地开展CFD的确认工作时,不仅所研究的飞行器构型应该从简单的部件逐渐过渡到复杂组合体,研究的物理量也应该从宏观物理量(升力、阻力、力矩……)逐渐过渡到微观物理量(边界层速度型、局部表面分离流态、空间流动结构、摩擦阻力分布、典型站位压力分布……)的对比。数值模拟结果与风洞试验结果微观物理量的对比分析,不仅可以进一步解释不同研究手段获得宏观量之间的差异(不同研究手段获得的宏观物理量的差异是必然存在的),更可以为计算方法、湍流模型等数值模拟结果影响因素的改进指明方向。这就要求进一步开展精细的风洞测试技术研究,尤其是非接触测量技术研究,如压敏漆技术、温敏漆技术、粒子图像测速技术、转捩测量技术等,以便为CFD的确认工作提供丰富的试验数据。
3) 将数值模拟结果与风洞试验结果对比分析是CFD确认工作的主要手段,在进行数值模拟结果与风洞试验结果的对比前,必须先确认:第一,数值模拟所采用的外形与相应风洞试验的模型是否一致;第二,数值模拟所采用的边界条件究竟与风洞试验的条件有哪些不同;第三,风洞试验结果的同期或不同期的重复性精度是多少;第四,风洞试验结果处理的基本方法及误差。
致 谢
感谢张玉伦、洪俊武、王光学、张书俊、孟德虹、孙岩、李伟、杨小川等同志坚持不懈的努力,感谢李松同志收集了部分国内研究资料,感谢国内同行长期以来对TRIP软件开发小组的坚定支持。
[1] LEVY D W, VASSBERG J C, WAHLS R A, et al. Summary of data from the First AIAA CFD Drag Prediction Workshop[J]. Journal of Aircraft, 2003, 40(5): 875-882.
[2] LAFLIN K R, VASSBERG J C, WAHLS R A, et al. Summary of data from the Second AIAA CFD Drag Prediction Workshop[J]. Journal of Aircraft, 2005, 42(5):1165-1178.
[3] VASSBERG J C, TINOCO E N, MANI M, et al. Abridged summary of the Third AIAA CFD Drag Prediction Workshop[J]. Journal of Aircraft, 2008, 45(3): 781-798.
[4] 闫超, 席柯, 袁武力, 等. DPW系列会议述评与思考[J]. 力学进展, 2011, 41(6): 776-784.
YAN C, XI K, YUAN W L, et al. Review of the drag prediction workshop series[J]. Advances in Mechanics, 2011, 41(6): 776-784 (in Chinese).
[5] VASSBERG J C, DEHAAN M A, RIVERS S M, et al. Development of a common research model for applied CFD validation studies: AIAA-2008-6919[R]. Reston, VA: AIAA, 2008.
[6] RIVERS M B, DITTBEMER A. Experimental investigation of the NASA common research model: AIAA-2010-4218 [R]. Reston, VA: AIAA, 2010.
[7] RIVERS M B, DITTBEMER A. Experimental investigation of the NASA common research model in the NASA Langley transonic facility and NASA Ames 11-ft transonic wind tunnel: AIAA-2011-1126 [R]. Reston,VA: AIAA, 2011.
[8] RIVERS M B, RUDNIK R, QUEST J. Comparison of the NASA common research model European transonic wind tunnel test data to NASA test data: AIAA-2015-1093 [R]. Reston: AIAA,VA, 2015.
[9] UENO M, KOHZAI T, KOGA S, et al. 80% scaled NASA common research model wind tunnel test of JAXA at relatively low Reynolds number: AIAA-2013-0493[R]. Reston,VA: AIAA, 2013.
[10] CARTIERI A, HUE D, CHANZY Q, et al. Experimental investigations on the common research model at ONERA-S1MA—Comparison with DPW numerical results: AIAA-2017-0964 [R]. Reston,VA: AIAA, 2017.
[11] VASSBERG J C, TINOCO E N, MANI M, et al. Summary of the Fourth AIAA CFD Drag Prediction Workshop: AIAA-2010-4547[R]. Reston,VA: AIAA, 2010.
[12] VASSBERG J C, TINOCO E N, MANI M, et al. Summary of the Fourth AIAA Computational Fluid Dynamics Drag Prediction Workshop[J]. Journal of Aircraft, 2014, 51(4): 1070-1089.
[13] LEVY D W, LAFLIN K R, TINOCO E N, et al. Summary of data from the Fifth Computational Fluid Dynamics Drag Prediction Workshop: AIAA-2013-0046[R]. Reston,VA: AIAA, 2013.
[14] LEVY D W, LAFLIN K R, TINOCO E N, et al. Summary of data from the Fifth Computational Fluid Dynamics Drag Prediction Workshop [J]. Journal of Aircraft, 2014, 51(4): 1194-1213.
[15] TINOCO E N, BRODERSEN O, KEYE S, et al. Summary of data from the Sixth AIAA CFD Drag Prediction Workshop: CRM case 2 to 5: AIAA-2017-1208[R]. Reston,VA: AIAA, 2017.
[16] KEYE S, MAVRIPLIS D. Summary of data from the Sixth AIAA CFD Drag Prediction Workshop: Case 5 (coupled aero-structural simulation): AIAA-2017-1207[R]. Reston,VA: AIAA, 2017.
[17] RUMSEY C L, MORRISON J H, BIEDRON R T, et al. CFD variability for a civil transport aircraft near buffet-onset conditions: NASA/TM-2003-212149[R]. Washington, D.C.: NASA, 2003.
[18] SLOTNICK J, KHODADOUST A, ALONSO J, et al. CFD vision 2030 study: A path to revolutionary computational aerosciences: NASA/CR-2014-218178[R]. Washington, D.C.: NASA, 2014.
[19] VASSBERG J, DEHAAN M, SCLAFANI T. Grid generation requirements for accurate drag predictions based on OVERFLOW calculations: AIAA-2003-4124[R]. Reston, VA: AIAA, 2003.
[20] TINOCO E N, WINKLER C, MANI M, et al. Structured and unstructured solvers for the 3rd CFD Drag Prediction Workshop:AIAA-2007-0255[R]. Reston, VA: AIAA, 2007.
[21] MAVRIPLIS D J. Results from the 3rd Drag Prediction Workshop using the NSU3D unstructured mesh solver:AIAA-2007-0256[R]. Reston, VA: AIAA, 2007.
[22] SCLAFANI A J, VASSBERG J C, HARRISON N A, et al. Drag predictions for the DLR-F6 wing/body and DPW wings using CFL3D and OVERFLOW on an overset mesh: AIAA-2007-0257[R]. Reston, VA: AIAA, 2007.
[23] BRODERSEN O, EISFELD B, RADDATZ J, et al. DLR results from the Third AIAA CFD Drag Prediction Workshop: AIAA-2007-0259[R]. Reston, VA: AIAA, 2007.
[24] SCLAFANI A J, VASSBERG J C, RUMSEY C, et al. Drag prediction for the NASA CRM wing/body/tail using CFL3D and OVERFLOW on an overset Mesh: AIAA-2010-4219 [R]. Reston, VA: AIAA, 2010.
[25] TEMMERMAN L, HIRSCH C. Simulations of the CRM configuration on unstructured hexahedral grids: Lessons learned from the DPW-4 Workshop: AIAA-2010-4670[R]. Reston, VA: AIAA, 2010.
[26] VASSBERG J C. A unified baseline grid about the common research model wing-body for the Fifth AIAA CFD Drag Prediction Workshop: AIAA-2011-3508[R]. Reston, VA: AIAA, 2011.
[27] MARTINEAU D, STOKES S, MUNDAY S, et al. Anisotropic hybrid mesh generation for industrial RANS applications: AIAA-2006-0534[R]. Reston, VA: AIAA, 2006.
[28] DENG X G, ZHANG H X. Developing high-order weighted compact nonlinear schemes[J]. Journal of Computational Physics, 2000, 165: 24-44.
[29] DENG X G, MIN R B, MAO M L, et al. Further studies on geometric conservation law and application to high-order finite difference scheme with stationary grid[J]. Journal of Computational Physics, 2013, 239: 90-111.
[30] 王运涛, 孙岩, 王光学, 等. 高阶精度方法下的湍流生成项对跨声速流动数值模拟的影响研究[J].空气动力学学报,2015, 33(1): 25-30.
WANG Y T, SUN Y, WANG G X, et al. Numerical study of the effect of turbulent production terms on the simulation of transonic flows with high-order numerical method[J]. Acta Aerodynamica Sinica, 2015, 33(1): 25-30 (in Chinese).
[31] 王运涛, 孙岩, 王光学, 等. 湍流模型离散精度对数值模拟影响的计算分析[J]. 航空学报, 2015, 36(5): 1453-1459.
WANG Y T, SUN Y, WANG G X, et al. Numerical study of the effect of turbulent production terms on the simulation of transonic flows with high-order numerical method[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(5): 1453-1459 (in Chinese)
[32] 王运涛, 孙岩, 李松, 等. 高阶精度方法下的湍流生成项对低速流动数值模拟的影响研究[J]. 空气动力学学报, 2015,33(3): 325-329.
WANG Y T, SUN Y, LI S, et al. Numerical analysis of the effect of turbulent production terms in low-speed numerical simulation[J]. Acta Aerodynamica Sinica, 2015,33(3): 325-329 (in Chinese)
[33] 王运涛, 孙岩, 王光学, 等. DLR-F6翼身组合体的高阶精度数值模拟[J]. 航空学报, 2015, 36(9): 2923-2929.
WANG Y T, SUN Y, WANG G X, et al. High-order numerical simulation of DLR-F6 wing-body configuration[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(9): 2923-2929 (in Chinese).
[34] 王光学, 张玉伦, 王运涛, 等. BLU-SGS方法在WCNS高阶精度格式上的数值分析[J]. 空气动力学学报, 2015, 33(6):733-739.
WANG G X, ZHANG Y L, WANG Y T, et al. Numerical analysis of BLU_SGS method in WCNS high-order scheme[J]. Acta Aerodynamica Sinica, 2015, 33(6): 733-739 (in Chinese).
[35] 王运涛, 孟德虹, 孙岩, 等. DLR-F6/FX2B翼身组合体构型高阶精度数值模拟[J]. 航空学报, 2016, 37(2): 484-490.
WANG Y T, MENG D H, SUN Y, et al. High-order numerical simulation of DLR-F6/FX2B wing-body configuration[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 484-490 (in Chinese).
[36] 王运涛, 孙岩, 孟德虹, 等. CRM翼/身/平尾组合体模型高阶精度数值模拟[J]. 航空学报, 2016, 37(12): 3692-3697.
WANG Y T, SUN Y, MENG D H, et al. High-order numerical simulation of CRM wing/body/horizontal tail model[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(12): 3692-3697 (in Chinese).
[37] 王运涛, 孙岩, 孟德虹, 等. CRM翼身组合体模型高阶精度数值模拟[J]. 航空学报, 2017, 38(3): 120298.
WANG Y T, SUN Y, MENG D H, et al. High-order numerical simulation of CRM wing-body model[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(3): 120298 (in Chinese).
[38] 王运涛, 孟德虹, 孙岩, 等. CRM-WB风洞模型高阶精度数值模拟[J]. 航空学报, 2018, 39(4): 121642.
WANG Y T, MENG D H, SUN Y, et al. High-order numerical simulation of CRM-WB wind tunnel model[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(4): 121642 (in Chinese).
[39] ROY C J, RUMSEY C, TINOCO E N. Summary of data from the Sixth AIAA CFD Drag Prediction Workshop: Case 1 code verification[R]. Reston,VA: AIAA, 2017.
[40] SPALART P R, ALLMARAS S R. A one-equation turbulence model for aerodynamic flows: AIAA-1992-0439[R]. Reston,VA: AIAA, 1992.
[41] MENTER F R. Two-equation eddy-viscosity turbulence models for engineering application[J]. AIAA Journal, 1994, 32(8): 1598-1605.
[42] ANTON P S, JOHNSON D J, BLOCK M, et al. Wind tunnle and propulsion test facilities: Supporting analyses toan assessment of NASA’s capabilities to serve national needs: RAND_TR134[R]. California: RAND, 2004.
[43] SPALART P R. Strategies for turbulence modelling and simulations[J]. International Journal of Heat and Fluid Flow, 2000, 21: 252-263.
[44] YAMAMOTO K, TANAKA K, MURAYAMA M. Effect of a nonlinear constitutive relation for turbulence modeling on predicting flow separation at wing-body juncture of transonic commercial aircraft: AIAA-2012-2895[R]. Reston,VA: AIAA, 2012.
[45] OBERKAMPF W L, TRUCANOB T G. Verification and validation in computational fluid dynamics[J]. Progress in Aerospace Sciences, 2002, 38: 209-272.
[46] DAVID H U E. CFD investigation on the DPW-5 configuration with measured experimental wing twist using the elsA slover and the far-field approach:AIAA-2013-2508[R]. Reston,VA: AIAA, 2013.
[47] KEYE S, TOJITI V, EISFELD B, et al. Investigation of fluid-structure-coupling and turbulence model effects on the DLR results of the Fifth AIAA CFD Drag Prediction Workshop:AIAA-2013-2509[R]. Reston,VA:AIAA, 2013.
[48] KEYE S, BRODERSEN O, RIVERS M B, et al. Investigation of aeroelastic effects on the NASA common research model[J]. Journal of Aircraft, 2014, 51(4):1323-1330.
[49] MORRISON J H. Statistical analysis of the fifth drag prediction workshop computational fluid dynamics solutions[J]. Journal of Aircraft, 2014, 51(4):1214-1222.
[50] DERLAGA J M, MORRISONY J H. Statistical analysis of CFD solutions from the 6th AIAA CFD drag prediction workshop: AIAA-2017-1209[R]. Reston,VA: AIAA, 2017.
[51] RIVERS M B, HUNTER C A. Support system effects on the NASA common research model:AIAA-2012-0707[R]. Reston,VA: AIAA, 2012.
[52] RIVERS M B, HUNTER C A, CAMPBELL R L. Further investigation of the support system effects and wing twist on the NASA common research model:AIAA-2012-3209[R]. Reston,VA: AIAA, 2012.
[53] ZILLIAC G G, PULLIAM T H, RIVERS M B, et al. A comparison of the measured and computed skin friction distribution on the common research model:AIAA-2011-1129[R]. Reston,VA: AIAA, 2011.
[54] 王运涛, 孙岩, 孟德虹, 等. 包含支撑装置和机翼变形的CRM-WB模型气动特性数值模拟[J]. 航空学报, 2017, 38(12): 121202.
WANG Y T, SUN Y, MENG D H, et al. Numerical simulation of aerodynamic characteristics of CRM-WB model with support system and wing deformation[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(12): 121202 (in Chinese).
[55] 王运涛, 王光学, 张玉伦. 采用TRIP2.0软件计算DLR-F6构型的阻力[J]. 空气动力学学报, 2009, 27(1): 108-111.
WANG Y T, WANG G X, ZHANG Y L. Drag prediction of DLR-F6 configuration with TRIP2.0 software[J]. Acta Aerodynamica Sinica, 2009, 27(1): 108-111 (in Chinese).
[56] 王运涛, 王光学, 张玉伦. DPW Ⅲ机翼和翼身组合体构型数值模拟[J]. 空气动力学学报, 2011, 29(3): 264-269.
WANG Y T, WANG G X, ZHANG Y L. Numerical simulation of DPW Ⅲ wing and wing-body configurations[J]. Acta Aerodynamica Sinica, 2011, 29(3): 264-269 (in Chinese).
[57] OWENS L R, WAHLS R A, RIVERS S M. Off-design Reynolds number effects for a supersonic transport[J]. Journal of Aircraft, 2005, 42(6): 1427-1441.
[58] KEYE S, RUDNIK R. Aero-elastic simulation of DLR’s F6 transport aircraft configuration and comparison to experimental data: AIAA-2009-0580[R]. Reston, VA:AIAA, 2009.
[59] MOUTON S, SANT Y L, LYONNET M. Prediction of the aerodynamic effect of model deformation during transonic wind tunnel tests[J]. International Journal of Engineering Systems Modelling and Simulation, 2013, 5(1-3): 44-56.
[60] HEEG J, CHWALOWSKI P, FLORANCE J P, et al. Overview of the aeroelastic predication workshop: AIAA-2013-0783[R]. Reston, VA: AIAA, 2013.
[61] LYU Z J, KENWAY G K W, MARTINS J R R A. RANS-based aerodynamic shape optimization investigations of the common research model wing: AIAA-2014-0567[R]. Reston, VA: AIAA, 2014.
[62] KENWAY G K W, MARTINS J R R A. Aerodynamic shape optimization of the CRM configuration including buffet-onset conditions: AIAA-2016-1294[R]. Reston, VA: AIAA, 2016.
[63] 陈颂, 白俊强, 史亚云, 等. 民用客机机翼/机身/平尾构型气动外形优化设计[J]. 航空学报, 2015, 36(10): 3195-3207.
CHEN S, BAI J Q, SHI Y Y, et al. Aerodynamic shape optimization design of civil jet wing-body-tail configuration[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(10): 3195-3207 (in Chinese).
[64] 刘峰博, 郝海兵, 李典, 等. 离散伴随方法在气动优化设计中的应用[J]. 航空计算技术, 2017, 42(2): 33-40.
LIU F B, HAO H B, LI D, et al. Application of discrete adjoint method in aerodynamic shape optimization design[J]. Aeronautical Computing Technique, 2017, 42(2): 33-40 (in Chinese).
[65] LIEM R P, KENWAY G K W, MARTINS J R R A. Multi-point, multi-mission, high-fidelity aerostructural optimization of a long-range aircraft configuration: AIAA-2012-5706[R]. Reston, VA: AIAA, 2012.
[66] GAETAN K W, KENWAY G K W, MARTINS J R R A. Multipoint high-fidelity aerostructural optimization of a transport aircraft configuration[J]. Journal of Aircraft, 2014, 51(1): 144-160.

