脉冲射流冲击平直表面的对流换热实验
吕元伟,张靖周, 2, *,唐婵,单勇
1.南京航空航天大学 能源与动力学院 江苏省航空动力系统重点实验室,南京 210016 2.先进航空发动机协同创新中心,北京 100083
射流冲击是强化局部换热的一种有效技术途径,在动力装置热端部件强化冷却、飞行器表面热气防冰、电子器件高效散热等许多技术领域得到广泛应用[1-3]。
长期以来,射流冲击强化传热一直是国内外研究人员关注的研究课题,尤其是20世纪80年代以来,为适应高新科学技术发展所带来的日益增长的高效传热需求,研究人员更加注重射流冲击强化措施的创新研究[4],发展了一系列被动(如异型喷嘴、处理靶面和涡激励等[5-9])或主动(如基于机械间断、声学或电磁效应等方式形成的脉冲射流和合成射流[10-14])的强化传热技术措施。与连续射流冲击相比,非稳定脉冲射流在冲击换热的机制上更为复杂,由于脉冲射流具有的脉动特征,一方面增强了射流湍流强度,周期性地破坏热边界层;另一方面,导致射流与周围流体掺混加剧,使射流核心区速度降低,因此脉冲射流相对于稳定连续射流冲击能否形成换热增强效果,与射流固有的脉冲特征(波形、频率、幅值)以及射流时均雷诺数、射流冲击间距等密切相关。Sheriff和Zumbrunnen[15]提出了用无量纲的斯特劳哈尔数(Sr=fD/um,f为脉冲频率,D为喷管直径,um为射流平均速度)来评判脉冲射流与连续射流对冲击靶板换热的影响,其研究表明在较小的斯特劳哈尔数范围内(0.012≤Sr≤0.144),脉冲射流相对连续射流的对流换热系数相对降低17%,而在较高的斯特劳哈尔数下(Sr=0.51)则相对增强33%。然而针对不同的射流雷诺数和脉冲频率范围,临界斯特劳哈尔数却并不相同[16-18],尤其是对于冲击间距的影响,甚至出现截然相反的结果,譬如,Hofmann等[19]利用高速电磁阀激励的脉冲射流冲击换热实验表明(时均射流雷诺数Re范围为14 000~78 000,2 Hz≤f≤400 Hz),在小冲击间距比(H/D=2,H为射流管到耙板的距离)下,脉冲射流驻点对流换热系数增强最为明显,而在大间距比和很小的斯特劳哈尔数下则呈现换热下降的趋势。Behera等[20]研究了25 Hz≤f≤400 Hz(对应于0.008≤Sr≤0.13)、5≤H/D≤9时的脉冲射流冲击换热,发现即便在较小的斯特劳哈尔数下脉冲射流依然具有高于连续射流的对流换热系数。Persoons等[21]通过系统的实验,研究了6 000≤Re≤14 000、9 Hz≤f≤55 Hz的脉冲射流冲击换热,指出当Sr(H/D)>0.1时脉冲射流相对于连续射流具有更强的对流换热能力。
脉冲射流冲击换热的影响因素众多,对此,本文通过实验研究脉冲射流冲击平直表面的对流换热特性,并进一步阐明其与连续射流换热性能差异的主导因素。
1 实验描述
1.1 实验系统
脉冲射流冲击换热实验系统如图1所示。冲击射流由小型空气压缩机提供,经过调节阀和流量控制器进入脉冲射流激励装置,脉冲射流由电磁阀激励形成,通过信号发生器对电磁阀两端的电压占空比进行控制,进而得到按照特定规律周期性变化的脉冲射流。本文实验中,射流管直径D=10 mm,长径比L/D=12(L为射流管长度)。
图2为时均射流雷诺数Re=10 000工况下,运用热线风速仪测试获得的喷管出口中心位置(H/D=0)上,脉冲射流占空比A=50%、脉冲频率f=10 Hz时的脉冲射流速度随时间的变化,图中T为脉冲射流周期。对于连续射流,喷管出口的速度也存在非常微弱的变化,但总体可以视为是连续稳定的;对于脉冲射流,在电磁阀开通的值班周期内射流的速度为连续性射流速度的2倍,处于电磁阀闭合的周期间隔内孔口出口中心位置的速度接近1 m/s,这是由于射流管内的气流惯性所致。总体而言,本文的实验装置能够产生满足要求的脉冲射流。
在射流冲击换热实验中,将加热膜固定在圆形铜棒上,铜棒两端施加电压,热膜加热的热流由直流稳压电源提供。为了使得热膜表面平整,在热膜两端施加一定的张紧力,加热表面温度由红外热像仪测量。本文研究中,脉冲射流的频率和占空比分别恒定为10 Hz和50%,改变射流的雷诺数和冲击间距,主要实验参数列于表1。

图1 脉冲射流冲击换热实验系统示意图Fig.1 Schematic of experimental system of pulsed jet impingement heat transfer

图2 喷管出口脉冲射流速度随时间的变化Fig.2 Variation of velocity of pulsed jet at nozzle outlet with time
表1 主要实验参数Table 1 Main experimental parameters

ParameterValueRe5000,10000,20000D/mm10L/mm120f/Hz10A/%50H/D2,4,6,8
1.2 实验测试和数据处理
加热表面温度采用工作波段为8~14 μm的红外热像仪测试,为保障红外测温精度,将加热表面预先均匀地喷涂黑漆[22-23],标定实验结果表明测试表面的发射率约为0.96。


图3 加热表面热流平衡模型示意图Fig.3 Schematic of heat balance model on heater foil

图4 加热表面散热损失预测实验Fig.4 Pre-test for estimating heat loss on heater foil
加热表面背侧的热流损失通过预先进行的标定实验加以预测,如图4(a)所示,即将加热膜放置于厚度δ3=30 mm的绝热石棉板上,用厚度δ1=0.5 mm的铜板压紧在加热膜(厚度为δ2)上,通过调节加热膜的输入电流,得到不同加热热流密度下的表面温度,由能量方程可知,显然上述测试得到的散热损失来源于表面的自然对流以及辐射换热。即
(1)
式中:heff,b为计及自然对流和辐射散热的当量对流换热系数;Tb为热膜表面温度;Ta为环境温度。
图4(b)为实验测得的表面当量对流换热系数随表面和环境温度差的变化,在本文研究的温度差范围内基本呈现线形变化的趋势,拟合得到热膜上表面的当量对流换热系数heff,b(单位为W/(m2·K))为
heff,b=0.11(Tb-Ta)+12
(2)
加热膜射流冲击侧与环境之间的辐射换热量可以近似处理为
(3)
式中:Tw和εw分别为加热膜表面温度和发射率;σ为Stefan-Boltzmann常数。
由此,射流冲击的局部对流换热系数为
(4)
式中:Tj为冲击射流温度,在低的射流速度下,冲击射流的静温与其总温可视为相同,由喷管出口处的温度探针测得。
理论上,脉冲射流作用下壁面温度呈现出周期性的变化规律。但是当经历了一定的周期后,壁面上的温度趋于准稳定状态,即在一个周期内壁面温度变化极其微弱。定义射流冲击局部努塞尔数Nu为
(5)
式中:k为射流的导热系数。
本文引入了两种平均方式来确定射流冲击平均努塞尔数,即
1) 周向平均,取射流驻点径向位置处的周向值进行平均,记为NuL-Average。
2) 局部区域平均,沿射流驻点径向位置包络的区域进行平均,记为NuR-Average。
实验测试中,所有实验数据的重复度为2.5%。本实验中质量流量控制器的精度为3.3%;考虑辐射和自然对流带来热损失时,平板当量热流密度qtarget计算比较复杂,本实验精度设定为5%;射流温度Tj和环境温度Ta由K型热电偶测得,精度为±0.5 ℃;平板表面的温度Tw由红外热像仪获得,精度为±2%|t|(|t|为热像仪获得的测量温度与环境温度的差值)。同时,喷嘴出口直径D的测量不确定度为1%。考虑到温度的变化引起流体热物性的变化,由误差传递函数[24],可得靶板表面的努塞尔数误差为5.5%。射流雷诺数的误差为7.5%。
1.3 实验方法验证
Violato等[25]得到了Re=10 000工况,不同冲击间距比H/D下表面周向平均努塞尔数NuL-Average沿R/D的分布规律(误差小于3.5%),本文参考Violato等的稳定射流冲击实验工况进行了实验方法验证,实验中R为以滞止中心位置为原点时拾取区域的半径。图5为本文实验获得的平板表面努塞尔数和Violato等的实验数据比较。可以看出,在H/D=2、4时,本文得到的射流驻点附近的努塞尔数略高于Violato等的实验数据,而在H/D=8时,本文的实验结果略低于Violato等的实验数据。但是在R/D>1.5后,本文的实验结果与Violato等的实验数据吻合良好,两者的最大误差在7%以内。

图5 本文实验结果与Violato等[25]的比较Fig.5 Comparison between current experimental results and results obtained by Violato et al.[25]
2 实验结果与分析
2.1 努塞尔数径向分布
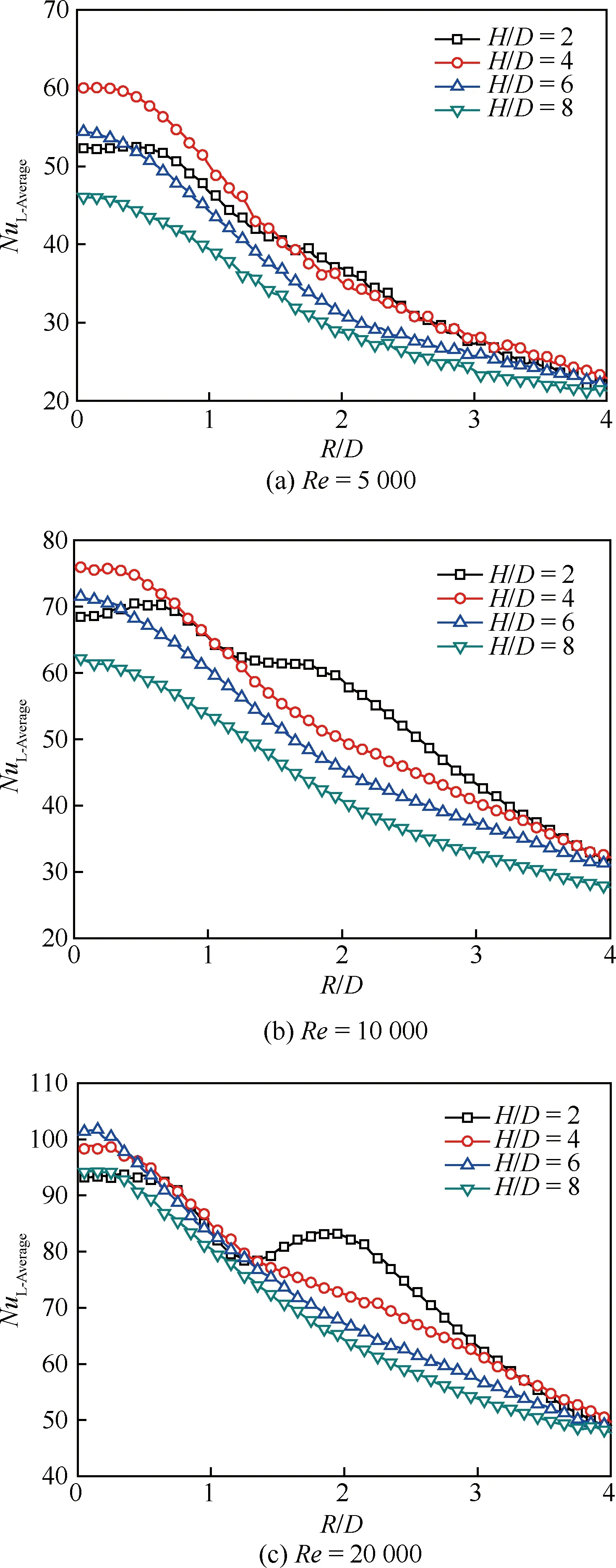
图6 连续射流冲击时平板表面的周向平均 努塞尔数沿径向的分布 Fig.6 Distribution of line-averaged Nusselt number on plate surface along radial direction for continuous jet impingement
图6为连续性射流冲击时平板表面的周向平均努塞尔数NuL-Average沿径向的分布规律。随着射流雷诺数的增加,射流冲击周向平均努塞尔数呈现持续增大的趋势;在Re=5 000和Re=10 000工况下,射流驻点区的周向平均努塞尔数在射流冲击间距比H/D=4最高,在Re=20 000工况下,射流驻点区的周向平均努塞尔数换热最大值则出现在H/D=6的射流冲击间距比。同时射流冲击周向平均努塞尔数沿径向基本呈现急剧降低的变化趋势,这是驻点区射流法向冲击壁面形成壁面射流的作用特征,但在小的射流冲击间距比H/D=2时,NuL-Average在R/D=2径向位置处呈现第2个峰值,这是因为在小的射流冲击间距下,射流趋赴壁面的速度高,从而对近驻点区的壁面射流形成强烈的扰动,使得局部对流换热能力提高。

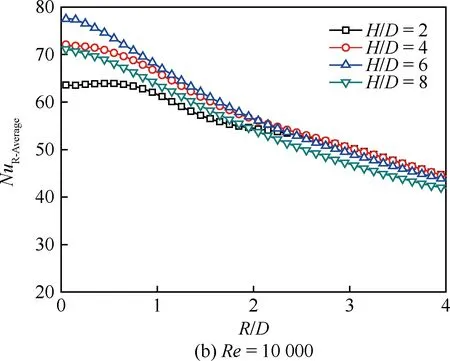
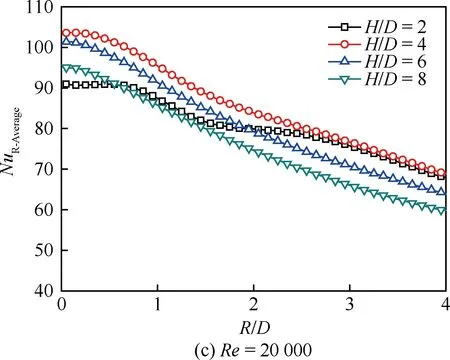
图7 f=10 Hz的脉冲射流冲击时平板表面的周向 平均努塞尔数沿径向的分布 Fig.7 Distribution of line-averaged Nusselt number on plate surface along radial direction for pulsed jet impingement with f=10 Hz
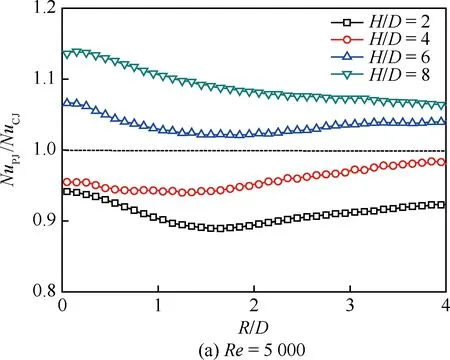
图7为f=10 Hz的脉冲射流冲击时平板表面的周向平均努塞尔数NuL-Average沿径向的分布规律。与连续射流冲击相比,可以看出脉冲射流冲击的周向平均努塞尔数依然具有随射流雷诺数增加而提高、沿径向急剧降低等基本特征,但是注意到脉冲射流冲击将引起若干差异。在大射流冲击间距比下(H/D=8),脉冲射流在射流驻点区对流换热能力较连续射流有所提高,在雷诺数较小的工况下体现尤为明显;而在小射流冲击间距比下(H/D=2),脉冲射流在射流驻点区对流换热能力则弱于连续射流。对于偏离射流驻点区的壁面射流区,脉冲射流也呈现较为复杂的影响规律,譬如,在Re=5 000时,H/D=4下的脉冲射流虽然在驻点区的对流换热弱于连续射流,但其在壁面射流区2 图8 f=10 Hz的脉冲射流冲击时平板表面的局部 区域平均努塞尔数沿径向的分布 Fig.8 Distribution of local region-averaged Nusselt number on plate surface along radial direction for pulsed jet impingement with f=10 Hz 图8为f=10 Hz的脉冲射流冲击时平板表面的局部区域平均努塞尔数NuR-Average沿径向的分布规律。若以一倍射流管直径作为圆形区域半径进行平均,脉冲射流的局部区域平均努塞尔数均在H/D=4和H/D=6时较优,H/D=2时最低;然而,若以2~4倍射流管直径作为圆形区域半径进行平均,则在H/D=4和H/D=2时相对较优,H/D=8时最低。在本文所研究的特定脉冲激励方式下,H/D=4是相对较优的冲击间距比。 鉴于射流冲击局部强化传热的特点,以局部区域平均作为对比基准评价脉冲射流相对连续射流的冲击换热效果,即采用脉冲射流局部区域平均的努塞尔数NuPJ与连续性射流局部区域平均的努塞尔数NuCJ之比进行表示。图9反映了典型射流雷诺数下冲击间距的影响。 图9 基于局部区域平均方式的H/D对 NuPJ/NuCJ的影响Fig.9 Effect of H/D on NuPJ/NuCJbased on local region-averaged mode 由图9可以看出,在Re=5 000时,射流冲击间距比H/D=6和H/D=8下的脉冲射流较连续射流可以获得更好的强化换热效果;随着射流雷诺数的增加,H/D=4下的脉冲射流较连续射流也逐渐显示出传热强化的效果,在Re=20 000下脉冲射流的区域平均努塞尔数可以相对提高15%~20%;但在H/D=2时,基本都是以连续射流冲击为优,即便在Re=20 000下,仅当以3倍射流管直径作为区域半径进行平均时,脉冲射流才具有略高于连续射流冲击换热的作用效果。 本文通过实验,研究了脉冲频率为10 Hz、占空比为50%的脉冲射流冲击平板的对流换热,在射流雷诺数为5 000~20 000、冲击间距比为2~8范围内与相同工况下的连续射流进行了比较分析。主要结论如下: 1) 脉冲射流冲击的努塞尔数依然具有随射流雷诺数增加而提高、沿径向急剧降低等基本特征,但是与连续射流相比,脉冲射流冲击会引起射流驻点和壁面射流区的对流换热差异,其影响与射流雷诺数和射流冲击间距密切相关。 2) 以局部区域平均作为对比基准评价脉冲射流相对连续射流的冲击换热效果,在大的射流冲击间距比下(H/D=6、8),脉冲射流体现出传热增强的效果,而在小的射流冲击间距比下(H/D=2),连续射流更具优势。 3)Re=20 000工况下,仅当以3倍以上射流管直径作为区域半径进行平均时,脉冲射流才具有略高于连续射流冲击换热的作用效果。 [1] VISKANTA R. Heat transfer to impinging isothermal gas and flame jets[J]. Experimental Thermal and Fluid Science, 1993, 6(2): 111-134. [2] BUNKER R S. Gas turbine heat transfer: Ten remaining hot gas path challenges[J]. ASME Journal of Turbomachinery, 2007, 129(2): 193-210. [3] FREGEAU M, GABR M, PARASCHIVOIU I, et al. Simulation of heat transfer from hot-air jets impinging a three-dimensional concave surface[J]. Journal of Aircraft, 2009, 46(2): 721-725. [4] CARLOMAGNO G M, IANIRO A. Thermo-fluid-dynamics of submerged jets impinging at short nozzle-to-plate distance: A review[J]. Experimental Thermal and Fluid Science, 2014, 58: 15-35. [5] COLUCCI D W, VISKANTA R. Effect of nozzle geometry on local convective heat transfer to a confined impinging air jet[J]. Experimental Thermal and Fluid Science, 1996, 13(1): 71-80. [6] NAKOD P M, PRABHU S V, VEDULA R P. Heat transfer augmentation between impinging circular air jet and flat plate using finned surfaces and vortex generators[J]. Experimental Thermal and Fluid Science, 2008, 32(5): 1168-1187. [7] YANG H Q, KIM T, LU T J, et al. Flow structure, wall pressure and heat transfer characteristics of impinging annular jet with/without steady swirling[J]. International Journal of Heat and Mass Transfer, 2010, 53(19): 4092-4100. [8] VIOLATO D, SCARANO F. Three-dimensional evolution of flow structures in transitional circular and chevron jets[J]. Physics of Fluids, 2011, 23(12): 124104. [9] YU Y Z, ZHANG J Z, XU H S. Convective heat transfer by a row of confined air jets from round holes equipped with triangular tabs[J]. International Journal of Heat and Mass Transfer, 2014, 72: 222-233. [10] ZUMBRUNNEN D A, AZIZ M. Convective heat transfer enhancement due to intermittency in an impinging jet[J]. ASME Journal of Heat Transfer, 1993, 115(1): 91-98. [11] 周静伟, 杨兴贤, 耿丽萍, 等. 非稳态冲击射流强化传热试验研究[J]. 机械工程学报, 2010, 46(6): 144-148. ZHOU J W, YANG X X, GENG L P, et al. Experimental investigation on heat transfer augmentation with unsteady impinging jet[J]. Journal of Mechanical Engineering, 2010, 46(6): 144-148 (in Chinese). [12] ZHOU J W, WANG Y G, MIDDELBERG G, et al. Unsteady jet impingement heat transfer on smooth and non-smooth surfaces[J]. International Communications in Heat and Mass Transfer, 2009, 36(2): 103-110. [13] VALIORGUE P, PERSOONS T, MCGUINN A, et al. Heat transfer mechanisms in an impinging synthetic jet for a small jet-to-surface spacing[J]. Experimental Thermal and Fluid Science, 2009, 33(4): 597-603. [14] ZHANG J Z, GAO S, TAN X M. Convective heat transfer on a flat plate subjected to normally synthetic jet and horizontally forced flow[J]. International Journal of Heat and Mass Transfer, 2013, 57(1): 321-330. [15] SHERIFF H, ZUMBRUNNEN D. Effect of flow pulsations on the cooling effectiveness of an impinging jet[J]. ASME Journal of Heat Transfer, 1994, 116(4): 886-895. [16] HERWIG H, MIDDELBERG G. The physics of unsteady jet impingement and its heat transfer performance[J]. Acta Mechanics, 2008, 201(1): 171-184. [17] MEDINA H, BENARD E, EARLY J M. Reynolds number effects on fully developed pulsed jets impinging on flat surfaces[J]. AIAA Journal, 2013, 51(10): 2305-2318. [18] ALIMOHAMMADI S, MURRAY D B, PERSOONS T. On the numerical-experimental analysis and scaling of convective heat transfer to pulsating impinging jets[J]. International Journal of Thermal Sciences, 2015, 98: 296-311. [19] HOFMANN H T, MOVILEANU D L, KIND M, et al. Influence of a pulsation on heat transfer and flow structure in submerged impinging jets[J]. International Journal of Heat and Mass Transfer, 2007, 50(17-18): 3638-3648. [20] BEHERA R C, DUTTA P, SRINIVASAN K. Numerical study of interrupted impinging jets for cooling of electronics[J]. IEEE Transactions on Components and Packaging Technologies, 2007, 30(2): 275-284. [21] PERSOONS T, BALGAZIN K, BROWN K, et al. Scaling of convective heat transfer enhancement due to flow pulsation in an axisymmetric impinging jet[J]. ASME Journal of Heat Transfer, 2013, 135(11): 111012. [22] TAN X M, ZHANG J Z. Flow and heat transfer characteristics under synthetic jets impingement driven by piezoelectric actuator [J]. Experimental Thermal and Fluid Science, 2013, 48: 134-146. [23] 李鑫郡, 张靖周, 谭晓茗. 单个压电风扇传热特性研究[J]. 航空学报, 2017, 38(7): 120982. LI X J, ZHANG J Z, TAN X M. Characteristics of heat transfer with a single piezoelectric fan[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(7): 120982 (in chinese). [24] MOFFAT R J. Describing the uncertainties in experimental results[J]. Experimental Thermal and Fluid Science, 1998, 1(1): 3-17. [25] VIOLATO D, IANIRO A, CARDONE G, et al. Three-dimensional vortex dynamics and convective heat transfer in circular and chevron impinging jets[J]. International Journal of Heat and Fluid Flow, 2012, 37: 22-36.
2.2 脉冲射流与连续射流冲击换热的比较


3 结 论

