不同形式地下轨道动力特性及减振性能研究

唐 娟

(合肥铁路工程学校，安徽 合肥 230000)

0 引言

本文基于ANSYS，分别建立了地下常用轨道形式计算模型；列车荷载通过车辆简化模型模拟；分别从隧道梁自振特性和时频域的角度分析各类轨道的减振效果。

1 计算模型及参数

1.1 列车荷载的模拟

本文采用地铁B型车，6节编组，单节车辆的轴距与定距为2.2 m，12.6 m。由于地铁车辆重心在纵横向都是对称的，将其竖向振动简化为单自由度模型如图1a)所示。该轮系以速度V在不平顺的轨道上行驶，轮轨间相互作用力为P(t)。模型中参数：1/8车体质量Mc=7 040 kg，1/2轮对质量Mw=750 kg、集总刚度K=0.79 kN/mm、集总阻尼C=32.7 kNs/m，其中，yc为车体振动位移；yw为车轮振动位移并假设为系统的外界激励。

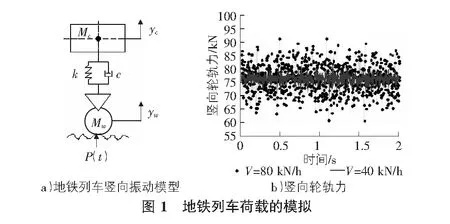
文中采用德国低干扰谱来模拟轨道不平顺状态，波长范围取1.524 m～304.8 m，时间步长dt=0.002 5 s，车速分别取40 km/h，80 km/h。数定力采用三角级数法模拟，计算结果如图1b)所示，该数定力可以反映不平顺和车速的影响。

1.2 轨道—隧道梁—土体模型

基于ANSYS的不同轨道形式采用梁、质点、弹簧的模拟方法，分为整体道床、弹性短轨枕、橡胶支承浮置板轨道、钢弹簧浮置板轨道四种工况。谐响应分析轨道长取60 m，瞬态分析时轨道长取180 m。工况3、工况4的道床宽3.2 m、厚0.4 m。隧道梁截面参数通过ANSYS获取截面信息所得，各工况轨道模型中钢轨为CHN60；扣件型号为DTV12，刚度k=30 kN/mm、阻尼c=75 kNs/m；弹性短轨枕轨道，轨枕质量M=111.4 kg、轨下支承刚度k=25 kN/mm、阻尼c=75 kNs/m；浮置板轨道，轨道板弹性模量3.3×1010N/m2、密度ρ=2 500 kg/m3，其中橡胶支承刚度k=20 kN/mm、阻尼c=75 kNs/m，弹簧支承刚度k=6.9 kN/mm、阻尼c=75 kNs/m；基础梁弹性模量E=2.85×1010N/m2、密度ρ=2 500 kg/m3；土体刚度k=5.3×103kN/mm、损耗因子η=0.03。

2 扫频分析

文中采用该法定量分析不同轨道形式在0 Hz～200 Hz内所有共振频率对力的传递力的影响大小。为了判断轨道—隧道土体这一复杂体系中各部件的作用，共设计了三个计算模型：1)不考虑隧道土体的模型；2)考虑隧道土体的模型；3)改变工况4模型的土体刚度来判断土质的作用(ζ为土体刚度比例系数)。加载时，加载节点为跨中钢轨节点、力的幅值F=1 kN、频率范围取0 Hz～200 Hz。文中采用力的传递率LT作为指标判断系统的隔振效果，其定义如下式：

LT=20×log(∑fi/F)(i=底部约束节点数)。

式中：fi——底部约束节点的竖向反力；

F——加载力，1 kN。

根据图2可知：

1)不考虑隧道土体时可以判断各轨道形式的最不利共振点及工作频段：一方面轨道的基频决定其工作频段，工况4的工作频段最宽且单点最大共振反力也最小；另一方面轨道的振型特性决定了线路方向内反力的波动特性，0 Hz～200 Hz工况4于工作频域的波动性使得单点的反力大大降低，但同时也使远处轨道发生振动，表现在讨论总反力的隔振效果时对于中高频的隔振效果不佳。

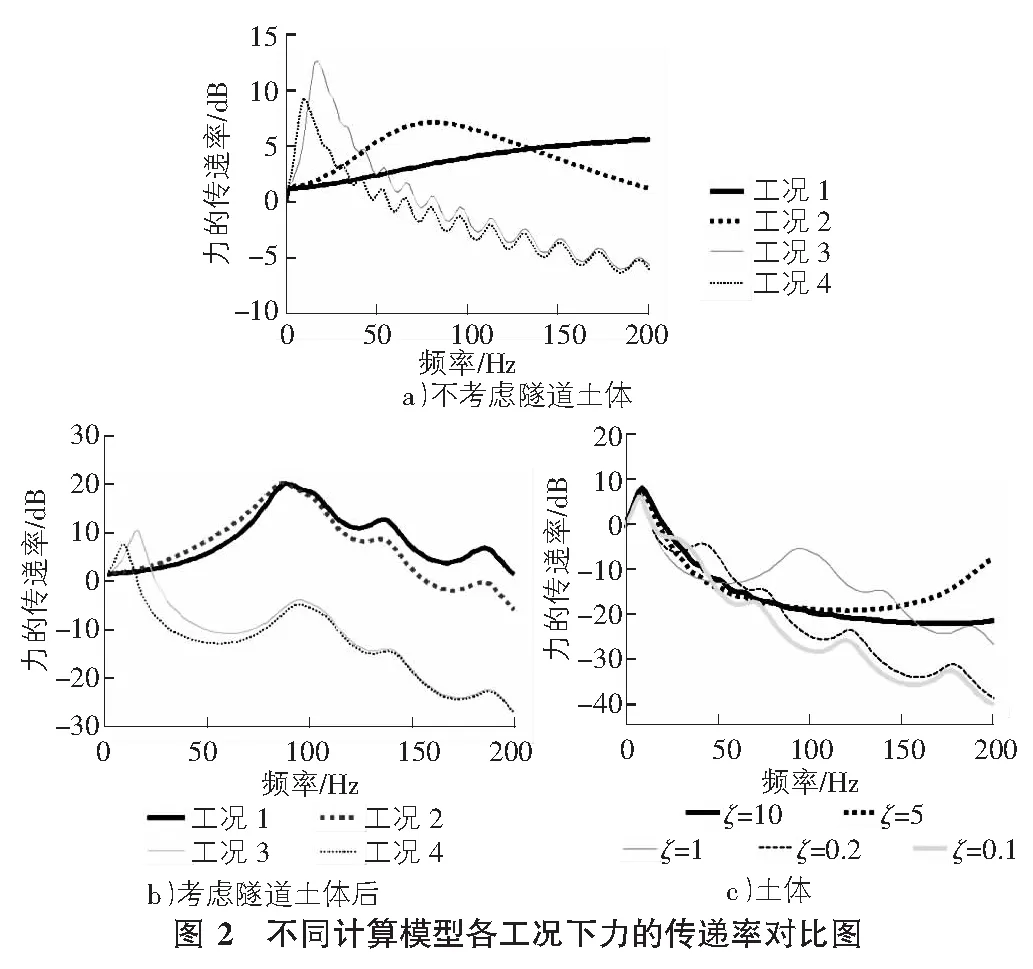
2)考虑隧道土体时，传递力的频域分布同时受到轨道与隧道梁的影响：一方面表现在共振频率上；另一方面表现在中高频力的传递率。

3)土体刚度决定了隧道梁的共振主频及振型的波动性，土体刚度越小对跨过隧道梁基频后的频段力的衰减更快。

3 瞬态分析

瞬态分析时考虑三种因素的影响：

1)由模型B得出轨道形式的影响(V=80 km/h)；2)由模型C得出土体刚度的影响(V=80 km/h)；3)由模型B中的钢弹簧浮置板轨道模型确定车速的影响(V=40 km/h～80 km/h)。上述模型中时间步长dt=0.002 5 s，取各轨道跨中部件节点为观察点。上述不同工况下隧道梁振动的频域分布见图3。

根据图3可知：

1)随机荷载下不同轨道形式隧道振动的频域分布走势大致相同，各轨道对应的主频皆为隧道梁的基频，可见隧道梁对整个减振系统传递到大地的振动影响较大；以整体道床为参考，其他各轨道表现的频域内差异大致可用图3b)解释，在靠近轨道基频范围内的隔振效果略差，跨过基频后振动衰减；弹性短轨枕的工作频率在100 Hz以上且100 Hz以内的隔振效果要差于整体道床，钢弹簧浮置板在10 Hz～50 Hz的隔振效果要优于橡胶支承浮置板轨道；各轨道的不利频段内的放大现象影响不大。

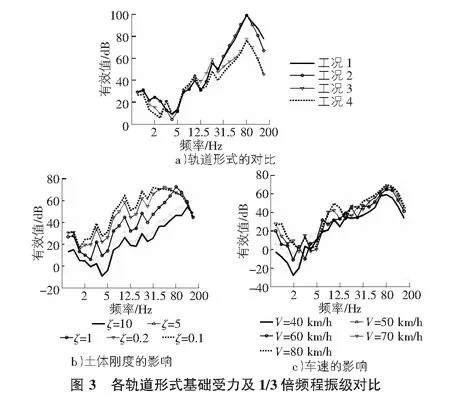
2)随机荷载下不同土质同样决定了隧道梁的振动分布：一方面，土体刚度越大隧道梁的振动越小，0 Hz～200 Hz内振动分布几乎整体下移；另一方面，不同土体刚度的隧道梁振动主频也对应其隧道梁的基频。

3)随机荷载下不同车速引起隧道梁振动分布走势大致相同，基本上各频道内车速越大有效振级越大。

4 结语

不同轨道形式下轨道自身的振动特性直接影响到隧道的振动，使得隧道梁的波动特性的阵型幅值及激发频率不同，钢弹簧浮置板轨道所需的激发频率最小且同阶振型幅值最小。不同的土质对轨道的振动影响不大但决定了隧道的振动，一方面影响隧道的振级大小，另一方面影响隧道振动频域内的主频分布。

参考文献：

[1] 耿传智,楼梦麟.浮置板轨道结构系统振动模态分析[J].同济大学学报(自然科学版),2006,9(34):1201-1205.

[2] 陈小平,王 平.弹性支承块式无砟轨道的减振原理[J].铁道学报,2007,5(29):69-72.

[3] 郭亚娟.列车振动荷载作用下地铁浮置板轨道动力特性分析[D].石家庄:石家庄铁道大学,2005.