基于PSO-SVR气膜薄壳钢筋混凝土结构的成本预测

王 荣 华

(河北工程大学土木工程学院，河北 邯郸 056038)

0 引言

气膜薄壳钢筋混凝土结构由欧美国家引入我国的建筑行业，由于它优良性能，结构形式美观，近年来作为一种新型大跨度空间结构形式被应用于工业建筑和民用建筑如煤炭、肥料、粮食等储仓和别墅、场馆、办公楼等。作为一种新型且受力性能良好的结构形式，它的成本问题必然是人们关注的重点。鉴于相关工程数据不足，经验有限，成本的研究及预测很有意义。

成本预测是用成本的数据及历史资料，推断未来项目的成本、费用及发展趋势。成本预测的关键问题是选择恰当的预测方法并建立数学模型，其方法:1)定性预测有专家会议法、主观概率法、德尔菲法等；2)定量方法有移动平均法、回归分析法等。严静[1]考虑企业运营成本统计方面的不确定性因素,提出了一种改进灰色预测模型。李万庆，陈明欣[2]提出一种鸡群算法CSO和支持向量回归机SVR结合模型对施工成本数据进行预测仿真。随着计算机智能算法的发展，将更多的应用于成本预测。由于启发式算法(遗传算法、蚁群算法等)具有的鲁棒性和通用性，可用做SVR模型参数寻优。本文用粒子群算法对SVR进行优化，得到含最佳参数的全局解，应用于预测模型。对气膜薄壳钢筋混凝土结构的施工成本数据进行预测。

1 气膜薄壳钢筋混凝土结构特点

1.1 结构施工特点

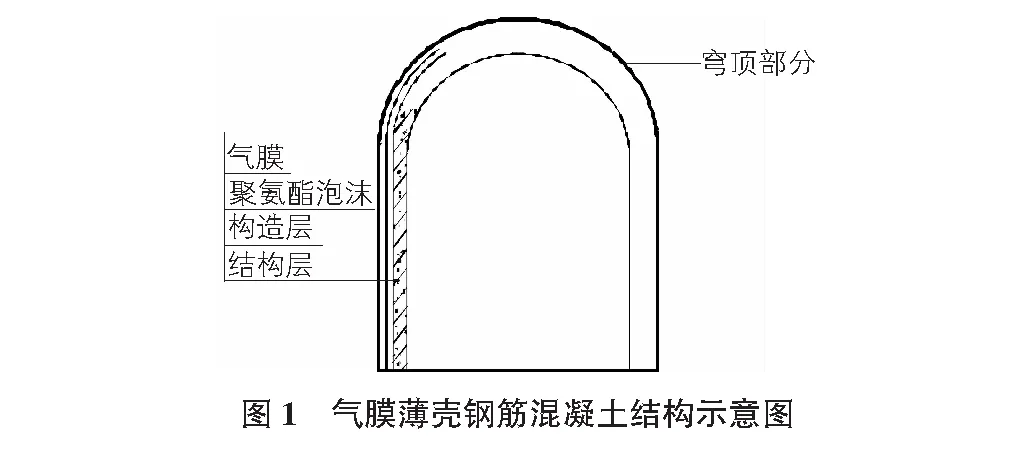
气膜薄壳钢筋混凝土结构示意图如图1所示，气膜薄壳钢筋混凝土结构以性能优良的柔软织物作为外膜，将加工好的外模固定在环形基础上，向膜内持续输入空气并保持恒压，随后在膜内喷涂聚氨酯泡沫层，然后再分层绑扎钢筋和喷射混凝土。

1)气膜分项：气膜的膜材是一种复合材料，由高强度纤维织成的基材和聚合物涂层构成，根据设计对膜材放样、裁剪、热合焊接形成空间曲面膜体，定型气膜充气后作为外模板(永久保留不拆除)，替代传统的脚手架等作为施工过程中的支撑系统，取代传统的木、钢模板。

2)聚氨酯泡沫层：工程做法是在气膜分项的施工质量验收合格基础上，球膜表面的干燥度检查合格后，在球仓气膜的表面滚涂或喷涂胶粘剂，然后再喷涂聚氨酯泡沫。该层可用作保温层。

3)钢筋混凝土：构造层由一层钢筋网片和喷射混凝土组成，结构层是由多层钢筋以及混凝土构成。球仓按1 m/圈～2 m/圈划分施工段，下层的混凝土厚度应保证上层混凝土厚度的2倍以上。气膜球仓顶部的混凝土，应沿竖向钢筋和水平钢筋采取隔一喷一，当将钢筋完全覆盖并形成骨架后可整体喷射混凝土。

1.2 施工工艺流程

环梁以下孔洞封堵、基础回填→球膜充气施工→聚氨酯喷涂→结构钢筋绑扎→喷射混凝土→球仓顶部开孔，下部开门[4]→主体完成。

2 粒子群算法优化支持向量机模型

2.1 支持向量机

SVM可以解决非线性、小样本和高维模式识别，把它用到函数的预测回归中，称为支持向量回归机(Suport Vecto Rmachine,SVR)。支持向量回归机利用核函数将低维空间线性不可分的问题通过非线性映射到高维空间实现高维空间的线性可分，再回归到低维实现低维空间线性可分。数据集T={(xi,yi),i=1,2,…,l}，(xi,yi)是样本的输入输出对。用其构造的回归函数为：

f(x)=ωTφ(x)+b

(1)

其中，ω为权值向量；φ(x)为数据变换到高维特征空间的非线性映射；b为阈值。引进了下面的结构风险函数：

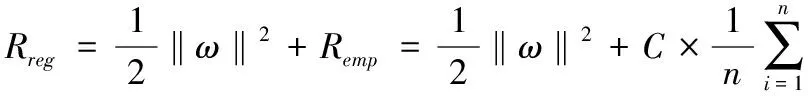
(2)

其中，‖ω‖2为描述函数；f(xi)为杂度的项；C为惩罚参数；∣yi-f(xi)∣为ε不敏感损失函数。

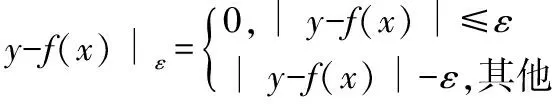
(3)

上述函数回归问题等价于最小化代价泛函：

s.t.

(4)

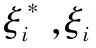
(5)

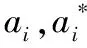
(6)

其中,σ为方差。将式(6)代入到式(5)中，最后得到的回归函数是：

(7)

由式(4)可知，如果确定了合适的惩罚参数C，不敏感损失函数ε和核函数形式就能确定SVR的具体形式。

2.2 PSO优化

粒子群算法是一种群体智能算法，最早由Kennedy和Eberhart于1995年提出，它的算法理念源于对鸟群捕食行为的研究。用数学语言表述：设粒子的搜索空间为D维，粒子的总数为N。其中，第i个粒子的当前位置是Xi=(xi1,xi2,…,xim)，它的当前速度为Vi=(vi1,vi2,…,vim)，这样当前时刻粒子i的最优位置是Pibest，整个群体的最优位置是Pgbest。然后每个粒子根据速度方程(8)和位置调方程(9)去更新其本身的速度和位置：

Vi(t+1)=ωVi(t)+c1rand1(Ptbest(t)-
Xi(t))+c2rand2(Pgbest(t)-Xi(t))

(8)

Xi(t+1)=Xi(t)+Vi(t+1)Xi(t)∈[-Xmax,Xmax]

(9)

其中，t为粒子的第t代；ω为惯性权值；c1,c2均为加速常数或称为学习因子，一般在(0,2]内取值；rand1和rand2为在(0,1]范围内变化的相独立的两个随机数。

支持向量回归机性能的衡量采用参数均方差MSE作为适应度函数，表示如下：

(10)

粒子群算法优化SVR参数的步骤如下：

步骤1：初始化种群和速度；

步骤2：计算粒子的适应度函数，并作为这个粒子的最优值，此时所在的位置也被看做是当下最优位置；

步骤3：速度更新和个体更新，根据式(8)，式(9)进行速度更新和个体更新；根据更新的位置再重新计算适应度函数，若新的适应度小就更新个体位置，否则就继承原来的位置；

步骤4：是否满足终止条件，判断是否返回到步骤2重新进行计算；

步骤5：输出结果为最优参数(c,g)，将其代入到SVR算法程序，构建模型。

3 气膜薄壳钢筋混凝土结构施工的成本预测

3.1 模型输入

影响项目成本的因素有：市场价格、企业的管理水平等。预测模型的输入参数应根据影响成本的因素来构建量化指标。本文采用了文献[3]的原始数据资料整理加工，形成气膜钢筋混凝土结构施工成本的量化指标如表1所示。将该数据样本分类，训练集为前9个，测试集为后3个，代入模型检验预测效果。

3.2 预处理数据

为提高预测的准确性，第一步应进行数据的预处理，它能减小量纲不同所带来的误差，对数据采取归一化预处理方式，公式为：

(11)

其中，xmax,xmin,xi分别为原始数据样本的最大值、最小值和实际值。

表1 施工成本预测数据

3.3 PSO-SVR成本模型的实现

PSO参数设置：算法终止代数T=200，种群数量popsize为20，学习因子c1=1.5,c2=1.7。采用PSO方法进行参数优化，得到的最优参数组合结果为：c=12.586 4，g=0.01。同时得到的适应度曲线如图2所示。原始数据与预测数据对比图如图3所示。从图中可以看出，样本的回归数据与预测数据结果的MSE都很小。达到了预测的精度要求。其中回归的数据误差由于是PSO的适应度函数的衡量标准，所以回归数据点的误差样本序号1～9要小于预测点10～12的误差。

4 结语

气膜薄壳钢筋混凝土结构作为一种新型结构，成本数据尚不完备，样本的容量也较小，成本预测困难，本文结合PSO算法的参数寻优特性和SVR算法的小样本数据非线性处理能力，构建预测模型，对气膜薄壳钢筋混凝土主体的成本进行了成功的预测。本文只对样本数据进行研究，精度达到了比较满意的结果；然而成本预测是对建设项目在实施之前对其成本的推断和预估，与建设过程中实际成本会有出入，从而产生不确定的预估误差。

参考文献:

[1] 严 静.基于改进灰色预测的成本预测模型构建[J].统计与决策,2014(3):39-41.

[2] 李万庆,陈明欣,孟文清,等.基于CSO-SVR的气膜钢筋混凝土储仓主体结构施工成本预测研究[J].数学的实践与认识,2017(1):105-111.

[3] 左 红.气膜钢筋混凝土主体结构施工成本预测研究[D].邯郸：河北工程大学,2017.

[4] 苗志同,曹 军.气膜钢筋混凝土结构穹顶储仓施工技术[J].山西建筑,2015，41(33):103-104.