锥面共形阵列非圆信号2D-DOA估计

张 羚, 郭 英, 邹 峰, 齐子森

(1. 空军工程大学信息与导航学院, 陕西 西安 710077; 2. 中国人民解放军驻西飞公司军事代表室,陕西 西安 710089; 3.中国人民解放军94826部队, 上海 200433)

0 引 言

“智巧蒙皮”的共形阵列天线在天线需求领域中有着广阔的市场,如航空航天、弹载雷达、声呐设备、移动通信等。近些年,就共形阵列天线的波束成形,测向以及优化布阵问题的研究已成为热点[1-6]。其中,极化参数与波达方向(direction of arrival, DOA)耦合,是共形阵列天线DOA估计与经典线阵、面阵DOA估计的主要区别与关键难点。

针对共形阵列的DOA估计问题,国内外学者已展开大量研究,相关成果主要集中在共形阵列快拍数据建模,盲极化DOA估计[1-3]以及信源方位与极化参数的联合估计[4-5]。其中,未利用非圆信号椭圆协方差非零特性的共形阵列天线的DOA盲极化算法[1-3]方面的研究已经相对成熟,算法通过对共形载体上阵元的优化布设并结合旋转不变子空间思想,划分可构成几何关系的几个距离矢量子阵对,在不需要或者获取不了极化参数参数的情况下得到角度参数的解析解。然而此类算法的空间谱估计能力的提升是以增加信噪比、获取更多采样数、增加阵元数为代价获得的,实际环境下较难实现。针对经典线阵、面阵,充分利用某些复随机信号如二进制相移键控(binary phase shift keying,BPSK)、幅移键控(amplitude shift keying,ASK)、振幅调制(amplitude modulation,AM)等调制信号的“非圆”性质来提高空间谱估计精度的研究已取得丰硕成果[7-12]。利用非圆信号[8]特性,将阵列虚拟扩展的思想从普通形式阵列引入到共形阵列,在同等条件下,比未利用非圆信号特性的算法估计效果要好,但该算法仅适用于柱面共形载体,存在着很大的局限性[6]。在实际应用中,如弹载导引头、机载首部等锥面结构,是更加常见的共形载体结构,然而已有算法并不适用于锥面共形阵列。所以,利用信号统计特性,提升共形阵列DOA估计效果的研究并不充分。

本文针对锥面共形阵列天线的DOA估计问题,利用非圆信号椭圆协方差矩阵不为零特性,对阵列进行虚拟扩展,并建立阵列天线的数据模型。通过全局以及局部坐标系的建立,合理的阵元布局,实现极化参数、阵元方向图与角度参数“去耦合”。在对独立信源进行二维角度估计过程中,创新性地将非圆-旋转不变子空间(non-circular estimation of signal parameters via rotation invariant technique, NC-ESPRIT)算法“移植”到具有多极化特性的共形阵列算法;在估计相干信源时,分别对真实阵元和虚拟阵元进行空间平滑预处理,扩展了算法的适用范围。最后通过计算机蒙特卡罗仿真实验验证锥面共形阵列非圆信号二维DOA(two dimensional-DOA,2D-DOA)算法的可行性和优越性。

1 锥面共形阵列数据模型

1.1 锥面共形阵列结构设计

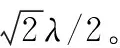
图1 阵列结构设计Fig.1 Design of array structure

上述阵列布局具有以下几个方面的优势:

(1) 由于信号的“非圆”虚拟扩展性,真实阵元和虚拟阵元是镜像对称的,所以按上述布局可使虚拟阵元与真实阵元置于一条母线上,可视为线阵,便于接收模型的建立。

(2) 由于窄带远场信号的假设前提,在同一母线上的阵元可以忽略其方向图指向的差异性。同一母线上布设的阵元响应同一来波信号的差别仅来自于相位差,从而可以构造适用于经典阵列天线非圆旋转不变技术估计信号参数算法的子阵对,简化了整体算法的复杂度。

(3) 在所构造的5个不同位置矢量的子阵对是利用NC-ESPRIT算法实现二维角度参数估计的关键,由于对导向矢量模型没有要求,因而有效克服共形载体的多极化特性。每对子阵对之间的距离矢量只包含信源的二维角参数,而对极化参数没有要求。因此基于上述阵元布局结构,应用NC-ESPRIT算法可实现对角参数信息和极化参数信息的去耦合,从而实现盲极化DOA估计。

(4) 在平面阵中[13]已经有利用子阵之间距离矢量的特殊性成功实现二维参数估计的案例,并给出了参数估计的解析解。尽管本文中子阵对之间的距离矢量并不是特殊值,但是可以利用锥面载体上设置的5条母线夹角之间的关系,结合l1,l2,l3子阵对的数据,可以获得二维角参数估计的解析解。再利用母线l4,l5子阵对的数据对多个来波信号进行参数配对。

1.2 锥面共形阵列非圆信号数据建模

由图1(c)可知:由于共形阵列天线的全局坐标系与局部坐标系并不一致,因此阵元方向图的指向也不同,所以需通过阵元方向图旋转[14]来完成共形虚拟扩展阵列DOA估计的第一步。m元共形阵列,n个窄带、最大非圆率点源以平面波入射(波长为),且在的情况下,以全局坐标系中的原点为参考点,共形阵列天线导向矢量:

(1)

u=sinθcosφX+sinθsinφY+cosθZ

(2)

|gi||pl|cosθigk=gi·pl=giθkθ+giφkφ

(3)

式中,u为信源单位矢量于全局坐标系的坐标表达形式;θ为来波俯仰角,表示来波位置矢量与全局坐标系中Z轴的夹角;φ为来波方位角,表示DOA矢量在XOY面上的投影与X轴的夹角;ri表示子阵中第i个阵元响应单位信号的表达式;gi为第i个阵元的方向图表示式;giθ,giφ分别为第i个阵元在信源构成的矢量基uθ,uφ上的单位矢量;kθ,kφ表示来波信号的极化状态;pl为来波信号的电场矢量;θigk为gi与pl之间的夹角;Pm是相对于坐标原点阵元位置矢量表达式。

将式(3)代入式(1)有

a(θi,φi)=aiθ(θi,φi)kiθ+aiφ(θi,φi)kiφ

(4)

当有n个入射信号时,可得流形矩阵为

A=[a(θ1,φ1),a(θ2,φ2),…,a(θn,φn)]=AθKθ+AφKφ

(5)

式中

Aθ=[aθ(θ1,φ1),aθ(θ2,φ2),…,aθ(θn,φn)]

Aφ=[aφ(θ1,φ1),aφ(θ2,φ2),…,aφ(θn,φn)]

Kφ=diag(k1φ,k2φ,…,knφ)

Kθ=diag(k1θ,k2θ,…,knθ)

叠加噪声后的非圆虚拟扩展快拍数矩阵可表示[8]为

(6)

由于最大非圆率信号具有关系[8,15]为

(7)

将式(7)代入式(6),得

AncS+Nnc=X0(nc)+Nnc

(8)

X=AS+N=(AθKθ+AφKφ)S+N

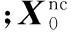
共形阵列天线阵元输出数据的协方差矩阵定义为

(9)

式中,(·)H表示取(·)的共轭转置;RS=E[SSH]为多个来波信号组成信源矢量的协方差矩阵;I2m为2m维单位矩阵;σ2为噪声功率。

然后,进行协方差矩阵Rnc特征值分解,即

(10)

式中,将特征值分解后得到的特征值按从小到大排序,取后n个值为主对角线元素的对角阵ΣS,并且将对应的特征矢量作为矩阵US的列向量;取前2m-n个值为主对角线元素的对角阵ΣN，并且将对应特征矢量作为矩阵UN的列向量；US代表的是协方差矩阵Rnc的信号子空间;UN则是噪声子空间。

取有限次快拍数,Rnc一致估计值为

(11)

2 非圆信号盲极化2D-DOA估计算法

本节分别针对独立信源、相干信源情况下,理论推导锥面共形阵列天线非圆信号盲极化2D-DOA估计算法的适用性。在阵列结构以及数据模型建立的基础上,利用各母线阵元非圆旋转不变性原理,建立同一母线上的阵列流形,由于各母线上阵元排布相同,因此可以将流形矩阵的理论推导过程推广到所设置的其他几条母线上。然后,利用非圆信号的虚拟扩展性对阵列接收模型进行阵元的虚拟加倍。最后根据解析解公式实现二维角度参数的分维估计。

2.1 基于NC-ESPRIT 锥面共形非圆信号算法

NC-ESPRIT算法[8]利用了旋转不变的信号子空间特性进行空间谱估计。该算法每构造一个结构完全相同且具有一定距离的子阵对可以估计一个参数。每条母线上的子阵对划分如图2所示。阵元1～m-1,m+1～2m-1和阵元2～m,m+2～2m构成一对子阵对,并且两阵列间隔0.5λ。尽管5条母线的距离矢量(阵元1与阵元2之间构成的距离矢量)的长度一致,但方向不同,理论上是可以估计5个参量,而本章只需要估计两个方位参数,但是由于3条母线之间的夹角不是特殊角,因此需要多增加一对子阵对,从而可以得到二维角参量的解析解。为应对多个来波信号,再增加两对子阵对用于参数配对。

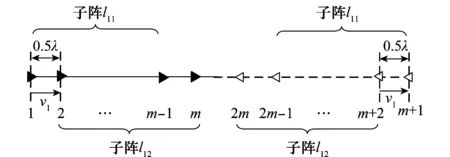
图2 子阵划分图Fig.2 Partition of subarray

子阵对1中的子阵1设为l11, 其接收数据为

X11=A11S+N11=(A11θKθ+A11φKφ)S+N11

(12)

子阵对1中的子阵2设为l12, 其接收数据为

X12=A12S+N12=(A11θKθ+A11φKφ)Φ1S+N12

(13)

Φ1=diag[exp(-jw11),exp(-jw12),…,exp(-jw1n)]

(14)

w1i=(2π/λ)dv1·ui=πv1·ui=

π[sinθv1cosφv1sinθicosφi+

sinθv1sinφv1sinθisinφi+cosθv1cosθi]

(15)

母线l1上,真实阵元的快拍数据为

X1=A1S+N1=(A1θKθ+A1φKφ)S+N1=

[X11;X12(m-1,∶)]

(16)

特别地,NC-ESPRIT利用了非圆信号的特征,虚拟扩展阵列的同时,接收数据维数也相应加倍,即

(17)

将式(8)代入式(17),可得

(18)

由式(10)和式(11)可得子阵对1输出数据的协方差矩阵为

(19)

子阵对1的流形矩阵张成的子空间与特征值分解处理后得到的信号子空间是相同的,即

span{A1(nc)}=span{US1}

(20)

因此,有且只有一个非奇异矩阵T1,使得

A1(nc)=US1T1

(21)

由于A1(nc)的ESPRIT特性,因此有

J1(nc)A1(nc)Φ1=J2(nc)A1(nc)

(22)

式中,选择矩阵[16]J1(nc),J2(nc)为

式中,I(m-1)(m-1)是一个(m-1)×(m-1)维单位阵,0(m-1)(m-1)是一个(m-1)×(m-1)维的零矩阵,0(m-1)1是一个(m-1)×1维的零向量。

根据式(21)的ESPRIT关系,式(22)以信号子空间作为表达方式为

(23)

(24)

(25)

exp(-jwli)=tli

(26)

结合关系α1=π-α3,α2∈(α1,α3)解式(27)～ 式(29)有

φi=

(27)

(28)

zji=angle(tli)/(2πd)，j=1,2,3

(29)

式中,θi,φi分别表示第i个来波信号在全局坐标系下的俯仰和方位角;θv b,φv b(b=1,2,3;i=1,2,…,n)分别表示子阵对b的距离矢量在全局坐标系中的俯仰角和方位角;angle(·)表示求复数(·)的相位角。

exp(-jw5i)=exp(-jw1i)exp(-jw2i)

(30)

exp(-jw4i)=exp(-jw1i)exp(-jw3i)

(31)

借鉴式(15)可知

wli=(2π/λ)ΔPl·ui=

(2π/λ)|ΔPl|(sinθΔPlcosφΔPlsinθicosφi+

sinθΔPlsinφΔPlsinθisinφi+cosθΔPlcosθi)

(32)

min{|t5i-t1jt2k|,i,k=1,2,…,n}

(33)

t1j与满足式(34)的t3k相对应,即

min{|t4i-t1jt3k|,i,k=1,2,…,n}

(34)

综上可以完成满足当入射信号为独立信源时,锥面共形虚拟扩展阵列算法的理论推导,将算法步骤总结如下:

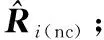
步骤4根据式(33), 式(34)实现参数的配对;

步骤5结合式(26)～式(29),求得最终的二维角参数φi,θi。

2.2 锥面共形阵列非圆信号解相干预处理

当入射信号为相干信源时,信号协方差矩阵(式(9)中的RS)的秩受到损耗,不再等于信源个数,且信号子空间维数降低,不再等于阵列流形矩阵的秩。因此通过特征值分解得到信号子空间与流行矩阵所张成的信号子空间不一致,这导致了特征值分解类DOA算法无法适用于相干信源情况。

就上述情况,拟采用空间平滑算法对入射的相干信号进行解相干,具体思路如下:

空间平滑算法主要运用于均匀线阵,是因为利用了均匀线阵的平移不变性。方法是将均匀线阵划分成相互重叠且结构完全相同的L个子阵,因此每个子阵阵元数相同(这里设为q个)且每个子阵包含的方位信息也是一致的,将各子阵的自协方差矩阵进行算数平均得到q阶子阵列协方差矩阵。当子阵中所包含的阵元个数大于所需探测的信源个数时,经空间平滑算法处理得到协方差矩阵分解后得到的信源协方差矩阵恢复为满秩。锥面共形虚拟扩展阵列由于同时受到共形载体曲率以及建立虚拟扩展阵列数据矩阵特殊性的影响,在“移植”空间平滑算法时存在一定难度。本节通过合理的阵元布局,将同一母线上真实阵元部分以及虚拟阵元部分分别进行子阵划分,又由于同一母线上的阵元对同一来波信号而言阵元方向图响应是近似一致的,可以克服由共形载体曲率所带来的影响,此时空间平滑算法将得以适用。

同一条母线上真实阵元构成的子阵接收数据矩阵为

XlR=AlRS+NlR

(35)

AlR=[alR(θ1,φ1),alR(θ2,φ2),…,alR(θn,φn)]

(36)

(37)

同样,同一条母线上虚拟阵元构成的子阵接收数据矩阵为

XlI=AlIS+NlI

(38)

AlI=[alI(θ1,φ1),alI(θ2,φ2),…,alI(θn,φn)]

(39)

(40)

由于圆锥面上同一条母线的曲率不发生变化,因此同一母线上阵元方向图指向一致,所以

rl1=rl2=…=rlm=rlR

(41)

rlm+1=rlm+2=…=rl2m=rlI

(42)

结合式(37)与式( 41),得到

(43)

所以有

AlR=rlR[alR0(θ1,φ1),alR0(θ2,φ2),…,alR0(θn,φn)]=rlRAlR0

(44)

同理,结合式(40)与式(42),得到

AlI=rlI[alI0(θ1,φ1),alI0(θ2,φ2),…,alI0(θn,φn)]=rlIAlI0

(45)

式中,AlR0和AlI0可视为均匀线阵的流形矩阵。将同一母线上的真实阵元和对应母线上的虚拟阵元构成的阵列分别平滑处理为L个子阵,每个子阵的阵元数为q,第i个真实子阵和虚拟子阵接收数据的协方差矩阵分别是

(46)

(47)

(48)

(49)

(50)

将式(44)和式(46)代入式(49),得

(51)

所以有

(52)

同理将式(45)和式(47)代入式(50)后有

(53)

(54)

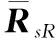
本节完成了锥面共形阵列天线非圆信号的空间平滑解相干算法的理论推导,将算法步骤总结如下:

步骤1求同一条母线上真实阵元构成的子阵接收数据矩阵Xlr和虚拟阵元构成的子阵接收数据矩阵XlI；

步骤2根据同一母线圆锥面载体曲率不变的特点,获得简化后得流形矩阵矩阵AlR0和AlI0;

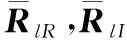
步骤5后续步骤同独立信源时步骤3～步骤 5。

3 仿真验证

本节就所提算法的有效性,精确度等性能指标进行蒙特卡罗仿真实验,并和相同真实阵元布局的非扩展锥面阵列天线DOA估计算法进行对比,验证相关结论。这里进行对比的算法是基于图1(a)中真实阵元部分,即无虚拟扩展步骤的算法 (第2.1节算法的对比算法是文献[1],除了将文献[1]中的母线数目设置为5条,其他仿真条件皆与所提算法一致,前3条用于参数估计,额外2条母线用于参数配对;第2.2节算法对比算法是文献[2]),图3～图8中无NC标注是对比算法,标注NC的为本文所提算法。

在本文蒙特卡罗仿真实验中,将估计值与真值的偏差小于2°的情况认定为估计成功。将主要性能指标列举如下:

估计偏差=abs(估计均值-真值)

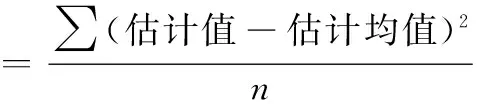
式中,n为成功估计的实验次数。

3.1 仿真实验1

(1)仿真条件

仿真结果如图3～图5所示。

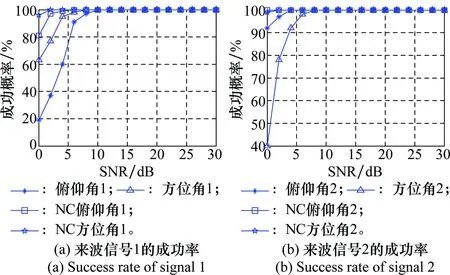
图3 独立信源成功率分析Fig.3 Success rate analysis of independent signals

图4 独立信源估计偏差分析Fig.4 Estimation deviation analysis of independent signals

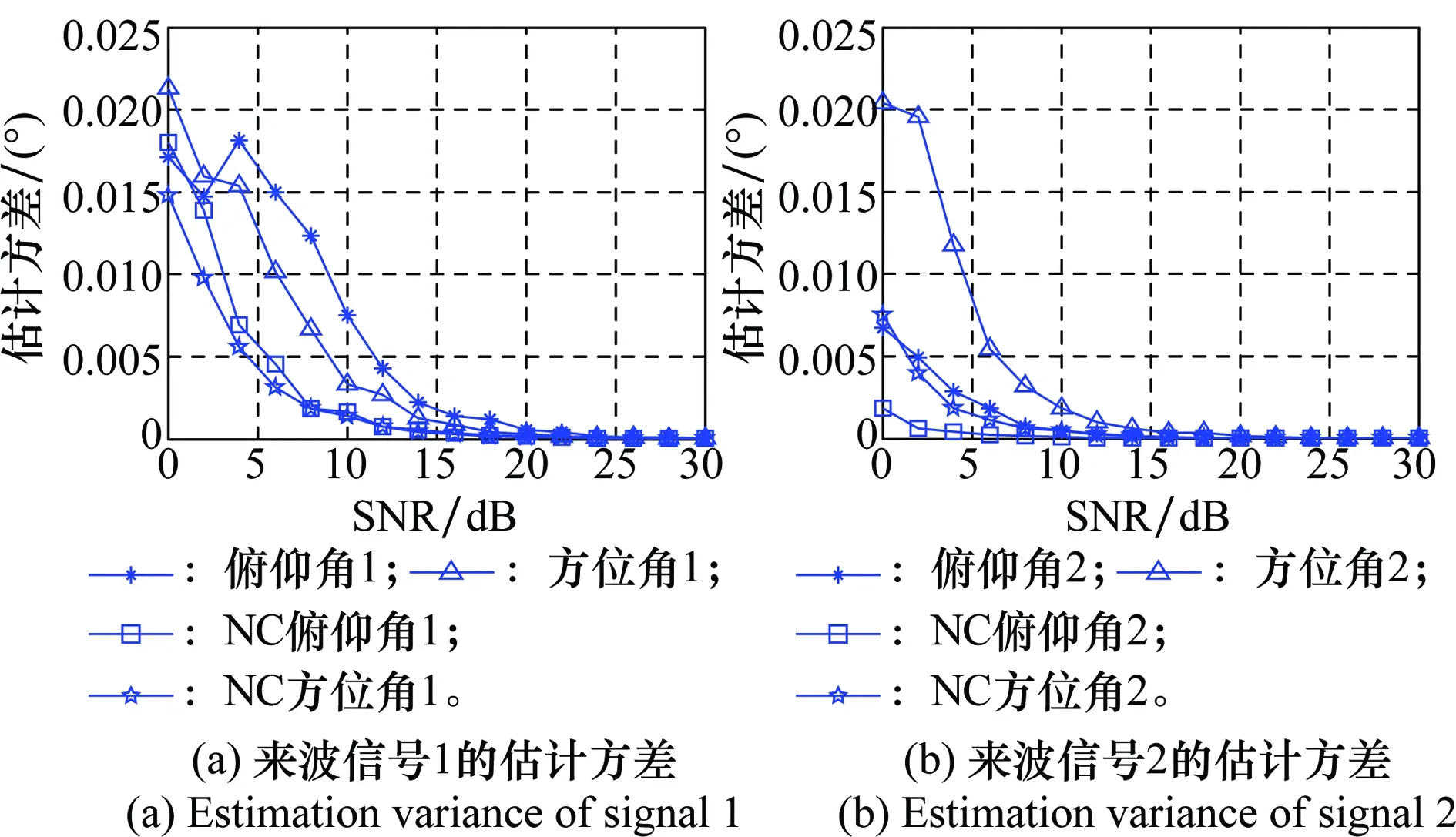
图5 独立信源估计方差分析Fig.5 Estimation variance analysis of independent signals

(2) 结果分析

当来波信号是独立信源时,第2.1节所提算法中在SNR较低(0～10 dB)的情况下,成功率随SNR成正比,并趋于100%,在SNR较低(0～15 dB)的情况下,参数的估计方差随SNR呈反比的趋势,俯仰角的方差从整体上看要小于方位角。在与文献[1]算法比较中:SNR<10 dB时,所提算法探测来波信号俯仰角和方位角的成功率皆高于文献[1]算法;所提算法估计偏差的波动幅度要小于文献[1]算法;非虚拟扩展阵列天线(文献[1])的二维角参数估计方差大于虚拟扩展阵列天线(本文所提算法)。

3.2 仿真实验2

(1)仿真条件

来波信号是相干信源,其余条件同实验1。

仿真结果如图6～图8所示。

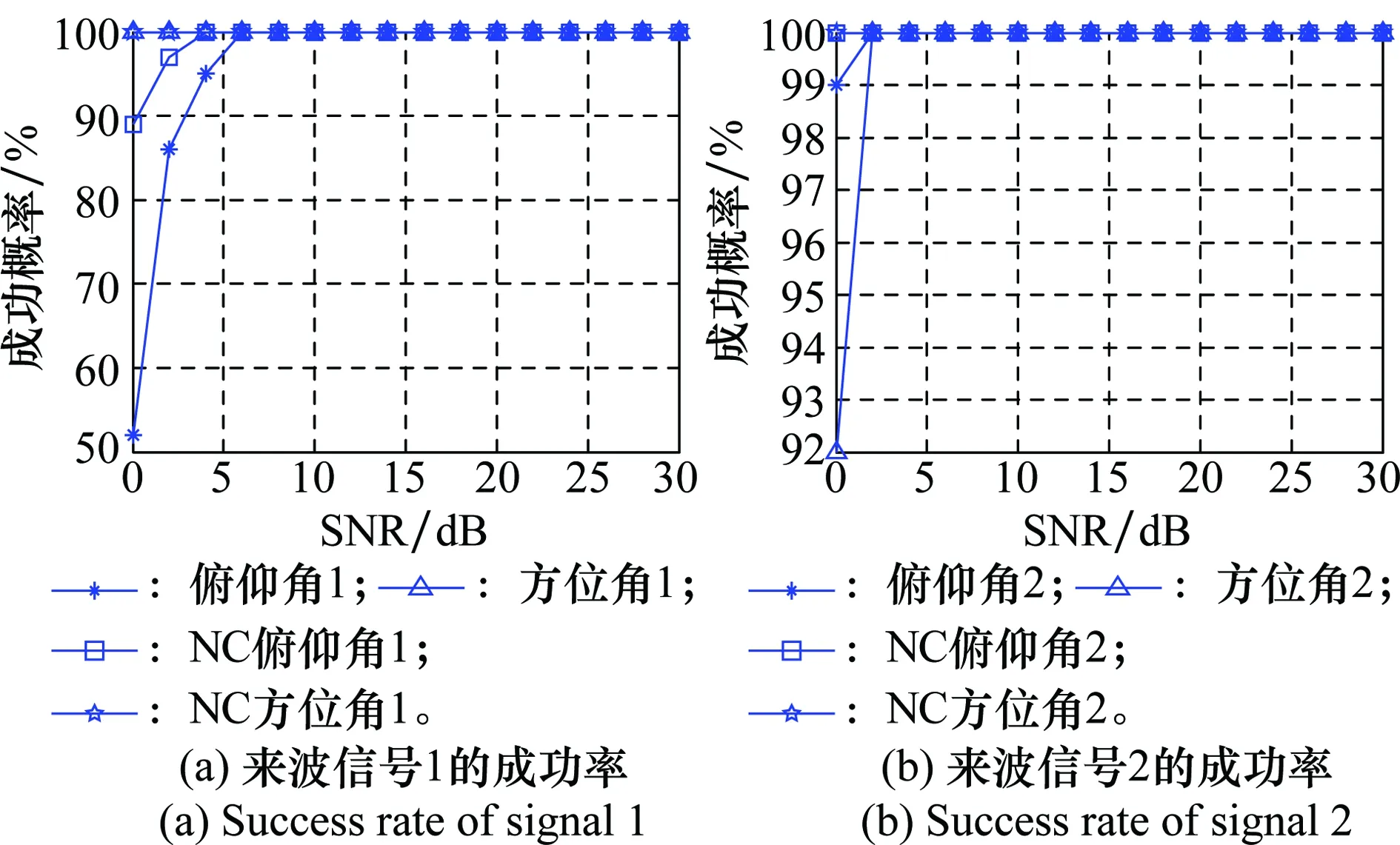
图6 相干信源成功率分析Fig.6 Success rate analysis of coherent signals

图7 相干信源估计偏差分析Fig.7 Estimation deviation analysis of coherent signals

图8 相干信源估计方差分析Fig.8 Estimation variance analysis of coherent signals

(2) 结果分析

当来波信号是相干信源时,第2.2节所提算法探测信源方位、俯仰角的成功概率与信噪比呈正比,并且趋向于100%,在SNR较低(0～5 dB)的情况下,二维角参数的估计方差随SNR成反比。其次,在SNR<10 dB时,第2.2节所提算法对相干信号俯仰角和方位角的探测成功率要高于文献[2]算法的成功率。第2.2节算法的估计偏差的波动幅度要小于文献[2]中的波动幅度。非扩展阵列天线对相干信源的二维角参数估计方差要明显大于虚拟扩展阵列天线。

4 结束语

锥面共形载体合理的阵元布局,以及利用非圆信号虚拟扩展性,成功建立对应的数据模型,算法基于NC-ESPRIT思想,在无需任何极化参数和阵元方向图[18-20]参数信息的情况下,利用母线阵元具有不同距离矢量的性质,得出俯仰角和方位角的解析解,实现角度参数的分维估计。针对相干信源而言,增加空间平滑算法步骤,实现了锥面共形虚拟扩展阵列情况下的角度参数盲估计,扩展了本文所提算法的使用范围。同时,所提算法估计性能在较低SNR的情况下,较之非扩展阵列有很大的提升,算法实现简单,硬件开销小。

参考文献：

[1] 齐子森, 郭英, 姬伟峰, 等. 锥面共形阵列天线盲极化DOA估计算法[J]. 电子学报, 2011,33(8):1727-1731.

QI Z S, GUO Y, JI W F, et al. Blind DOA estimation algorithm for conical array antenna with respect to polarization diversity[J]. Acta Electronica Sinica, 2011, 33(8): 1727-1731.

[2] 齐子森,郭英,王布宏,等.锥面共形阵列天线相干信源盲极化DOA估计算法[J].系统工程与电子技术,2011,33(6):1226-1230.

QI Z S, GUO Y, WANG B H, et al. Blind DOA estimation algorithm of coherent sources for conical conformal array antenna with respect to polarization diversity[J]. Systems Engineering and Electronics, 2011, 33(6): 1226-1230.

[3] 齐子森, 郭英, 王布宏, 等. 柱面共形阵列天线盲极化波达方向估计算法[J]. 电波科学学报, 2011, 26(2): 245-252.

QI Z S, GUO Y, WANG B H, et al. Blind polarization diversity DOA estimation on cylindrical conformal array antenna[J]. Chinese Journal of Radio Science, 2011,26(2):245-252.

[4] 张树银,郭英,齐子森,等.基于子空间原理的共形阵列多参数联合估计算法[J].系统工程与电子技术,2012,34(6):1146-1152.

ZHANG S Y, GUO Y, QI Z S, et al. Subspace-based multiple parameter estimation algorithm for incident signals with conformal array[J].Systems Engineering and Electronics,2012,34(6):1146-1152.

[5] 齐子森, 郭英, 王布宏, 等. 共形阵列天线信源方位与极化状态的联合估计算法[J]. 电子学报, 2012, 40(12): 2562-2566.

QI Z S, GUO Y，WANG B H,et al.Joint DOA and polarization estimation algorithm for conformal array antenna[J]. Acta Electronica Sinica, 2012, 40(12): 2562-2566.

[6] 匡开锋,徐友根,刘志文.共形阵列非圆信号波达方向估计算法[J].信号处理,2015,31(5): 551-558.

KUANG K F, XU Y G, LIU Z W. Direction of arrival estimation for noncircular signals using conformal array[J]. Journal of Signal Processing, 2015,31(5): 551-558.

[7] GALY J. Antenne adaptative: du second ordre aux orders superieurs. Applications aux signaux de telecommunications[D]. Toulouse, 1998.

[8] STEINWANDT J, ROEMER F, HAARDT M. Performance analysis of ESPRIT-TYPE algorithms for non-circular source[C]∥Proc.of the IEEE International Conference on Acoustics, Speech and Signal Processing, 2013: 3986-3990.

[9] ZOUBIR A, CHARGE P, WANG Y. Noncircular sources localization with ESPRIT[C]∥Proc.of the European Conference on Wireless Technology, 2003.

[10] 孙心宇, 周建江. 非圆传播算子DOA估计算法[J]. 数据采集与处理, 2013, 28(3): 313-318.

SUN X Y, ZHOU J J. PM method for noncircular signals[J].Journal of Data Acquisition and Processing, 2013, 28(3): 313-318.

[11] 司伟建,林晴晴,张铁军.基于矩阵重构的非圆信号ESPRIT算法[J].中南大学学报(自然科学版),2013,44(12):4936-4941.

SI W J, LIN Q Q, ZHANG T J. ESPRIT algorithm for non-circular signals based on matrix reconstruction[J]. Journal of Central South University(Science and Technology),2013,44(12): 4936-4941.

[12] 刁鸣,丁兆明,高洪元,等.基于特征空间算法的非圆相干信源DOA估计[J].哈尔滨工程大学学报,2014,35(12):1559-1563.

DIAO M, DING Z M, GAO H Y, et al. Estimating direction of arrival of non-circular coherent signals based on ES-DOA estimation algorithm[J]. Journal of Harbin Engineering University, 2014, 35(12): 1559-1563.

[13] LI J, COMPTON R T J. Two-dimensional angle and polarization estimation using the ESPRIT algorithm[J]. IEEE Antennas and Propagation Magazine, 1992, 40(5): 550-555.

[14] WANG B H, GUO Y. Array manifold modeling for arbitrary 3D conformal array antenna[C]∥Proc.of the IEEE International Workshop on Antenna Technology, 2008:562-565.

[15] 刘剑. 非圆信号波达方向估计算法研究[D]. 长沙:国防科技大学,2007.

LIU J. DOA estimation algorithms for noncircular signals using sensor arrays[D]. Changsha: National University of Defense Technology, 2007.

[16] 郑春弟. 基于非圆信号的空间谱估计算法研究[D]. 西安:西安电子科技大学,2006.

ZHENG C D. A study of spatial spectrum estimation techniques for non-circular sources[D]. Xi’an: Xidian University, 2006.

[17] SHAN T J, WAX M, KAILATH T. On spatial smoothing for estimation of coherent signals[J]. IEEE Trans.on Acoustics Speech & Signal Processing, 1985, 33(4): 806-811.

[20] WOHLER M, HARTMANN M, NOWAK T. Impact of antenna pattern modeling errors on RSSI-based DOA estimation[C]∥Proc.of the International Workshop on Antenna Technology:Small Antennas,Innovative Structures, and Applications,2017:167-170.