非严格优先权下许可相位左转车辆侵占时距分布模型
曲昭伟,白乔文,陈永恒,熊 帅,邓晓磊
(吉林大学交通学院,长春130022)
0 引言
目前,针对于许可相位下交通流微观行为特性的研究多是建立在严格优先权的前提下进行的,现有的Vissim等仿真软件对于这类左转车流的处理也都是使其遵循明确的让行规则沿着固定的路径通过交叉口.然而,在中国、挪威、芬兰等国家,驾驶员并不是严格按照让行规则行驶的[1],左转车辆与直行车辆在许可相位下争夺优先权的现象经常发生.这种抢行行为与传统间隙理论下遵循严格优先权的车辆行为有着本质上的区别,现有的交通流微观特性研究已经不能够解释这类现象.因此,研究非严格优先权下许可相位左转交通流的微观行为特性有助于深入理解抢行车流的运行机理,建立更符合实际的微观仿真模型,进而为交叉口服务水平和安全性评价奠定基础.
在这种非严格优先权下讨论左转车辆的穿越行为,传统的间隙理论已不再适用,也有学者提出了一些方法来分析车流的延误、通行能力和行为决策.Troutbeck[2]、马东方[3]等考虑到高饱和度条件下,穿越车流会对主路车流的优先权造成一定的影响,从而在间隙理论的基础之上建立了有限优先条件下的穿越车流通行能力;王炜[4]和孟永平[5]则不再使用间隙理论,而是将互相穿越的车流分配了相等的通行权,采用车队分析法假定两股冲突车流以车队的形式交替通过交叉口,分析主次车流穿越的通行能力和延误时间;Liu[6]则通过采集到的1 070组车辆穿越数据,采用分类回归树的方法确定了穿越车流的抢行/让行的行为决策及相关影响因素;Bai等[7]根据大量数据的调查,发现左转车辆在许可相位中会以“左转车辆组”的形式运行,一旦前面的左转车辆获得了一个可穿越间隙,后续的跟随穿越车辆会尽可能的保持一个较小的间隔连续通过交叉口,导致直行车流产生了较大的延误.
在非严格优先权下,左转车辆在时间上对于直行车流的侵占效应能够直观地体现出抢行车流的微观行为特性.因此,本文在前人研究的基础之上,以许可相位下的左转车辆组为研究对象,以侵占时距为出发点,考虑到左转车辆通过时,交叉口内对向直行车辆不同的存在状态,利用多种分布模型对不同状态下的侵占时距分布进行拟合,并通过Kolmogorov-Smirnov检验对各种模型的拟合优度进行定量分析,研究了左转车辆抢行现象的微观交通流特性.侵占时间分布模型的建立能够为非严格优先权下许可相位左转交通流微观特性的进一步研究提供一定的理论依据和参考.
1 数据采集
1.1 侵占时距
由于左转车辆只要越过了直行车道边缘线在交叉口内的延长线,就会侵犯到直行车辆的通行权,因此研究中将侵占时距定义为前后两辆左转车的左前轮通过对向直行车道左侧车道边缘线在交叉口内延长线的时间差,如图1所示.侵占时距与车头时距的概念有所不同.车头时距是前后两辆车经过道路上同一地点的时间差[8],但对于许可相位下的左转车辆来说,它们并非都沿着同样的轨迹行驶,也就并不存在这样的一个点,只能以对向直行车道左侧车道边缘线在交叉口内延长线为断面,来研究相邻两辆左转车通过这个断面的时距分布.

图1 侵占时距示意图Fig.1 Definition of the encroaching time interval
1.2 左转车辆组
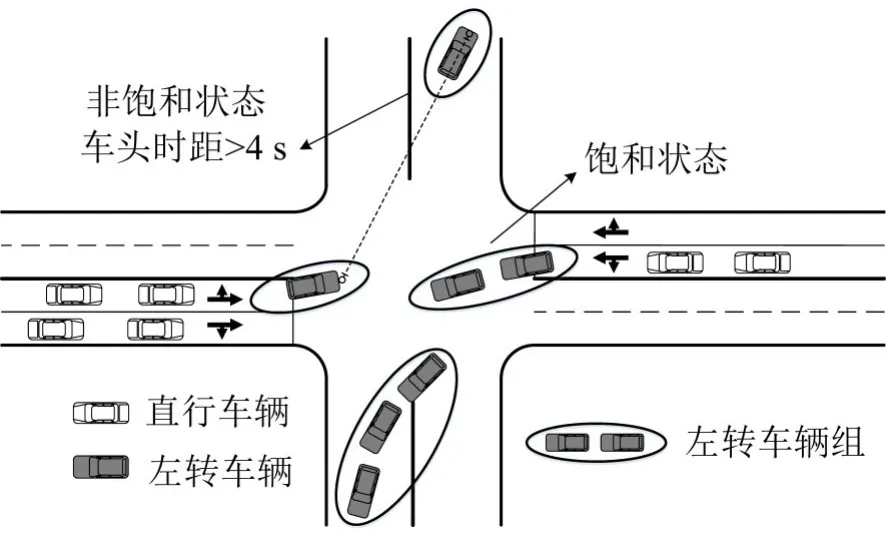
图2 左转车辆组的定义Fig.2 Definition of a left-turn group
此外,研究中根据左转车辆通过时,交叉口内对向直行车辆不同的存在状态,分成以下4种交通状态:绿灯初期,左转车辆抢行先于直行车通过交叉口(状态1);左转车辆进入交叉口时,没有对向直行车流(状态2);左转车辆进入交叉口时,对向进口道外侧车道有直行车流(状态3);左转车辆进入交叉口时,对向进口道内侧车道有直行车流(状态4),如图3所示,并分别采集了每种状态下侵占时距数据.
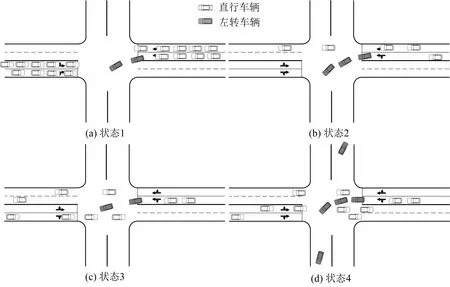
图3 交叉口内对向直行车辆4种存在状态Fig.3 Four states of through flows at an intersection with a permissive phase
1.3 数据采集过程
选取长春市皓月大路—和平大街交叉口作为研究交叉口,解放大路—同志街交叉口作为对比交叉口,飞跃路—东风大街、自由大路—同志街交叉口作为验证交叉口,4个交叉口的基本信息如表1所示.结合图4可以看出,带有左转许可相位的皓月大路—和平大街交叉口与带有左转保护相位的解放大路—同志街交叉口几何条件十分相似,非常适合进行对比分析.
在调查地点周边高点进行俯拍视频采集,以车辆左前轮触地点为基准,使用Track Pro软件对左转车流的侵占时距及通过停止线断面的车头时距进行人工提取,精度可达0.1 s.调查在6个工作日14:00-16:00进行,总计获取3 230个样本数据.
2 分布差异性分析
首先,对许可相位和保护相位2种控制方式下的侵占时距和停止线断面的车头时距进行描述性统计分析,得到表2和图5中的箱线图.可以看出:
(1)2种控制方式下,侵占时距都属于正偏态的尖峰分布,正态性较差,显示出侵占时距都集中在均值左侧,驾驶员倾向于选择一个较小的侵占时距通过断面.

图4 交叉口调查断面示意图Fig.4 The cross-section of the two studied sites
(2)许可相位下侵占时距较车头时距均值的下降幅度明显大于保护相位,说明许可相位下的左转车辆会在短时间内快速地侵占对向直行车 道,抢行行为十分严重.
在治疗期间所有患者禁止食用难以消化、油腻性、刺激性的食物,对照组患者采用常规药物治疗,即口服吗丁啉,10mg/次,一天三次[2]。研究组患者加强针刺穴位治疗,其具体如下:取双侧四缝穴,位置在第二到第五指掌面,第一、二节横纹中央。用五号、六号注射针头,左手扶住手指,刺手快速点刺。点刺深浅根据年龄、体质决定,刺后用双手挤出少许血液或淋巴液即可。取坐位,双手伸开,常规消毒,将五号、六号注射针头,垂直、快速的刺入穴位,快速起针,不用留针。

表1 调查地点基本信息Table1 Basic information of studied sites
(3)许可相位下的侵占时距呈现尖峰厚尾分布,一方面说明侵占时距会高度集中于均值附近,大多数的车辆行为是相似的;但另一方面也会说明离群数据的极端性较大,表明了左转车辆行为的复杂性.

表2 2种控制方式下车头时距与侵占时距的统计性描述Table 2 Statistic description of the encroaching time interval and time headway
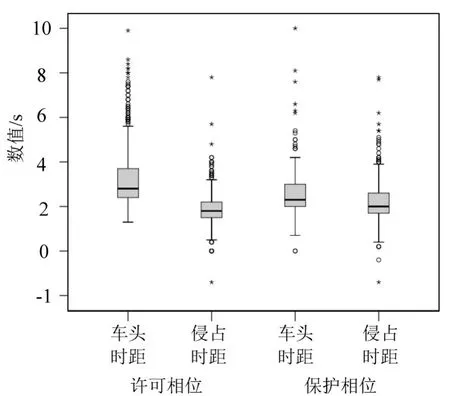
图5 许可相位与保护相位下车头时距和侵占时距的箱线图Fig.5 Boxplots of time headways and encroaching intervals with permissive/protect phase
为了能够准确地说明分布上的差异性,对各类样本数据进行非参数检验.在对2种控制方式下的侵占时距分布进行Mann-Whitney检验后,检验结果也证明了不同控制方式下的侵占时距分布存在显著性差异.而通过Wilcoxon符号秩检验对许可相位下侵占时距与车头时距进行配对样本的非参数检验结果,则显示出侵占时距分布与车头时距分布是存在显著性差异的,不能直接通过车头时距分布来描述侵占时距分布.2种非参数检验结果如表3所示.

表3 样本数据的非参数检验结果Table 3 Results of nonparametric tests
3 分布模型与参数估计
考虑到侵占时距与车头时距定义上的相似性,可以结合侵占时距的描述性统计结果,参考相关车头时距分布模型来建立侵占时距的分布模型.国内外学者在研究中经常使用移位负指数模型、Erlang模型、Weibull模型及Lognormal模型来拟合车头时距的分布.除此之外,Jang还应用了具有2个形状参数、灵活性更强的Johnson SB模型来拟合车速较低时的干线车头时距,其基本模型如式(1)所示[9].

式中:y=(x-ξ)/λ;ξ为位置参数;λ为尺度参数,λ>0;γ和δ为形状参数,δ>0.
曲昭伟等尝试运用与Lognormal分布形状相似的Log-Logistic模型对高密度、低速度下环岛的车头时距进行拟合,获得了更好的拟合效果,其基本形式如式(2)所示[10].

式中:α为形状参数,α>0;β为尺度参数,β>0.
此外,考虑到Erlang分布和负指数分布是Gamma分布模型下的特殊状态,将Gamma分布模型也纳入到拟合优度检验中.
利用最大似然估计法求解这7种分布模型概率密度函数的参数,并采用Kolmogorov-Smirnov检验对各种分布模型的拟合优度进行定量评价.

表4 7种分布模型拟合优度检验Table 4 Goodness of fit test for seven distribution models
结合图6、图7和表4中的数据,移位负指数分布的拟合效果较差,仅在状态2中通过了K-S检验,Log-Logistic分布的拟合效果最好,不论是分别对4种状态进行拟合,还是对总体数据进行拟合,都通过了检验.
在状态1下,仅单调递减的移位负指数模型没有通过检验.这一结果说明,虽然左转车辆会发生抢行行为并趋向以较小的侵占时距通过交叉口,但是受到驾驶员反应时间等因素的影响,车辆在绿灯启亮初期达不到稳定的饱和释放状态,因此并不会出现侵占时距越小发生概率越大的现象.
与之不同的是,在状态2中,移位负指数分布通过了K-S检验,这一结果从侧面说明了在非绿灯初期通过的左转车队车辆在交叉口内没有对向直行车流时,侵占时距越小左转车辆会发生抢行行为的概率越大.其位置参数值γ=1.2,表明会有更多的驾驶员期望以1.2 s的侵占时距通过交叉口.而该状态下,通过停止线断面的车头时距最小值为1.8 s,说明跟随车辆会提前转向,选择比前车略短的路径以便尽早地侵占对向直行车道.
对于后2种状态来说,Log-Logistic分布、Gamma分布和Erlang分布都通过了K-S检验,而由于调查数据不符合Johnson SB模型分布特征,该模型已完全失效.Gamma分布和Erlang分布在侵占时距较小时拟合值明显偏大,在侵占时距较大时拟合值明显偏小,拟合稳定性欠佳.Lognormal模型在前2种状态下的拟合优势仅保持到了状态3,在状态4下已不再适用.Log-Logistic模型在这2种状态都取得了最好的拟合程度,而其在状态4下的K-S检验值为0.057,更是明显小于其他分布模型,拟合优势显著.
根据以上分析结果可以得到,Log-Logistic模型非常适用于描述侵占时距的分布.该模型在4种状态及总体下的参数估计值及函数图像如表5和图8所示.参数α>1说明5个模型均为单峰分布,而α值越大,离散程度越小,4种状态下α的值依次递减,说明交叉口内有对向直行车辆时,会使得侵占时距分布离散程度略有增加.参数β代表了分布模型的中值,4种状态下β值呈现依次递减,而总体数据下分布模型中值介于状态3和状态4的中值之间,表明左转车辆通过时,交叉口内有对向直行车辆的状态是极其多发的,对侵占时距总体分布的影响较大.
4 适用性验证
为了验证Log-Logistic侵占时距分布模型的适用性,利用飞跃路—东风大街和自由大路—同志街交叉口调查数据进行分析验证,分析结果如表6所示.Log-Logistic模型在2个交叉口所有的状态下都通过了检验,且超过半数的状态下拟合优度位居7种分布模型之首.从模型参数上来看,后2种状态下表征离散程度的α值都大于了前2种状态,而表征中值的β则根据交叉口内对向直行车流不同的存在状态仍然呈现了依次递减的趋势,这与皓月大路—和平大街交叉口数据的拟合结果是一致的.通过适用性验证,说明了Log-Logistic模型对于描述非严格优先权下许可相位左转车辆的侵占时距分布是有效的.

图6 4种状态下侵占时距概率密度函数分析图Fig.6 Probability distribution of encroaching interval at four different states

图7 样本总体侵占时距概率密度函数分析图Fig.7 Probability distributions of encroaching intervals forall samples
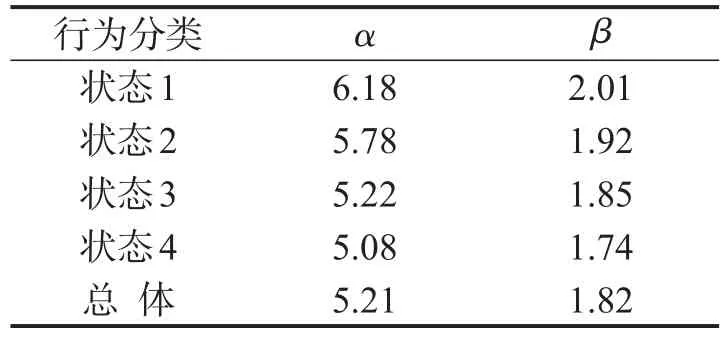
表5 Log-Logistic分布模型参数估计值Table 5 Estimated parameter values of Log-Logistic model
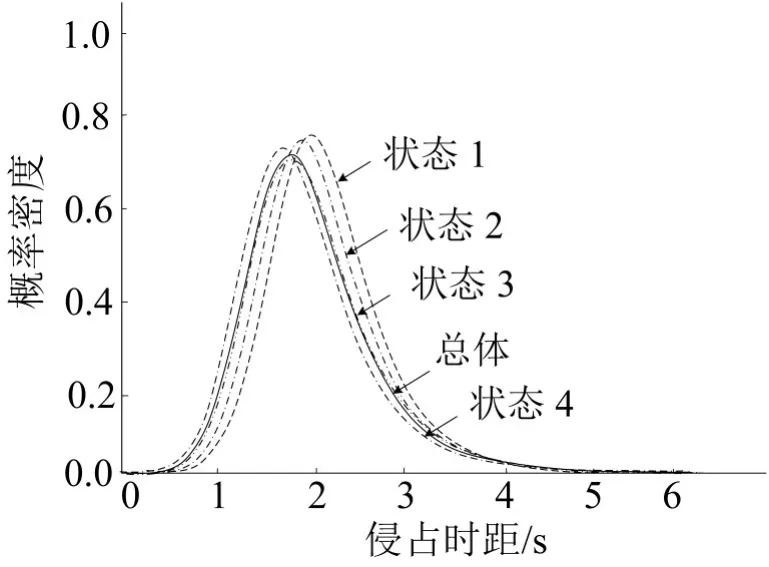
图8 不同状态的Log-Logistic分布模型的函数图像Fig.8 Graphs of Log-Logistic distributions under different states
5 结论
通过对4个交叉口大量左转车辆侵占时距的调查,结合Mann-Whitney检验、Wilcoxon符号秩检验、Kolmogorov-Smirnov检验及最大似然估计等方法,对非严格优先权下许可相位左转车辆侵占时距进行了分析与建模,得到了以下几个主要结论:

表6 2个验证交叉口的拟合优度分析Table 6 Results of the verification test at other two intersections
(1)在非严格优先权下,左转车辆的驾驶员会倾向于选择一个较小的侵占时距通过交叉口;
(2)许可相位下左转车流侵占时距较车头时距均值的下降幅度明显大于保护相位,左转车辆抢行行为十分严重;
(3)Log-Logistic模型对于非严格优先权许可相位左转车流侵占时距分布的拟合效果最优;
(4)在交叉口内有对向直行车辆时,侵占时距的Log-Logistic分布模型参数α和β的值要小于交叉口内没有对向直行车辆的状态.
本文所建立的侵占时距分布模型能够为非严格优先权下许可相位左转交通流微观特性奠定理论基础,进而可以将模型扩展应用到交通仿真中,为非严格优先权下交叉口通行能力分析、交通状态评价研究提供一定的参考.在后续研究中,还将通过扩大调查交叉口数量和侵占时距样本数量,具体研究Log-Logistic分布模型中影响α和β参数值变化的因素,以期增强侵占时距分布模型的普适性.
参考文献:
[1]LIN D,MA W,LI L,et al.A driving force model for non-strict priority crossing behaviors of light-turn drivers[J].Transportation Research Part B Methodological,2016,83(2016):230-244.
[2]TROUTBECK R J,KAKO S.Limited priority merge at unsignalized intersections[J].Transportation Research Part A:Policy&Practice,1999,33(1999):291-304.
[3]马东方,王殿海,杨希锐,等.有限优先下交叉口信号设置的临界流量依据[J].东南大学学报(自然科学版),2010,40(4):860-865.[MA D F,WANG D H,YANG X R,et al.Critical traffic volume of traffic signal warrant under limited priority condition[J].Journal of Southeast University(Natural Science Edition),2010,40(4):860-865.]
[4]王炜.无控制交叉口通行能力及延误的车队分析法[J].重庆交通大学学报(自然科学版),1989,6(3):36-44.[WANG W.Platoon method of analyzing capacity and delay of non-signalized intersection[J].JournalofChongqing JiaotongUniversity (Natural Science Edition),1989,6(3):36-44.
[5]孟永平,邓卫,葛亮.基于车队法的双车道无控制交叉口通行能力分析[J].公路交通科技,2005,22(12):119-122.[MENG Y P,DENG W,GE L.Analysis for two-roadways uncontrolled intersection of capacity by motorcade analysis method[J].Journal of Highway&Transportation Research&Development,2005,22(12):119-122.]
[6]LIU M,LU G,WANG Y,et al.Analyzing drivers’crossing decisions at unsignalized intersections in China[J].Transportation Research PartF Traffic Psychology&Behaviour,2014,24(2014):244-255.
[7]BAI Q W,CHEN Y H,QU Z W,et al.Nonstrict priority left-turning maneuverswith apermitted phase at signalized intersections:empirical study in China[J].Journal of Transportation Engineering,Part A:Systems,2017,143(3):1-8.
[8]National Research Council(U.S.).HCM 2010:Highway capacity manual.5th ed[M].Transportation Research Board,2010.
[9]JANG J.Analysis of time headway distribution on suburban arterial[J].KSCE Journal of Civil Engineering,2012,16(4):644-649.
[10]曲昭伟,段宇洲,宋现敏,等.多车道环形交叉口车头时距分布模型[J].吉林大学学报(工学版),2015,45(3):740-747.[QU Z W,DUAN Y Z,SONG X M,et al.Analysis of time headway distribution models at multilane roundabout[J].Journal of Jilin University(Engineering and Technology Edition),2015,45(3):740-747.]

