考虑多因素的两类沉降预测方法比选

王志华

道路建设最基本的要求就是满足强度和稳定性。而表征道路整体稳定性的重要指标之一就是沉降量。沉降量的预测为施工时间、施工方案、后期营运养护提供相应的参数或者技术指标。沉降量的测定方法可以通过实验室测定，现场测定和相关经验来评估[1]。

目前，对于路基沉降预测的方法可分为两大类：①根据固结理论，结合土的本构模型计算最终沉降量，主要包括经典的分层总和法和各种数值分析方法，主要有限元法、差分法、无网格法和边界元法等[2]。这类方法的固结参数可能因样品干扰、样品大小和应变等因素而导致预测不准确。②数学拟合。目前，已有的路基沉降预测研究方法包括：沉降曲线拟合法（双曲线法、指数曲线法、泊松曲线法、三点法、S型曲线法等）；Asaoka方法；人工神经网络法；遗传算法；灰色预测法；有限元法等[3]。这类方法由于拟合中没有考虑土的本构模型，因此预测的准确主要依赖于实测沉降数据，而且路基沉降测量往往针对典型工点和局部地段进行量测，数据少、效率低且费用高[3～4]。因此，基于上述两种沉降预测方法在应用中存在的问题，本研究根据湘桂某道路沉降资料，利用PSO-ANN对路基沉降进行预测，试图为处理道路沉降提供技术依据。

1 PSO-ANN模型沉降预测

1.1 PSO-ANN方法简介

人工神经网络（ANN）是通过权重和偏差相互连接的神经元网络。一个典型的人工神经网络模型如图1所示。一旦人工神经网络的结构形成，下一个任务就是训练网络。

网络训练意味着找到网络中各种权重和偏差的最优值。通常，使用各种类型的技术来找到ANN的权重和偏差的合适值[5]。在本研究中，通过粒子群优化（PSO）获得了网络的最优训练。

图1 BP网络结构

PSO从这种模型中得到启示并用于解决优化问题。PSO中，每个优化问题的潜在解都是搜索空间中的一只鸟，称之为粒子。所有的粒子都有一个由被优化的函数决定的适值（fitness value），每个粒子还有一个速度决定它们飞翔的方向和距离。然后粒子们就追随当前的最优粒子在解空间中搜索[5～7]。

PSO初始化为一群随机粒子（随机解），然后通过迭代找到最优解[8]。在每一次迭代中，粒子通过跟踪两个极值来更新自己；第一个就是粒子本身所找到的最优解，这个解称为个体极值；另一个极值是整个种群目前找到的最优解，这个极值是全局极值。另外也可以不用整个种群而只是用其中一部分作为粒子的邻居，那么在所有邻居中的极值就是局部极值[8～9]。

假设在一个D维的目标搜索空间中，有N个粒子组成一个群落，其中第i个粒子表示为一个D维的向量：

第i个粒子的“飞行”速度也是一个D维的向量，记为：

第i个粒子迄今为止搜索到的最优位置称为个体极值，记为：

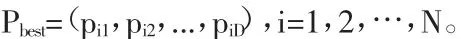
整个粒子群迄今为止搜索到的最优位置为全局极值，记为：

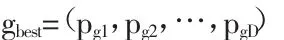
在找到这两个最优值时，粒子根据如下的公式（2.1）和（2.2）来更新自己的速度和位置：

其中：c1和 c2为学习因子，也称加速常数（acceleration constant），r1和r2为[0，1]范围内的均匀随机数[8]。由三部分组成，第一部分为“惯性（inertia）”或“动量（momentum）”部分，反映了粒子的运动“习惯（habit）”，代表粒子有维持自己先前速度的趋势；第二部分为“认知（cognition）”部分，反映了粒子对自身历史经验的记忆（memory）或回忆（remembrance），代表粒子有向自身历史最佳位置逼近的趋势；第三部分为“社会（social）”部分，反映了粒子间协同合作与知识共享的群体历史经验，代表粒子有向群体或邻域历史最佳位置逼近的趋势，根据经验，通常：c1=c2=2。i=1，2，…，D。vid是粒子的速度，vid=∈[-vmax，vmax]，vmax是常数，由用户设定用来限制粒子的速度。r1和r2是介于[0，1]之间的随机数[8]。

在借鉴传统BP神经网络的基础上，使用PSO对BP神经网络进行优化，依据以下7个步骤进行了训练：

步骤1：收集数据；

步骤2：创建网络；

步骤3：配置网络；

步骤4：初始化权重和偏差；

步骤5：使用PSO训练网络；

步骤6：验证网络：

步骤7：使用网络。

1.2 沉降值预测实例

本论文采用观测桩和沉降板两种方法对的某道路进行沉降观测，选取了2个测点的743个数据进行预测研究，由于数据较大，见表1。为了根据充填阶段预测沉降曲线，采用PSO-ANN法，首先选择分析参考阶段[10]。例如，如果在一个站点中使用了三个路堤构造阶段，那么参考阶段有三选择。然后，需要反映在场地特性中的土壤参数。这些数据可以从实验室和原位测试中获得。最后，需要一个粒子群安装状态。使用所有选定的数据、C1和C2计算，而Cc、Ch和F是通过PSO-ANN方法对被监视的沉降数据进行反分析所估计的值[3]。图2显示了PSO-ANN预测结果和真值和相关系数（左）及最小适应性曲线（右）。从该图可以看出，回归系数R为0.99353。

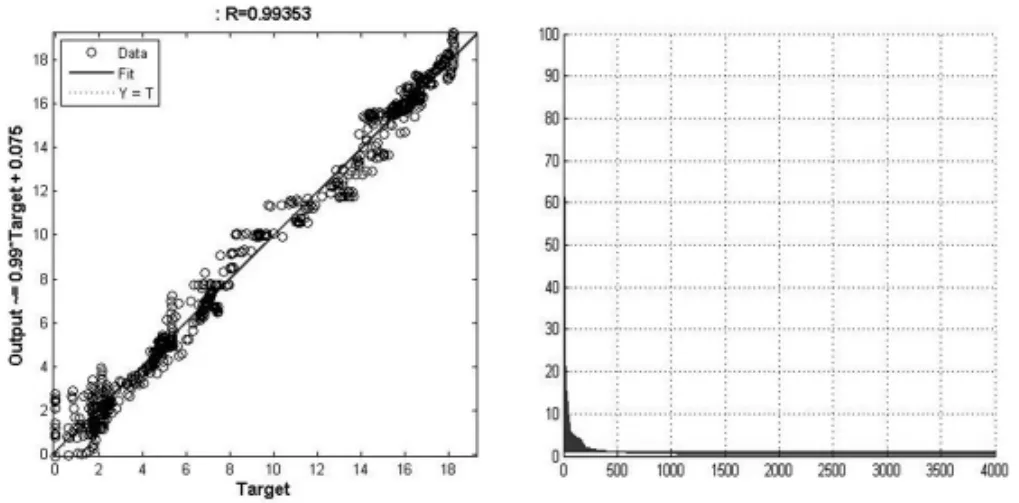
图2 PSO-ANN预测结果和真值和相关系数（左）及最小适应性曲线（右）

现在，使用训练好的神经网络可以用于知道未知输入特征的输出。让所述数据集的训练好的ANN的输入特征为test_input，其输出结果如下所示。

Calculation of MSE of total test data 0.438538.

实际上，test_input是从附表I取得的一组数据集，训练网络的输出（test_output） 结果显示：Calculation of MSE of total real data err_real=0.51151。若将该组数据中填筑阶段作为一组数据集，训练网络的输出（test_output） 结果显示：Calculation of MSE of total real nocomplete data err_realno=0.5548。若将该组数据中填筑完成阶段作为一组数据集，训练网络的输出（test_output）结果显示：Calculation of MSE of total complete real data err_realyes=0.2208。从结果可以看出，PSO-ANN模型对后期沉降预测较准确。

2 线性回归模型沉降量预测

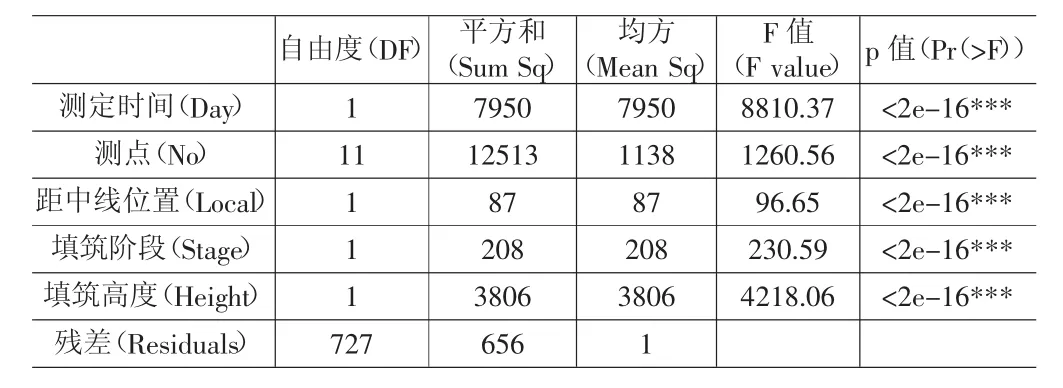
表1 沉降量实验方差分析结果

表2 沉降量实验线性回归分析结果

表1显示沉降量实验方差分析结果，测定时间（Day）、测点（No）、距中线位置（Local）、填筑阶段（Stage）、填筑高度（Height）四个因素对沉降量实验有显著性影响。将这四种因素和沉降量做回归分析，线性回归模型的均方误差（MSE）为0.9023855，随机选137个样本，线性回归模型的真值和预测值的MSE为1.237389。对照上面PSO-ANN模型，线性回归模型的均方误差约高1倍，由此可见PSO-ANN模型的预测准确性远远由于线性回归模型。

3 结束语

本文针对道路沉降预测问题展开研究，利用已监测的数据，采用PSO-ANN神经网络进行了研究，通过对比分析得出：PSO-ANN神经网络预测模型收敛速度更快和精度更高，验证了PSO-ANN神经网络预测道路沉降的有效性和可行性。该方法可通过Matlab计算，操作简单，通用性较强，能进一步提高沉降预测精度和收敛速度。本研究在两个断面、六个位点进行了现场沉降观测，通过现有预测方法、PSO-ANN的预测值和实际沉降量的对比，说明这种方法在沉降预测中的准确性。

[1]贺勇，诸克军，胡承凡.品位组合优化的粒子群-神经计算方法.系统管理学报，2010（02）：204～209.

[2]梁小丛，付金丹.基于PSO和ANN复合的边坡稳定性评价模型.山西建筑，2009（29）：114～115.

[3]张道法，陈涛.基于GA-PSO-ANN算法的隧洞岩土参数反分析.人民珠江，2015（06）：71～73.

[4]Chenglei H.，L.Kangji，L.Guohai，et al.Forecasting Building Energy Consumption Based on Hybrid PSO-ANN Prediction Model.in第三十四届中国控制会议.2015.中国浙江杭州.

[5]Feng X.，S.Li，C.Yuan，et al.，Prediction of Slope Stability using Naive Bayes Classifier.KSCE Journal of Civil Engineering，2018，22（3）：941～950.

[6]Koopialipoor M.，A.Fallah，D.J.Armaghani，et al.，Three hybrid intelligent models in estimating flyrock distance resulting from blasting.Engineering with Computers，2018：1～14.

[7]Lee S，I.ParkJ.-K.Choi，Spatial prediction of ground subsidence susceptibility using an artificial neural network.Environmental management，2012，49（2）：347～358.

[8]Tian H.，J.ShuL.Han，The effect of ICA and PSO on ANN results in approximating elasticity modulus of rock material.Engineering with Computers，2018：1～10.

[9]Li C.，A simplified method for prediction of embankment settlement in clays.Journal of Rock Mechanics and Geotechnical Engineering，2014，6（1）：61～66.

[10]张航，丁文霞.软土路基沉降观测点的布设.公路交通技术，2003（02）：13～14.