一种飞船用并联式太阳电池阵指向机构设计与分析

李 林，丁 健，孟庆平，王兴泽，王秀丽，裴 旭，吴跃民

（1.北京空间飞行器总体设计部，北京100094；2.北京航空航天大学机械工程及自动化学院，北京100191）

1 引言

太阳电池阵是飞船电源系统中的重要组成部分，在飞船飞行过程中需要依据其姿态和轨道进行角度调整，实现太阳光线与飞船太阳电池阵的最佳夹角，最大限度发挥太阳电池阵的效能［1］。目前飞船上太阳电池阵一般为单轴旋转［2］，优点是结构简单，但由于自身运动空间的限制，太阳光线不能始终与太阳电池阵垂直，不能完全实现光照效率最大化，同时更大面积的太阳电池阵带来更大的惯量负载，对飞船快速变轨调整有不利影响。太阳电池阵指向机构若具备3个自由度，即可满足其在轨的各种工作姿态需求。并联机构定位精度高、刚度大、结构稳定、承载能力强、运动惯量小、可冗余工作，在空间领域得到了越来越多的应用。

目前国际上综合性能较好的3自由度并联机构较少，CLAVEL［3］将4S平行四边形机构用于并联机构支链，设计出著名的3自由度移动机构DELTA；TSAI［4］等提出 3 自由度移动并联机构，支链用到了4R平行四边形机构。这类机构都可以归于含有闭环子链的并联机构，但组成复杂，运动学逆解较难，指向范围及工作空间较小，无法满足飞船太阳电池阵指向的大范围需求。NASA设计了一种新型并联机构，用于CEV反推发动机的指向与驱动，同时也可用于太阳电池阵指向装置，因为转动副采用销轴式方案，零部件采用异形连杆形式，存在加工难度大、运动精度差等缺点，且并未对其工作空间、运动学正逆解、冗余特性等进入深入研究［5］。法国国家空间研究中心研制了一种3自由度并联天线指向机构，用于空间高速数据传输探索项目，天线工作在X波段，目前已完成力学试验进入工程化阶段，由于机构构型原因，机构工作空间较小［6］。

本文提出一种具有3个自由度、采用模块化对称设计的新型并联式太阳电池阵指向机构方案，以满足太阳电池阵大范围指向需求，实现太阳电池阵光照效率的最大化，同时减小太阳电池阵惯性负载对飞船轨道机动的影响，丰富飞船太阳电池阵指向机构的选择型谱。

2 并联式太阳电池阵指向机构

目前飞船太阳电池阵一般为单轴旋转［2］，其运动范围受限于自身运动空间，要想实现光照效率最大化，就需要使太阳光线与太阳电池阵尽量垂直，一方面可以有效减少太阳电池阵面积需求，另一方面还可以随时调整太阳电池阵姿态以适应飞船各种任务需求。并联式太阳电池阵指向机构在设计时，需要重点考虑机械接口、电接口、控制接口等众多设计因素，本文在进行方案设计时，与相关设计部门对接了初步接口需求约束。

太阳电池阵在飞船上的姿态变化如图1所示，通过并联指向机构实现与飞船服务舱的连接，根据飞船的姿态及轨道需求，通过太阳敏感器确定最佳指向参数，通过反解计算实现太阳电池阵的实时对日指向调整。

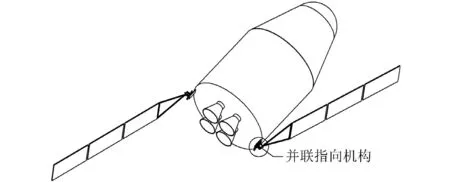
图1 太阳电池阵工作指向示意图Fig．1 Work diagram of the spacecraft solar array

并联指向机构的详细组成如图2所示，主要由定平台、动平台以及连接定动平台且均匀分布的3条支链组成一个闭环系统。其中3条支链采用模块化设计思想，采用完全相同的设计形式，包括两个短连杆、两个长连杆、连接各运动链的5个转动副。每个支链都通过单独的驱动组件驱动，驱动组件固定在基座上，其末端安装有高精度旋转编码器，用于输出角度的精确测量，通过三个驱动组件的运算配合，可实现动平台的大范围指向。动平台为太阳电池阵提供安装接口。旋绕式柔性电缆用于太阳电池阵电功率及电信号的传输，根据动平台的位置姿态自适应调整。

图2 并联式太阳电池阵指向机构Fig．2 Parallel pointing mechanism of the spacecraft solar array

3 运动学计算

并联指向机构由一个动平台Q1Q2Q3、三条支链PiGiQi（i＝1～3）和一个定平台 P1P2P3组成，两平台均为等边三角形，是一个典型的规则对称结构。整个机构由3条支链组成，每一个支链都有独立的驱动源，通过驱动源之间的运动算法，实现并联机构的大范围运动，运动过程中，机构相对平面ΔG1G2G3对称。

为了便于分析该并联机构的运动学正逆解，建立坐标系，如图3所示。定坐标系O-xyz及动坐标系C-uvw，原点O、C在两平台几何中心，x轴与矢量OP1重合，u轴与矢量CQ1重合。Pi-xiyizi（i＝1～3）固接在驱动关节上，坐标系Qi-uiviwi（i＝1～3）固接在被动关节上。 用 βi（i＝1～3）表示主动杆的输入角，用 αi（i＝1～3）表示矢量CQi与QiGi的夹角（即输出角）。设动平台 CQi＝ r（i＝1～3），定平台 OPi＝ R （i＝1～3），主动杆长度 PiGi＝ L1（i＝1～3），被动杆长度QiGi＝ L2（i＝1 ～3），进行正、逆解计算［7］。

图3 并联指向机构坐标系Fig．3 The coordinate system of parallel pointing mechanism

3.1 自由度计算

每个支链由5个转动副组成，如图4所示。其中转动副2、3、4等效为一个球副（S副），由Kutzbach Grubler公式［8］来表示该机构的自由度，如式（1）：

式中，F为机构的自由度；n为构件数；g为运动副数；fi为第i个运动副的相对自由度数。

由图4可知，机构中因为每个支链中有4个构件，则3条支链共12个构件，另外动、定平台共2个，因此机构共14个构件，所以n＝14。机构中有15个自由度为1的转动副，该机构无虚约束、局部自由度及复合铰链等特殊情况，所以g＝15。代入式（1）中，则有F ＝3。

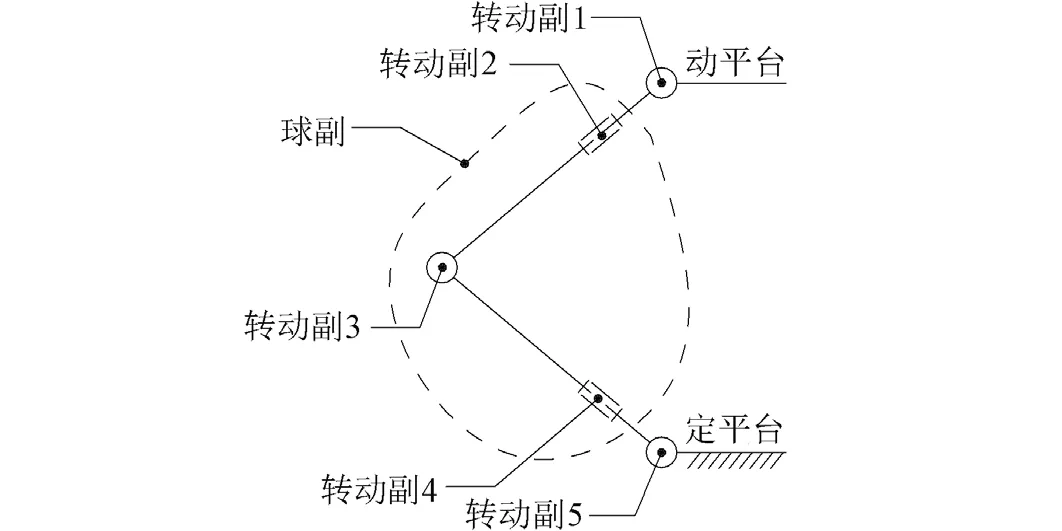
图4 单支链运动简图Fig．4 Single chain diagram of parallel pointing mechanism

3.2 运动学逆解

根据飞船太阳敏感器可得出实现最大光照效能的太阳电池阵目标位置，即得出动平台的目标位姿，反求并联指向机构的输入角度βi，即求出其运动学逆解，作为驱动组件的输出角度。

设独立变量为Xi＝ [Xc，Yc，Zc]T，φi为坐标系Pi-xiyizi相对定坐标系O-xyz的方位角，如式（2）：

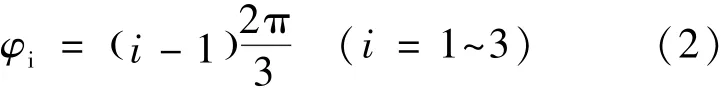
设oTPi表示坐标系Pi-xiyizi到定坐标系O-xyz的变换矩阵，如式（3）：

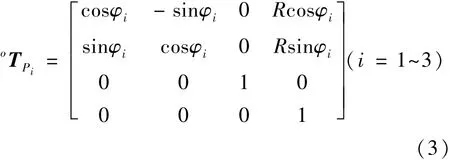
设PiGi表示Gi点在坐标系Pi-xiyizi的坐标，如式（4）：

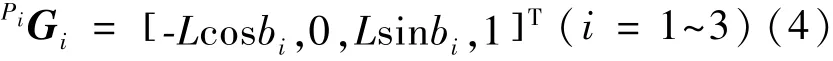
点Gi在定坐标系的坐标通过式（5）求得：

矢量OC被中间平面ΔG1G2G3平分且垂直于中间平面，设M点表示矢量OC与中间平面ΔG1G2G3的交点，如式（6）：

其中：M ＝OM，C ＝OC。

约束条件如式（7）：

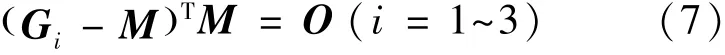
将式（5）和式（6）代入式（7）展开，可得到式（8） ～（11）：

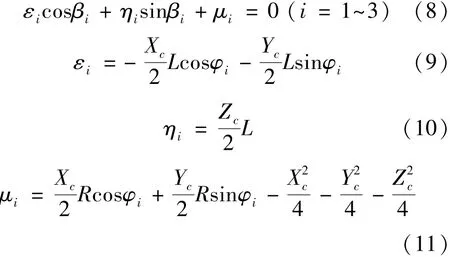
通过式（8）～（11），可求得并联指向机构的封闭逆解，即若给出工作空间 [ Xc，Yc，Zc]T， 即可得到驱动组件的输入角βi，每个βi都有两组值，因此有8组逆解，但8组逆解并非都适合并联机构的运行需求，还需对8组逆解进行筛选，确定其唯一性，以便控制系统方便实现驱动组件目标角度的输出。

3.3 运动学正解

并联机构的运动学正解一般较其逆解要困难得多，特别是当运动链增加时，并联机构的运动学正解很难得到封闭解，这往往会给并联机构的进一步研究带来困难［9］。但本文研究的空间3自由度并联指向机构关于面ΔG1G2G3规则对称，其正解较为简单。

若已知输入角度βi，则输出角度αi＝180oβi（i＝ 1～3），其正解唯一，根据逆解可知，假设点 M ＝ ［xm，ym，zm］T， 则 M 点满足式（12）：

其中，由公式（5）可计算出Gi，解该方程即可求出M点坐标，故C点坐标根据C＝2 M ＝［2xm，2ym，2zm］T解出，得到正解。

4 工作空间分析

并联结构的工作空间可分为可达工作空间和灵活工作空间［10－11］。对于空间并联机构来说，由于受其结构的限制，平台一般不能绕某一点转动360°，所以一般没有灵活工作空间，因此本文研究的工作空间指的是可达工作空间。

并联机构的工作空间受到主、被动杆的运动范围和连杆尺寸、结构等因素的限制，运用极限边界搜索方法［12］来计算工作空间较为方便。极限边界搜索方法是基于并联机构的运动学位置逆解而进行的一种搜索方法，即给出一个包含并联机构所有可能工作空间的范围，在此范围内，产生大量随机的点，每一点被测试是否在工作空间内，逐点求每一条支链的逆解，如果是实数解，该点就在工作空间内，否则在工作空间之外。若能将所有的满足约束条件的点搜索出来，那么由这些点所组成曲面构成了并联机构的工作空间。

本文使用MATLAB语言实现该算法，完成工作空间的搜索及可视化。经过优化设计，并联机构的结构尺寸R＝r＝84 mm，L1＝L2＝84 mm。 输入角度βi的变化范围为20°～180°，高度z变化范围为128 mm～328 mm。得到的工作空间如图5及图6所示，图中所示颜色即代表其数值大小，深蓝色数值最小，深红色数值最大。

图5 工作空间仿真图（三维）Fig．5 The 3D workspace of pointing parallel mechanism

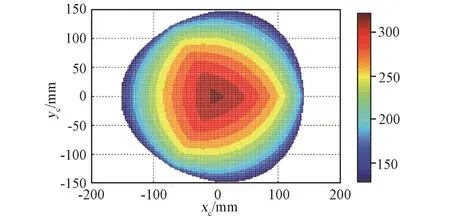
图6 工作空间仿真图（俯视）Fig．6 The top view of workspace of pointing parallel mechanism

5 仿真分析

5.1 运动学仿真

为验证正解、逆解的正确性，使用ADAMS进行运动学仿真。动平台C点的位置为目标位置，利用运动学逆解可求出三个输入角βi，每个βi都有两组值，通过组合可以得出8组逆解。由于并联指向机构中心安装有旋绕式柔性电缆，并联机构的3个支链运动不能与其产生干涉，因此必须对8组逆解进行筛选，确定其唯一性，以便控制系统方便实现驱动组件目标角度的输出。

为了寻找逆解的筛选规则，同时验证运动学逆解的正确性及精确性，建立基于ADAMS的虚拟样机，取虚拟样机的结构参数R＝r＝84 mm，L1＝L2＝84 mm，如图7所示。

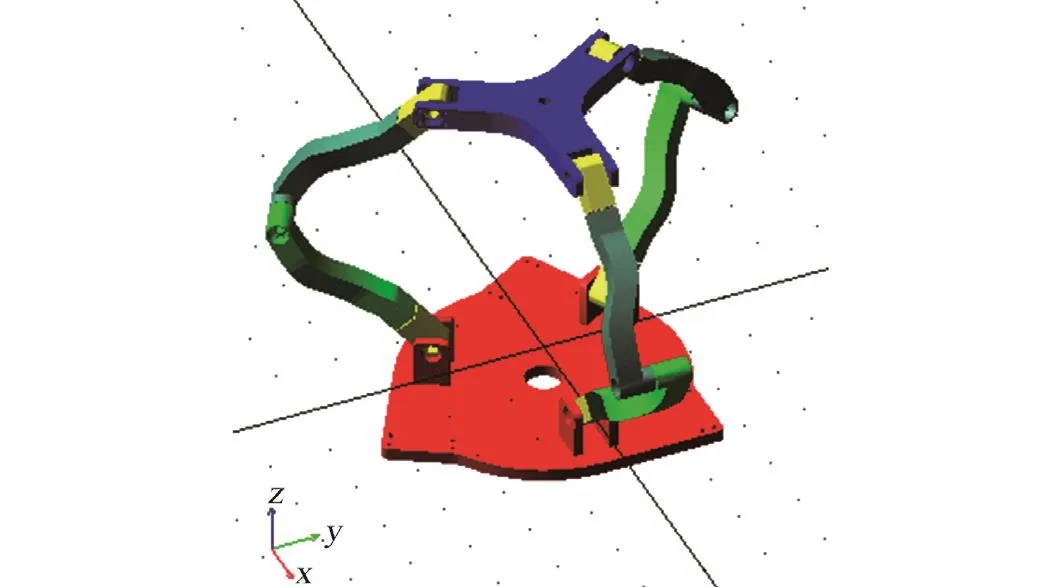
图7 虚拟样机模型Fig．7 The virtual model for simulation

取动平台 C点的位置 xc＝10 mm，yc＝20 mm，zc＝164 mm，在MATLAB中使用极限边界搜索法进行运行学逆解，计算出三个输入角βi：

对其8组逆解组合分别进行了仿真分析，本文列举了其中两组，其在ADAMS中的仿真状态如图8所示。

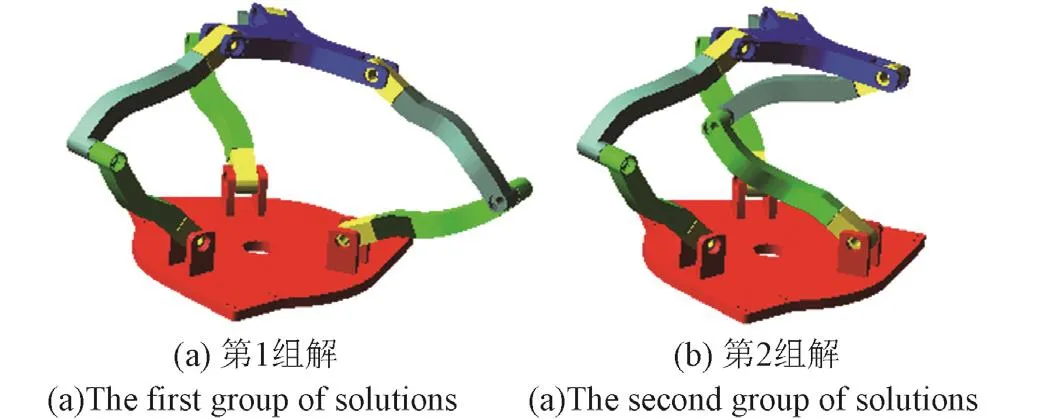
图8 虚拟样机运动学仿真Fig．8 The kinematics simulation of virtual model

由图8可知，第2组解得虚拟样机中有一个运动支链已明显进入旋绕式柔性电缆的区域内，存在干涉现象，其余的6组解同样存在该现象。通过对多组目标位置求解及仿真，只有当取输入角βi中两个解的最大值进行组合时，才能满足工程实现的需求，控制系统以此唯一逆解组合作为输出量。

把第1组逆解作为虚拟样机的输入角度，利用正解方法求动平台点C的位置，结果如图9所示。 图中，xc＝9.9999 mm，yc＝20.0000 mm，zc＝163.9999 mm。上述值与初始的目标位置误差较小，正解与逆解结果相互验证，证明了逆解计算的正确性。

图9 运动学仿真曲线Fig．9 The kinematics simulation curve

5.2 冗余特性仿真

当机构的某一个驱动失效时，该处的转动副变为失效卡死，但是机构仍然具有部分活动能力。通过运动学分析可以得出失效时的工作空间。例如，当一个驱动组件在β3＝135°的位置卡死时，工作空间仿真视图如图10、图11所示。

图10 β3＝135°卡死时的工作空间（三维）Fig．10 The 3D workspace when jammed at β3 ＝ 135°

对比图10与图5的工作空间视图，当某一驱动组件出现卡死失效时，并联机构仍具备约1／3的工作空间。

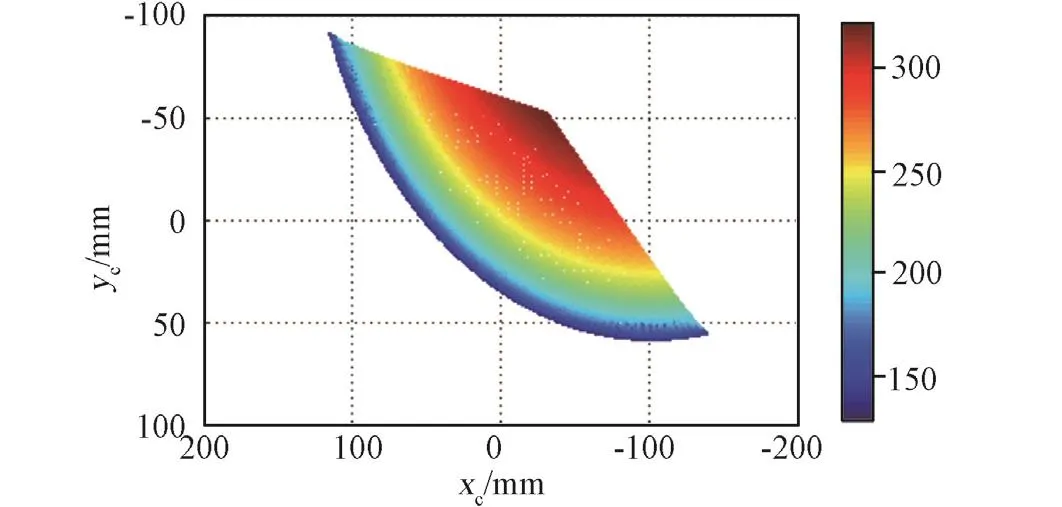
图11 β3＝135°卡死时的工作空间（俯视）Fig．11 The top view of workspace when jammed at β3＝135°

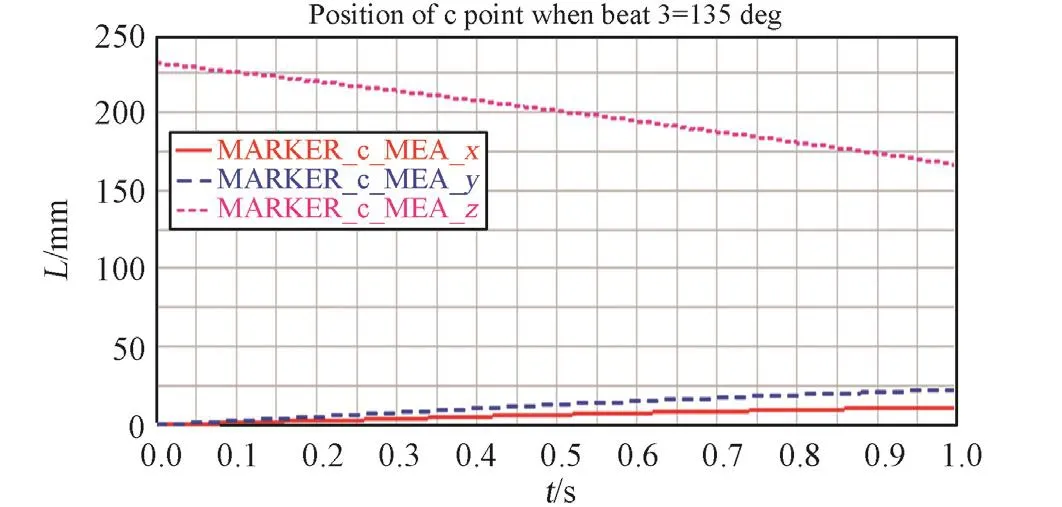
图12 β3＝135°卡死时点C最终位置Fig．12 The final position of C when jammed at β3＝135°

为了验证其冗余特性，将第5.1节中的第1组解代入ADAMS进行仿真，结果如图12所示。动平台 C点的目标位置为 xc＝10 mm，yc＝20 mm，zc＝164 mm，由仿真结果可知，当某一驱动组件卡死时，并联机构的最终位置为 xc＝11.57 mm，yc＝22.75 mm，zc＝167 mm，与目标位置相差不大，说明该并联指向机构具备较好的冗余特性。

6 结论

本文设计了一种飞船用新型并联式太阳电池阵指向机构，通过对其进行运动学正逆解计算及仿真分析，得出如下结论：

1）当目标姿态位置确定后，其输入角有8组逆解，只有一组解作为唯一合理解，即将每个输入角两个解中的最大值进行组合；

2）进行了运动学正解、逆解的相互验证，证明了正解、逆解的正确性；

3）当该并联机构中的某一驱动组件卡死时，机构仍具备较大的工作空间，最终位置接近目标位置，可靠性较高；

4）该并联式指向机构还可用于航天器矢量推进器、天线指向等空间领域。

参考文献（References）

［1］ 郗晓宁，吴瑞林，潘亮，等.载人航天器的发射窗口及太阳能帆板的最佳受晒［J］.中国空间科学技术，1997，17（5）： 54-60.Xi X N，Wu R L，Pan L，et al.The launching window of a manned spacecraft and the best exposure to solar panels［J］.Chinese Space Science and Technology， 1997， 17（5）：54-60. （in Chinese）

［2］ 谭维炽，胡金刚.航天器系统工程［M］.北京：中国科学技术出版社，2009：212-213.Tan W C， Hu J G.Spacecraft Systems Engineering［M］.Beijing： Science and Technology of China Press， 2009：212-213.（in Chinese）

［3］ Clavel R.Device for the movement and positioning of an element in space： United States Patent， 4976582［P］.1989-09-06.

［4］ Tsai L W，Walsh G C，Stamper R E.Kinematics of a novel three dof translational platform［C］ ／／Proc.of 1996 IEEE Int.Conf.on Robotics and Automation， Minneapolis， Minnesota，1996：3446-3451.

［ 5 ］ George Anwar， Liwei Lin.Robotic canfield joint［EB／OL］.http：／／canfieldjoint.com， 2010.

［6］ Lauren B，Nicolas R，Yann M.3POD：A high performance parallel pointing mechanism ［C］／／15th European Space Mechanisms＆ Tribology Symposium，Noordwijk，the Netherlands D.C.：ESMATS， 2013.

［7］ 黄真，赵永生，赵铁石.高等空间机构学［M］.北京：高等教育出版社，2006：141-166.Huang Z， Zhao Y S， Zhao T S.Advanced Spatial Mechanism［M］.Beijing： Higher Education Press，2006：141-166. （in Chinese）

［8］ 梅莱.并联机器人［M］.黄远灿，译.北京：机械工业出版社，2014：10-11.Mei L.Type Synthesis of Parallel Mechanisms［M］.Huang Y C， translated.Beijing： China Machaine Press， 2014： 10-11.（in Chinese）

［9］ 刘辛军，汪劲松，李剑锋，等.一种新型空间3自由度并联机构的正反解及工作空间分析［J］.机械工程学报，2001， 37（10）： 36-39.Liu X J， Wang J S，Li J F，et al.Direct and inverse kinematics and workspace analysis of a new typeof space 3DOF parallel mechanism［J］.Journal of Mechanical Engineering，2001，37（10）： 36-39. （in Chinese）

［10］ Kumar V.Characterization of workspaces of parallel manipulators［J］.ASME J.Mech.Des.1992a， 114： 368-358.

［11］ Kumar V.Instantaneous kinematics of parallel chain robotic mechanisms［J］.J.Mech.Des.1992b， 114： 349-358.

［12］ 胡福生，郝秀清，陈建涛.3PSS并联机构的运动学分析［J］.山东理工大学学报（自然科学版），2006， 20（1）：43-46.Hu F S，Hao X Q，Chen J T.Kinematics analysis of 3PSS parallel mechanism ［J］.Journal of Shandong University of Technology（Sci＆Tech），2006， 20（1）：43-46. （in Chinese）