一种以燃耗为优化目标的航天器在轨加注作业调度

谭迎龙，乔 兵∗，朱啸宇，靳永强，张庆展

（1.南京航空航天大学航天工程系，南京210016；2.上海交通大学航空控制科学与工程系，上海200240；3.上海宇航系统工程研究所，上海201109）

1 引言

随着航天技术的快速发展，在轨航天器的数量逐渐增多，导致空间资源日趋紧张。同时，技术的进步使航天器携带设备发生故障的概率大幅度下降，燃料的限制已成为制约航天器长期在轨的主要因素［1］。因此，各航天大国纷纷提出“航天器在轨加注”的设想以加强在轨航天器的机动能力和工作寿命［2］，并在此基础上进行了多次“一对一”航天器在轨加注的验证性实验，实验证明在轨加注可行性的同时，也表明进行“一对一”在轨加注其成本往往比更换一颗新航天器还高［3］。为了获得更好的效费比，一颗服务航天器对多颗目标航天器进行加注的“一对多”在轨加注模式被提出［3］。研究表明，“一对多”在轨加注模式优于“一对一”在轨加注模式，因此，“一对多”模式必将会成为主流的研究方向［3-4］。随着目标航天器数量的增加，在有限的时间内，一颗服务航天器将无法完成整个在轨加注任务，因此根据任务的需要，多颗服务航天器将会同时进行各自的“一对多”在轨加注任务，此时的在轨加注模式便称为“多对多”加注模式［3］。

地球静止轨道（Geostationary Orbit，GEO）运行着预警、通信及中继卫星等大量高价值航天器，并且由于此类航天器的大量发射导致GEO轨道资源稀缺，且此类航天器主要运行在GEO带附近，分布集中。因此，GEO航天器比较适合作为在轨加注目标航天器。为了给“一对多”和“多对多”在轨加注试验实施提供理论基础，已经有学者对其展开了相关的研究，欧阳琪［3］对地球同步轨道卫星群在轨加注任务规划问题进行了研究，成功地将在轨加注问题转化成TSP问题求解。Shen等［5-6］解决了基于多圈Lambert问题的最优双脉冲问题，指出“一对多”在轨加注调度的目的是找到总燃耗最小的最优加注服务顺序以及最佳时间分配方案，最优服务顺序总是在一些总扫描角最小的序列中。在文献［6］的基础上，Shen 等［7］又研究了三种不同的在轨加注模式，研究表明混合P2P加注模式有更少的燃料消耗量。Zhou等［8］对基于燃料站的“一对多”加注模式的在轨加注任务规划问题进行了研究，结果表明最优加注顺序是按目标航天器真近点角位置依次加注。

本文将在传统“多对多”在轨加注模式的基础上引入一个空间燃料站，构成一个拥有目标航天器（Target Spacecraft， TS）、服务航天器（Servicing Spacecraft， SSc）和空间燃料站（Propellant Depot，PD）的在轨加注网络系统，为了叙述方便，该加注网络系统所形成的加注模式称为“k-1-n”模式。同时，将基于“k-1-n”模式，考虑任务时间限制、航天器携带燃料量限制以及目标航天器所需燃料的不同，开展对GEO轨道航天器在轨加注任务调度问题的研究。

2 数学模型

2.1 问题描述

基于空间燃料站的“多对多”在轨加注模式如图1所示，空间部署着三种航天器。在燃料站轨道（Obrit1）部署着一个空间燃料站，在加注任务开始前k颗服务航天器与空间燃料站处于对接状态，其作用是负责把空间燃料站的燃料输送给目标航天器。n颗目标航天器位于GEO轨道，各目标航天器之间有一定的相位差。当目标航天器提出加注需求，在规定的时间内，服务航天器进行轨道机动，对目标航天器进行加注作业，当服务航天器的燃料不足以完成加注任务时，服务航天器可在任务中途返回燃料站获取燃料后继续进行加注任务。服务航天器完成所有目标航天器的加注作业后需返回空间燃料站，等待下一次的加注任务，在无加注任务的时间，服务航天器将从空间燃料站进行燃料补给，为下次加注任务做准备。

图1 “k-1-n”在轨加注模式示意图Fig．1 Diagram of k-1-n on-orbit refueling strategy

2.2 模型分析

本文的共面圆轨道转移将采用多圈Lambert轨道转移，并参考文献［5］的研究成果优化轨道转移的时间分配方案。当r1＝r2时，即目标航天器与服务航天器同处于GEO轨道，在求得初始真近点角差后，便能求解多圈Lambert轨道转移过程中最小速度增量和转移时间的关系，如图2虚线所示，初始真近点角差θ＝60o。两者的关系并不递减，但极小值点呈现逐渐减小的趋势，文献［5］利用这一特点，采用轨道转移末端滑行的方法，使最小速度增量与转移时间呈现出递减的关系，近似阶跃函数，如图2实线所示，可知在一段时间内燃料消耗量是不变的。因此，可用一个整数作为该时间区间的索引号，定义Index＝a表示第a个时间区间，如图3所示，故可将对转移时间的优化转化成对转移时间区间索引号的优化。

图2 最小速度增量和转移时间的关系［5］Fig．2 Relationship between the minimum speed increment and transfer time［5］

图3 最小速度增量和转移时间关系（定义索引号）Fig．3 Relationship between the minimum speed increment and transfer time（with index）

对于加注任务而言，完成任务的时间越短越好，因此，在给定时间区间索引号后，选择该区间最小的转移时间作为轨道转移时间的解。

当r1≠r2时，多圈Lambert轨道转移过程中，最小速度增量与转移时间关系的极小值并未呈现出逐渐减小的趋势，无法采用滑行的手段将两者变换成递减的关系，故不能采用处理r1＝r2的方法处理r1≠r2的情况。因此，该条件下轨道转移所需速度增量与转移时间取两者关系的第一个极小值点。

2.3 优化模型

航天器在轨加注服务系统中服务航天器的数量为 k， 序号集合为 S ＝ ｛s1，s2，…，sk｝，si的最大燃料携带量为 Qi，其中 i＝ 1，2，…，k；目标航天器的数量为n，序号集合为 X ＝ ｛x1，x2，…，xn｝，xj的燃料需求量为 fj，j ＝ 1，2，…，n ；燃料站的数量为1，其序号为x0。服务航天器需要在时间内完成对所有目标航天器的加注作业。

“k-1-n”在轨加注系统拥有k颗服务航天器，因此可将整个在轨加注任务分成k个子任务讨论，即第i个子任务为si所执行的加注任务。因此，需对子任务进行优化，使在轨加注总任务用于轨道转移的燃耗最小。设计优化变量Ji、Ai，如式（1）：

式中：Ji为si的加注目标和加注顺序，如J1＝［1，2，3］，表示s1需要加注的目标航天器序号为 x1、x2、x3， 加注顺序为： x1→ x2→ x3；Ai为si执行对应目标航天器加注作业所分配的轨道转移时间区间索引号。

服务航天器si在对目标航天器执行加注作业的过程中可能出现两种情况：第一种为si在执行对1的加注作业后，由于燃料的限制，无法完成对的加注作业，需返回燃料站补充燃料后再机动至为其加注；第二种为si在执行对的加注作业后，有充足的燃料完成对的加注作业无需返回燃料站。因此，si在完成对的加注作业后，需要根据服务航天器的燃料剩余量与完成对执行加注作业燃料需求量的关系对的加注作业进行评估。评估策略如下：当满足式（2）时， si在完成的加注作业后无需返回燃料站进行燃料补充，该情况下设决策变量＝ 0，si为执行加注作业是从燃料站出发，故＝0。

即si用于轨道转移的时间ti＝ ［，…，，tlii＋1］， 其中，tlii＋1为si完成任务后返回燃料站的轨道转移时间。完成任务的总用时Ti和轨道机动的燃料消耗量分别如式（10）、式（11）所示：

以轨道转移燃耗为优化目标的航天器在轨加注任务调度问题考虑三类约束条件，第一类为加注关系约束，在加注任务中一颗目标航天器只能被服务一次，且每颗目标航天器都要被服务。因此，加注关系约束如式（12）所示：

第二类约束为时间约束，根据加注任务的要求，服务航天器必须在规定的时间内完成加注任务，且为了考虑工程实际，需要对每次轨道转移时间进行最大值约束［8］，时间约束如式（13）、式（14）所示：

式（14）中，tmax为允许的最大转移时间。

第三类约束为燃料约束，服务航天器的燃料需求量需小于服务航天器的最大燃料携带量，燃料约束如式（15）所示：

对于整个在轨加注任务而言，用于轨道机动所消耗的燃料越少越好。所以，本文将通过优化Ji和Ai，在满足约束条件的前提下，使整个加注任务轨道机动的燃料消耗量最小化。在轨加注任务的数学模型如式（16）所示：

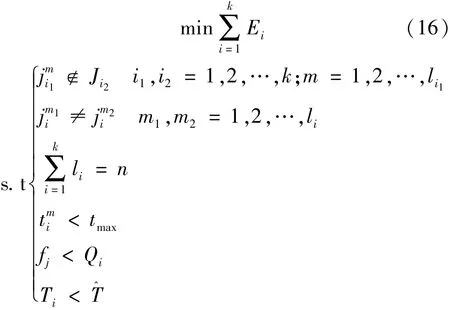
3 问题求解

基于“k-1-n”模式的在轨加注调度问题属于整数规划问题。该调度问题与车辆路径问题（Vehicle Routing Problem，VRP）和作业车间调度问题（Job-shop Scheduling Problem，JSP）等具有相似性，遗传算法对于此类问题的求解具有较强的优势。因此，本文将采用遗传算法求解在轨加注调度问题。

3.1 遗传算子设计

1）编码

染色体基因分为两段，顺序段基因J和时间段基因 A， 其中 J ＝ ［0，J1，0，J2，0，…，0，Jk，0］，AA ＝ ［A1，A2，…，Ak］ 。

2）选择

本文采用随机遍历抽样法（Stochastic Universal Sampling，SUS）进行选择。对于染色体适应度的计算取燃料消耗量的倒数。

3）交叉

染色体包含顺序段和时间段，由于两段染色体存在差异，所以进行交叉操作时分为顺序段和时间段。

顺序段基因的交叉方式为随机选取两个交叉位，保留杂交位外的基因，再搜索交叉位中间的基因是否为0，如果为0，则保留相应基因位上的基因，如果不为0，则交换相应基因位的基因。在交叉后对顺序段染色体进行基因去重操作。

时间段基因由于没有基因值不一样的约束，因此交叉方式为随机选取两个基因位，将基因位中间的基因串交换。

4）变异

顺序段基因的变异方式为随机选取两个需要变异的基因位，将两个基因位上的基因互换。

时间段基因的变异方式为随机选取一个基因位，将该基因位为上的基因换成其它合法值。

3.2 算法流程

采用遗传算法求解在轨加注任务调度问题的算法流程如图4所示。首先确定每个子任务的分配方案，即确定每颗服务航天器的加注目标、加注顺序以及每次轨道转移所分配的时间，初始化种群。然后服务航天器按任务分配方案执行加注作业，在每次加注作业的初始时刻需对此次加注作业进行评估，当服务航天器燃料不足时需返回空间燃料站补充燃料，直至所有目标航天器都被加注。最后更新子任务分配方案，在找到最优分配方案后，输出结果。

图4 k-1-n模式在轨加注任务调度算法流程图Fig．4 Algorithm flowchart for k-1-n on-orbit refueling strategy

4 算例

4.1 问题配置

选取14颗GEO卫星作为目标航天器，卫星的轨道根数如表1所示（数据参考文献［5］和文献［6］）。目标航天器所需要的燃料分别为［260，240，230，270，230，200，240，220，270，280，210，230，240，230］，单位为 kg。 燃料站轨道半径为39 164 km，初始真近点角为0°；服务航天器的数量为2，两颗服务航天器的干重均为500 kg，最大燃料携带量为1500 kg，初始时刻燃料携带量为1500 kg，推进系统比冲300 s。设服务航天器为单个目标航天器进行加注时加注操作时间为1 d，从燃料站获取燃料的操作时间为1 d，规定的任务总时间约束为40 d，设置遗传算法的种群规模为100，迭代代数为200，交叉概率为 0.9，变异概率为0.1，代沟为0.9。

4.2 近似最优解

根据给出的条件，遗传算法经过200次的迭代后（如图5所示），获得近似最优解。服务航天器s1用于轨道转移的燃耗为156.1400 kg，完成任务的时间为39.1694 d，加注目标及加注顺序为［x9，x11，x13，x1，x2，x4，x14，x6，x8］， 每次轨道转移燃耗和转移时间如表2所示。服务航天器s2用于轨道转移的燃耗为108.9544 kg，完成任务的时间为22.5938 d，加注目标及加注顺序为 ［x3，x10，x12，x5，x7］，每次轨道转移燃耗和转移时间如表3所示。

表1 GEO航天器的轨道根数［5-6］Table 1 Orbit elements of GEO spacecraft［5-6］

图5 遗传算法优化过程Fig．5 Optimization process of genetic algorithm

表2 服务航天器s1的轨道转移燃耗和时间Table 2 Consumption of fuel and time for servicing spacecraft s1

表3 服务航天器s2的轨道转移燃耗和时间Table 3 Consumption of fuel and time for servicing spacecraft s2

对问题求解获得决策变量 α1＝ ［0，0，0，0，0，1，0，0，0］，α2＝ ［0，0，0，0，0］。 所以服务航天器s1在对目标航天器x4执行加注作业的过程中需返回空间燃料站补充燃料。服务航天器在轨加注顺序示意图如图6所示。

图6 服务卫星加注示意图Fig．6 Diagram of servicing spacecraft refueling

4.3 结果分析

从实验结果可知，服务航天器在返回空间燃料站补充燃料前的最优加注顺序是按一种真近点角位置依次加注的顺序，当服务航天器返回空间燃料站后的加注顺序不再完全符合这种规律。这主要是所有目标航天器处于同一圆轨道，服务航天器按照真近点角位置依次加注，轨道转移的燃耗最小，这一结果与 Zhou［8］等的结论一致。但是，空间燃料站与目标航天器运行在不同高度的共面圆轨道上，服务航天器在执行加注任务的过程中需往返燃料站补充燃料，导致空间燃料站与目标卫星的真近点角差会发生变化，改变服务航天器的下一个最优加注目标。并且根据仿真计算数据可知，不同半径圆轨道间的轨道转移所需的燃料大于同轨间轨道转移所需的燃料，为了减小服务航天器往返空间燃料站的燃耗，需要考虑空间燃料站与目标航天器的真近点角差，而非只考虑目标航天器之间的真近点角差，致使服务航天器的最优加注顺序不再符合最优加注顺序规律。同时，轨道转移的燃耗与目标航天器的质量成正比，当某颗目标航天器的燃料需求量相对于其它目标足够大时，其将会有较高的优先级。

5 结论

1）在轨加注调度问题与VRP、JSP等调度问题有着较高的相似度，因此可以借鉴VRP、JSP的求解方法解决在轨加注调度问题。

2）以14颗GEO卫星作为加注对象，运用遗传算法求解结果证明，利用求解VRP与JSP的方法求解在轨加注作业调度问题具备可行性。

3）“k-1-n”在轨加注任务调度问题模型的建立以及问题的求解可为后续解决“k-m-n”在轨加注问题提供基础，甚至可在此基础上进一步分析带时间窗口等约束条件的在轨加注问题。

参考文献（References）

［1］ 林巧.GEO航天器在轨燃料补给任务调度及优化［D］.南京：南京航空航天大学，2016.Lin Q.Optimal Scheduling of On-orbit Refuelling for GEO Spacecraft［D］.Nanjing：Nanjing University of Aeronautics and Astronautics， 2016.（in Chinese）

［2］ 朱啸宇，乔兵，张庆展，等.一种基于空间燃料站的GEO航天器在轨加注任务调度算法［J］.工程科学与技术，2017，49（增刊1）：186-194.Zhu X Y，Qiao B，Zhang Q Z，et al.A reusable on-orbit refueling mode and mission scheduling algorithm for GEO spacecraft through a space fuel station ［J］.Advanced Engineering Sciences， 2017，49（Supp.1）： 186-194.（in Chinese）

［3］ 欧阳琦，姚文，陈小前.地球同步轨道卫星群在轨加注任务规划［J］. 宇航学报，2010，31（12）：2629-2634.Ou Y Q，Yao W，Chen X Q.Mission Programming of on-orbit refueling for geosynchronous satellites ［J］.Journal of Astronautics， 2010， 31（12）： 2629-2634.（in Chinese）

［4］ Tsiotras P， Nailly A.Comparison between peer-to-peer and single spacecraft refueling strategies for spacecraft in circular orbits［C］／／Proceedings of the 2005 Infotech ＠ Aerospace Conference.Arlington：American Institute of Aeronautics and Astronautics， 2005： 26-29.

［5］ Shen H， Tsiotras P.Optimal two-impulse rendezvous using multiple-revolution Lambert solutions ［J］.Journal of Guidance， Control， and Dynamics， 2003，26（1）：50-61.

［6］ Shen H.Optimal Scheduling For Satellite Refuelling In Circular Orbits ［D］.Georgia Institute of Technology，2003.

［7］ Shen H，Tsiotras P.Peer-to-Peer refueling for circular satellite constellation ［J］.Journal of Guidance， Control， and Dynamics， 2005， 28（6）： 1220-1230.

［8］ Zhou H，Yan Y，Huang X，et al.Multi-objective planning of a multiple geostationary spacecraft refuelling mission ［J］.Engineering Optimization， 2017， 49（3）： 531-548.