基坑开挖卸荷引起立柱桩的隆起位移计算

操小兵 金 文 李镜培,* 姚建平

(1.同济大学岩土及地下工程教育部重点试验室,上海 200092; 2.同济大学地下建筑与工程系,上海 200092;3.上海南汇建工建设(集团)有限公司,上海 201399)

0 引 言

工程实例表明,当桩基优先于基坑开挖施工时,基坑开挖使桩身轴力发生明显变化,使桩基处于受拉状态[1]。基坑开挖卸荷引起坑底土体产生回弹隆起,对立柱桩产生向上的上拔力,过大的上拔力使桩身出现较大的拉应力,不仅可能使桩身拉断或者开裂,而且上拔力引起的立柱桩竖向位移可能对基坑围护结构的稳定性产生不利影响。因此有必要对基坑开挖过程中坑底回弹引起的立柱桩位移及相关桩-土相互作用机理展开研究,以期为基坑开挖过程中立柱桩的位移和受力计算提供必要的理论依据,具有重要的现实意义和理论价值。

基坑坑底土体隆起对桩的作用与膨胀土对桩的作用相似,Poulos等[2]采用弹性理论法,通过假定膨胀量随深度的分布来分析膨胀土回弹隆起对桩的影响。楼晓明[3]基于广义荷载传递法,在考虑桩间土附加荷载与变形的基础上提出了深基坑开挖过程中立柱桩位移的计算分析方法,但未考虑基坑支撑体系的约束作用和坑底加固作用。贺翀[4]考虑了土体回弹深度,通过Mindlin求解计算土体的回弹量,分析了立柱桩桩长大于和小于回弹影响深度两种情况下立柱桩的隆起值,但未考虑桩身与桩侧土体的变形协调作用。除以上研究以外,其他多数研究[5-7]采用有限元方法模拟分析基坑开挖引起的立柱桩位移规律,但因立柱桩竖向隆沉问题的力学机理比较复杂,与场地地层特性、基坑开挖方式、支撑类型和支撑道数等众多因素有关,从有限元物理力学参数取值到计算量来看,目前难以广泛应用于立柱桩位移分析。

基坑开挖过程中立柱桩的竖向位移是基坑坑底土体隆起与上部支撑和围护结构共同作用的结果。然而,基坑开挖过程中,立柱桩是上抬还是下沉尚缺少比较实用的计算公式,实际工程中只能依靠施工中的监测数据来判别。基于此,本文从桩土的相互作用机理出发,分别考虑土体回弹对立柱桩上拔作用和支撑围护结构对立柱桩的约束作用,基于剪切位移法提出了立柱桩竖向位移和荷载传递规律的理论分析方法,分析了基坑开挖过程中立柱桩的位移规律,为解决开挖卸荷引起立柱桩隆起位移的计算提供了一定的理论依据。

1 立柱桩与坑底土体相互作用分析

基坑开挖后坑底土由于卸荷打破了原有的平衡状态,卸荷后土体会回弹隆起,对立柱桩产生上拔作用。通过对后文工程实例实测数据分析,提出以下两点假定:

假定1:假定每步开挖为一个瞬时过程,立柱桩在开挖过程中保持相对静止的平衡状态,当开挖到达一定深度后,立柱桩在土体回弹和上部支撑的双重作用下重新开始变形协调,重新达到平衡状态。因此每一步开挖可以看作一次重新变形协调,立柱桩每步的累积位移即为立柱桩最终的隆起位移。

假定2:通过平衡条件可知,桩因土体回弹引起的隆起量小于基坑开挖过程中土体的实际回弹量,因而假定立柱桩发生隆起位移的深度小于土体回弹深度。

1.1 桩顶荷载作用下桩的竖向位移

如图1所示,桩周土体的竖向位移ws1(r,z)与深度z和距离桩的径向距离r有关,根据文献[8],可知,ws1(r,z)随着r的增大呈对数递减的规律。

图1 桩侧土的竖向位移随径向距离的变化Fig.1 The vaviation of vertical displacement of soil beside soil with radial distance

(1)

式中,f1(z)为竖向位移函数;rm为桩周土体的最大影响半径,一般rm=2.5L(1-vs),L为桩长,vs为土体泊松比。

桩土界面处wp1=ws1,满足竖向位移协调,则有:

(2)

式中,wp1(z)为桩顶荷载作用下桩的竖向位移;ζ为桩径的影响因子,其中ζ=ln(rm/r0),r0为桩的半径。

将式(2)代入式(1)有:

(3)

忽略径向位移的影响,由弹性理论可得土中的剪切应力为:

(4)

当r=r0时,即为桩侧摩阻力:

(5)

式中,Gs为桩侧土体的剪切模量。

对桩端下卧层,在桩端荷载Pb1作用下,根据Boussinesq理论可以求出该处的土体的竖向位移为wb1=nbpb1,其中nb=η(1-μb)/4rbGb,η为桩端影响因数,一般取η=0.5～1.0,μb为桩端土体泊松比,rb为桩端半径,Gb为桩端土体剪切模量,wb1为桩端土体位移。

根据荷载传递法,将桩划分为许多个弹性单元,每个单元与土体之间采用非线性弹性元相接连,来模拟桩土相互作用,如图2所示。由任一微段dz的竖向平衡条件可得:

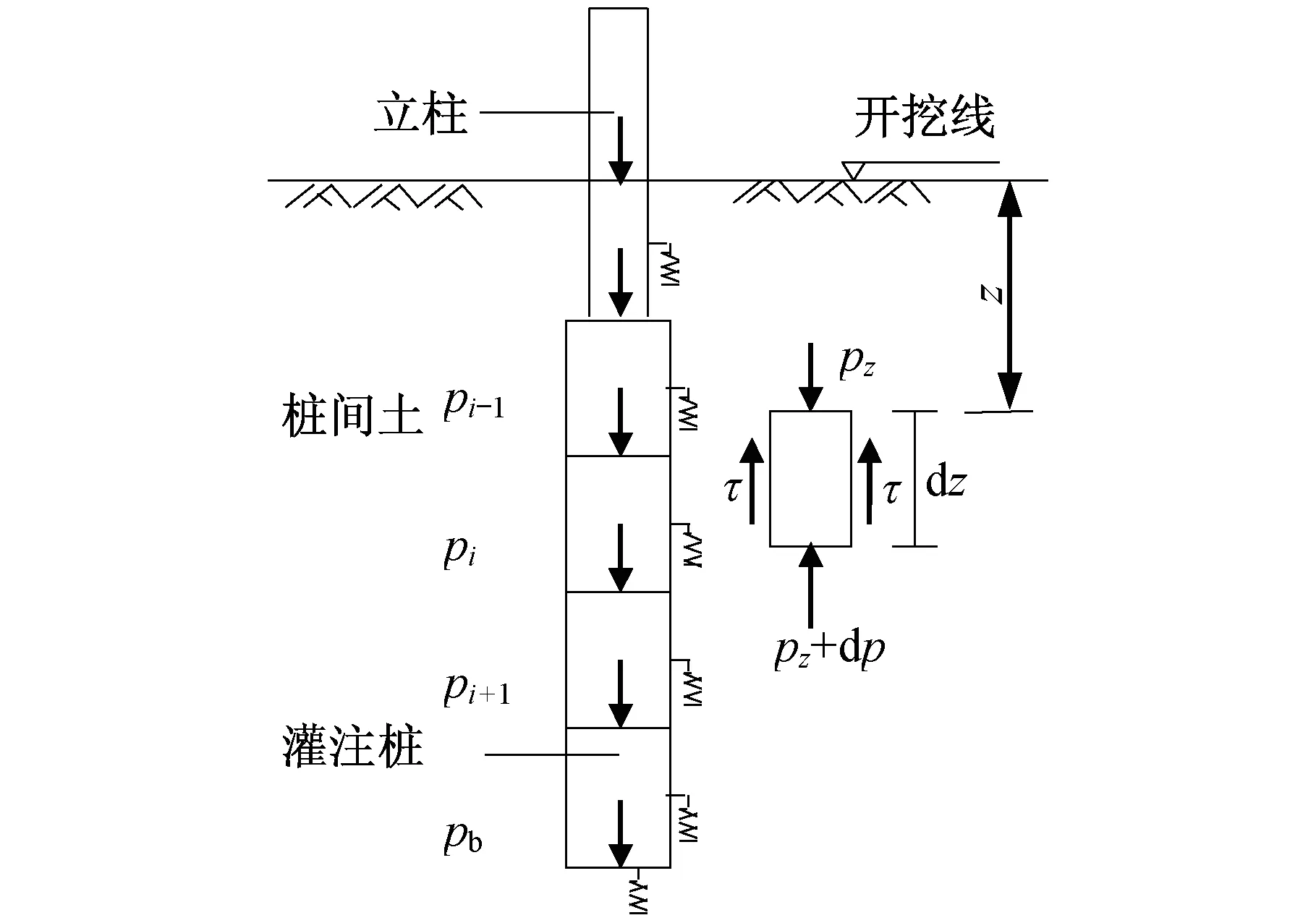
图2 桩-土共同作用模型Fig.2 Pile-soil interaction model

dp1(z)=-2πr0τ1dz

(6)

式中,p1(z)为桩顶荷载作用下桩深z处的轴力,桩身位移与轴力存在如下关系:

(7)

式中,EP为桩的弹性模量;AP为桩的横截面面积。

对式(7)求导,联立式(6)可得式(8):

(8)

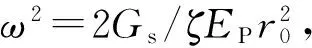
wp1(z)=c1sinh(ωz)+c2cosh(ωz)

(9)

式中,c1和c2为积分常数。

有边界条件z=0时,p(z=0)=pp;p(z=L)=wp1(L)/nb。确定c1和c2后,代回式(9)可得:

(10)

式中,α=ωL,n=EpApωnb,θ=1-z/L。

1.2 土体回弹引起桩的竖向位移

桩周土在回弹作用下,一方面由于地基土回弹使桩产生上拔位移,另外一方面,桩侧摩阻力作用将阻止桩周土体回弹。根据桩-土相互作用机理,假定桩周土位移为[9]

ws2(r,z)=f2(z)ln(rm/r)-S(z)

(11)

式中,S(z)为z深度处rm以外的土的回弹量;f2(z)为与深度有关的竖向位移函数。

桩-土界面ws2=wp2,满足竖向位移协调,则有:

(12)

忽略径向位移的影响,由弹性理论可得土中的剪切应力为

(13)

当r=r0时,即为桩侧摩阻力:

(14)

在土体回弹的作用下,桩-土共同作用模型如图3所示,此时桩顶没有荷载只有基坑隆起,桩端无反力作用,因此土相对于桩产生向上的位移,桩侧产生负摩阻力。

根据桩身任意单元的受力平衡条件可得:

dN2(z)=-2πr0τ2dz

(15)

式中,N2(z)为土体回弹膨胀作用下桩身深度z处的轴力;τ2是桩身z深度处的桩侧负摩阻力。

根据胡克定律由单元体产生的弹性压缩为:

(16)

对式(16)求导,代入式(15)中可得:

(17)

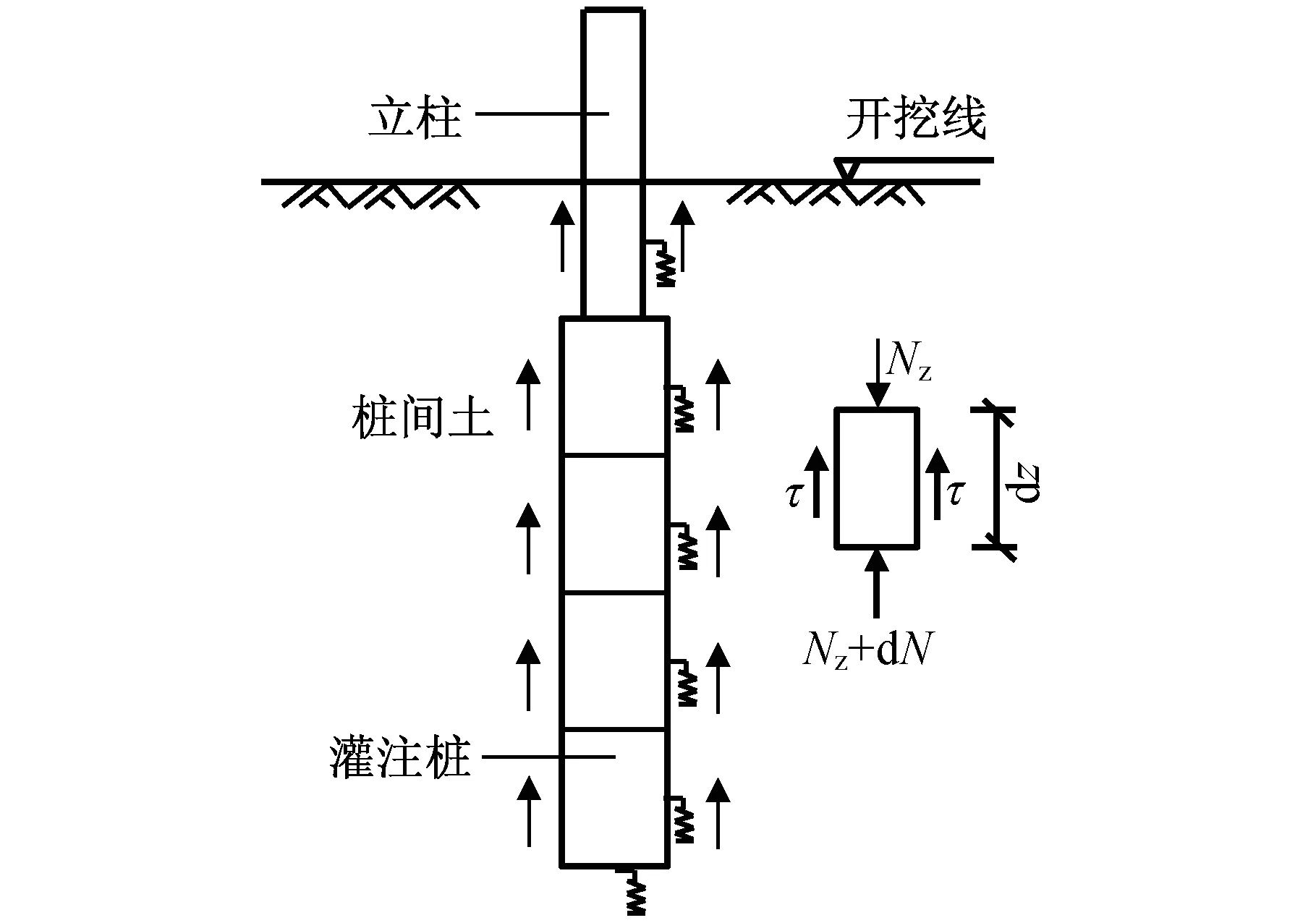
图3 土体回弹作用下的桩-土共同作用模型Fig.3 Pile-soil interaction model under the action of soil rebound

式中,μ2=2πGs/ζEPAp。

根据文献[3],对于开挖深度为H的基坑,坑底以下土体回弹应力随深度呈近似线性衰减的关系,即:

Δσrz=αzpc-γ′z

(18)

式中,Δσrz为坑底回弹应力;αz为弹性半空间的附加应力系数;Pc为开挖土的土重;γ′为坑底土的平均有效重度,规模较大的基坑αz可以取为1。

将开挖卸除的土体重量视作附加应力,根据弹性力学中的平面应变计算公式,把土的竖向隆起变形看成一维问题,根据分层总和法可将土体回弹量S(z)与深度z之间的关系表示为:

(19)

式中,Eri为各土层的回弹模量;Hi为各土层厚度。

ψc为考虑坑底土侧向受压影响的修正系数,大面积基坑取1.0,长条形基坑取2.0[3]。

当考虑回弹深度范围内为均质土时:

(20)

式中,H为开挖深度;Es土体的回弹模量。

将式(20)代入式(17)中可得:

(21)

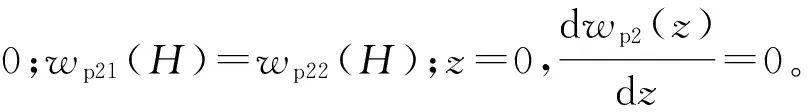
则式(21)的解可表示为:

(22)

式中,

2 桩顶荷载与分步开挖

2.1 立柱桩桩顶荷载

关于支撑对立柱桩产生的竖向荷载的计算,规范[10]提出对形状比较规则的支撑可以采取以下方法近似计算:在垂直荷载作用下,支撑的内力和变形可近似按单跨或多跨梁计算,计算跨度取相邻立柱桩的中心距,立柱桩的轴向力可以取纵、横向支撑的支座反力和。则可以计算桩顶荷载:

pp=q(l1+l2)A

(23)

式中,q支撑的重度;l1和l2为纵、横向支撑间距;A支撑的横截面面积。

2.2 分步开挖步骤

实际的基坑开挖过程采用分步开挖,采用先撑后挖的开挖流程。先浇注第一道支撑,待其强度达到设计强度后,开挖土层至第二道支撑设计深度处,此时土体带动立柱桩产生一定的隆起位移,同时支撑荷载使立柱产生下沉的趋势。继续施工第二道支撑并在满足条件后开挖第二层土,立柱桩将在原来的基础上产生新的隆起位移。依次进行,直至开挖到坑底,浇筑底板完成。各开挖工况如图4所示。

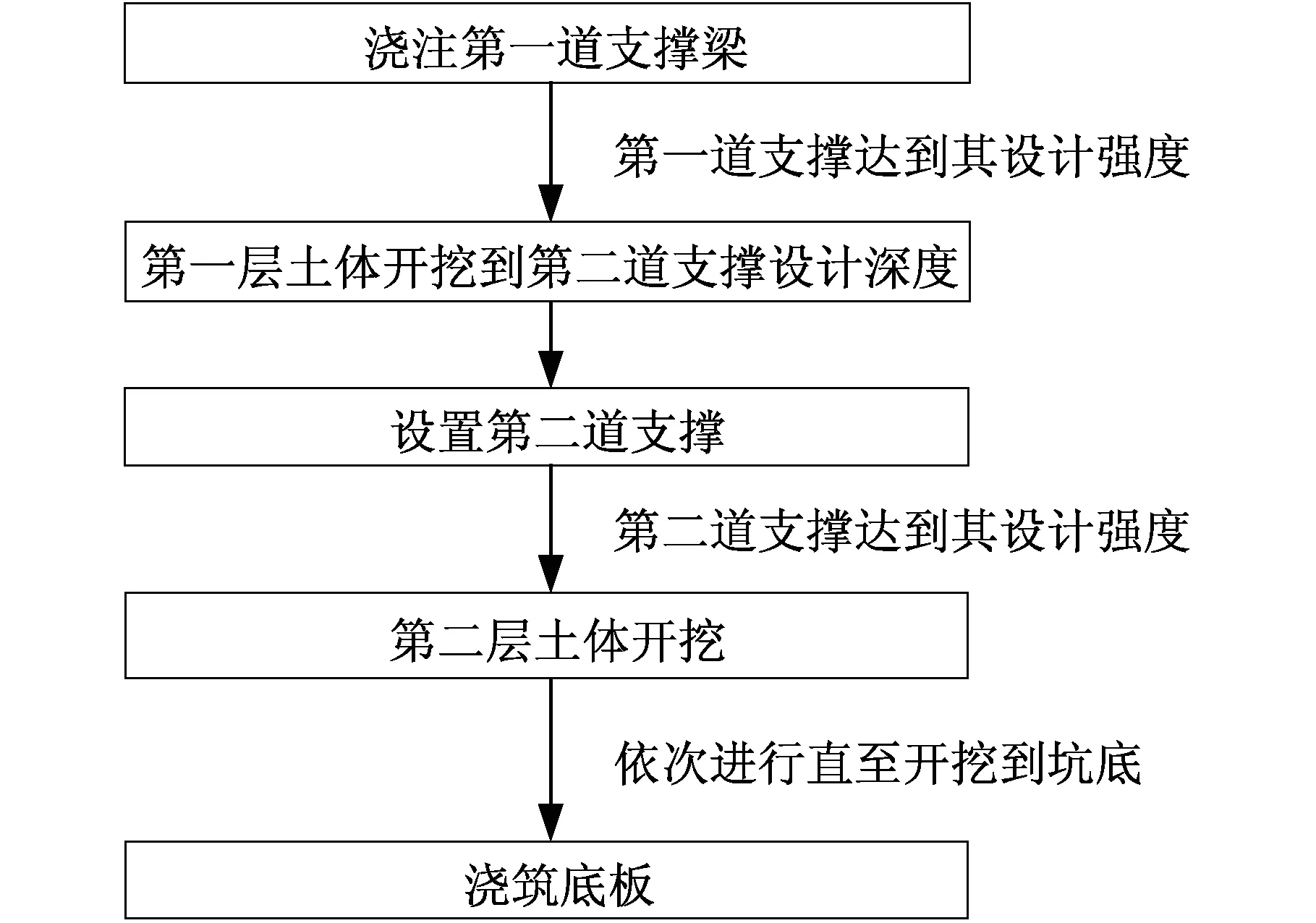
图4 基坑开挖施工流程工况图Fig.4 Working diagram of excavation process

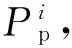
(24)

3 验证与分析

3.1 实例验证

上海黄浦区五坊园三期基坑开挖面积约12 000 m2,属于大面积基坑,因此ψc取1.0,基坑内部采用两道混凝土支撑,支撑截面800 mm×800 mm,第一道钢筋混凝土支撑中心标高为-1.700 m,第二道钢筋混凝土支撑中心标高为-6.200 m,支撑平面间距在6～10.625 m。支撑立柱采用钢格构立柱,支撑立柱截面为480 mm×480 mm,立柱桩统一设置为φ800 钻孔灌注桩,有效桩长24 m,桩身混凝土设计强度等级C35。基坑开挖深度9.6 m,采用明挖顺作法施工。

由于基坑实行全过程监测,所以能监测到每次开挖的立柱位移。本文选取立柱桩代表性测点,其所在开挖区的立柱桩及围护平面布置和支撑剖面简图如图5所示。

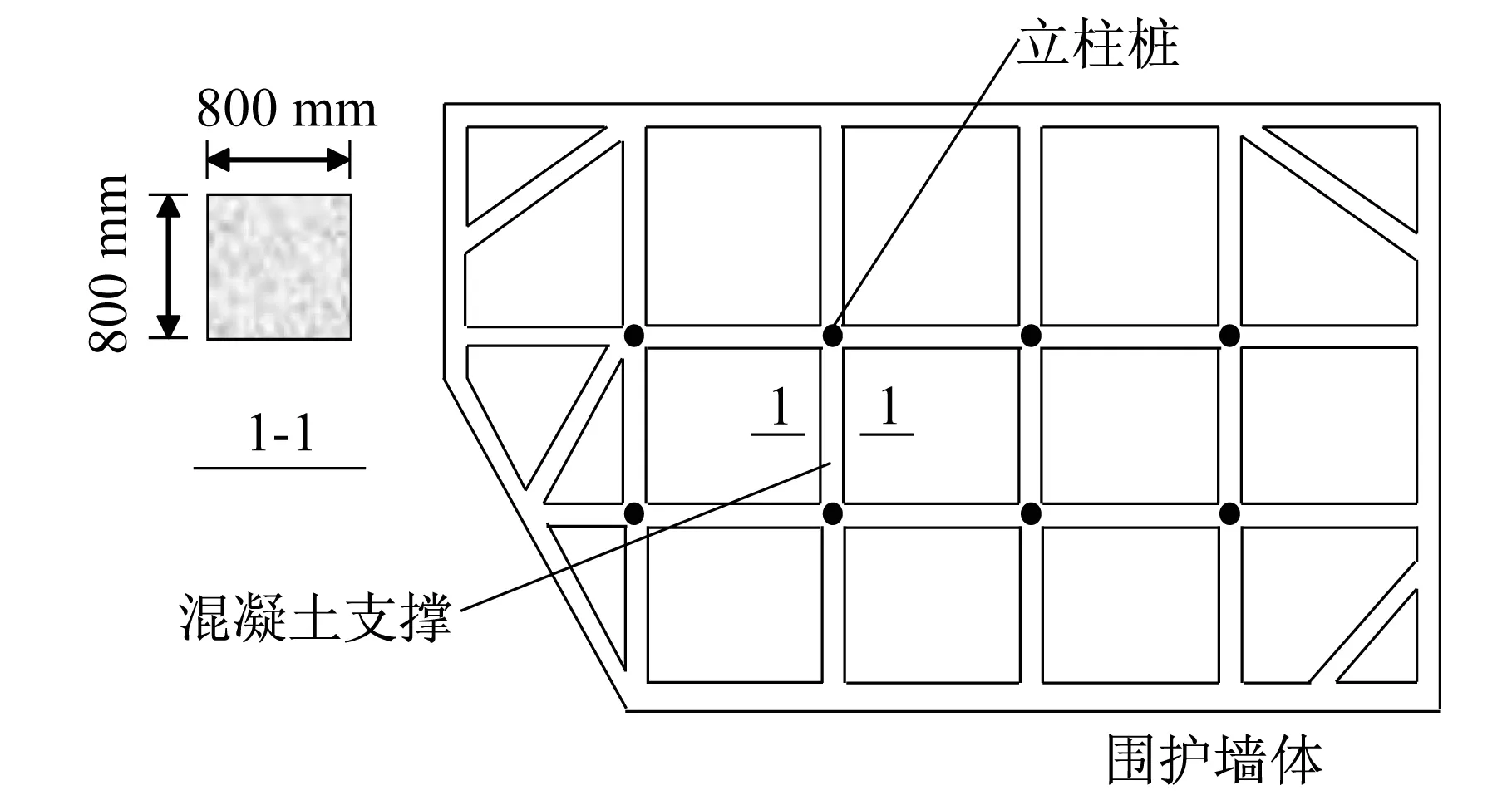
图5 围护平面和支撑剖面图Fig.5 Retaning structure plane and supporting structure profile

立柱桩直径0.8 m,桩身弹性模量为30 GPa,其中支撑间距为7 m和6 m,代入式(23)可得Pp=416 kN,考虑实际工程中支撑底部浇筑200 mm厚C20混凝土垫层兼作底模,且上方有施工栈桥,每道支撑荷载产生的竖向荷载效应取450 kN。开挖区土层参数如表1所示。本算例土层按均质土简化计算,土层参数取计算深度内的加权平均值,其饱和重度为17.5 kN/m3,回弹模量为11.3 MPa。

表1土体物理力学参数表

Table 1 Physical and mechanical parameters of soil

施工过程分为5个阶段,如表2所示。

表2施工工况一览表

Table 2 List of construction conditions

由于表层土体开挖对立柱沉降影响较小,故未检测阶段1的立柱隆沉,主要分析阶段2至阶段5立柱的隆沉变化,实测立柱桩隆起变形如图6所示。

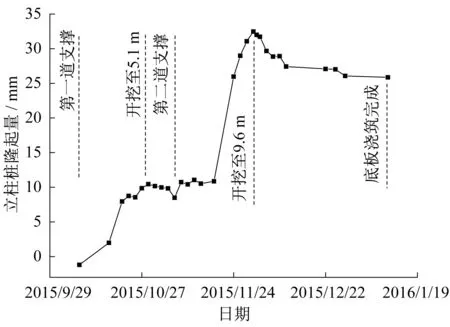
图6 立柱桩桩顶隆起位移实测图Fig.6 Measured displacement of uplift of soldier pile

由图6可见,开挖初期立柱呈现出下沉趋势,这是因为此阶段基坑开挖深度较浅,土体回弹变形不足以抵消立柱和土体自重荷载引起的沉降。随着基坑的开挖,基坑隆起量逐步增加,由于基坑隆起产生的立柱桩上浮量也逐步加大。同时,第3阶段大部分测点的隆起速度均比较慢,且变化幅度较小。阶段4浇筑第二道支撑后,立柱隆起位移略有下降,支撑作用效果明显,证明假设1成立,每一次开挖均是一次桩土重新变形协调的过程。随后第5阶段立柱隆起迅速增强,这是由于基坑开挖深度较深,开挖土方质量较大,土体大量卸荷,使得立柱回弹隆起值迅速增大,开挖至坑底时立柱桩隆起量达到最大值为33 mm。

根据上文方法编制MATLAB程序,计算得出立柱桩的位移值与实测值的对比情况如图7所示。

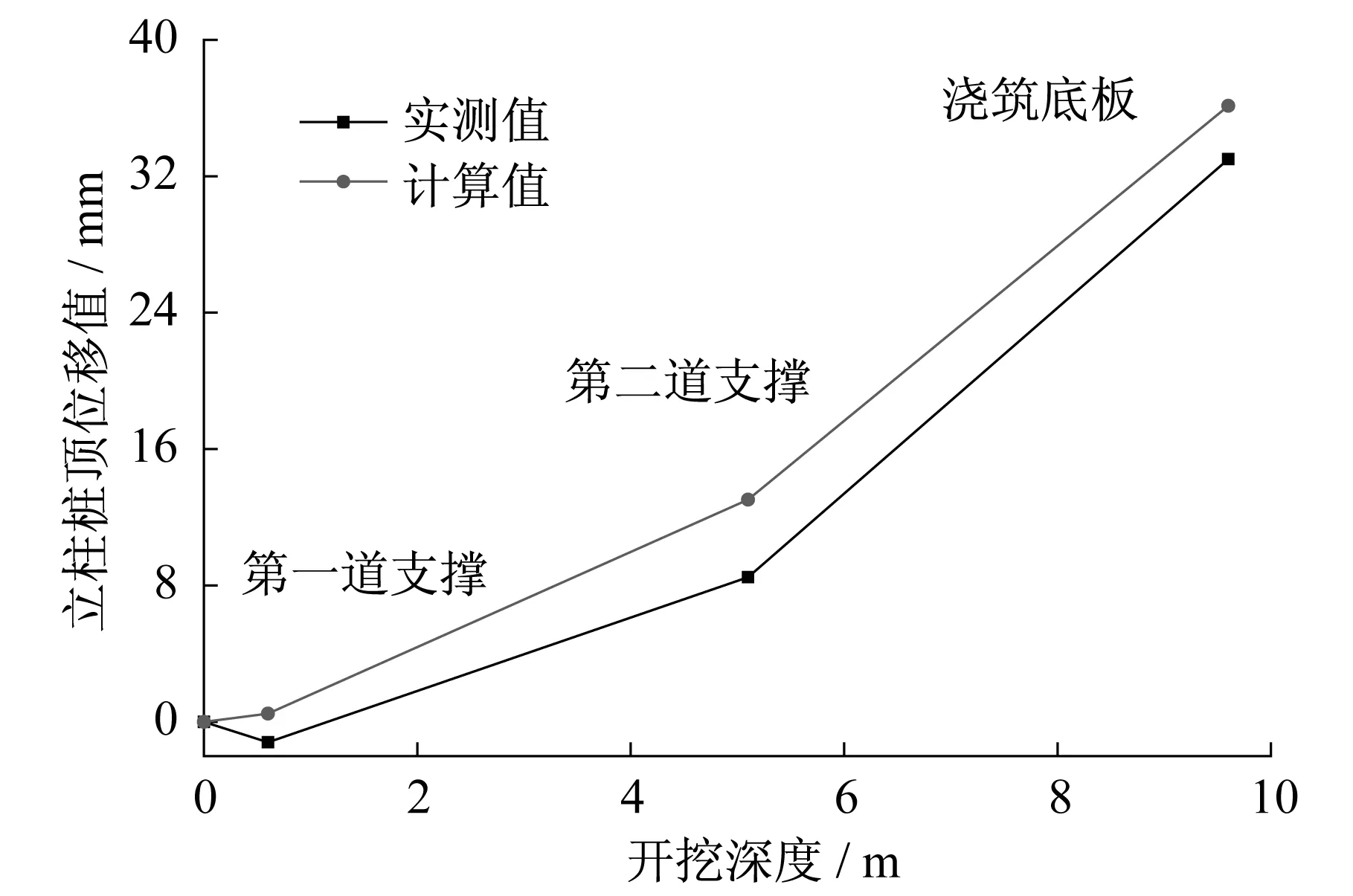
图7 实测隆起值与计算隆起值对比图Fig.7 Comparison between measured uplift value and calculated uplift value

由图7可见,本文方法可以较为合理预测立柱桩在不同开挖阶段的隆起变形。开挖至底层时计算值为36.12 mm,与实测值较为接近。从图中还可以看出,第三皮土的开挖产生的立柱隆起位移增幅大于第二皮土开挖产生的隆起位移。开挖深度越深,隆起效应越强。支撑对立柱变形有一定约束作用,但土体开挖卸荷回弹引起的隆起位移效果明显大于支撑的约束作用,由此可见立柱隆起位移大部分是土体卸荷回弹引起。计算值大于实测值,这是由于上述计算未考虑桩体自重荷载和围檩、围护墙使得支撑向立柱产生向下的位移趋势,使得计算值偏大。但是土体卸荷回弹后对桩产生向上的负摩阻力,桩身拉长位移未计算,使得计算值偏小。两者在一定程度上相互抵消,使得本案例立柱桩在隆起位移计算值与实测值吻合较好,可有效保证结构的设计安全。

3.2 算例分析

假定某一基坑开挖深度H=16 m,基坑每步开挖4 m设置一道支撑,开挖土体重度γ=18 kN/m3,坑底土为均质土,土体回弹模量Es=12 MPa,泊松比μ=0.4,土体静止侧压力系数K0=0.4。桩的弹性模量E=30 GPa,桩径D=0.8 m,桩长L=30 m,每道支撑荷载产生的竖向荷载效应取参考实际工程近似取值每道450 kN。为简化计算方法,与通常的压缩变形计算中仅考虑压缩模量的方法类似,本文的立柱桩隆起量计算也仅采用土体回弹模量计算,其近似性在工程合理范围。

图8为不同土体回弹模量对应的立柱桩位移情况。可以看出,土体回弹模量的大小对立柱桩隆起位移影响明显。在开挖深度一定的情况下,立柱桩隆起量随着桩侧土体的回弹模量的增大而减小。软土地区土体回弹模量小,卸荷引起的立柱隆起量大,严重时可能导致支撑结构体系失稳。

图9为不同开挖步长对应的立柱桩位移规律。由图可见,当开挖步长3.2 m时(5道支撑),虽然立柱桩隆起位移较小,但支撑道数较多,施工工序增多并造成工程浪费。开挖步长5.3 m时(3道支撑),立柱桩隆起位移较大,易导致支撑体系的失稳破坏。而步长4 m (4道支撑)和步长4.5 m (4道支撑)对应立柱桩隆起量值接近。因此合理设计分步开挖步长和支撑间距能有效保证结构稳定并节约工程费用。

4 结 论

(1) 本文分析了土体回弹和支撑体系产生的竖向荷载效应对立柱桩隆沉的影响,并给出了立柱桩隆起量的计算方法。该方法考虑了土层特性、基坑分步开挖和支撑体系的作用,分析了土体回弹和立柱桩隆沉之间的相关性。

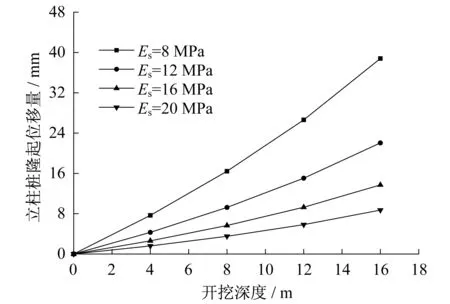
图8 不同桩侧土体回弹模量对应的立柱桩桩顶隆起位移图Fig.8 Displacement diagram of top uplift of soldier pile with different soil resilience modulus

图9 不同开挖步长对应的立柱桩桩顶隆起位移对比图Fig.9 Displacement of top uplift of soldier pile corresponding to different excavation steps

(2) 本文提出的方法所用土层物理和力学参数均较容易取得,实例分析表明本文方法可以较好预估不同开挖工况下立柱桩的隆起位移。

(3) 开挖卸荷坑底土回弹对立柱桩隆起变形产生决定性作用,土体回弹模量的大小对立柱桩隆起位移影响明显。

(4) 软土地层复杂环境下不同基坑开挖方式对立柱桩隆起位移影响较大,基坑支撑的设置和浇筑对立柱桩的竖向位移有很好的限制作用。因此在实际工程中应优化施工方案,合理设计支撑和围护结构。

[1] 陈明,李镜培.开挖过程对桩基影响的工程实例对比分析[J].同济大学学报(自然科学版),2014,42(5):677-682.

Chen Ming,Li Jingpei.Metro project-based analysis of excavation impact on pile bearing capacity[J].Journal of Tongji University(Natural Science),2014,42(5):677-682.(in Chinese)

[2] Poulos H G,Davis E H.Pile foundation analysis and design[M].New York:Wiley,1980.

[3] 楼晓明,杨晶,李德宁,等.立柱桩在深基坑分步开挖过程中的上拔位移分析[J].岩土工程学报,2013,(1):193-198.

Lou Xiaoming,Yang Jing,Li Dening,et al.Uplift displacement of soldier piles during stepped excavation of deep foundation pits[J].Chinese Journal of Geotechnical Engineering,2013,(1):193-198.(in Chinese)

[4] 贺翀.深基坑的立柱桩隆起计算[J].岩土工程学报,2010,(S1):74-78.

He Chong.Calculation of heave of soldier piles in deep foundation pits[J].Chinese Journal of Geotechnical Engineering,2010,32(S1):74-78.(in Chinese)

[5] 巢斯,王磊,雷小虎,等.上海软土地区深基坑回弹引起桩拉力的探讨[J].结构工程师,2009,(05):88-92.

Chao Si,Wang Lei,Lei Xiaohu,et al.Discussion on tensile force of piles caused by subsoil rebound in soft soil area[J].Structural Engineers,2009,25(5):88-92.(in Chinese)

[6] 范巍.大面积深基坑开挖过程中桩基受力特性研究[D].上海:上海交通大学,2007.

Fan Wei.Behavior of pile foundation during large-scale deep excavation[D].Shanghai:Shanghai Jiao Tong University,2007.(in Chinese)

[7] 肖健.考虑工程桩存在的深基坑回弹空间效应有限元分析[D].天津:天津大学,2004.

Xiao Jian.FEM analysis on 3D behavior of the pit resilience considering foundation piles[D].Tianjin:Tianjin University,2004.(in Chinese)

[8] 肖宏彬,钟辉虹,王永和.多层地基中桩的荷载传递分析[J].中南工业大学学报(自然科学版),2003,(06):687-690.

Xiao Hongbin,Zhong Huihong,Wang Yonghe.Analysis of pile’s load transfer in layered soils[J].Journal of Central South University of Technology (Natural Science),2003,(06):687-690.(in Chinese)

[9] 肖宏彬.竖向荷载作用下大直径桩的荷载传递理论及应用研究[D].长沙:中南大学,2005.

Xiao Hongbin.Theoretical and application research on load transfer of vertically loading large diameter piles[D].Changsha:Central South University,2005.(in Chinese)

[10] DGTJ08-61—2010 上海市基坑工程技术规范[S].2010.

DGTJ08-61—2010 Technical code for excavation engineering[S].2010.(in Chinese)