核电厂钢筋混凝土构筑物氯离子侵蚀评估

汤志杰 廖开星 李 毅 孔祥龙 遆文新

(苏州热工研究院有限公司寿命中心,苏州 215004)

0 引 言

Mehta教授[1]曾在《混凝土耐久性——五十年进展》主旨报告中指出:“当今世界混凝土破坏原因,按重要性递减顺序排列是:钢筋腐蚀、冻害、物理化学作用。”而在引起钢筋锈蚀的因素之中,氯离子侵蚀作用最为显著。由于国内大部分核电站处于高温高湿的滨海地区,海风和雾气中含有的氯离子极易沉积在构筑物钢筋混凝土表面,并向其内部渗透,引起钢筋的锈蚀,极大地危害了构筑物的可靠性能和安全性能。国内外许多专家和学者对基于氯离子渗透的钢筋混凝土寿命预测模型进行了大量的研究,但提出的模型大都为确定型[2],即求解时只要对其中的每个参数输入一个数值,如平均值,即能求出具体的寿命值。但在氯离子侵蚀过程中,涉及许多材料与环境变量,这些因素都是随机性的变量。因此,用概率的思想,用更成熟的可靠性理论来研究混凝土结构的氯离子侵蚀问题是更为合理的。

本文通过对某核电站安全相关构筑物现场检测获取的数据,结合模拟试验获得的参数,建立了核电厂安全相关构筑物的寿命预测模型,并采用Monte-Carlo模拟,对氯离子侵蚀进行了评估。

1 钢筋混凝土氯离子侵蚀确定型模型

氯离子在钢筋混凝土中的扩散符合Fick’s第二扩散定律[3],其表达式为

(1)

初始条件可以表示为

C(x,0)=C,x>0

(2)

边界条件可以表示为

C(0,t)=CS,t>0

(3)

C(∞,t)=C0,t>0

(4)

由于混凝土内部不断发生水化反应,氯离子扩散系数也会随时间逐渐变小,因此氯离子扩散模型也应考虑时间因素,且同时引入环境系数K,该值主要与环境温湿度有关,满足下列关系式:

(5)

D=KDt

(6)

由式(1)-式(6)得出修正后的Fick’s第二扩散定律的解析解为

(7)

式(7)中,如果氯离子的临界浓度为Ccr,混凝土保护层厚度为d,则可以推出氯离子侵蚀寿命预测公式为

(8)

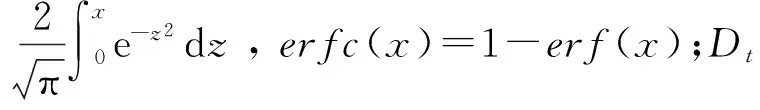
2 钢筋混凝土氯离子随机概率模型

考虑到氯离子侵蚀诱发的结构耐久性失效的关键点是钢筋开始锈蚀,本文就将其作为耐久性失效的主要模式。这样,结构“失效”的状态可以定义为在混凝土保护层厚度处,氯离子浓度达到引起钢筋锈蚀的临界氯离子浓度Ccr,因此抵抗“破坏”的抗力R可以定义为钢筋混凝土保护层厚度d,而环境荷载S定义为混凝土中氯离子的侵蚀深度dc。则氯离子侵蚀环境正常使用耐久极限状态方程可写为

Z=R-S=d-dc

(9)

(10)

则失效概率Pf为

Pf=P(Z=R-S≤0)=

(11)

用失效概率Pf度量结构的可靠性具有明显的物理意义,但这种方法最主要的缺点就是,当变量较多时,需要计算多维积分,比较困难,因而可以采纳由Siemes和Rostam[4]提出的可靠性指标β来代替Pf度量结构的可靠性。可靠性指标β可按下式定义:

(12)

μz=μR-μS

(13)

(14)

式中,P目标为由可靠性指标β所决定的目标失效概率,Pf达到P目标即可判定结构失效;μz为结构函数Z的均值;σz为结构函数Z的标准差;μR为抗力R的均值;σR为抗力R的标准差;μs为环境载荷S的均值;σs为环境载荷S的标准差。

由于钢筋混凝土保护层厚度d和氯离子扩散系数D0是影响钢筋锈蚀的最重要参数,对混凝土结构的耐久性极大,因此本文假定这两个参数为随机量,其他参数根据实际情况取为定值。从而随机变量dc的均值μdc和标准差σdc可由下式表示:

(15)

(16)

β值可由下式表示:

(17)

3 工程实例计算

3.1 模型参数的概率分布特征及取值

处于滨海大气环境下的某核电站安全相关构筑物,其混凝土强度等级为C50,表面无涂层保护,已服役20余年。经现场检测,对其钢筋混凝土保护层厚度d进行统计分析,见图1,经K-S检验不否定其服从正态分布假设,其分布特征为N(58,92),mm。同时对该构筑物迎风面墙体取混凝土粉末,测得平均水溶性表面氯离子浓度Cs的值为0.144%(占胶凝材料的质量百分比),根据ACI-318《混凝土结构设计规范》[5]的规定,对于预应力钢筋混凝土,其临界水溶性氯离子浓度Ccr应取0.06%(占胶凝材料的质量百分比)。

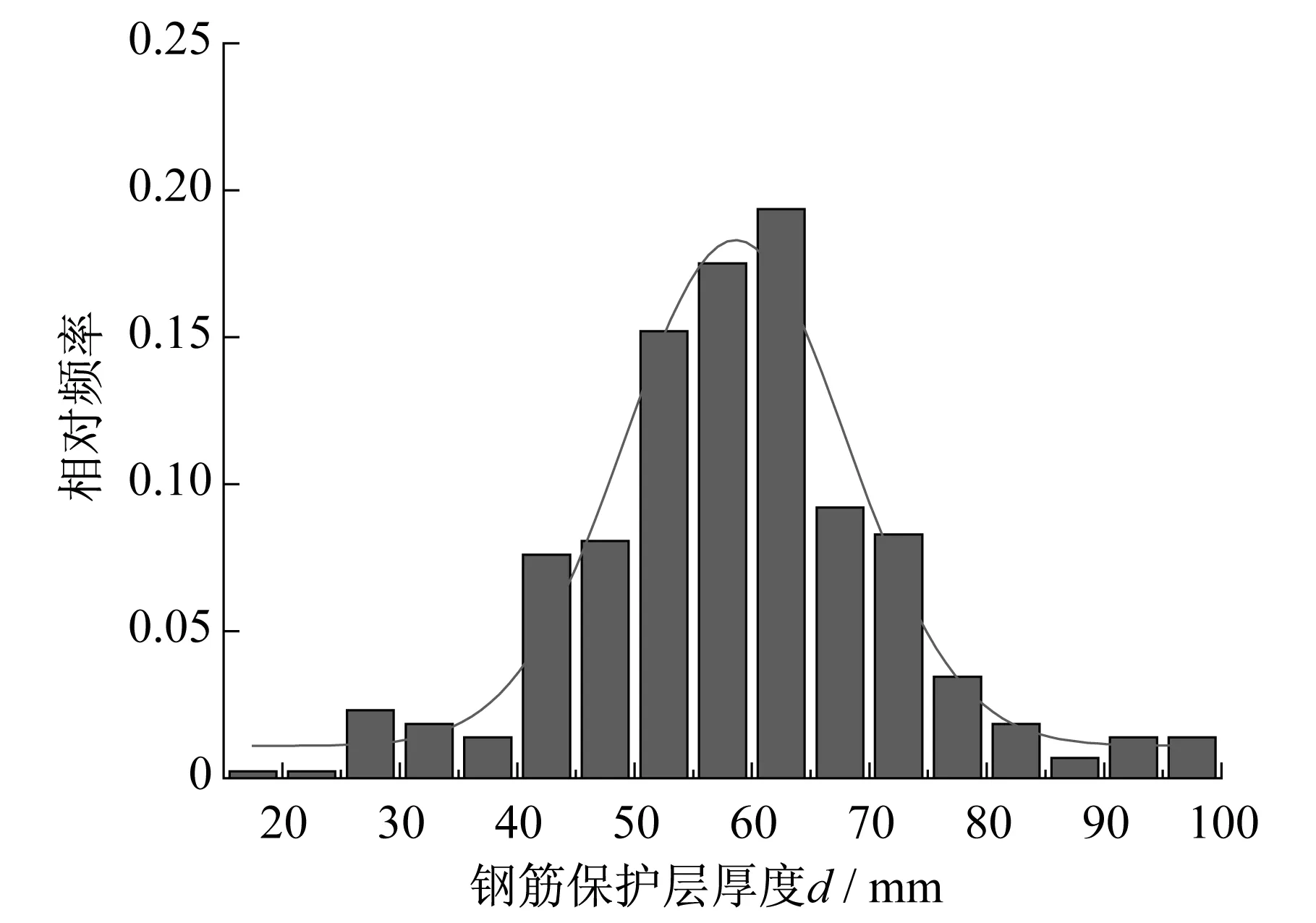
图1 钢筋保护层厚度频率直方图Fig.1 Relative frequency of cover

另外,对该安全相关构筑物的模拟混凝土分别进行了RCM测试和盐雾试验[6],获得临期为28 d的氯离子扩散系数D0的分布特征为N(162.91,32.582)×10-12m2/s和扩散系数衰减指数m为0.56。结合该电站的实际环境,环境系数K为0.448。具体相关影响参数取值见表1。

表1模型参数的概率分布特征及取值

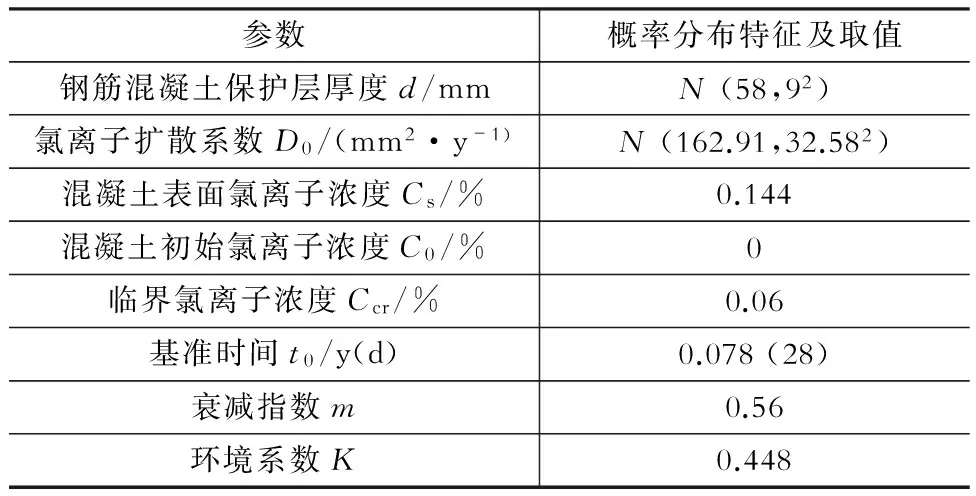
Table 1 The value of model parameters

3.2 构筑物耐久性寿命的概率分布特征

利用表1中参数代入式(8)中进行Monte-Carlo模拟(模拟次数为50 000次),获得氯离子侵蚀条件下构筑物耐久性寿命T的分布特征(图2)。从中可以看出结构耐久性寿命呈现偏态分布特征,初锈时间峰值点T为6 700年左右。

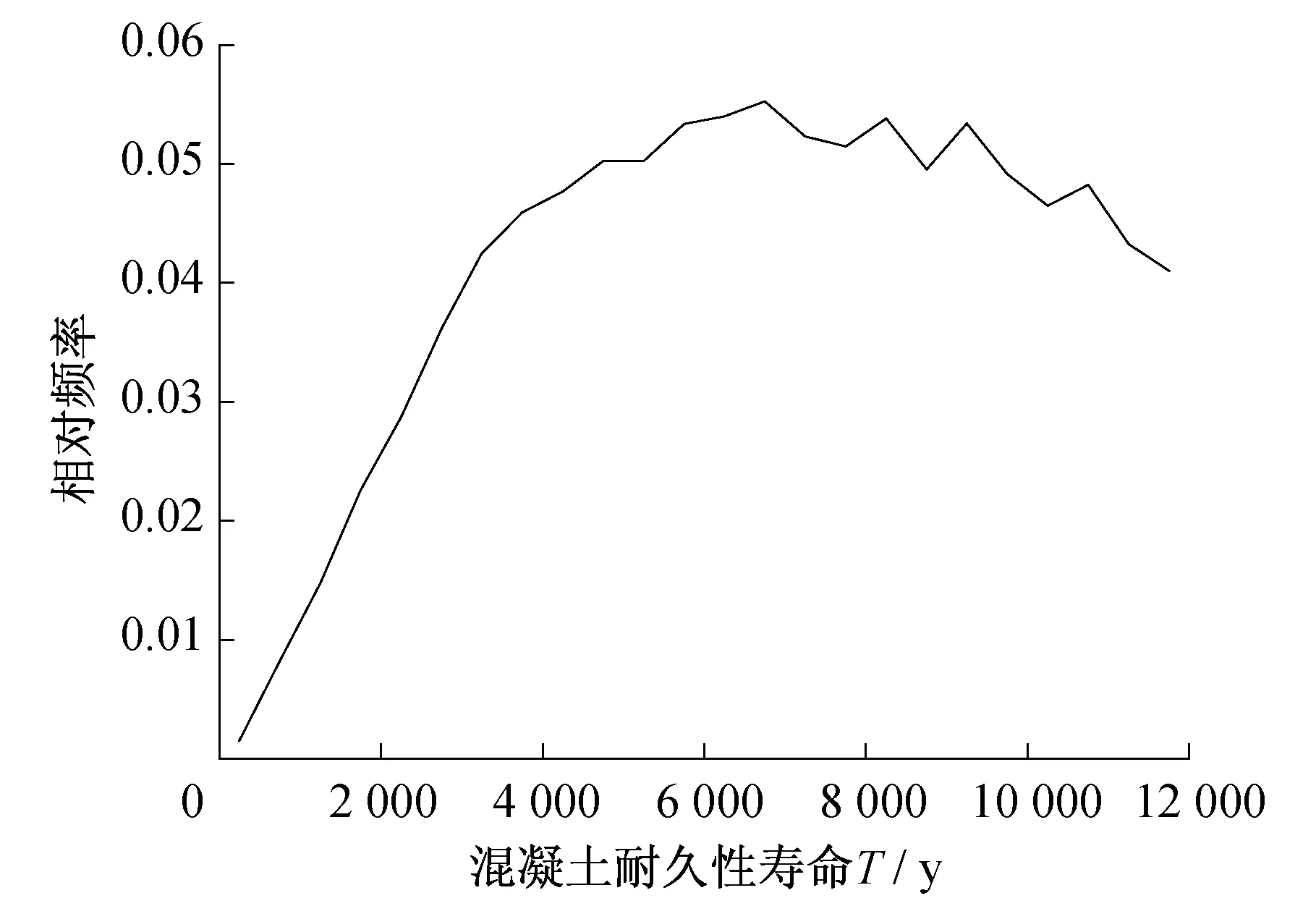
图2 结构耐久性寿命的频率直方图Fig.2 Relative frequency of life of concrete structure

3.3 构筑物氯离子侵蚀耐久性寿命预测

同样利用表1中参数代入式(11)进行Monte-Carlo模拟(模拟次数为50 000次),得到结构服役失效概率与服役时间的曲线图,如图3所示。从图3中可以看出,失效概率为Pf随着服役时间的增长而增大。在钢筋混凝土耐久性设计中,一般钢筋锈蚀概率控制在5%～10%是比较符合工程的实际情况[7-8]。核电站安全相关构筑物一般设计寿命为60年以上,从图中可以看出,服役时间为100年时,其失效概率Pf仅为2×10-3%。因此该电站安全相关构筑物能够确保安全服役100年以上。

氯离子侵蚀耐久性极限状态的设置标准见表2。对于氯离子侵蚀导致的钢筋开始锈蚀或者锈蚀导致的保护层开裂的状态而言,从正常使用耐久性能的失效到结构完全破坏(承载力失效)的时间较长,而荷载作用的周期也较长,因而可以将其所对应的β值取得较小,失效概率Pf取得高些[9]。依据耐久性极限状态的设置标准以及一些调查结果,本文将β值取为1.645,作为规定的耐久性极限最小可靠度指标。

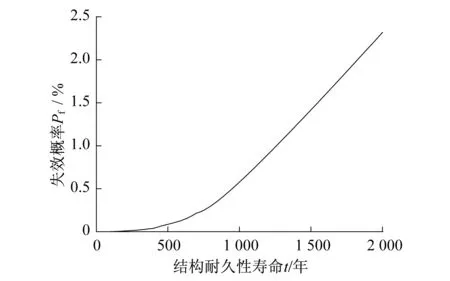
图3 失效概率与结构服役时间关系Fig.3 The relationship of Pf and service time

表2氯离子侵蚀耐久性极限状态的设置标准

Table 2 Standard of durability limit state of chloride ingress

采用式(17)可以计算可靠度指标与服役时间的关系,其曲线图如图4所示。从图4中可以看出,当可靠度指标β取为1.645时,t为2 840年。

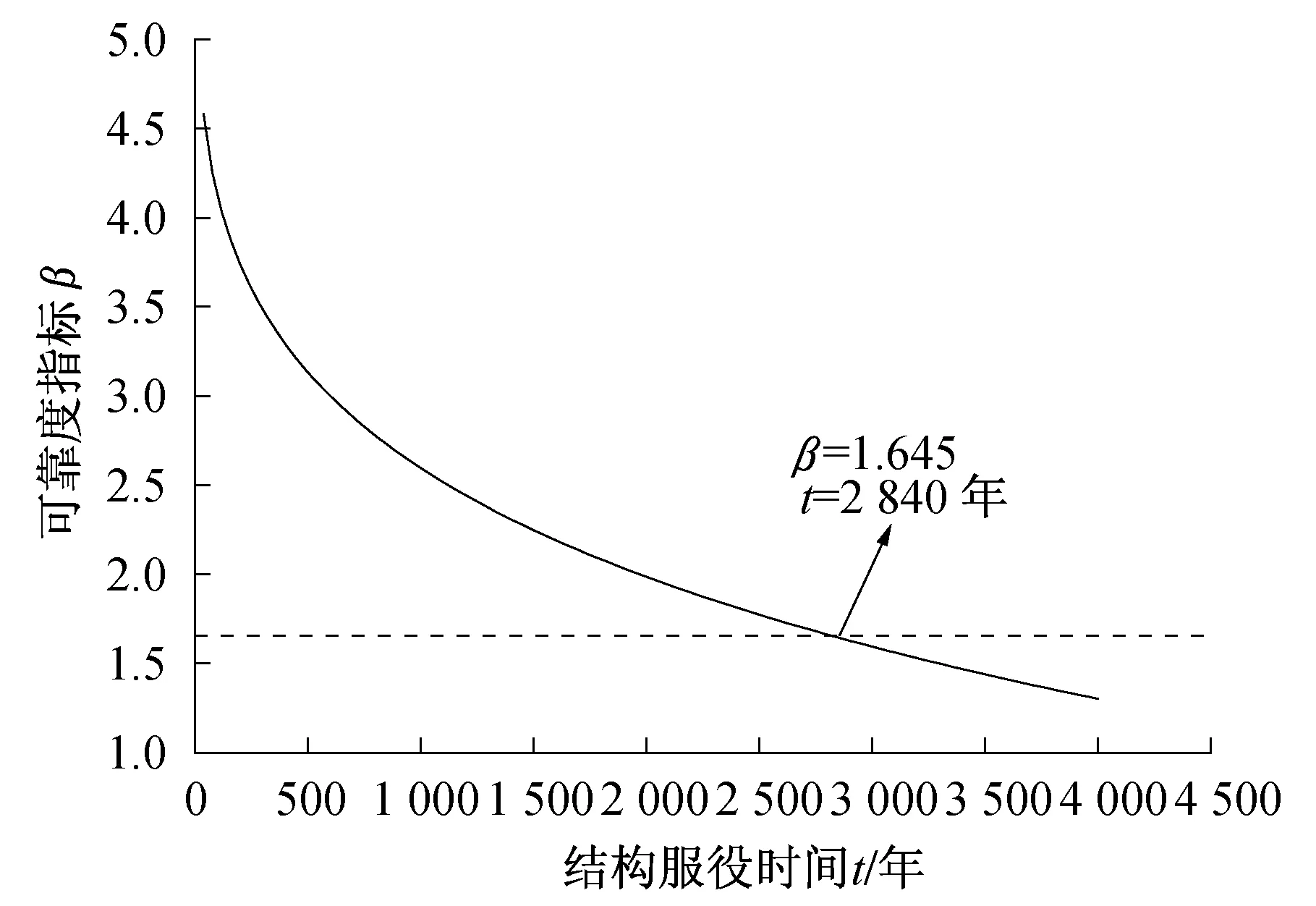
图4 可靠度指标与结构服役时间关系Fig.4 The relationship of β and service time

4 结 语

本文考虑了时间及环境因素,修正了Fick’s第二定律的误差函数解,并以此建立钢筋混凝土氯离子侵蚀随机概率寿命预测模型;通过Monte-Carlo模拟发现氯离子侵蚀条件下某核电站安全相关构筑物在服役100年后的失效概率Pf仅为2×10-3%,当可靠度指标β取为1.645时,t为2 840年,因此该核电站安全相关构筑物能够确保安全服役100年以上。实际上,影响氯离子侵蚀的因素还很多,因此在使用本文模型时还需依据大量实验数据和相关参数现场检测结果进行取值,这样才能使预测结果更好地服务于实际工程。

[1] 洪定海.混凝土中钢筋的腐蚀与保护[M].北京:中国铁道出版社,1998.

Hong Dinghai.Corrosion and protection of reinforcement in concrete [M].Beijing:China Railway Publishing House,1998.(in Chinese)

[2] 练继建,张杰,吴慕丹,等.海洋环境要素综合影响下混凝土中氯离子的传输模型[J].天津大学学报(自然科学与工程技术版),2016,49(4):333-340.

Lian Jijian,Zhang Jie,Wu Mudan,et al.Chloride ion transport model in concrete under combined influence of marine environment factors[J].Journal of Tianjin University (Science and Technology),2016,49(4):333-340.(in Chinese)

[3] 彭建新,夏伟.预应力混凝土中氯离子扩散模型分析[J].交通科学与工程,2015,31(3):73-77.

Peng Jianxin,Xia Wei.Diffusion model of chloride ion in prestressed concrete[J].Journal of transport science and engineering,2015,31(3):73-77.(in Chinese)

[4] 岳著文,李镜培,杨博.考虑对流条件下氯离子在混凝土中的输运计算[J].同济大学学报(自然科学版),2015,43(1):60-66.

Yue Zhuwen,Li Jingpei,Yang Bo.Calculation of chloride ions transportation in concrete considering convection[J].Journal of Tongji University (Natural Science),2015,43(1):60-66.(in Chinese)

[5] 高远,陆春华,袁思奇,等.海工混凝土氯离子分布概率模型分析与应用[J].水利水运工程学报,2016(1):37-43.

Gao Yuan,Lu Chunhua,Yuan Siqi,et al.Application analysis of probability model for chloride ion erosion distribution in marine concrete structure[J].Hydro-Science and Engineering,2016( 1) :37-43.(in Chinese)

[6] 彭建新,王华.氯盐侵蚀下钢筋混凝土氯离子扩散系数试验及其概率分析[J].中国公路学报,2014,27(6):77-81.

Peng Jianxin,Wang Hua.Experimental study on chloride ion diffusion coefficient in concrete and probabilistic analysis of its influence on deterioration performance of RC structures[J].China Journal of Highway and Transport,2014,27(6):77-81.(in Chinese)

[7] Collepardi M,Marcialis A,Turrizzani R.The kinetics of penetration of chloride ions into the concrete[J].Cem and Concr Res,1970 (4):157-164.

[8] Tang L,Gulikers J.On the mathematics of time-dependent apparent chloride diffusion coefficient in concrete[J].Cem Concr Res,2007,37:589.

[9] 余红发,孙伟.混凝土在多重因素作用下的氯离子扩散方程[J].建筑材料学报,2002,3(5):240-246.

Yu Hongfa,Sun Wei.Diffusion equations of chloride ion in concrete under the combined action of durability factors[J].Journal Of Building Materials,2002,3(5):240-246.(in Chinese)

[10] 赵国藩.工程结构可靠性理论与应用[M].大连:大连理工大学出版社,1996.

Zhao Guofan.Engineering structure reliability theory and application[M].Dalian:Dalian University of Technology Press,1996.(in Chinese)

[11] Siemes A J M,Rostam S.Durable safety and serviceability-A performance based design format[R].IABSE Report 74:Proceedings IABSE Colloquium ‘Basis of Design and Actions on Structures-Background and Application of Eurocode 1,Delft,1996.

[12] 元成方,牛荻涛.基于可靠度理论的海工混凝土结构寿命预测[J].武汉理工大学学报,2013,35(4):73-78.

Yuan Chengfang,Niu Ditao.Life prediction of the marine concrete structure based on the reliability theory[J].Journal of Wuhan University of Technology,2013,35(4):73-78.(in Chinese)

[13] Building Code requirements for structural concrete (ACI 318M-11) and commentary[S].American Concrete Institute,USA,2011.

[14] 刘志勇,孙伟,周新刚.基于Monte Carlo随机计算的海工混凝土使用寿命预测[J].东南大学学报(自然科学版),2006,36(增刊II):221-225.

Liu Zhiyong,Sun Wei,Zhou Xingang.Service life prediction of marine concrete based on Monte Carlo stochastic calculation[J].Journal of Southeast University (Natural Science Edition),2006,36(Sup II):221-225.(in Chinese)

[15] 张建强.混凝土氯离子侵蚀的概率分析[J].结构工程师,2009,25(4):48-52.

Zhang Jianqiang.Probabilistic analysis for chloride penetration inside concrete[J].Structural Engineers,2009,25(4):48-52.(in Chinese)

[16] 汤志杰,廖开星.滨海环境安全壳混凝土氯离子侵蚀规律研究[J].混凝土,2015(5):66-69.

Tang Zhijie,Liao Kaixing.Diffusion of chloride ion into containment concrete under coastal environment[J].Concrete,2015(5):66-69.(in Chinese)

[17] 刘秉京.混凝土结构耐久性设计[M].北京:人民交通出版社,2007.

Liu Binjing.Durability design of concrete structure[M].Beijing:China Communications Press,2007.(in Chinese)

[18] 中国土木工程学会.CCES 01—2004 混凝土结构耐久性设计与施工指南[S].2004.

China Civil Engineering Society.CCES 01—2004 Guide to durability design and construction of concrete structures[S].China’s Academy of Civil Engineering,2004.(in Chinese)

[19] 马亚丽.基于可靠性分析的钢筋混凝土结构耐久寿命预测[D].北京:北京工业大学,2006.

Ma Yali.Reliability based durable life prediction of reinforced concrete structures[D].Beijing:Beijing University of Technology,2006.(in Chinese)