摩托车前后悬架振动模型参数测试
冷传刚
(天津大学内燃机研究所 天津 300072)
引言
摩托车悬架装置,对摩托车的乘坐舒适性和行驶平稳性有着重要的影响,如果悬架装置设计不合理,会对舒适性产生极大影响[1]。而解决乘骑时整车共振,频率过高等摩托车高速行驶时的不稳定问题,前提就是要建立摩托车前后悬架振动系统的振动模型,并确定轴荷、刚度和阻尼系数等振动参数。振动模型参数是否合理,是影响乘坐舒适性的关键。轴荷可以通过测量直接得到,而刚度和阻尼系数参数却很难直接得到,比较简便的方法就是先确定悬架系统的偏频和阻尼,进而通过振动理论计算得到。偏频和阻尼是结构动力学的一个重要概念,偏频指车辆质量系统中,某一个质量振动时的部分频率。阻尼系数就是使自由振动衰减的各种摩擦和其它阻碍作用。本文通过实验方法测得了某大排量摩托车的轴荷、偏频和阻尼,并通过理论计算得到了摩托车悬架系统的各个振动模型参数。
1 测试原理
摩托车前后悬架减震器的振动模型如图1所示,该模型为一个双自由度的振动系统,其中m1,m2分别为双自由度的质量,k1,k2为双自由度的刚度,c1,c2为双自由度的阻尼。

图1 摩托车悬架振动模型
根据振动学理论,系统前后部分的固有频率分别为:

进行偏频和阻尼比的测试时,通常测量摩托车减震器上方的振动加速度,其加速度具有如下形式:

可以看出,系统做有阻尼的自由振动时,其位移和加速度的固有频率是相同的,可以通过测量加速度的固有频率确定位移的固有频率。加速度的振幅随时间逐渐衰减,图2为加速度理论衰减曲线。

图2 加速度理论衰减曲线
如果相邻两峰间的时间间隔为T,则偏频f为:

式中:T为悬架振动周期(s),阻尼比ξ为[3]:

在进行阻尼比的计算时,由于存在零线偏移,很难确定准确的峰值,故对公式(6)进行修正,将多个峰值的结果进行综合计算,修正公式如公式(7)所示。

通过以上分析可以看出,只要得到前后悬架的加速度自由衰减振动曲线,即可确定车辆的偏频和阻尼比。
2 测试流程
偏频和阻尼比的测试过程如图3所示。本次测试采用滚下法[4]使车辆悬挂系统产生自由衰减振动。测试前,将非测试端的减震器用锁紧装置锁住,如图4所示。加速度传感器置于减震器上方,将车辆测试端的车轮,沿斜坡驶上凸块,本次测试使用的凸块高度为158 mm,测试时样车挡位处于空挡,发动机处于熄火状态,将样车车轮从凸块上推下,车轮滚下时尽量保证轮胎轴线与地面平行,滚下瞬间人不扶车辆确保车辆不受任何外力。用LMS数据采集软件记录车身上自由衰减振动的时间历程,每次记录时间不小于6 s,保证衰减振动曲线完整,共记录3~5次。前后轴荷的测量通过数字指示称直接称量,保存实验结果。

图3 偏频阻尼比测试

图4 锁紧装置锁住减震器
前后轴荷的测量通过数字指示称直接称取,如图5、图6所示,记录实验结果。

图5 轴荷测试过程

图6 轴荷测试结果
3 实验结果分析
图7为采集到的某大排量摩托车前减震自由衰减过程原始数据,从图中可以看出,由于存在高频波的干扰,图中的曲线为各个频率波形的叠加,由于高频波的振动加速度信号起主导作用,从图中很难看出减震器做自由衰减振动的周期性波形,所以还需对数据进行后处理。对车身部分的振动信号进行适当频率的滤波处理,滤波后的波形如图8所示,周期性已经非常明显,读取一个或多个振动周期的时间,可以计算出前后减震器的偏频。

图7 前减震原始数据

图9 后减震初次滤波
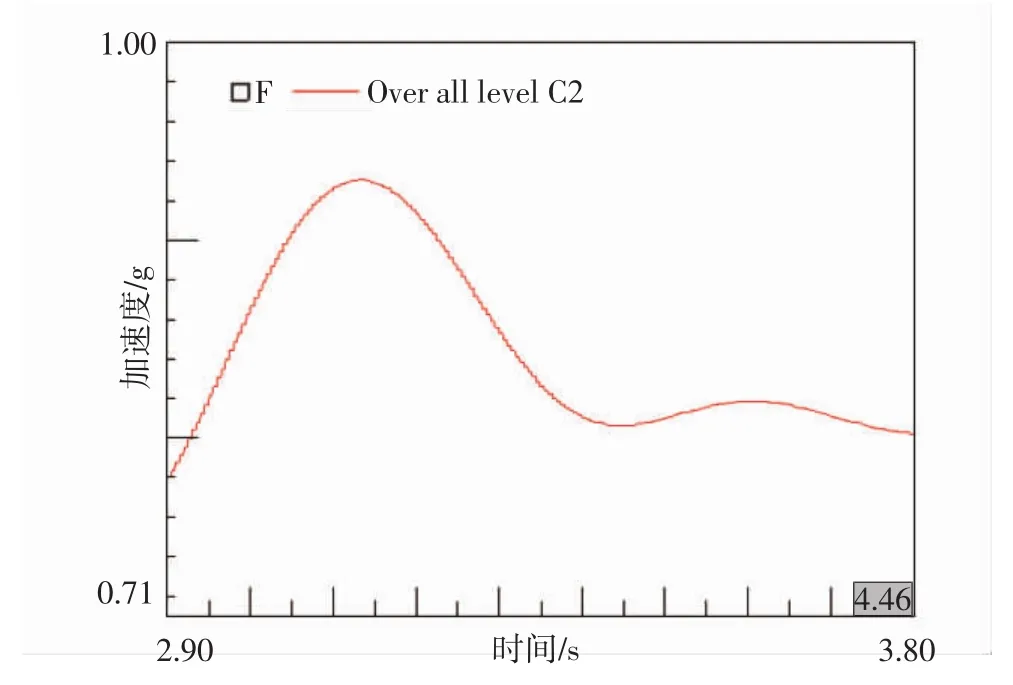
图10 后减震二次滤波
后减震器部分的衰减曲线经初次低通滤波后仍存在高频波的干扰,如图9所示,根据曲线的周期,可以粗略估计其频率为2 Hz左右,在保证不丢失悬架振动数据的前提下进行进一步的低通滤波,得到了周期性明显的衰减曲线,如图10所示,从而得到车身后部的偏频和阻尼比,结果如表1所示。

表1 偏频阻尼比结果
根据轴荷及偏频和阻尼比的测试计算结果,可以进一步求出前后悬架减震器的刚度和等效线性阻尼系数。

将各个参数带入上述公式,可以得到图1中前后悬架减震器的振动模型参数,计算结果汇总如表2所示。
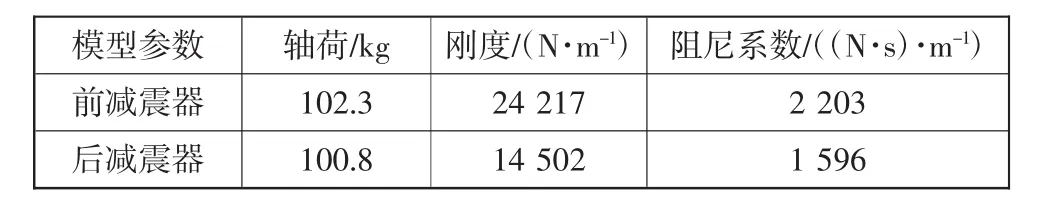
表2 前后减震器振动模型参数
4 实验结果验证
由于偏频的测试影响因素较多,而且刚度和阻尼系数结果都是由偏频结果计算得到的,为确保测试结果的有效性,用简单方法对偏频结果进行了验证。人为按压前后减震器,使摩托车前后减震器按照其固有频率振动,按压时不能破坏减震器固有频率,如图11所示。记录在一定时间内前后减震器的振动次数。

图11 偏频结果验证
5 结论
实验结果表明:两种不同方法测试结果相差在10%以内,试验结果是有效的。
1 沈好民.摩托车悬架装置结构参数分析及设计[J].摩托车技术,2012(5):38-41
2 宋康,陈潇凯,林逸.动力总成悬置系统对汽车动力学性能的影响[J].汽车工程,2016,38(4):488-494,505
3 张令弥.振动测试与动态分析[M].北京:航空工业出版社,1992
4 何璇.轮胎/车轮均匀性及相关汽车振动分析研究[D].合肥:合肥工业大学,2015

