基于DEM模拟液固流化床粒度级配对颗粒流动特性的影响

丁冬峰，程 可，陆晓峰，朱晓磊，朱凌雪

（1.南京工业大学机械与动力工程学院，江苏南京 211816；2.金陵科技学院，江苏南京 211816）

液固流化床具有混合均匀、传热和传质性能好等优点，目前已被广泛应用于化工、食品技术、湿法冶金和水处理等诸多领域[1-2]。目前对于气固流化床已经有了较为深入和系统的研究，而对液固流化床的研究较少。液固流化床的放大、设计和运行主要取决于对颗粒力学行为和流动特征（如颗粒分布、流动形态和颗粒混合状态）的准确预测。但是由于流化床内颗粒流体系统具有结构非均匀性、状态多值性、结构突变和结构的多尺度特征[3]，迄今为止仍然没有一套完整的理论体系来描述流化床内颗粒流体系统的动态特性，更缺乏液固流化床的放大与设计的通用方法，因此国际上此领域的研究受到学者的广泛关注[4-5]。

在流化床的研究中，实验方法可以获得较为可信的结果。但是，受限于实验条件和测试水平，实验测试不但成本高昂，而且很难获得颗粒在微观尺度上的运动信息。随着计算机技术的快速发展，数值模拟方法成为研究流化床系统的一个重要手段[6]。长期以来，液固两相流的模拟主要采用的是Euler-Euler双流体模型[7-8]。该方法将颗粒相处理为连续的拟流体，但这一假设从本质上削弱了模拟液固两相系统中非均匀结构的真实性。而Euler-Lagrange法可以很好地考虑液固两相系统中非均匀结构特性，并且可以获得丰富的颗粒微观信息，目前已被广泛应用于流化床的模拟领域[9-11]。

在实际工业应用中，单一粒度的颗粒系统是没有的，几乎都是由多种粒度组成的混合颗粒体系。颗粒粒径分布（PSD）对颗粒的流化行为有着很重要的影响。孙国刚等[12]的实验表明，对于存在粒度级配的颗粒群如果仅仅用单一的平均粒径，很难全面描述其内部复杂的流体动力学行为，应该要考虑粒径分布的影响。国内外很多学者对多组分颗粒体系进行了研究[13-15]，但是这些研究成果还是主要集中在气固流化床领域。鉴于此，以液固流化床为研究对象，采用CFD-DEM模拟方法，对二元混合、窄级配与宽级配3种粒度级配方式进行模拟，分别研究粒度级配对颗粒分布、颗粒速度、颗粒温度波动以及颗粒混合度的影响。

1 数学模型

1.1 连续相控制方程

连续性方程为

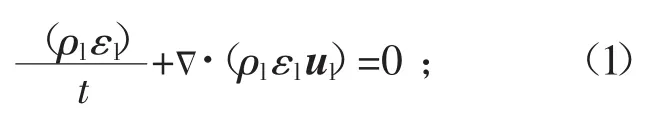
动量方程为

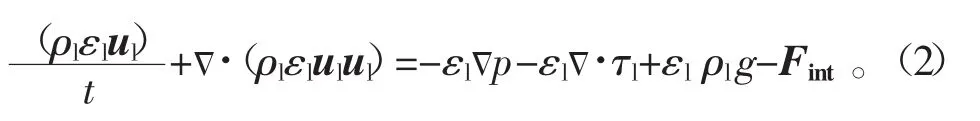
式中：ρl为液相密度；εl为液相体积分数；ul为液相速度；p为压力；τl为液相剪切应力张量，其定义为

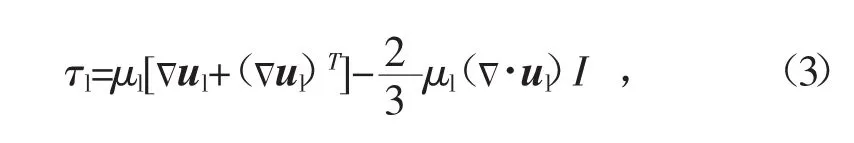
式中：μl是液相的剪切黏度；g是重力加速度。Fint为颗粒对流体的作用力，其计算公式为

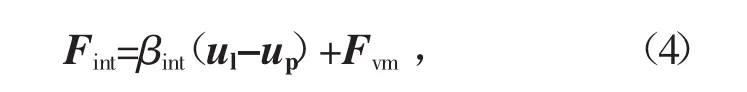
式中：βint为固相与液相间的曳力系数，βint（ul-up）、Fvm分别为曳力、虚拟质量力。

1.2 颗粒相控制方程

假设颗粒形状为球体，颗粒相的控制方程可用牛顿第二定律进行描述。每个颗粒都有平动和转动2种运动类型，其计算公式为

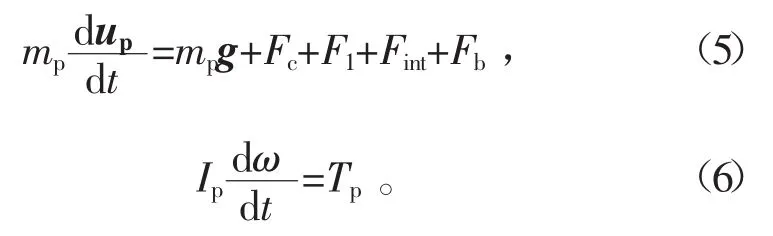
式中：mp和up是颗粒的质量和速度；式（5）右边各项分别为颗粒的重力、接触碰撞力、润滑力、相间力和浮力；Ip是颗粒的转动惯量；ω是颗粒的角速度；Tp是由颗粒切向接触力引起的转矩。

1.2.1 接触碰撞力

颗粒接触模型如图1所示。颗粒与颗粒、颗粒与壁面之间的接触力采用Hertz-Mindlin软球接触模型。接触力由法向力Fcn和切向力Fct组成，计算公式为

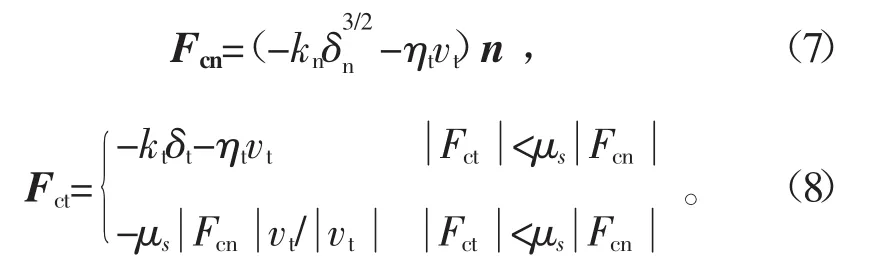
式中：k和η分别为弹性系数和阻尼系数；δ为重叠量；v为相对速度；μs为静摩擦系数。

1.2.2 润滑力

考虑到液固两相流颗粒流动的特殊性，故在经典的Hertz-Mindlin接触模型的基础上，考虑增加一个润滑力来表征颗粒之间填隙流体对颗粒碰撞的影响，如图1所示。当颗粒相互远离时，液体将流入颗粒间的缝隙内；当颗粒相互靠近时，液体将从缝隙内流出。流体的运动将产生一个压力梯度和黏性应力，它们累积后作用于颗粒上。此力将抑制颗粒间的分离。当2个颗粒相互靠近时，润滑力演变为排斥力；当相互远离时，润滑力演变为吸引力。润滑力[16]的计算公式为

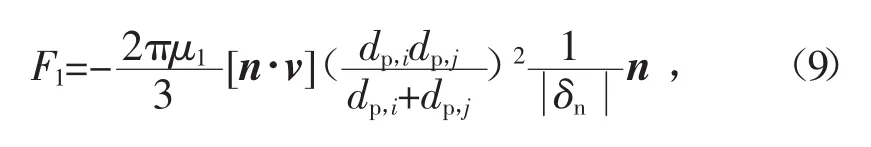
式中：v为2个颗粒的相对滑动速度；dp，i为i颗粒粒径。从润滑力的表达式中可以看出，当2个颗粒距离无限近的时候，润滑力会阻止2个颗粒的接触，并且会发散到无穷大。但是实际情况下，颗粒上还有其他作用力，并且颗粒表面也是粗糙的，所以在润滑力达到理论的极值之前，颗粒就会发生接触。为了模拟真实情况，所以设置截止距离δn＞0.001dp，来防止润滑力计算发散。

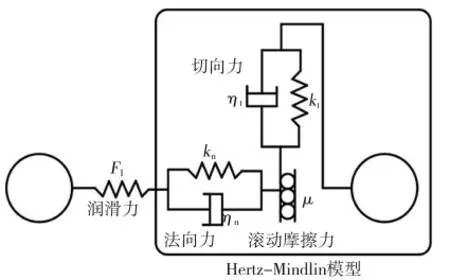
图1 颗粒接触模型Fig.1 Model of contact force between two particles

1.2.3 浮力

在液固两相流中，由于液体的密度相较于气体较大，所以液体对颗粒的浮力更加重要，浮力的计算公式为

1.3 相间耦合方程

颗粒流体系统的相间作用力很复杂，包括曳力、虚拟质量力、Magnus力、Saffman力、Basset力等。由于液体有较高的密度和黏度，因此本文中的相间耦合模型中考虑了曳力和虚拟质量力，而且在流化床中其他力与这2种力相比都较小，可以忽略。

1.3.1 虚拟质量力

在液固两相流中，颗粒相对于流体加速运动时，必将带动其周围的部分流体产生扰动，使其加速。对于球形颗粒，虚拟质量力的计算公式为

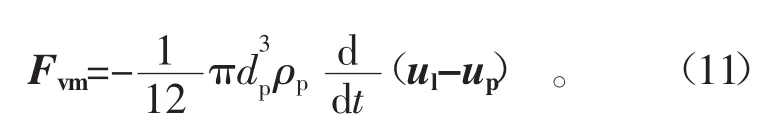
1.3.2 曳力

采用Lu等[17]所提出的Huilin-Gidaspow曳力模型，该模型避免了Wen&Yu和Ergun模型在孔隙率为0.8处的不连续性，通过引入函数让曳力模型变成一条光滑的曲线。Huilin-Gidaspow曳力模型中的曳力系数计算公式为

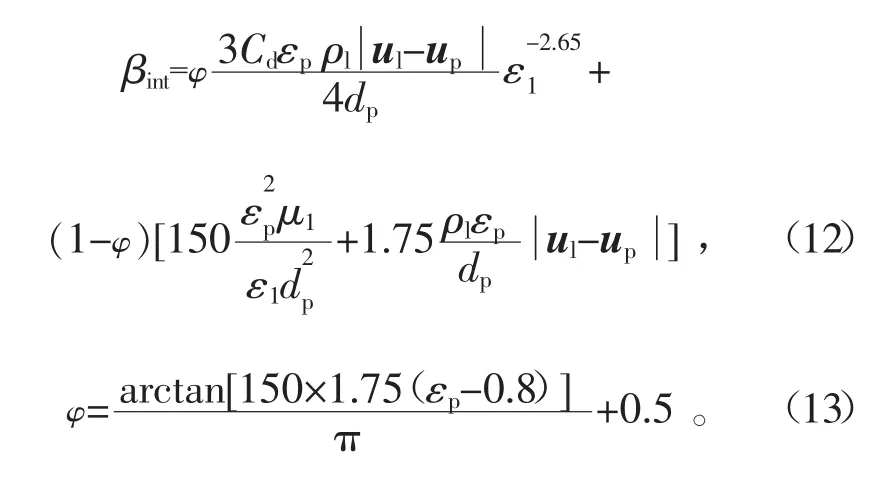
单颗粒曳力系数Cd和Reynolds数Re的一般关系为

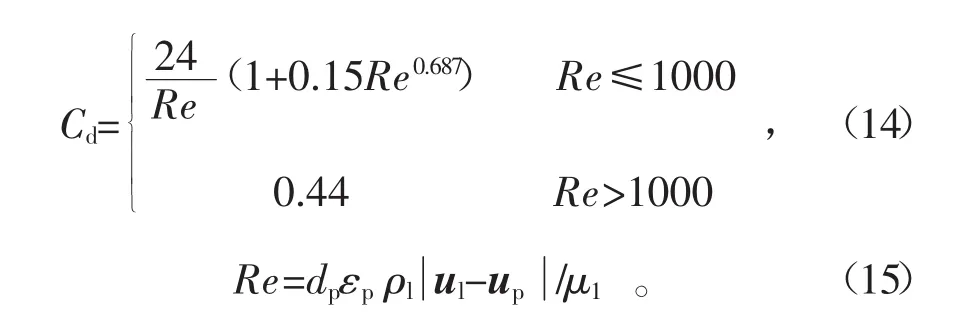
1.4 数值模拟参数及边界条件

三维流化床几何模型如图2所示，模型直径为140 mm，高度为1 000 mm。颗粒平均粒径和密度分别为3 mm和2 500 kg/m3。初始条件下，颗粒在床层内堆积形成一定高度，床层颗粒总质量为9.7 kg。采用速度入口和压力出口边界条件，入口处液相速度假设是均匀分布，液相在壁面处采用无滑移边界条件。模拟参数如表1所示。采用Gambit进行网格划分，网格类型选择Hex或Wedge，网格尺寸为10 mm。采用MFIX-DEM开源代码进行模拟。

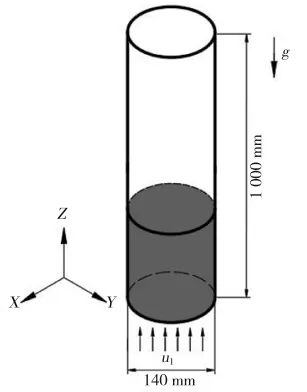
图2 三维流化床几何模型Fig.2 3D fluidized bed geometry model

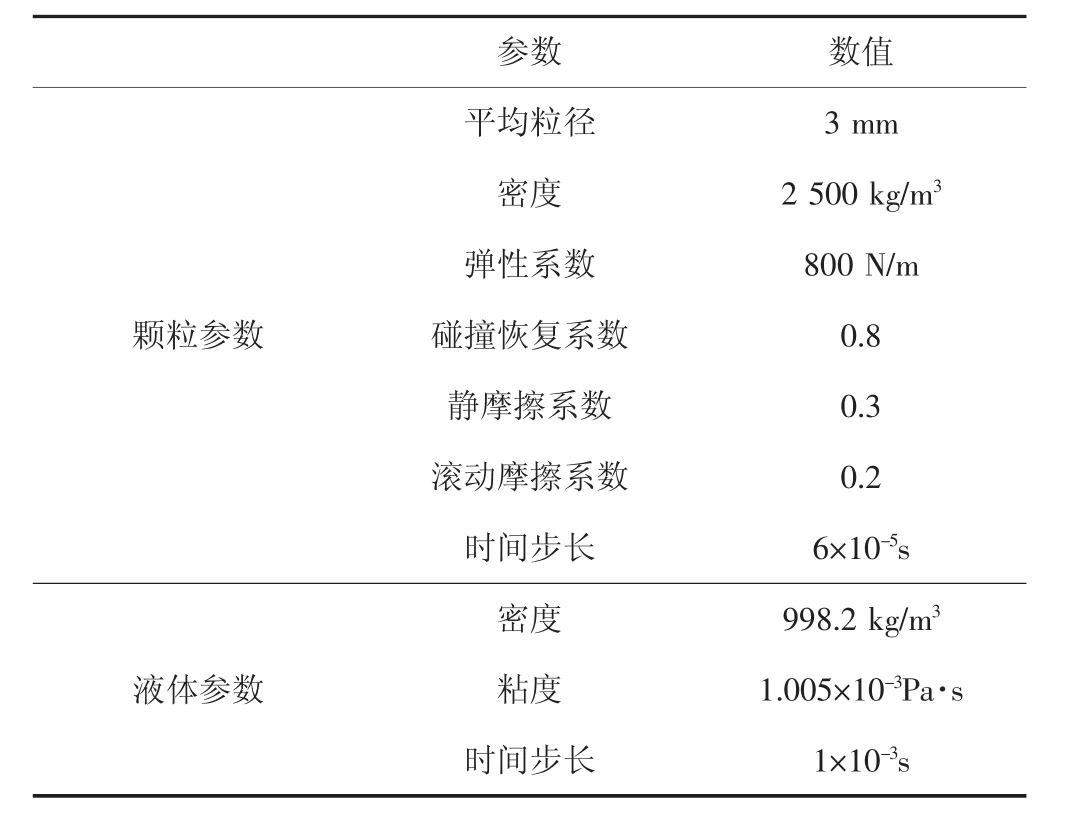
表1 模拟参数Tab.1 Parameters used in simulations

2 模型验证

Limtrakul等[18]采用计算机辅助放射性示踪粒子成像技术（CARPT）和射线计算机辅助层析成像技术（CT）测量了液固流化床的轴向速度和固体体积分数，实验所用的床体直径为1 40mm，高度为1 500 mm，颗粒粒径为3 mm，密度为2 500 kg/m3，液体表观流速为0.07 m/s。为了验证模型的有效性，将模拟结果与Limtrakul等的实验结果和Wang等[16]采用二维模型的模拟结果进行对比。

图3和图4分别为颗粒轴向速度和颗粒浓度的径向分布。从图中可以看出，模拟结果与Limtraku的实验结果吻合较好。而Wang模拟的是二维流化床，颗粒被简化为一个圆盘，缺少了一个维度上的信息，对颗粒运动产生了明显影响，所以模拟结果误差很大。

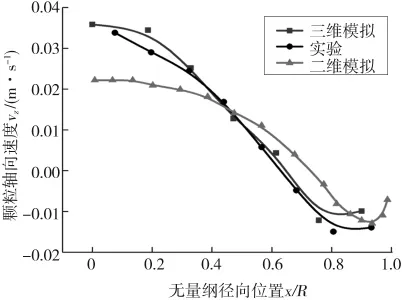
图3 颗粒轴向速度的径向分布Fig.3 Radial distribution of axial velocity of particles

3 粒度级配颗粒流动特性的模拟

3.1 颗粒粒径分布

为了研究液固流化床内粒度级配颗粒的流动特性，设计了3种不同粒径分布的颗粒组合，包括二元混合颗粒、正态分布颗粒（窄级配）以及均匀分布颗粒（宽级配），3种分布类的颗粒平均当量直径均为3 mm。模拟所用颗粒的粒径分布如表2所示。

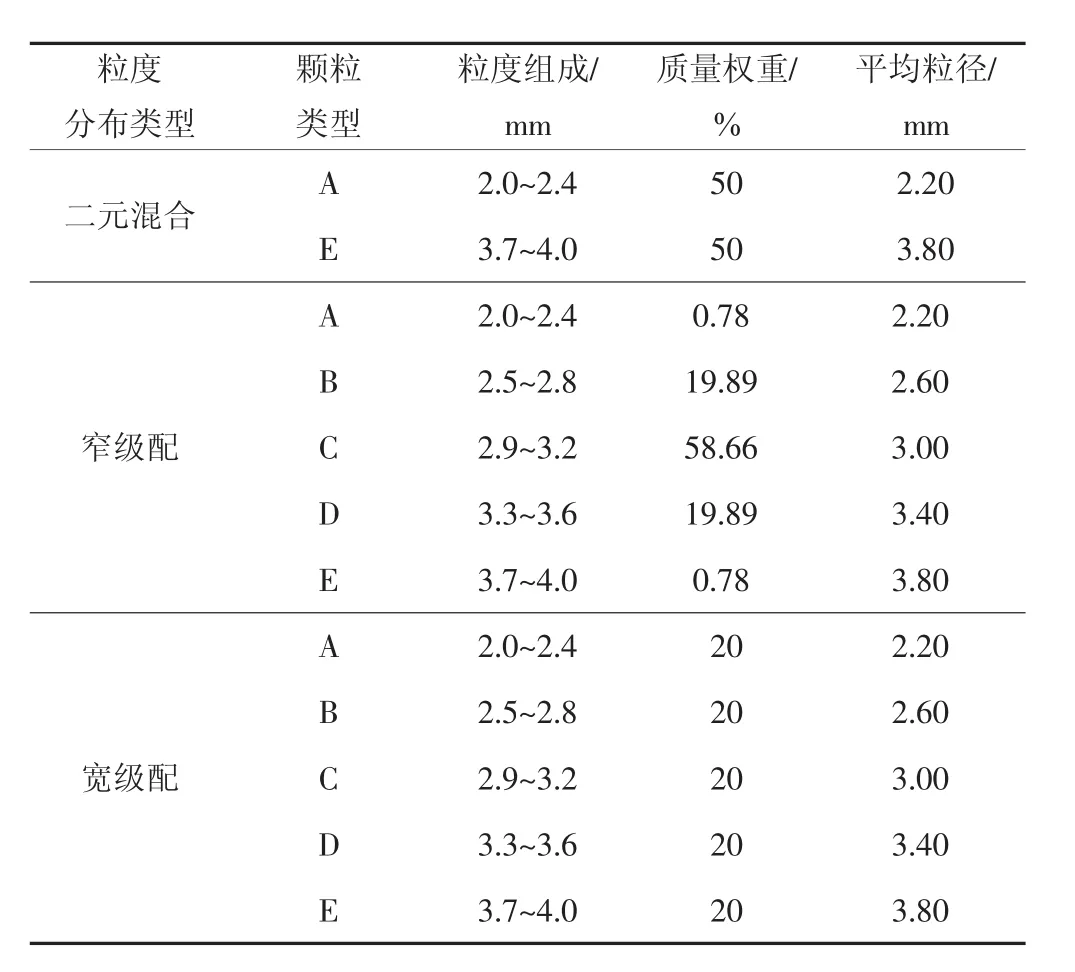
表2 颗粒粒径分布Tab.2 Particle size distribution

3.2 模拟结果

3.2.1 颗粒分布分析

为了研究3种不同的粒度级配方式对液固流化床内颗粒移动及分布情况的影响，将A、B、C、D、E 5种颗粒分别用不同的颜色表示。在液体流速为0.1 m/s条件下，3种不同粒度级配在0～6 s内的颗粒分布如图5所示。

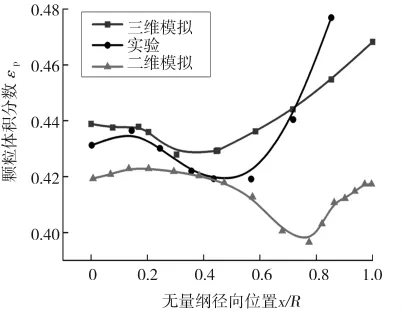
图4 颗粒浓度的径向分布Fig.4 Radial distribution of particle concentration

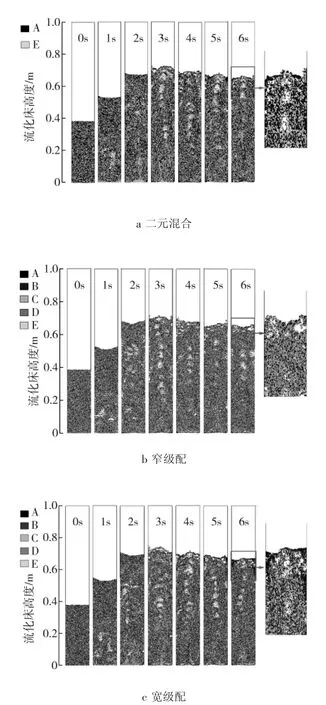
图5 粒度级配对颗粒分布的影响Fig.5 Influence of particle size distribution on particle distribution

从图可以看出，在t=0 s时刻，颗粒在堆积形成的床层内均匀混合。随着时间的推移，颗粒在流体的作用下，床层均匀向上膨胀，不同尺寸的颗粒逐渐分层。床层底部有小液泡产生，并逐渐向上运动，运动的过程中液泡不断融合、破裂和重新产生。在4 s以后，床层高度基本保持不变，由此可以认为流化床在4 s以后达到稳定状态。

从图5中还可以看出，二元混合和宽级配流化床的上部区域均有黑色的小颗粒聚集，这是由于这2种粒度级配方式中小颗粒的比例比较大。颗粒所受的曳力与粒径的平方成正比，颗粒的重力却与粒径的3次方成正比。当颗粒粒径减小的时候，重力减小的速度远大于曳力减小的速度，小颗粒的曳力会大于重力，所以小颗粒会更加容易的往上部运动。该现象表明二元混合和宽级配这2种粒度级配方式更容易产生颗粒的偏析。

为了定量研究流化床内颗粒的分层情况，将流化床分成3个区域，每个区域高度为0.2 m，研究不同高度处的大颗粒与小颗粒分布情况。3种粒度级配方式中大颗粒与小颗粒在不同高度的分布如图6—8所示。

从图6a、7a、8a中可以看出，不同区域的小颗粒质量变化一直处于波动过程，且在床层上部区域小颗粒质量都呈现出明显的增大趋势。这说明由于小颗粒具有较好的流动特性，会在整个床层中进行循环流动，即由上部区域进入下部区域，再由下部区域流动到上部区域。但是小颗粒的总体运动趋势是向床层的上部聚集。相反，从图6b、7b、8b中可以看出，床层下部区域大颗粒质量呈现出明显的增大趋势，且增大趋势比较平缓。这表明大颗粒的流动特性较差，从床层上部一直往下部运动。图7中还反应出窄级配中大颗粒与小颗粒在不同高度处的质量波动要比二元混合和宽级配更加剧烈。

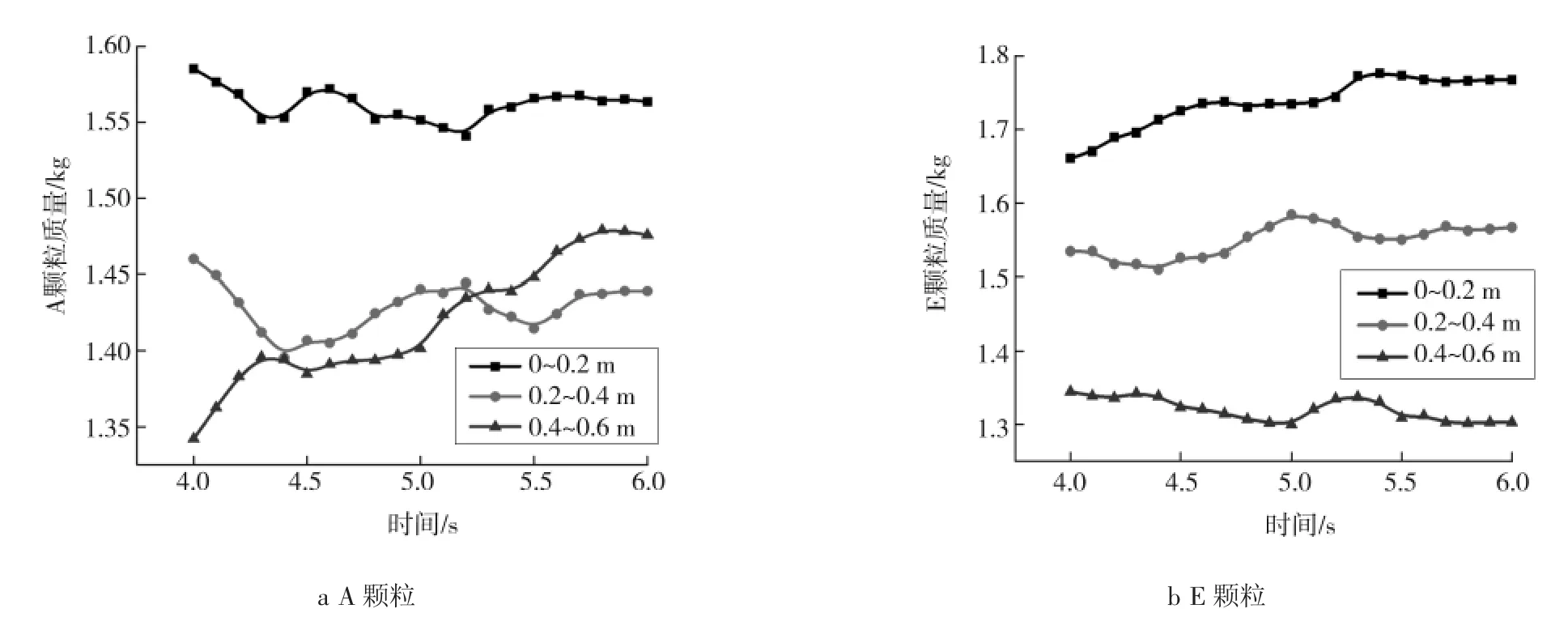
图6 二元混合中大颗粒与小颗粒在不同高度的分布Fig.6 Distribution of large particles and small particles at different heights in binary mixture

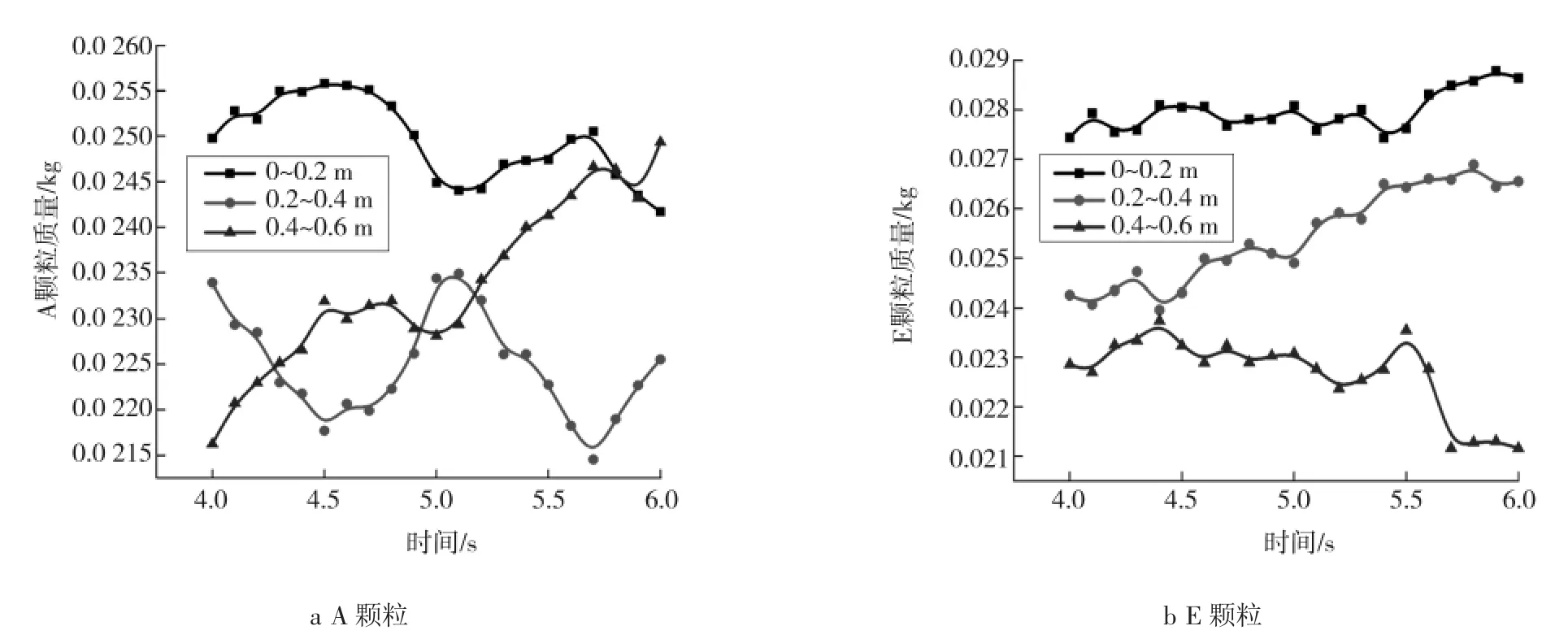
图7 窄级配中大颗粒与小颗粒在不同高度的分布Fig.7 Distribution of large particles and small particles at different heights in narrow size distribution

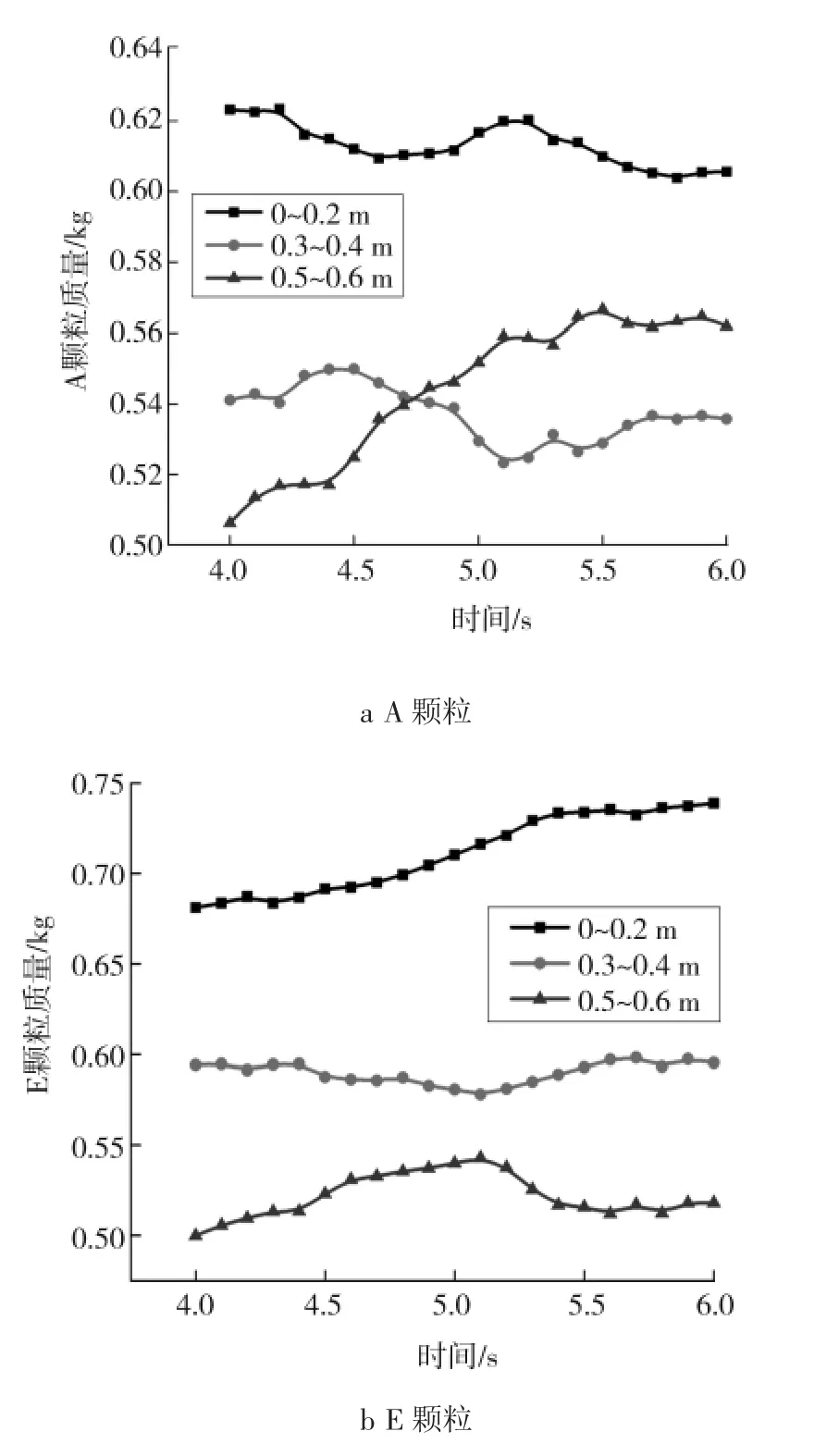
图8 宽级配中大颗粒与小颗粒在不同高度的分布Fig.8 Distribution of large particles and small particles at different heights in wide size distribution

3.2.2 颗粒速度分布分析

粒度级配对颗粒轴向速度的影响如图9所示。从图可以看出，所有的曲线均表现出相同的趋势：沿着径向方向颗粒轴向速度呈现出中心高，边壁低的不均匀分布，说明颗粒流动形式为典型的环核流动结构形式。产生环核流动的主要原因是液体径向速度分布不均匀，导致颗粒在不同位置所受到的曳力不同。在中心位置液体的流速大，对颗粒的曳力也大，所以颗粒速度较高；在壁面位置，液体速度降低，并且颗粒还受到边壁的阻滞作用的影响，使得颗粒速度出现负值。从图9b中可以看出，窄级配颗粒的轴向速度在不同高度差异不大，这与Roy等[19]对单一粒径颗粒的实验结果相似，这说明窄级配表现出单分散颗粒的运动特性。而从图9a和9c中可以看出，二元混合和宽级配的轴向速度在不同高度上差异较明显，这是由于粒径分布较宽，导致在不同高度上颗粒分布不均匀，从而使得颗粒轴向速度在不同高度上出现差异。

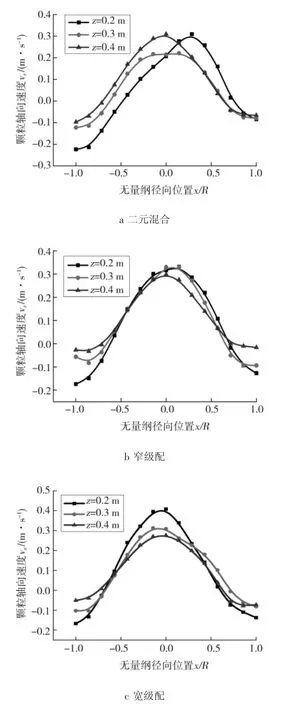
图9 粒度级配对颗粒轴向速度的影响Fig.9 Influence of particle size distribution on particle axial velocity

3.2.3 颗粒温度波动分析

颗粒温度波动是基于颗粒随机波动速度的统计函数，颗粒温度波动与气体动力学理论中的温度类似，是度量颗粒碰撞强度的函数，同时也是测量颗粒系统的动力学行为最重要的参数之一。在三维系统中，可以定义为

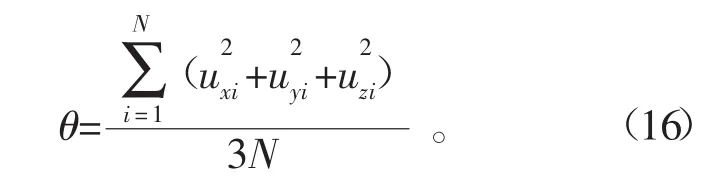
式中：uxi、uyi和 uzi分别为 i颗粒 x、y、z 3 个方向的随机波动速度，是瞬时速度和平均速度的差值。N为颗粒个数。

图10为粒度级配对颗粒温度波动的影响。从图中可以看出，颗粒温度波动主要集中在颗粒体积分数为0.3～0.5这个区间，而在这个区间的两侧颗粒温度波动均较低。这是由于当颗粒体积分数较低的时候，颗粒个数较少，所以颗粒间发生碰撞的概率也很小；而颗粒在较高的体积分数下，由于颗粒之间接触十分紧密，阻碍了颗粒的相互运动，从而使颗粒的脉动程度降低，颗粒温度波动也减小。从图中还可以看出，3种粒度级配的温度波动关系：窄级配＞宽级配＞二元混合。这是由于窄级配中的大颗粒比例较少，能表现出很好的流化性能，导致颗粒的脉动程度也较高，从而使窄级配有较大的颗粒温度波动。由于窄级配中颗粒有较大的温度波动，因此在不同高度处，窄级配颗粒质量波动会比二元混合和宽级配更加剧烈。

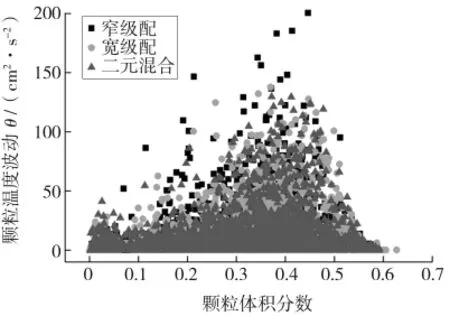
图10 粒度级配对颗粒温度波动的影响Fig.10 Influence of particle size distribution on particle temperature

3.2.4 颗粒混合度分析

为了定量分析不同种颗粒的混合程度，引入Lacey[20]混合指数M对3种粒径分布下的颗粒混合与分离情况进行分析。M表达式为

式中：S2为2种颗粒的实际混合方差；为完全分离时的方差，S02＝q（1-q），q为其中一种颗粒的体积分数；SR2为完全混合时的方差，SR2＝ q（1-q）/N，N 为一个样本内的平均颗粒数目。

图11为粒度级配对颗粒混合指数的影响。图11a为宽级配的混合指数变化，从图中可以看出，A颗粒和E颗粒、B颗粒和E颗粒之间的混合指数下降幅度较大，均降低到了0.9以下；A-C、B-D、C-E和A-D之间的混合指数也减小到了0.9～0.95之间；而A-B、B-C、D-E和C-D之间的混合指数从混合指数为1的均匀混合状态降低到一定水平，不再进一步减小，只是略有波动，且混合指数均在0.95以上。

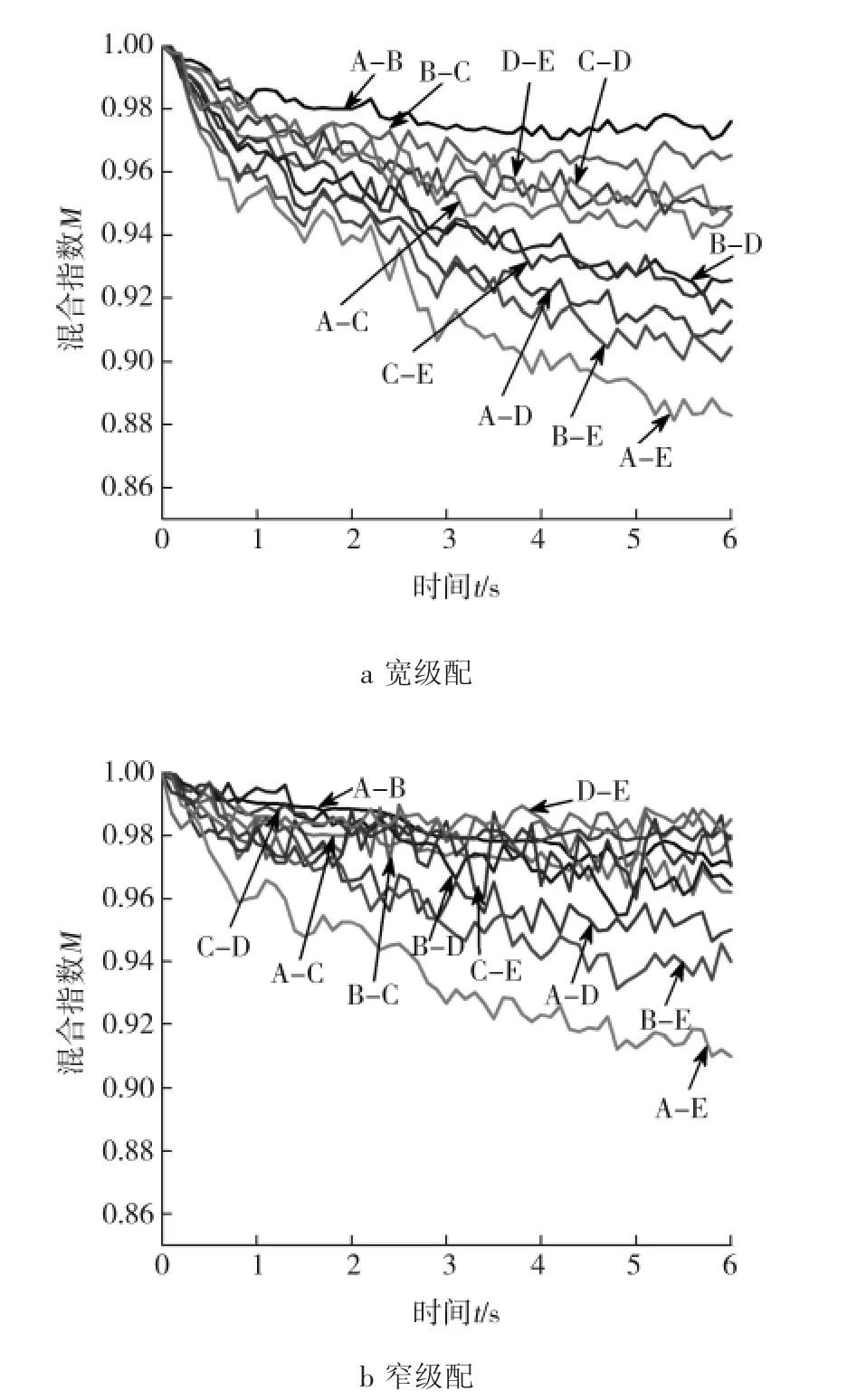
图11 粒度级配对颗粒混合指数的影响Fig.11 Influence of particle size distribution on mixing index

这是由于小颗粒较容易往床层上部运动，而大颗粒则有向床层下部聚集的趋势，故2种颗粒粒径差距越大，越容易分离，而2种颗粒粒径越接近，越难分离，混合程度越好。图11b为窄级配的混合指数变化，从图中可以看出，颗粒间的混合指数下降幅度均有所减小，A-E、B-E和A-D之间的混合指数与其他颗粒相比下降幅度还是较大，但是均在0.9以上。这说明，由于窄级配颗粒温度波动较大，颗粒波动较剧烈，因此窄级配与宽级配相比，床层内颗粒整体上混合的较均匀，颗粒偏析情况不明显。

4 结论

采用CFD-DEM耦合方法模拟了三维液固流化床系统，在模型中考虑了润滑力对颗粒运动的影响。通过与Limtraku的实验结果对比，发现本文中所采用的数学模型可以有效模拟液固流化床系统。随后研究了二元混合、窄级配与宽级配3种粒度级配方式对颗粒流动特性的影响，得到如下结论：

1）大颗粒有向床层下部运动的趋势，而小颗粒则有向床层上部聚集的趋势，且小颗粒的流动特性要比大颗粒好。

2）与窄级配相比，二元混合和宽级配的轴向速度在不同高度上差异较明显，且颗粒温度波动也较小。

3）采用混合指数定量考察流化床内颗粒的混合状态，发现2种颗粒粒径差距越大，越容易分离，而粒径越接近，越难分离，混合程度越好；窄级配与宽级配相比，床层内颗粒整体上混合的较均匀，颗粒偏析情况不明显。

参考文献（References）：

[1]WU C，XIAO M，CHEN S，et al.Application of fluidization technology in productions of cemented carbides[J].International Journal of Refractory Metals&Hard Materials，2014，46（1）:188-194.

[2]BELLO M M，RAMAN A A A，PURUSHOTHAMAN M.Applications of fluidized bed reactor in wastewater treatment A review of the major design and operational parameters[J].Journal of Cleaner Production，2016，141:1492-1514.

[3]李静海，欧阳洁，高示秋，等.颗粒流体复杂系统的多尺度模拟[M].北京:科学出版社，2005:12-25.

[4]PAN H，CHEN X Z，LIANG X F，et al.CFD simulations of gas liquid solid flow in fluidized bed reactors-a review[J].Powder Technology，2016，299:235-258.

[5]LIU G，YU F，LU H，et al.CFD-DEM simulation of liquidsolid fluidized bed with dynamic restitution coefficient[J].Powder Technology，2016，304:186-197.

[6]任立波.稠密颗粒两相流的CFD-DEM耦合并行算法及数值模拟[D].山东：山东大学，2015.

[7]PAN H，LIANG X，LUO Z.CFD modeling of the gas solid two-fluid flow in polyethylene FBRs:from traditional operation to super-condensed mode[J].Advanced Powder Technology，2016，27（4）:1494-1505.

[8]FENG X，LI X，CHENG J，et al.Numerical simulation of solid-liquid turbulent flow in a stirred tank with a two-phase explicit algebraic stress model[J].Chemical Engineering Science，2012，82:272-284.

[9]OZEL A，MOTTA J C B D J C，ABBAS M，et al.Particle resolved direct numerical simulation of a liquid-solid fluidized bed:comparison with experimental data[J].International Journal of Multiphase Flow，2017，89:228-240.

[10]朱卫兵，李锦时，王猛，等.提升管内湿颗粒流动特性的离散元模拟[J].中国电机工程学报，2013，33（35）:81-88.

[11]王猛，朱卫兵，孙巧群，等.提升管内气固流动特性的离散元模拟[J].化工学报，2013，64（7）:2436-2445.

[12]孙国刚，李静海.粒径分布对循环床内颗粒速度分布的影响[J].中国粉体技术，1998，4（1）:1-5.

[13]赵永志，郑津洋.宽粒径分布流化床的微观尺度模拟与分析[J].中国电机工程学报，2007，27（35）:55-61.

[14]GAUTHIER D，ZERGUERRAS S，FLAMANT G.Influence of the particle size distribution of powders on the velocities of minimum and complete fluidization[J].Chemical Engineering Journal，1999，74（3）:181-196.

[15]WANG S Y，LU H L，LI X，et al.Discrete particle simulations for flow of binary particle mixture in a bubbling fluidized bed with a transport energy weighted averaging scheme [J]. Chemical Engineering Science，2009，64（8）:1707-1718.

[16]WAMG S，GUO S，GAO J，et al.Simulation of flow behavior of liquid and particles in a liquid solid fluidized bed[J].Powder Technology，2012，224:365-373.

[17]LU H L，GIDASPOW D.Hydrodynamics of binary fluidization in a riser:CFD simulation using two granular temperatures[J].Chemical Engineering Science，2003，58（16）:3777-3792.

[18]LIMTRAKUL S，CHEN J，RAMACHANDRAN P A，et al.Solids motion and holdup profiles in liquid fluidized beds[J].Chemical Engineering Science，2005，60（7）:1889-1900.

[19]ROY S，SAI P S T，JAYANTI S.Numerical simulation of the hydrodynamics of a liquid solid circulating fluidized bed[J].Powder Technology，2014，251:61-70.

[20]LACEY P M C.Developments in the theory of particle mixing[J].Journal of Applied Chemistry，1954，4（5）:257-268.