机械式高速混合机内部多粒径颗粒混合特性仿真

谢红笑，刘雪东，尹传忠，马 乾，温传美

（常州大学a.机械工程学院；b.江苏省绿色过程装备重点实验室，江苏常州 213000）

干燥粉体物料的混合广泛应用于化工、饲料、制药、食品、材料（粉体冶金）等领域。2种或2种以上不同特性的物料，在机械或是其他外力的作用下相互进入到对方物料所在区域，物料颗粒的运动速度、方向、位置不断发生变化，使各特性的物料颗粒在总体区域及各个子空间内分布均匀，这样的一个过程就是混合[1]。机械式混合具有混合快、混合均匀、机器操作方便、布置灵活、对环境无污染、维修简单等突出优势[2-3]。搅拌桨与高速飞刀是高速混合机进行颗粒混合的核心构件，研究颗粒的运动行为对于提高高速混合机混合质量和混合效率具有重要意义[4-5]。

Alian等[6]开展了一系列颗粒混合实验，通过改变初始装填方式、物料装填系数、转速等条件，探究固体颗粒搅拌速率的变化规律和混合均匀度的变化规律。Veerakiet等[7]通过改变搅拌桨的桨叶数研究混合扩散系数的变化规律，进而提高混合机的混合性能。Halidan等[8]采用离散单元法（DEM）研究立式高速混合机内颗粒的大小与密度对颗粒运动行为的影响，进而提高高速混合机的混合性能。国内外学者的实验或数值仿真重点多集中在高速混合机的混合效率以及混合均匀度，对高速混合机内的颗粒运动规律探究较少，对多粒径颗粒的混合研究更少。鉴于此，采用离散单元法对高速混合机内部多粒径颗粒的混合过程进行数值模拟，对探索颗粒运动特性的研究以及优化高速混合机结构设计具有一定的参考意义。

1 计算域模型及设置

1.1 模型建立

机械式高速混合机结构示意图如图1所示。釜体呈圆筒形，为多层结构，分内外层、夹套和隔热层；搅拌桨由驱动轴带动旋转，其驱动装置由调速电机、传动轴、皮带轮等组成。

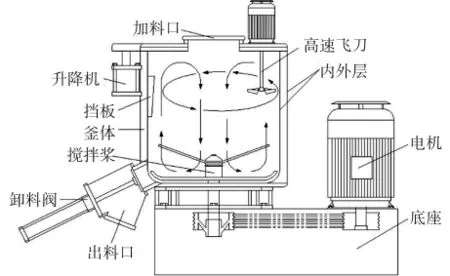
图1 高速混合机结构示意图Fig.1 Schematic of high speed mixer

采用离散单元软件EDEM[9-10]建立高速混合机仿真计算模型，如图2所示。模型主要由搅拌桨、高速飞刀、釜体、挡板四部分组成。其中釜体直径Φ=180 mm，高度H=180 mm；搅拌桨直径db=172 mm；高速飞刀直径dc=37 mm；挡板长度L=50 mm。

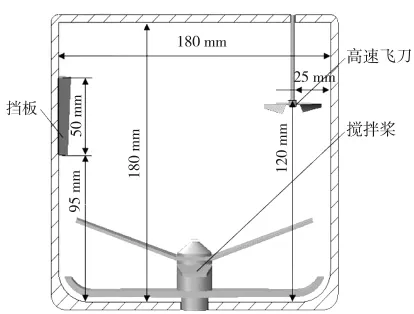
图2 高速混合机仿真计算模型Fig.2 Simulated computational model of high speed mixer

1.2 控制方程

离散单元法是根据离散单元间的相互作用和牛顿第二定律，通过不断循环计算获得颗粒在每个时间步的位置信息和速度信息，同时能够获得颗粒间发生接触碰撞时的接触力，得到颗粒运动的详细微观数据信息，进而建立宏观运动与微观行为的联系，更好地掌握颗粒运动规律[11]。图3为离散单元法接触模型，颗粒与颗粒间、颗粒与几何体之间均采用振动方程进行模拟，接触模型采用Hertz-Mindlin接触模型，法向部分来自Hertz接触理论，切向部分则来自Mindlin接触理论[12]。

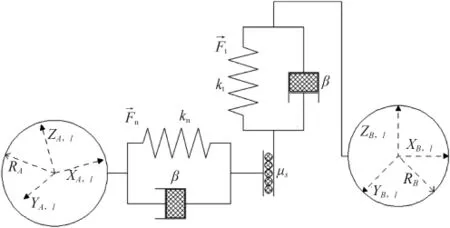
图3 离散元方法接触模型Fig.3 Contact model in DEM

颗粒间法向力和法向阻尼力为

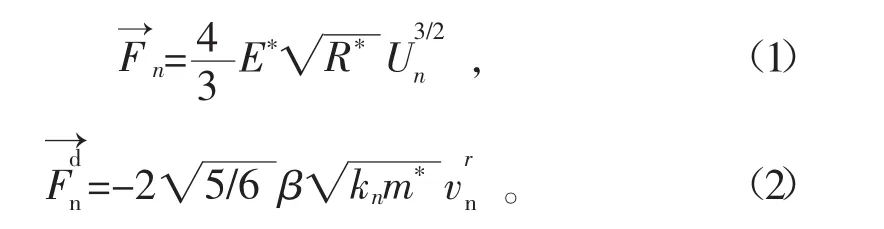
式中：E*为等效弹性模量，MPa；R*为等效粒子半径，m；Un为颗粒的法向重叠量，m；β为阻尼系数；kn为法向刚度N/m；m*为等效质量，kg；为相对速度的法向分量值，m/s。

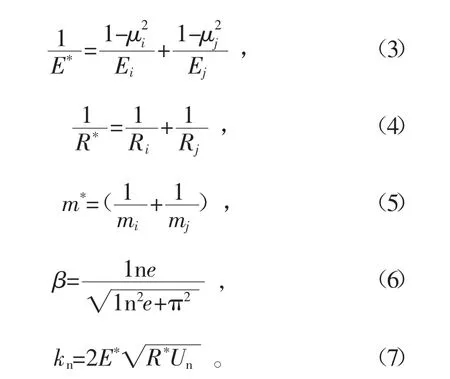
式中：E 为颗粒的弹性模量，MPa；μ 泊松比；Ri、Rj为球体接触半径，m；mi、mj为颗粒 i，j的等效质量，kg。

颗粒间的切向力和切向阻尼力为

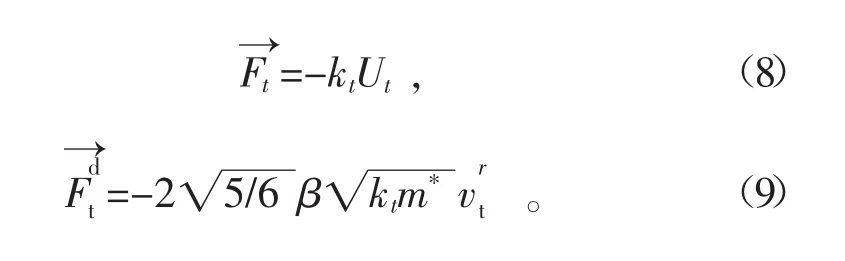
其中：

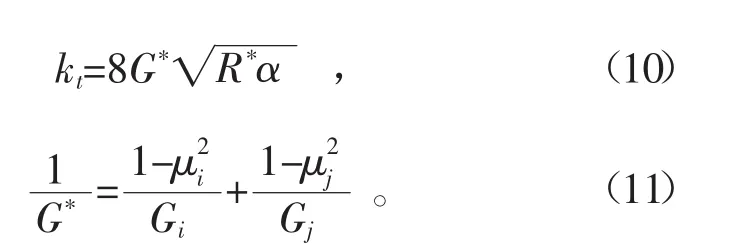
式中：Ut为切向重叠量，m；kt为切向刚度，N/m；G 为等效剪切模量，MPa为切向相对速度，m/s。

1.3 模拟参数的设置

DEM设置。采用模拟软件EDEM 2.7.1，EDEM的相关参数设置[13]如表1所示。混合对象为质量比为1∶1∶1∶1 的 4 种均匀球形亚克力颗粒组成的颗粒群,每种颗粒质量为0.4 kg，颗粒直径分别为2、3、4、5 mm（颗粒数量分别为 79 577、23 578、9 947、5 092），并且以小粒径颗粒在下大粒径颗粒在上的原则依次填充，混合颗粒群的粒径分布如图4所示。混合过程中，搅拌桨转速为1 400 r/min；高速飞刀转速为3 000 r/min，转动方向与搅拌桨相同。

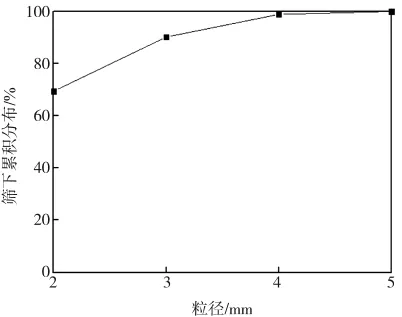
图4 混合颗粒群的粒径分布图Fig.4 Particle size distribution of mixing particle group

表1 EDEM参数设置Tab.1 Parameters setting of EDEM

1.4 混合质量评价

对整个高速混合机进行12×12×12的空间网格划分,细分网格如图5所示。以0.2 s为时间间隔将0～5 s不同时刻的各个网格中的颗粒总数以及每个网格中各种颗粒数量进行导出计算[14]。

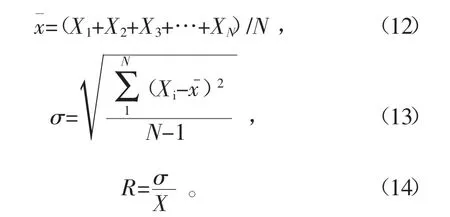
颗粒静止后的环形网格模型划分如图6所示。对每个网格区域内的颗粒数目进行统计，得到各区域内4种不同粒径颗粒的数目，并计算其绝对平均粒径 d[15]，计算公式为

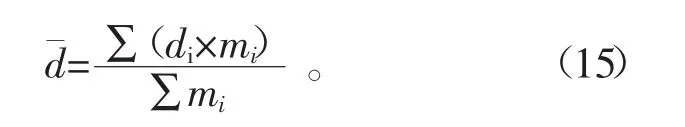
式中：di为颗粒 i的直径，m；mi为颗粒 i的质量，kg。为了表征颗粒静止后各个环形网格区域内颗粒粒度大小的差异，引入相对平均粒度，它是各区域内颗粒的绝对平均粒径与整个高速混合机内颗粒的绝对平均粒径的比值。

图5 细分网格Fig.5 The subdivided mesh

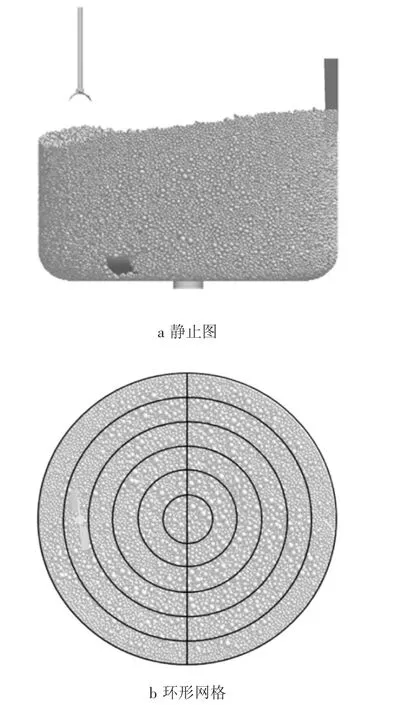
图6 颗粒静止后的环形网格模型Fig.6 Annular mesh model after particle mixing process

为量化高速混合机内部颗粒的偏析分布，统计如图6b所划分的环形网格区域内大颗粒的体积分数。使用不同网格区域内大颗粒所占体积分数之间的差值，表征高速混合机内各网格区域颗粒是否形成偏析结构。针对偏析结构，定义偏析指数SI：

即用大颗粒在第n个网格中的体积分数φn，与大颗粒在整个高速混合机内颗粒群的体积分数φ0之间差值的绝对值，来表示偏析程度。SI值越低，表明偏析程度越小。

2 结果与讨论

2.1 颗粒混合过程

2.1.1 颗粒混合均匀度

图7为离散系数随时间的变化规律。由图可知，离散系数随时间不断减小，混合均匀度不断提高，混合时间为3 s时，离散系数达到0.15，3 s后离散系数基本保持不变，颗粒混合均匀。

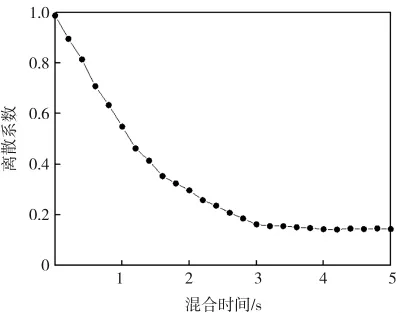
图7 离散系数随时间的变化规律Fig.7 Relative standard deviation of mixing with time

2.1.2 颗粒运动轨迹

图8为高速混合机内颗粒在0、0.5、1、3 s 4个不同时刻的混合状况，0 s时，4种颗粒几乎是完全分离的状态，随着搅拌桨与高速飞刀的转动，4种颗粒逐渐混合，最终获得一个均匀度高的混合物。

图8 不同时刻颗粒混合状况Fig.8 Movement condition of particles

图9为直径为4 mm和5 mm颗粒的速度矢量图。由图可知，高速旋转的搅拌桨借助表面与物料的磨擦力及侧面对物料的推力使物料沿搅拌桨切向运动，由于离心力的作用，又被抛向釜体内壁，并且沿壁面上升。一部分颗粒运动至高速飞刀位置被分散，另外一部分颗粒升高到一定高度时，由于重力作用又落回到搅拌桨中心，接着又被抛起，这种上升运动与切向运动结合，使物料处于连续的螺旋状上下运动状态。并且整个过程中伴随着碰撞、折射、反弹等剧烈运动。

图9 直径为4 mm和5 mm颗粒速度矢量图Fig.9 Velocity vector diagram of 4 and 5 millimeter particles

2.1.3 颗粒粒度分布及偏析行为

颗粒在不同区域内的相对平均粒径如图10所示。x＝0处为高速混合机对称中心，将各数值与1进行比较，其中，高速飞刀一侧自边缘往中心呈现出由小变大再变小的粒度分布，挡板一侧呈现由小变大再变小的粒度分布，颗粒相对平均粒径波动范围在-0.05～0.05之间，在颗粒静止过程中混合机边缘出现小颗粒增多现象。

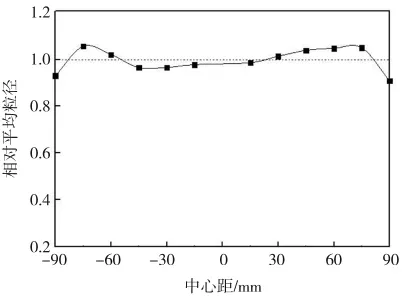
图10 颗粒在不同区域的相对平均粒径Fig.10 Relative to the average particle size in different regions

图11为颗粒在环形网格内的偏析指数分布，其值在0～0.07之间波动，相对于高速飞刀一侧，挡板一侧偏析指数波动稍大，并且位于高速混合机边缘部分偏析指数SI增大，出现少量小颗粒偏析现象。静止过程中，高速混合机挡板位置的特殊构造以及大小颗粒各异的流动行为差异导致了颗粒在挡板一侧和高速飞刀一侧之间存在不同的粒度偏析结构。

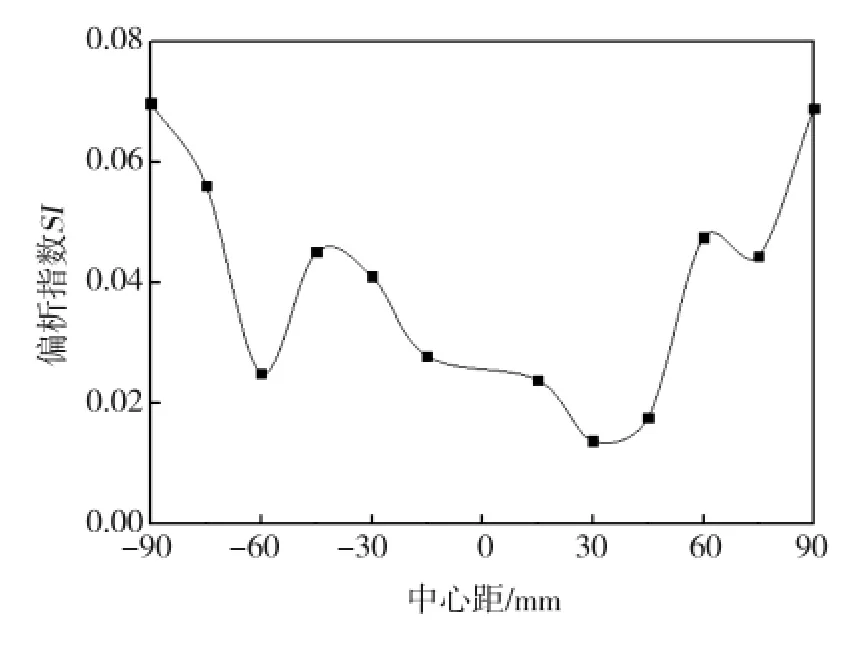
图11 颗粒在环形网格内的偏析指数分布Fig.11 The segregation index of particles in annular mesh

2.2 颗粒受力与速度分析

利用EDEM的后处理工具，将模型进行分层网格划分，如图12所示。研究不同高度和不同粒径颗粒的运动和受力情况，将数据进行分析整理得到颗粒的合力和速度的变化规律。

图12 分层网格Fig.12 Layered mesh

研究高速混合机内部颗粒的运动学特性分析对提高高速混合机性能具有重要意义。图13为颗粒平均速度与受力随高度的变化规律。颗粒运动的平均速度与受力的变化规律大致相同，颗粒的平均速度与受力在釜体底部最大，随着高度的升高，颗粒的速度与受力逐渐减小，并且，越高层颗粒速度与受力降低越慢。

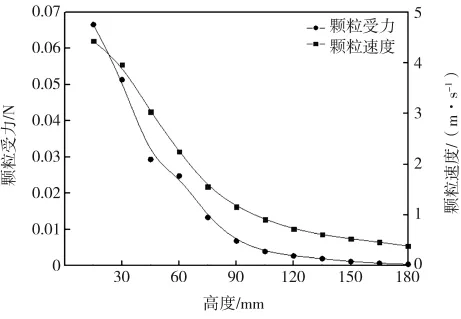
图13 颗粒平均速度和受力随高度的变化规律Fig.13 Average velocity and force of particles with height

图14为颗粒受力与速度随粒径的变化规律。由图可知，颗粒在运动过程中受力（重力除外）和速度的变化规律大致相同。随着颗粒尺寸的增大，颗粒的运动速度与受力逐渐增大。原因是颗粒的直径越大，体积越大，同一时刻可以与更多的颗粒发生碰撞运动，导致大颗粒受到的力较大。高速混合机内，颗粒速度随着粒径的增大，颗粒速度变大。这主要是由两方面原因造成：一方面，在封闭的高速混合机内单个大尺寸颗粒，所占空间较大，与更多颗粒发生碰撞的概率也大，周围的小尺寸颗粒在运动过程中受到大颗粒的阻碍，导致速度降低；另一方面，在混合过程中，搅拌桨与高速飞刀的机械能转化为颗粒的动能，如图15所示，大尺寸颗粒获得更高的能量，使得大尺寸颗粒运动速度较快。

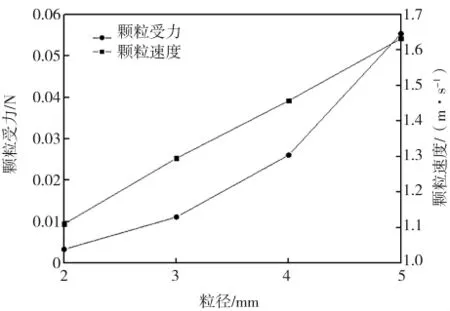
图14 颗粒受力与速度随粒径的变化规律Fig.14 The force and velocity of particles with diameter

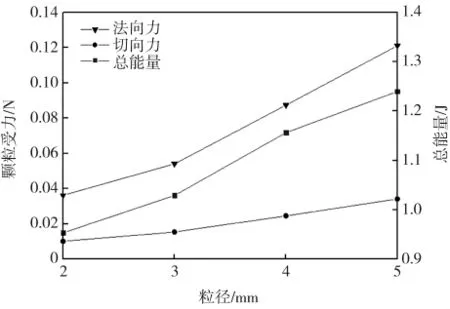
图15 法向力、切向力和总能量随粒径的变化规律Fig.15 Normal force,Tangential force and total energy of particles with diameter

图15为切向力、法向力和总能量随粒径的变化规律。随着颗粒直径的变大，颗粒法向力与切向力逐渐增大。颗粒法向力大于切向力，颗粒尺寸越大，法向力与切向力之间差距越大。原因是高速转动的搅拌桨使得颗粒受到离心力作用，使得颗粒被抛向釜体内壁，颗粒之间相互碰撞、挤压，颗粒尺寸越大，碰撞、挤压越明显。搅拌桨侧面对颗粒的推力使得颗粒沿切线方向快速转动，转动过程中阻力较小。

3 结论

采用离散单元法对机械式高速混合机内部4种不同粒径球形亚克力颗粒组成的颗粒群的混合过程进行数值模拟，得到如下结论：

1）颗粒在搅拌桨与高速飞刀共同作用下，呈现连续的螺旋上下运动状态，中心形成漩涡；

2）高速混合机的特殊构造以及大小颗粒各异的流动行为导致颗粒在挡板一侧和高速飞刀一侧之间存在不同的粒度偏析结构，静止过程中边缘出现少量小颗粒偏析现象；

3）颗粒混合主要集中在高速混合机中下部，颗粒受力与速度随着高度的增加不断减小，并且越高层颗粒受力与速度降低越慢；

4）颗粒在混合过程中，颗粒受力与颗粒速度随着颗粒尺寸的不断增大而增大；

5）高速旋转的搅拌桨使颗粒受较大离心力作用，颗粒法向力大于切向力，并且颗粒尺寸越大，法向力与切向力差距越大。

参考文献（References）：

[1]叶涛.多组分粉体混合过程的理论分析与实验研究[D].武汉：武汉理工大学，2009.

[2]ZHOU Y C，YU A B，STEWART R L，et al.Microdynamic analysis of the particle flow in a cylindrical bladed mixer[J].Chemical Engineering Science，2004，59（6）：1343-1364.

[3]陈俊英，李红伟.化工行业常用搅拌器研究热点[J].现代化工，2011，31（10）：12-16.

[4]王港，黄锐，陈晓媛，等.高速混合机的应用及研究进展[J].中国塑料，2001，15（7）：11-14.

[5]CHANDRATILLEKE G R，YU A B，STEWART R L，et al.Effects of blade rake angle and gap on particle mixing in a cylindrical mixer[J].Powder Technology，2009，193（3）：303-311.

[6]ALIAN M，FARHAD E M，SIMANT R，et al.Using discrete element method to analyze the mixing of the solid particles in a slant cone mixer[J].Chemical Engineering Research and Design，2015，93（1）：318-329.

[7]BOONKANOKWONG V，REMY B，KHINAST J G，et al.The effect of the number of impeller blades on granular flow in a bladed mixer[J].Powder Technology，2016，302（11）：333-349.

[8]HALIDAN M，CHANDRATILLEKE G R，CHAN S L I，et al.Prediction of the mixing behaviour of binary mixtures of particles in a bladed mixer[J].Chemical Engineering Science，2014，120（12）：37-48.

[9]周志勇.基于DEM的强力混合机混匀过程模拟及结构优化[D].湘潭：湘潭大学，2014.

[10]胡国明.颗粒系统的离散元素法分析仿真[M].武汉：武汉理工大学出版社，2010：1-3.

[11]SAKAI M，SHIGETO Y，BASINSKAS G，et al.Discrete element simulation for the evaluation of solid mixing in an industrial blender[J].Chemical Engineering Journal，2015，279（11）：821-839.

[12]CLEARY P W，SINNOTT M D.Assessing mixing characteristics of particle-mixing and granulation devices[J].Particuology，2008，6（6）：419-444.

[13]LIU W M，XU J，LIU X D.Numerical study on collision characteristics for non-spherical particles in venturi powder ejector[J].Vacuum，2016，131（5）：285-292.

[14]MUZZIO F J，LLUSA M，GOODRIDGE C L，et al.Evaluating the performance of a ribbon blender[J].Powder Technology，2008，186（3）：247-254.

[15]朱明华，杜屏，刘建波.高炉炉顶料罐装料过程计算及分析[C]//全国大高炉炼铁学术年会，2013：78-83.