理想气体状态方程的多种统计推导
任 青,杨文平
(山西大同大学物理与电子科学学院,山西大同037009)
为了明确,考虑单原子分子理想气体。单原子分子看作没有内部结构的质点,忽略分子间的相互作用,在没有外场时,其分子间的相互作用势为

即无引力的弹性质点模型[1]。
1 用玻尔兹曼统计求
其配分函数为
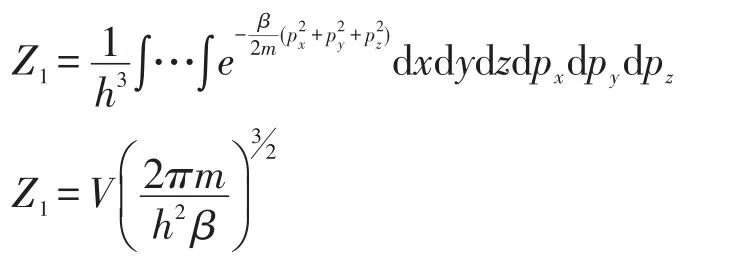
根据统计公式[2]

可得理想气体的压强p为
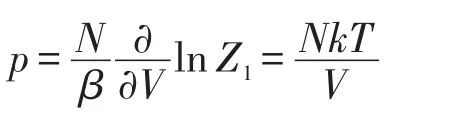
其中方程pV=NkT即为状态方程。
2 用微正则系综理论求
微正则系综,把系统看作整体,系统能量只有极小变化。在能量E到E+△E范围内的微观状态数为
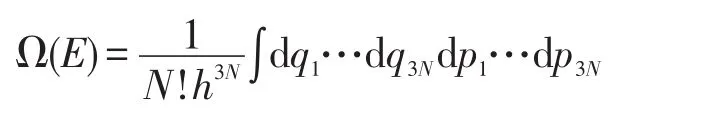
为了求Ω(E),首先计算能量≤某一数值E的微观状态数∑(E)[2]:
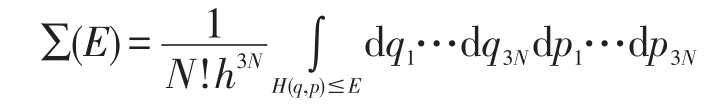
求得
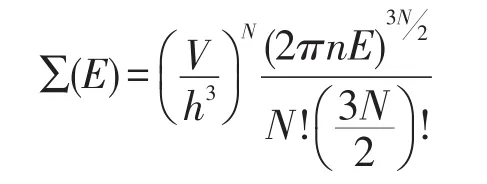
E到E+△E之间的微观状态数Ω(E)为
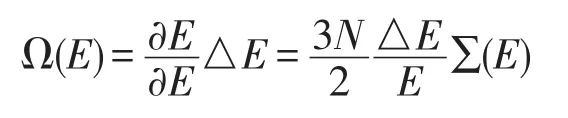
根据玻尔兹曼关系S=klnΩ,可得理想气体的熵为

由上式可解得
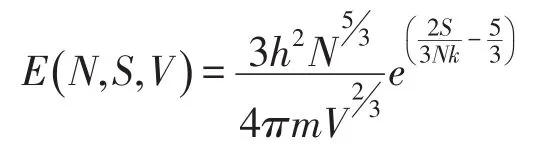
根据热力学基本方程dE=TdS-pdV
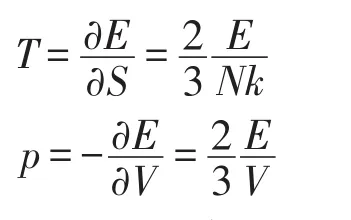
两式联立得状态方程为

3 用正则系综理论求
正则系综,把系统看作整体,系统能量不限制,其能量的表达式为

配分函数为
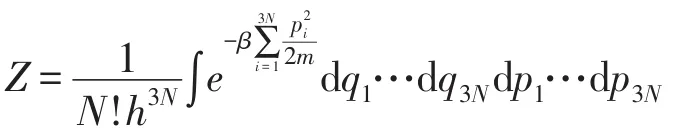
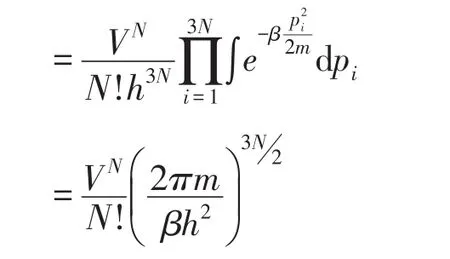
气体的方程为

4 用巨正则系综理论求
巨正则系综,把系统看作整体,其系统的粒子数和能量都能发生改变。求热力学函数须求出巨配分函数,其巨配分函数为

巨配分函数的对数为
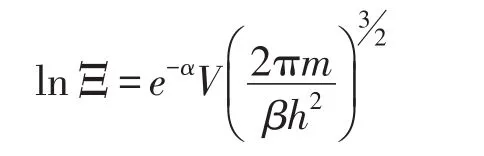
气体的平均粒子数为[2]
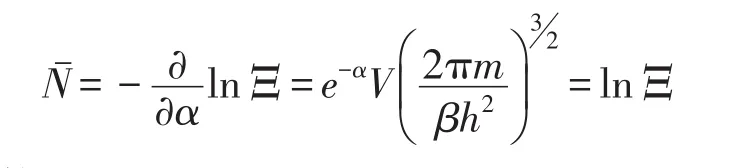
气体的压强为
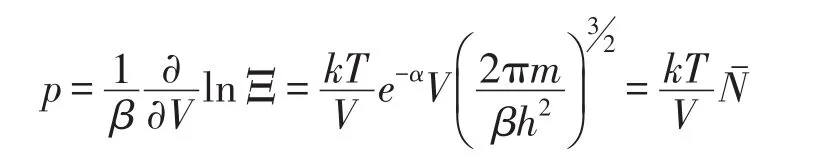
即理想气体的状态方程为

5 用麦克斯韦速度分布律求
用n=NV表示单位体积内的分子数,则气体处于平衡状态时,在单位体积内,速度在dvxdvydvz内的分子数为

上式即为麦克斯韦速度分布律[3]。
如图1所示,dA是器壁上的一个面积元,其法线方向沿x轴。以dΓdAdt表示在dt时间内,碰到dA面积上,速度在dvxdvydvz范围内的分子数。其分子数就是位于以dA为底,以v→(vx,vy,vz)为轴线,以vxdt为高的柱体内,速度在dvxdvydvz范围内的分子数。根据图1得


图1 分子碰撞
假设分子与器壁的碰撞为弹性碰撞,则这些分子给dA面的冲量为
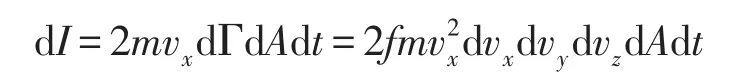
在dvxdvydvz范围内的分子,对器壁产生的压强为
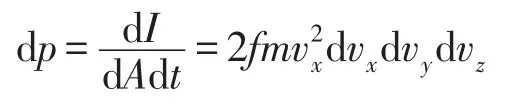
所有气体对器壁产生的总压强,就是对上式积分,
其中vx从0到∞,vy和vz从-∞到∞,即得

根据统计物理学常用的积分公式
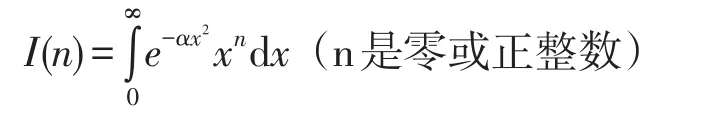
计算得出
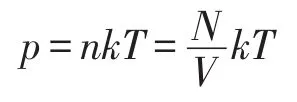
即理想气体的状态方程为

6 用位力定理求
假设热力学系统是由N个经典粒子组成,把系统看作一个整体,其自由度为3N。用H(q1,…,q3N;p1,…,p3N)表示系统的哈密顿量,根据正则分布,有

式中dω=dq1…dq3Ndp1…dp3N是相空间的体积元,xi或xj分别是6N个广义坐标和广义动量中的任意一个。令dω=dxjdω(j),dω(j)是除dxj之外其余6N-1个广义坐标和广义动量的微分。将上式改写为

并对其中的dxj进行分部积分,得
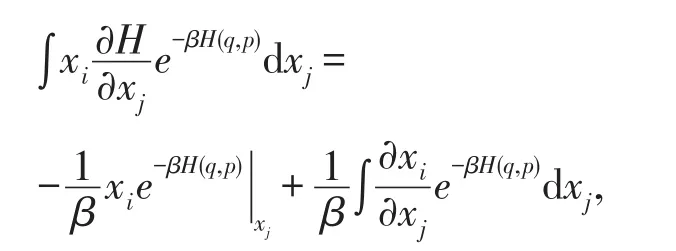
其中上面第一项要将xj的上下限代入。如果xj是系统的广义动量,将上下限±∞代入后H(q,p)趋于无穷,使第一项为零;如果xj是系统的广义坐标,其上下限是±∞或器壁坐标,代入后H(q,p)也趋于无穷,也使第一项为零。考虑到即有
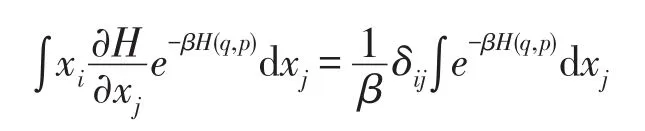
代入式(1)可得

式(2)称为广义能均分定理。
在广义能量均分定理中令xi=xj=qi,并利用正
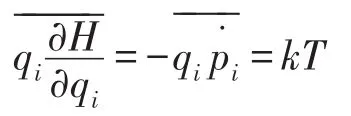
对i求和,i从1到3N,得
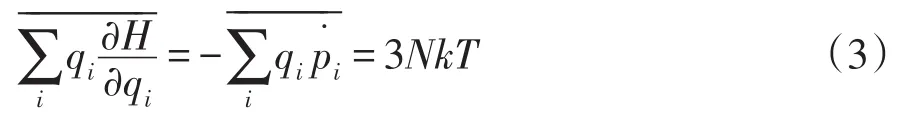

式(4)就是位力定理[3]。
对于单原子理想气体,分子间的相互作用可以忽略。所以上面的位力定理中的Fi是器壁对i自由度的作用力,则是器壁压力所产生的位力。以表示器壁面积元的外法线方向,p表示压强,面积元dA施于分子的力为
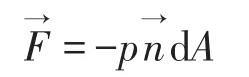
器壁压力产生的位力为

由于只有和器壁接近的分子才会受到器壁的作用力,(5)式中的是面积元dA附近分子的坐标,即面积元dA的坐标。(5)式的积分沿器壁的封闭面求积。根据数学的散度定理,可将面积分化为体积分

所以式(5)可写成

比较式(4)和式(6),即有
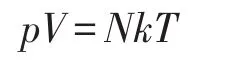
此式即为理想气体状态方程。
从上面的几种求解过程可发现,虽然求解方法不同,但结果是相同的,反映出统计物理的特点。
[1]吴瑞贤,章立源.热学研究[M].成都:四川大学出版社,1987.
[2]汪志诚.热力学·统计物理[M].北京:高等教育出版社,2012.
[3]冯玉广,李士.热力学与统计物理学导论[M].北京:中国科学技术出版社,2005.

