基于拟合与遍历的太阳影子定位研究

高彩云,胡国荣

（1.山西大同大学物理与电子科学学院,山西大同037009;2.吉林大学电子科学与工程学院,吉林长春130012）

目前常见的定位技术主要依靠卫星来实现，这种方法虽然精度高，但所需要的设备要求和技术要求也比较高[1-4]。太阳影子定位技术是通过分析物体的太阳影子变化，确定地点和日期的一种方法，这种方法简便易行，而且人工可操作性也比较强。我们都知道，物体的影长与物体本身的长度和太阳高度角有关，而太阳高度角又与太阳直射纬度、当地所在纬度和时角有关[5-8]。要想利用太阳影子确定地点和日期，就必须利用相应的数学和物理公式建立影长与杆长的数学模型，然后利用程序遍历所有可能的经纬度和日期，从而得到相应问题的解。

1 模型的建立

假设地球是一个标准的球体，忽略大气层对太阳光线的折射影响，杆与地面绝对的垂直。假设的变量及意义如表1所示。

表1 变量及意义说明

如图1所示，以地球上的一个位置作为研究的对象，以地球的球心为原点，地轴为z轴。并且以一个时间变量（该位置的当地时间t的变化来模拟地球的转动。x轴的选取方式为：当该位置位于xoz平面的第一卦限或第四卦限时，该位置为正午时刻，也就是说，x轴的位置是太阳光直射的经度位置。地球的自转方向为x轴正方向到y轴正方向。

图1 以地球的球心为原点建立的坐标系

用极坐标的方式来表示球面点的坐标，如图2，其中Ф为该点的纬度（∠AOB），R为地球的半径，β为角∠XOB的值（无特殊说明角度都为弧度制）。地球一小时内转过的角度为，且β为0时对应中午12时，所以

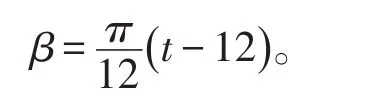
图2 极坐标表示球面点的坐标

对于光线的模拟只需要一个单位向量，由前面x轴的定义可知，该向量在XOZ平面内。设太阳光直射纬度值为α，查阅参考文献得α=23.45sin（n为从1月1日起经过的天数）[1]，则光 向 量(-cosα，0，-sinα)，点 A 的 坐 标 为（RcosФcosβ，RcosФsinβ，RsinФ），点A处切平面的法向量（即该位置垂直于地面向上的向量）为（cosФcosβ，cosФsinβ，sinФ）。

设γ与α的夹角为η，太阳高度角为δ，则可以推出下面的公式：

综上所述，所建数学模型为：

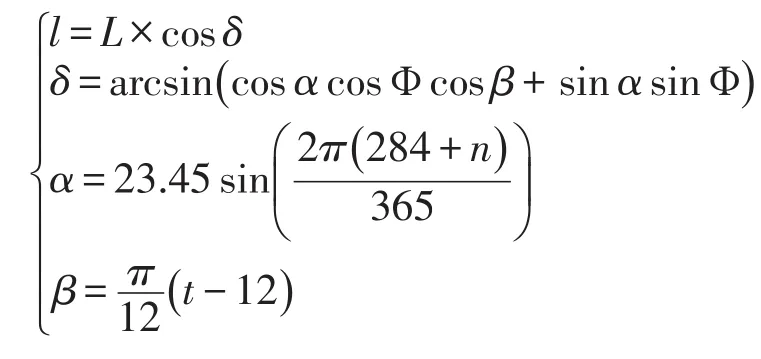
2 模型的算法实现

精密遍历：在初次遍历的结果的基础上，缩小纬度Ф，时差Δt，杆长L的遍历范围，增大遍历的密度，提高结果的精确度。

3 模型的运用

寻找一组可供使用的数据（源自2015年“高教社”杯全国大学生数学建模竞赛A题），时间与影长的关系表2所示。

3.1 春分到夏至

初次遍历，n:80～173(1)，Φ:-0.5*π～0.5*π(0.05*π)，Δt:-4.80～1.68(0.01)，L:0.5～3.0(0.01)，如表3所示。

精密遍历，n:120～125(1)Φ:0.62～0.63(0.001)，Δt:-3.00～-2.70(0.001)，L:1.50～2.00(0.001)，如表4所示。

得到日期n为122(5月2日)，纬度为0.627(N35°55′28′′),经度为E78°15′18′′。 根据太阳运动的对称性得夏至到秋分的日期为n=224(8月12日)。

3.2 秋分到冬至

初次遍历，n:266～356()1 ，Φ:0.5*π～0.5*π(0.05*π)，Δt:-4.80～ -1.68(0.01)，L:1～2.5（0.01），如表5所示。

精密遍历，n:302～307()1，Φ:-0.63～-0.62(0.001)，Δt:-2.90～ -2.70(0.001)，L:1.50～ 2.00(0.001),如表6所示。

得出日期n=305（11月2日），纬度为-0.629（S36°36′43′′）,经度为E78°18′54′′。根据太阳直射纬度变化的对称性得冬至到处分的日期n=42（2月11日）。

所得结果与数据出处近乎一致。

4 结语

本文建立了一个基于空间直角坐标系的模型，每一个坐标、向量简单明了，易于计算。在建立的过程中，由于充分考虑了当地时间与北京时间之间的关系，选择以本地时间而非本地经度作为模型的一个重要的变量，因而使模型化繁就简，易于理解。而且该模型与程序紧密相连，是通过程序来解决大量的数据，准确率也比较高。

由于在建模的过程中，我们忽略了大气对光的折射的影响，因而模型存在一些误差，在实际运用过程中，我们可以先计算出折射光线与原光线之间的夹角ɡ（实际上很小，因而被忽略），那么就可以计算出折射光线与地平面的夹角，由于折射光线与地面的交点和原光线与地面的交点距离较近（相对与地球半径），故可以用模型求出的太阳光线地球表面的夹角减去这个ɡ便得到了这个点的太阳高度角了。

表2 时间与影长

表3 春分到夏至初次遍历

表4 春分到夏至精密遍历

表5 秋分到冬至初次遍历

表6 秋分到冬至精密遍历

[1]方荣生.太阳能应用技术[M].北京：中国农业机械出版社，1985.

[2]黄玲,杨鹏辉,谢文,等.基于曲线拟合法太阳影子定位技术的研究[J].枣庄学院学报,2016,33(2):41-47.

[3]马玉雪,令狐林玉,杨东海,等.基于二次函数拟合的太阳影子定位技术研究[J].运城学院学报,2015(6):24-28.

[4]郑玉棒,张圣梅,汪婷,等.基于"穷举-非线性拟合"算法下的太阳影子定位分析[J].佳木斯大学学报(自然科学版),2015,33(6):832-836.

[5]黄小卉,朱家明,翁瑾,等.基于时空角度对太阳影子定位技术的研究[J].齐齐哈尔大学学报(自然科学版),2016(1):68-72.

[6]沈曙昀,王立,郭三敏,等.基于几何方法对太阳影子定位的研究[J].河北北方学院学报(自然科学版),2017,33(1):18-24.

[7]陈晓雪,汪劲希,王天钰.基于最优化模型的太阳影子定位方法[J].火力与指挥控制,2017,42(3):112-116.

[8]张志鹏,崔克楠,李厚彪.太阳影子定位的时空分析[J].实验科学与技术,2017,15(1):39-42.