盾构隧道下穿施工对邻近铁路桥梁的影响分析

孙雪兵

(中铁第四勘察设计院集团有限公司，湖北 武汉 430063)

近年来，随着城市轨道交通的大力发展，居民的出行得到了极大的便利。但由于城市轨道交通的建设通常受到城市空间的限制，将不可避免地出现盾构隧道穿越铁路桥梁等既有建(构)筑物的情况。地铁的穿越施工不但会引起周围地层损失从而导致地表沉降，同时也会造成既有桥梁结构出现不同程度的变形，从而给铁路线路的正常运营带来了潜在风险[1]。因此，新建盾构隧道与既有桥梁桩基的相对位置关系对控制结构的变形尤为重要。

国内学者对隧道下穿既有桥梁桩基展开了大量研究。王立峰[2]采用正交试验和数值模拟的方法，将盾构掘进过程中桩基与隧道间的距离进行分类，同时提出了桩基近邻度的计算方式；胡雄玉[3]采用有限元分析的方法，针对不同加固方式下盾构隧道施工对既有桩基的影响进行了研究；王述红等[4]以两阶段分析法为基础，考虑桩结构端承作用，对不同桩隧空间位置关系时盾构开挖对桩基的影响进行了研究，提出了盾构施工对桩基影响的理论计算方法。王俊[5]以长沙地铁盾构下穿新中路立交桥为工程依托，借助数值模拟分析了加固措施对控制桩基沉降的可行性；李旺旺等[6]以实际工程为例，通过地表沉降和桥桩监测数据，结合盾构土压力和注浆参数，研究了盾构侧穿桥梁时对桥梁沉降变形的影响；赵江涛等[7]建立盾构穿越既有桥梁的施工控制体系，并将之应用于东干渠盾构隧道穿越北苑桥主桥工程。朱逢斌等[8]通过建立三维有限元数值模型，对软土地区盾构掘进对邻近桩基的影响进行了研究，并通过离心试验验证了数值计算结果的可靠性；彭坤等[9]通过模拟盾构隧道顺桥向穿越桥梁桩基的全过程，对不同桩基加固方案下地表沉降和桩身变形规律进行了分析；夏炜洋等[10]采用数值计算的方法，针对盾构下穿万福桥时对桥梁结构的影响及管片衬砌结构的内力进行了分析；郑熹光[11]采用有限元法对不同工程地质、桩基形式和不同桩隧位置关系下桩体变形和受力进行了研究。

上述研究虽从多个角度对隧道穿越既有桥梁影响规律进行了分析，但是上述文献并未针对不同桩隧净距对地表及既有铁路桥梁结构的影响进行系统研究。为此，本文以武汉地铁3号线盾构隧道下穿既有铁路桥梁为工程依托，建立有限元数值模型，对盾构掘进过程中不同桩隧净距下盾构施工对既有铁路桥梁结构及地表的沉降规律进行研究，以期为类似工程提供参考。

1 工程概况

武汉地铁3号线一期工程二七路站—兴业路站区间盾构隧道先后穿越合武高铁、京广线等重要的既有铁路线路。隧道采用盾构法施工，衬砌结构外径6 m，内径5.4 m，幅宽1.5 m，厚0.3 m。新建盾构隧道与既有铁路桥梁位置关系见图1。

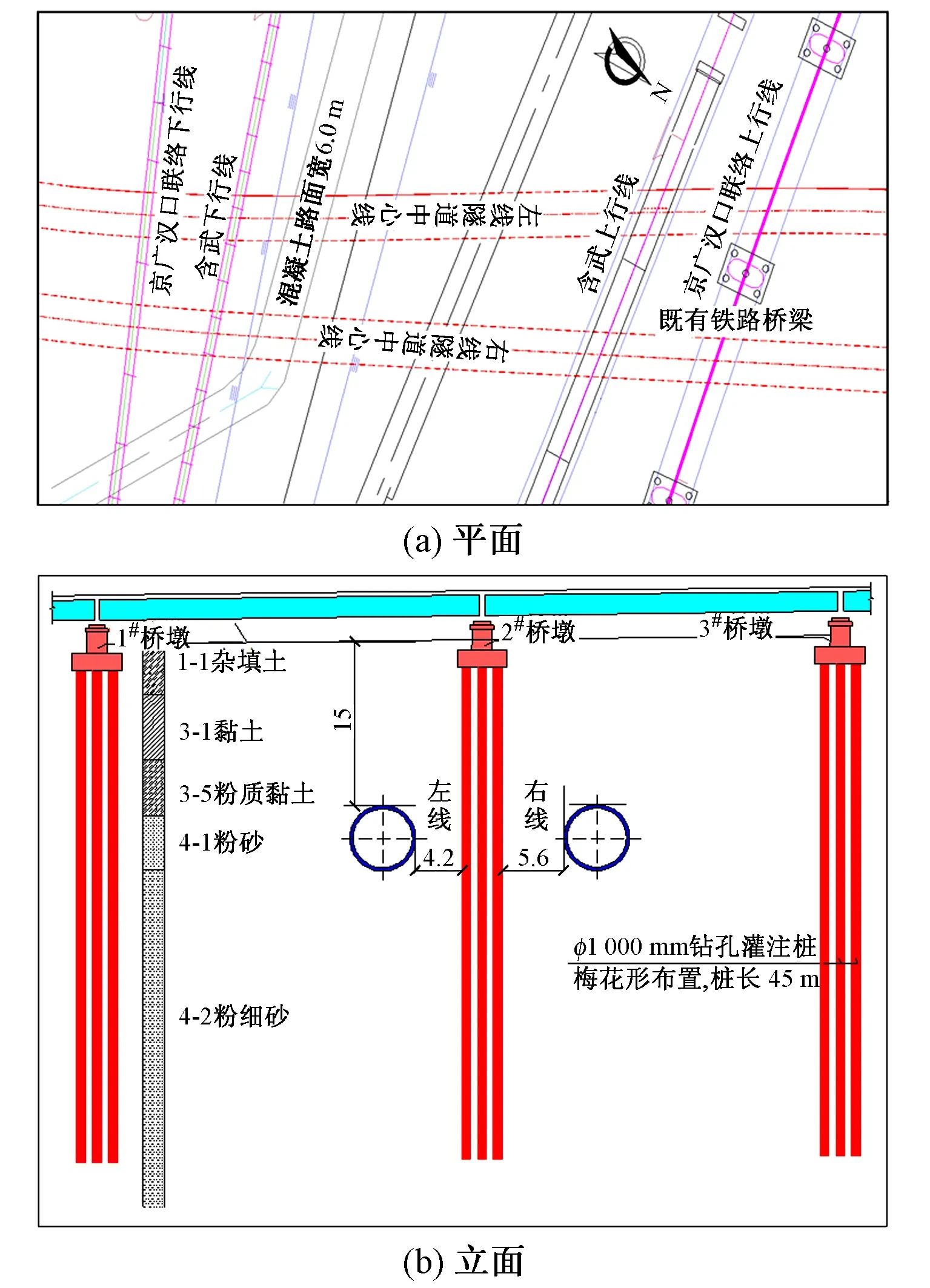
图1 隧道与既有铁路桥梁位置关系(单位：m)

2 盾构隧道下穿铁路桥梁数值模拟

2.1 模型的建立

计算模型中，土体、桥梁结构、管片和注浆层均采用Solid 45实体单元进行模拟，使用接触单元来模拟土体与桩基、梁体结构与桥墩之间的相互作用。考虑到隧道埋深较浅，在计算中对自重应力场进行处理。模型建立过程中对左右边界施加水平方向约束，模型底部施加竖向位移约束，顶部为自由面，前后边界施加纵向位移约束。

根据武汉轨道交通3号线与既有铁路桥梁桩基的位置关系，建立三维数值模型，见图2。

图2 三维数值模型

根据圣维南原理，模型范围取3～5倍洞径，沿隧道横向60 m，沿隧道纵向71 m，竖向土体厚度60 m。地层参数根据实际勘测资料取值，并假定不同地层均按照相应厚度水平层状分布。计算模型土体材料服从Druker-Prager准则，桥梁、墩台桩基等结构物则视为弹性体。

采用单元生死来模拟土体开挖、施作管片及注浆，通过调整注浆层参数的方法实现浆液的凝结硬化过程。同时，将隧道开挖引起的应力释放分为2部分，隧道开挖且未施作管片之前应力释放20%，在管片施作之后释放其余部分。双线隧道均设置12个开挖步，见表1。

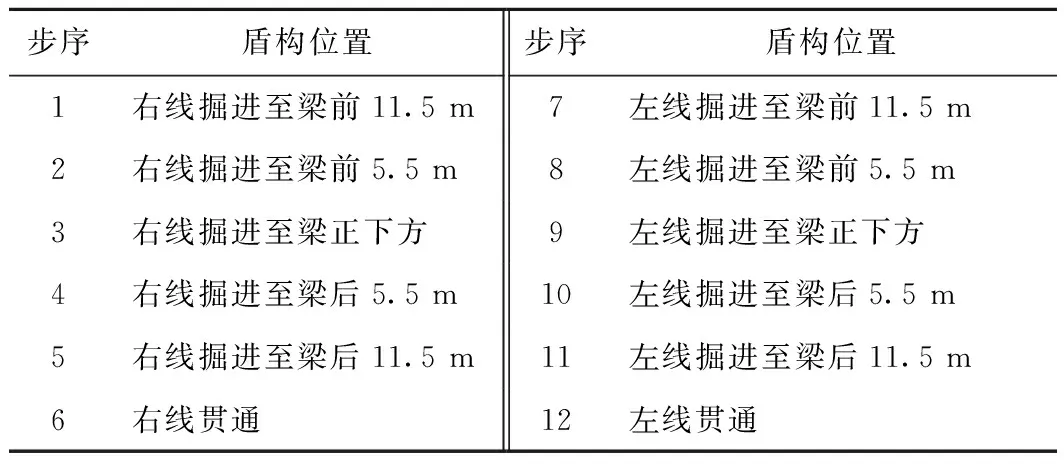
表1 开挖步情况

2.2 参数的选取

考虑到管片接头对结构刚度的影响，将结构刚度折减为0.85。同时结合地质勘查报告及相关规范确定岩土体及结构参数，见表2。

表2 岩土体及结构参数

2.3 结果分析

2.3.1 盾构掘进对地表及既有结构的影响

先开挖隧道右线，再开挖隧道左线。隧道埋深15 m，隧道左、右线与中间墩台桩基净距分别为4.2，5.6 m时既有桥梁中心线处地表沉降曲线见图3。

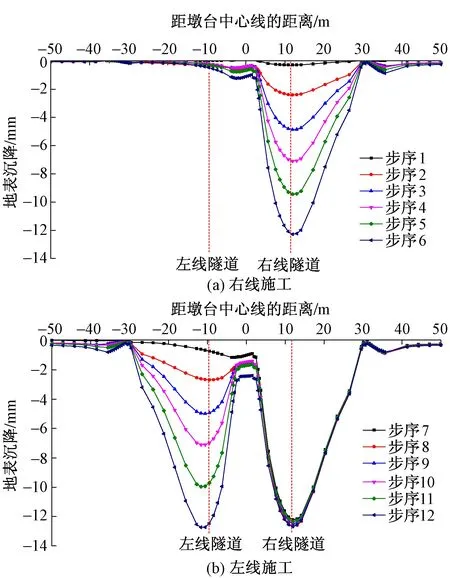
图3 地表沉降变化曲线

从图3可以看出：①开挖隧道右线时地表沉降呈V形分布，地表最大沉降区域在拱顶附近，且随着开挖的进行最大沉降呈增长趋势；②开挖隧道左线时地表沉降规律与右线基本一致，即随着开挖面的不断推进，地表沉降峰值逐渐增大；③双线贯通时隧道左右线中心处地表沉降最大值分别为12.737和12.678 mm，地表沉降呈W形分布。

右线贯通时隧道出口处沉降最大，其值为17.647 mm，双线贯通时地表沉降基本沿隧道轴线左右对称，最大沉降位于左线隧道出口，其值为20.374 mm。2#墩台周边地表沉降相对较小，表明桥梁桩基对其周围地层沉降有一定的抑制作用。墩台处与隧道进出口处的地表沉降差值为7.637 mm。

为获得盾构施工对既有桥梁桩基的影响，以2号墩台下部桩群为例进行桩基的位移分析。2#墩台桩基编号见图4。

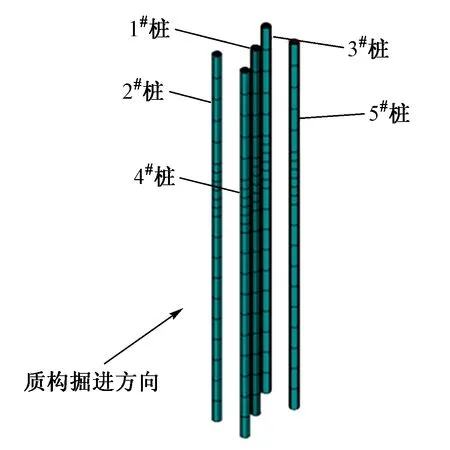
图4 2#墩台桩基编号

右线贯通时由于开挖中的地层扰动以及桥梁结构荷载的直接作用，桩群最大竖向位移出现在靠近右线的桩顶，其值为-1.347 mm。双线贯通时桩群的最大竖向位移靠近左线桩顶，其值为-2.649 mm，相较于右线贯通时有较大增长。桩群的上下两部分竖向位移存在着较大差异。上半部分桩基位于隧道施工影响线之内，下沉量较大。下半部分桩基由于受到的施工扰动较小，且该部分地质条件相对较好，下沉量较小。

隧道双线贯通时2#墩台下部桩群垂直于盾构掘进方向(X方向)的水平位移见图5。水平位移以远离左线隧道的方向为正向，反之为负向。

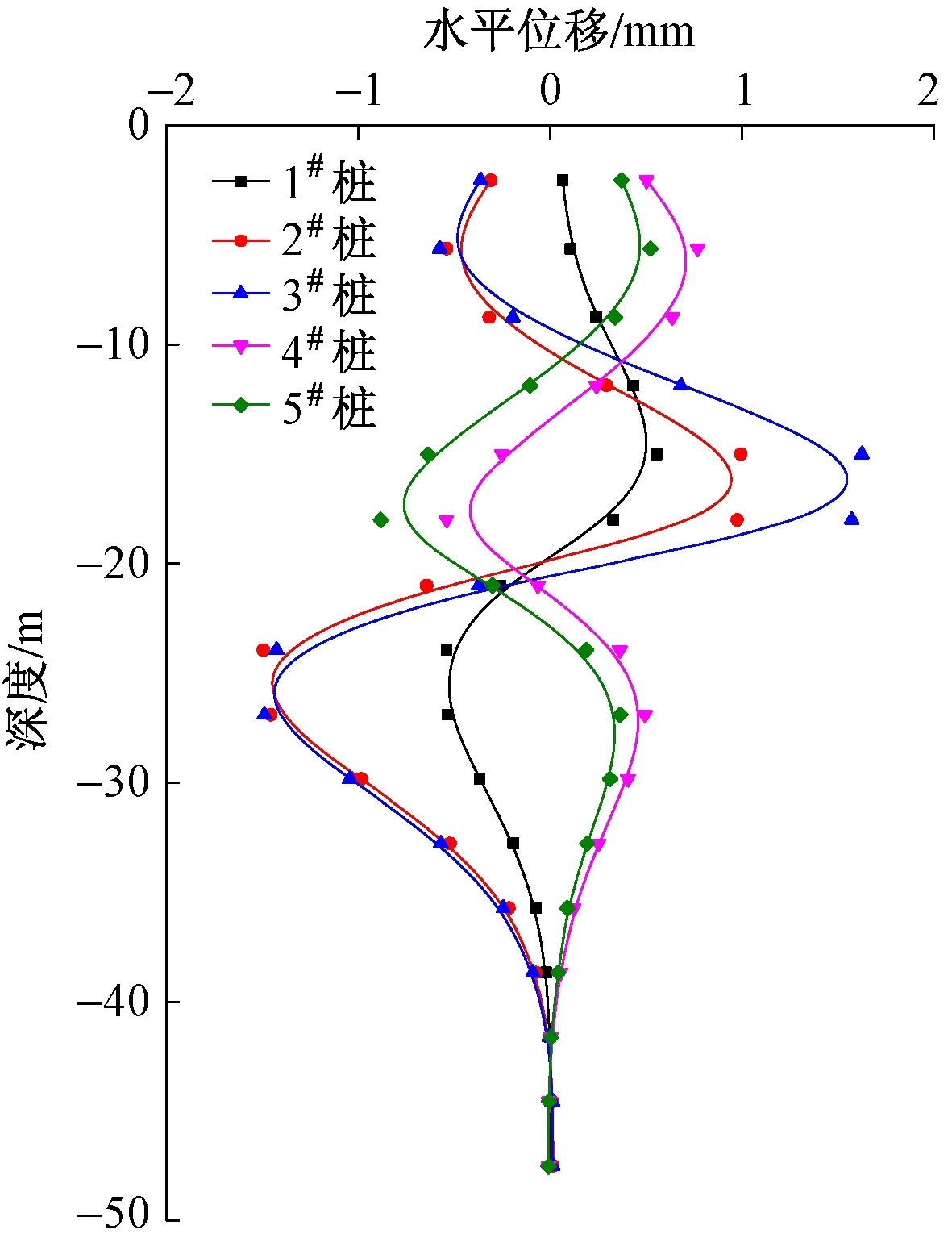
图5 2号墩台下部桩群水平位移曲线

从图5可以看出：①1#桩位于墩台中心处，由于其与左线隧道距离较近，故其在隧道中心处出现了正向位移，在深度25 m处出现了负向位移，最大水平位移为0.556 mm，但位移小于其他4根桩基。②2#，3#桩位移变化规律与1#桩相一致，正向最大水平位移分别为0.995，1.626 mm。这是由于2#，3#桩距左线更近，因此水平位移相对较大。③4#，5#桩位移变化规律与2，3#桩相反且量值相对较小，4#，5#桩最大水平位移分别为-0.538，-0.882 mm。

2.3.2 桩隧净距对地表及既有结构的影响

在隧道埋深、右线隧道与既有桥梁桩基距离一定的情况下，隧道左线与2#桩基之间的桩隧净距分别取1.8 m(0.3D)，4.2 m(0.7D)及6.0 m(1D)。D为隧道外径，其值为6 m。双线贯通时地表沉降变化曲线见图6。图中虚线为不同工况下的隧道中心线。

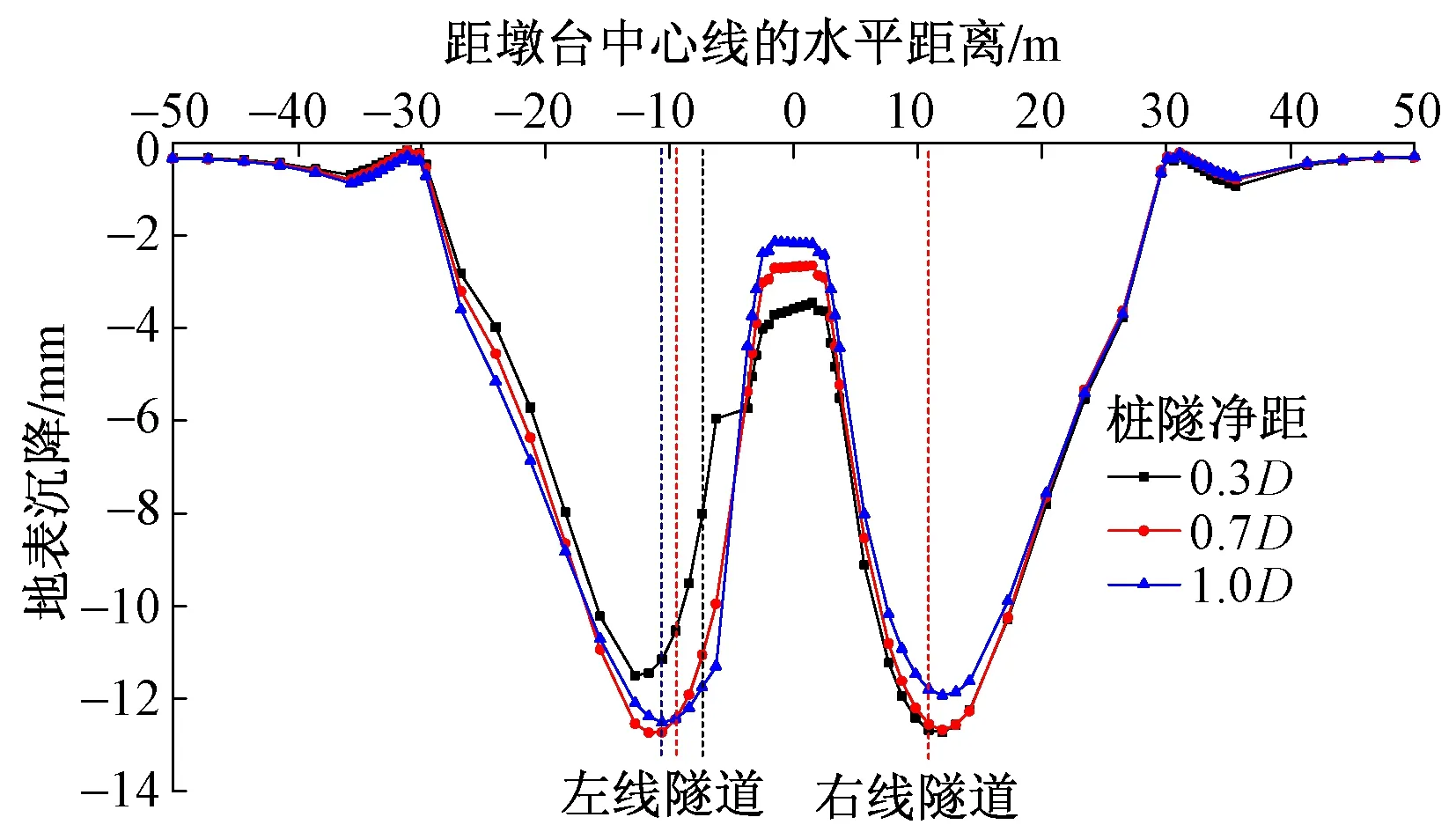
图6 双线贯通时地表沉降变化曲线

从图6可以看到：①桩隧净距分别为1.8，4.2及6 m 时地表沉降均呈W形，且随着桩隧净距的增大,地表沉降最大值分别为12.729，12.737及12.515 mm;②墩台及右线隧道中心线附近的地表沉降随着桩隧净距的增大而减小。这是由于左线隧道的开挖对墩台处地层的扰动逐渐减小。

不同桩隧净距下梁体结构最大位移见表3。

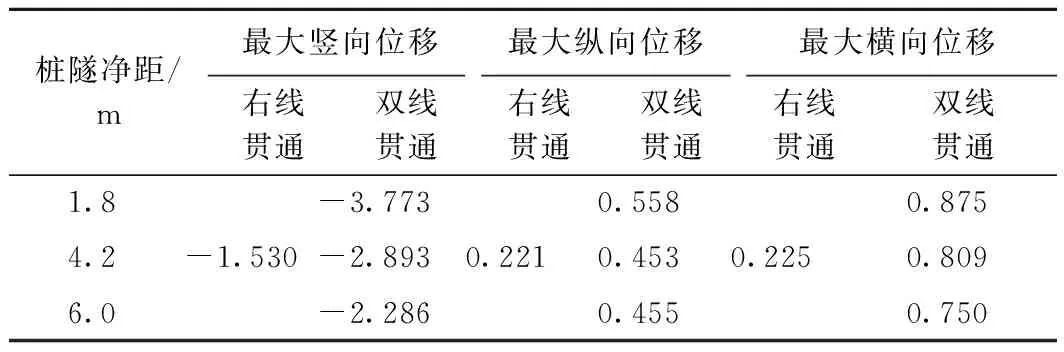
表3 不同桩隧净距下梁体结构最大位移 mm

从表3可知：①由于首先对右线隧道进行开挖，右线贯通时左线还未施工，故在不同桩隧净距下梁体结构最大位移相一致。②双线贯通当桩隧净距由1.8 m 增至6.0 m时，梁体结构最大竖向位移由-3.773 mm逐渐减小至-2.286 mm，最大沉降点均在2#墩台顶。同时，随着桩隧净距的增大梁体结构水平位移有所减小，但变化幅度很小，均不足1 mm。③不同桩隧净距下梁体结构产生的变形以竖向位移为主。

双线贯通时钢轨竖向位移变化曲线见图7。可知：2条钢轨沉降变化规律基本一致，钢轨竖向位移基本呈V形，轨道各点的沉降均随着桩隧净距的增大而减小。

图7 双线贯通时钢轨竖向位移变化曲线

不同桩隧净距下钢轨最大竖向位移及位置见表4。可以看出：桩隧净距的增大对钢轨沉降的影响并不明显，不同桩隧净距下钢轨最大变形处钢轨高差均不足0.1 mm，且最大竖向位移未超过6 mm的限值。

表4 不同桩隧净距下钢轨最大竖向位移及位置 mm

桩基最大竖向位移见表5。可见：随着桩隧净距的增大，桩基最大竖向位移呈减小的趋势。桩隧净距为1.8 m时桩基最大竖向位移为-3.998 mm，桩隧净距分别增至4.2，6.0 m时桩基最大竖向位移分别为-2.954，-2.309 mm，表明隧道开挖对桩基竖向位移的影响随着桩隧净距的增大而减小。

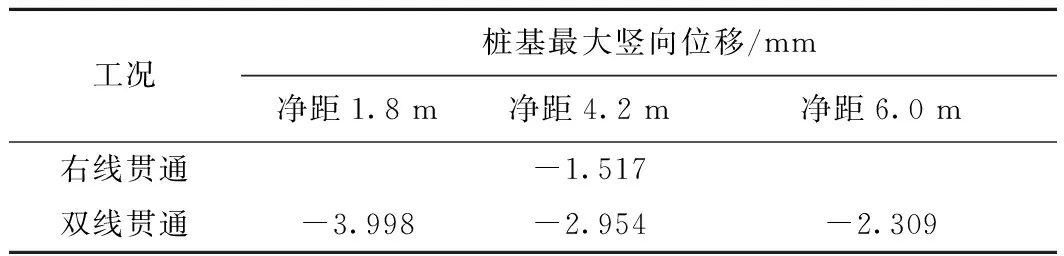
表5 不同桩隧净距下桩基最大竖向位移

由于2#桩、3#桩与隧道左线的距离较近，故选取2#桩作为桩基水平位移的监测对象。双线贯通时2#桩垂直于盾构掘进方向(X方向)的水平位移曲线见图8。

图8 双线贯通时2#桩水平位移曲线

由图8可见：①由于左线隧道开挖对土体产生扰动，在隧道中心处2#桩正向水平位移达到最大值，桩隧净距为1.8，4.2和6.0 m时2#桩在隧道中心处的水平位移分别为1.996，1.204，0.738 mm；②在隧道中心以下约8 m处2#桩负向水平位移达到最大值，3种净距下其值分别为3.413，1.594及0.867 mm；③随着桩隧净距的增大，2#桩水平位移明显减小，这表明隧道开挖对2#桩水平位移的影响会随着隧桩净距的增大而减小。

3 结论

1)盾构隧道的掘进会使邻近桩基产生以沉降为主的附加变形，其最大沉降发生在桩顶；随盾构的推进地表沉降表现出较为明显的增长趋势，至隧道双线贯通时地表最大沉降值为20.374 mm。

2)既有桥梁桩基对盾构开挖引起的地层扰动能起到一定的阻隔作用，从而减小了盾构施工所引起的变形。同时，由于桩侧摩阻力的作用，2#墩台周围的地表沉降最大值小于隧道进出口处。

3)在桩隧净距分别为1.8，4.2，6.0 m时，桥梁梁体与桩基产生的变形均以沉降为主，变形量随桩隧净距的增大而减小。随桩隧净距的增大相邻两股钢轨水平高差及轨面沉降的变化趋势不明显，均未超出6 mm的限值。

[1]王霆,韩高孝,郑军.盾构下穿施工对高铁连续梁桥沉降和变形的影响[J].城市轨道交通研究,2016,19(4):38-41.

[2]王立峰.盾构施工对桩基的影响及桩基近邻度划分[J].岩土力学,2014,35(增2):319-324.

[3]胡雄玉.不同加固方式下盾构施工对桥梁桩基影响的研究[J].铁道建筑,2013,53(3):75-77.

[4]王述红,赵贺兴,姜磊,等.基于两阶段法地铁盾构开挖对邻近桩基影响分析[J].东北大学学报(自然科学版),2014，35(6):871-874.

[5]王俊.旋喷桩与袖阀管注浆在桥梁桩基加固中的应用[J].铁道建筑,2013,53(9):24-26.

[6]李旺旺,韦宏鹄.北京昌平线二期地铁盾构侧穿桥梁沉降监测分析[J].隧道建设,2015，35(2):139-143.

[7]赵江涛,牛晓凯,崔晓青,等.盾构隧道下穿既有桥梁精细化施工控制[J].铁道建筑,2017,57(10):63-66，77.

[8]朱逢斌,杨平,ONG C W.盾构隧道开挖对邻近桩基影响数值分析[J].岩土工程学报,2008,30(2):298-302.

[9]彭坤,陶连金,高玉春,等.盾构隧道下穿桥梁引起桩基变位的数值分析[J].地下空间与工程学报,2012,8(6):485-489.

[10]夏炜洋,何川,葛蔚敏,等.成都地铁一号线盾构机下穿万福桥数值模拟分析[J].铁道建筑,2009,49(4):46-48.

[11]郑熹光.盾构隧道施工对邻近桩基础位移和受力特性的影响研究[D].北京:北京交通大学,2015.