亲历探究过程 丰富知识体验
———实践活动课《年历里的秘密》教学实录
周道鑫(特级教师)

【教学内容】
苏教版三年级下册第44、45页。
【教学背景】
教学三年级《年、月、日》单元时,发现苏教版教材在编排“认识年、月、日”和“认识平年、闰年”都是通过年历来帮助学生学习的,教学结束后发现学生掌握的知识都是机械式、碎片化的,对年、月、日的知识缺乏一个体验的过程和深刻的理解。为此,特开发出本节实践活动课——《年历里的秘密》。以期让学生亲历探究过程,丰富知识体验。
【教学过程】
一、谈话导入
师:今天是个特别的日子,因为我和大家将学习一节特别的数学课——综合实践课。什么是综合实践课?顾名思义,就是综合运用多种知识,解决相关实际问题,重点培养大家发现问题、提出问题、分析问题和解决问题的能力。大家有信心一起来学好这节课吗?
师:说到今天,到底是个什么日子?我们刚学习年、月、日,谁能像这样给大家介绍一下:今天是(2017)年(5)月(17)日星期(三)。那昨天呢?(昨天是2017年5月16日星期二)明天呢?(5月18日星期四)后天呢?(5月19日星期五)一年中随意哪一天都能这样张口就来介绍吗?(不能)但如果我们有了一样宝贝,就能轻松做到,猜猜是什么宝贝?(年历)
二、欣赏年历
师:年历是什么样的?最近我们班的同学学过《年、月、日》后,都亲手制作了一张年历。想看看吗?(想)那好,就让我们一起来静静欣赏……
师:看到这些年历,你有什么想说的?
生:制作精美、漂亮,也想亲手制作一张年历。
师:想做,但做年历也不是件很容易的事。不过,在班级年历评比分享会上,我们班一位同学骄傲地说了这样一句话“只要告诉我某一天是几月几日星期几,我就能制作出这一年的年历”。
师:一年365天,只要知道其中一天就可以制作出一年的年历。是真是假?特别是他还用了一个关联词语“只要……就……”,好像很有把握似的,特别骄傲。这让老师想到著名科学家阿基米德也说过一句类似的、更骄傲的话:只要给我一个支点,我就能撬动地球。
师:科学家撬动地球需要一个支点,这位同学制作年历需要知道一年中其中一天是几月几日星期几。你们认为有道理吗?实践是检验真理的最好办法!我们动手试试吧!
三、动手操作
1.制作月历。
师:拿出空白年历卡,观察一下,你有什么发现?
生:一年有12个月。
生:每个月的第一行都是周日、周一、周二……周六的排列。
师:也就是年历卡上一周从周日开始到周六结束。
师:那就从今天开始,请你试着完成5月的月历。
(学生自主填表)
师:谁来汇报一下,你是怎么填的?
生:知道了今天是5月17日星期三,就能知道明天是5月18日星期四;知道了明天,就能知道后天是5月19日星期五,知道了后天,就能知道下一天,这样一天一天往下填。
师:他的意思是知道今天是5月17日星期三,就能知道明天,从明天又能想到明天的明天,这样一直可以往后写下去。还有不一样的想法吗?
生:知道了今天是5月17日星期三,就能想到昨天是5月16日星期二;再根据昨天,就能想到前天是5月15日星期一,这样倒着排就能填出5月前面的月历。
师:两位同学的想法都和哪一天有关?
生:今天,5月17日星期三。根据今天往后推,就能推出后面的月历,往前推就能推出前面的月历,合起来就是5月完整的月历。
师:简单地说,就是由今天往后想,想到明天;往前想,想到昨天。这样一天一天往后想、一天一天往前想,就把一个月的日历都想出来了,这其实就是一种推理,或叫做推想。
2.制作年历。
师:知道一天我们可以完成一个月的月历制作,可离一年12个月的月历还差老远呢!我们又怎么推想才能推想出一年的年历呢?小组内互相讨论讨论,并试试看是否可行?
师:哪一组来汇报一下你们的想法和做法?
组1:根据5月最后一天是5月31日星期三,就能推出6月的第一天是6月1日星期四,知道了这一天,就能制作出6月的月历。再根据6月的最后一天就能推算出7月的第一天,也就能完成7月的月历,就这样一个月一个月地推下去,就能完成后面的月历。
师:根据5月的最后一天,推算出后面几个月的月历,那5月前面的月历怎么推算出来呢?
组2:根据5月的第一天是5月1日星期一,可以推算出4月的最后一天是4月30日星期日,往前倒着推就能推算出4月的月历。同样的,根据4月的第一天推算出3月最后一天,就能完成3月的月历,一个月一个月地倒着推,就能推出5月前面的月历。
师:看来根据5月的最后一天往后推,就能推算出5月后面的月历;根据5月的第一天往前推,就能推算出5月前面的月历。这个过程与5月的月历推想过程极为相似,现在按这种推法只往前、往后推算一个月,就是6月和4月,试试能否成功?
师:你们成功了吗?(成功了)看来我们的推想经检验是合理的,照此推想下去,我们是能够把一年12个月的月历全部完成的,只是课堂上时间有限,剩下的请大家课后完成,比一比,谁做的更精美、更漂亮。
3.感受体验。
师:现在回过头想想“制作年历需要知道其中一天是几月几日星期几”这句话是真是假?(真的)2017年的年历完成了,能否完成2018年和2016年的年历呢?
生:能!根据2017年的最后一天和第一天,就能知道2018年的第一天和2016年的最后一天,知道了其中一天,就能制作出这一年的年历了。
师:说得真好,那就让我们再一起读一遍那句话:只要告诉我某一天是几月几日星期几,我就能制作出这一年的年历。
四、研究年历
1.合作探究。
师:我们学会了制作年历,还要仔细研究年历,也许其中蕴藏着许多秘密等待大家去发现。请同学们仔细观察5月的月历,四人小组共同研究他们的日期排列,看看能有多少不同的发现?
……
2.分组交流。
生:我们横着看,后一个数都比前一个数大1。
师:我们看看是不是这样(电脑验证),果然是,为什么会相差1呢?
生:今天的日期比昨天大1,明天肯定也比今天的日期大1。
师:很浅显的道理,横着看(→)相差1。还有不一样的发现吗?
生:还可以竖着看,下面的数比上面大7。
师:是这样吗?竖着选几组来验证一下。
师:竖着看(↓),为什么会相差7呢?
生:竖着看,比如 3、10、17、24、31,这一组都是星期三,上一个星期三到下一个星期三,正好相差一个星期,也就相差7。
师:真棒!这位同学能够举例来说明竖着看为什么相差7。星期四这一组有这样的规律吗?星期五、星期六呢?……你能用一句话来说明为什么相差7吗?
生:竖着看,两个日期正好相差一周,一周是7天,所以相差7。
师:可以横着看、竖着看,还可以怎么看?
生:还可以斜着看。
师:怎么斜看着?能否也举个例子?
生:1、9、17、25。(根据学生回答圈出这组数)
师:这种斜的方向是(右下),那我们就称之为右下斜(↘),它们有什么规律?
生:相邻两个数相差8。
师:相差8,这里又有什么奥秘呢?
生:1日是星期一,9日是下个星期二,与1日比差一星期还多一天,就是相差8天。
生:17日是星期三,和上周的星期二(9日)比,差一个星期还多一天,就是7+1=8天。
师:再换一组看看是否也是这样……
师:右下斜,两个数相差8。如果反过来左下斜(↙),两个数相差多少?
生:相差6,两个日期相差一个星期少一天,就是6天。
师:我们也通过几组数来验证一下……果然如此,左下斜,两个数相差6。
3.感受策略。
师:刚才我们从不同的角度来观察,发现日期有不同的排列规律。这些规律我们是用什么方法发现的?
生:通过举例子的方法。
师:通过一个例子就行吗?
生:不行,还要举好几个例子来验证。
师:也就是说发现规律后必须进行验证,其实刚才大家不知不觉就使用了科学研究的一般方法:发现问题——提出猜想——举例验证,验证正确后,一般还有关键的一步,就是解决问题。如果用刚刚发现的规律来解决一些实际问题,敢挑战吗?(敢)
五、解决问题
1.研究三个日期之和。
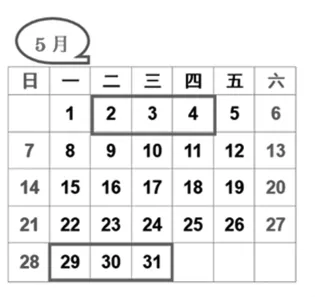
小明家计划5月份外出旅游3天,小明看了月历,计算一下三个日期之和,正好是9。你知道小明家准备哪三天出去旅游吗?
师:这时我们需要(5月的月历),三个日期之和是9,究竟是哪三天呢?
生:2、3、4 三天。
生:直接用 9÷3=3,所以就是2、3、4 三天。
师:首先我们验证一下这三天是否符合题意?(符合,相加的和是9)谁明白刚才那位同学的发言?
生:用 9÷3=3,就说明中间的日期是5月3日,三天就是2日、3日、4日这三天。
生:2、3、4,4 借 1 给 2,就变成3、3、3。三个日期都变成3了,三三得九,说明三个数的和是中间日期的3倍。
师:是这样吗?这仅仅是我们的猜想,还需要进行验证,是不是在月历上任意框出三个数,都存在这样的规律呢?请拿出研究单对照月历框一框,看看你有什么发现?
……
师:通过研究单,我们发现不管怎么框,三个日期数都可以变成同一个数,我们就可以用一个数量关系式表示和与中间日期数的关系。
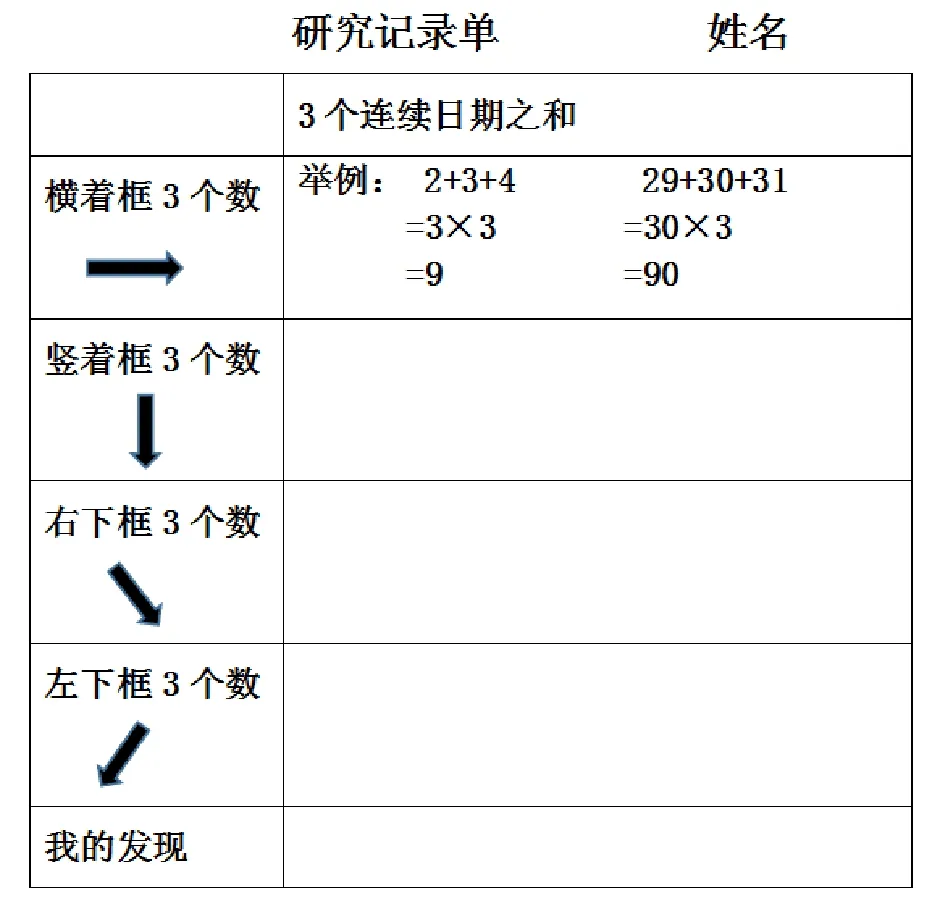
?
生:和÷3=中间日期数。
生:还可以用:中间日期数×3=三个日期的和。
2.研究五个日期之和。
师:横着框、竖着框,组成一个“十”字形,用它可以框出五个数,你能快速算出五个数的和吗?
生:中间的数乘5。
生:下面的数借7给上面的数,右面的数借1给左边的数,这样5个数都变成中间的数,所以用中间数乘5。
师:看来五个日期的和也可以用一个数量关系式来表示:中间日期数×5=五个日期的和。
3.研究九个日期之和。
师:如果把“十字形”的四角补上,就变成了“九宫格”,要填出这九个数,你最想知道哪个数?
生:中间的数。
生:知道中间的数,就可以推算出四周的8个数。
师:猜猜这九个数的和又怎么快速来计算?
生:中间日期数×9=九个日期的和。
六、总结设疑
师:同学们,我们一节课都是在研究年历,通过这节课的学习,你有什么收获?
生:学会了制作年历。
生:发现了年历里的日期排列的许多规律。
生:学会了快速计算年历里几个日期之和。
师:其实,大家不仅学会了前面所说的一些数学知识,更重要的是亲身经历了科学研究的一般过程,掌握了科学研究的一般方法(发现问题——提出猜想——验证猜想——解决问题),特别是在解决问题的过程中又发现了3个日期、5个日期、9个日期之和的计算方法,它们可以用一个数量关系式表示:中间日期数×个数=日期的和。
师:不过同学们有没有想过,如果没有中间日期数,像这样框出的四个日期数,他们的和又有什么样的规律,请大家课后继续探索。


