基于HP滤波法的新疆枣果价格波动特征

刘妮雅，王慧军

(1.河北农业大学，河北保定 071051；2.河北金融学院，河北保定 071051；3.河北省农林科学院，河北石家庄 050051)

0 引 言

【研究意义】新疆枣产区具有日照时间长、降水量少、土壤肥沃、病虫害较少等得天独厚的气候条件和栽培优势，其枣树栽培面积和产量逐年扩大，面积由1999年的4 258 hm2提高到2016年的504 511 hm2，总产量由1999年的6 158 t提高到2016年的3 264 167 t。新疆林果产业发展规模逐年扩大，截至2016年，新疆各类水果及坚果种植面积达到993 758 hm2，其中，枣树种植面积约占50.77%；新疆占全国枣产量的比例近40%，其市场占有率更高达70%以上，枣产业已经成为新疆农业的新型主导产业。新疆枣果价格的变动对全国枣果市场的变动起着决定性作用。近年来，新疆枣价出现下滑，年际间、月季间波动频繁。研究新疆枣价的波动特征和规律，为调节价格波动幅度、促进枣产业发展提供参考。【前人研究进展】Census X-12季节调整法[1]是在X-11季节调整法的基础上发展而来的，该方法可将季节变动要素和不规则变动要素从时间序列数据中剔除，更客观反映时间序列数据的经济变化规律[2]；HP滤波法最初由Hodrick& Prescott(1980)提出，是时间序列在状态空间的分解方法，HP滤波法被应用于分析农业经济、房地产和证券市场等领域。胡友等[3]将HP滤波法应用于我国水果价格长期波动趋势和短期波动周期的分析，认为水果价格具有稳定上涨的长期趋势，部分因素会使价格出现短期剧烈波动；周霞等[4]运用HP滤波模型分析山东苹果产业各环节的价格波动特征，认为生产成本和支农政策对价格波动影响最大；贾小玲等[5]采用HP滤波法和ARCH类模型研究大麦波动价格特征及其影响，有助于提升大麦产业链主体识别和应对市场风险能力；黎东升等[6]采用HP和BP滤波法对比分析生猪价格的波动特征，2008年前后生猪价格周期波动差异显著。Census X-12季节调整法和HP滤波法在分析农产品市场价格中得到较为广泛应用。【本研究切入点】目前，尚未有文献就枣的市场价格波动趋势和特征进行研究。研究选取2010年4月至2017年5月间新疆枣果的市场价格数据，采用Census X-12季节调整法和HP滤波法分析价格变动趋势、波动规律和波动特征，以及新疆枣产业发展和供给特点对市场价格产生的影响。【拟解决的关键问题】分析新疆枣果的价格变化特征，研究价格波动规律，为枣农和相关企业生产提供参考。

1 材料与方法

1.1 材 料

收集中国枣网(http://www.cnzao.com)2010年4月至2017年5月间全国各地批发市场中新疆枣的市场价格，以月度时间序列数据作为研究对象，如果月度价格数据多于1个，则取多个数据的平均值作为当月价格。

1.2 方 法

采用HP滤波法研究新疆枣价的波动规律和波动特征。采用CensusX-12季节调整法对新疆枣果价格数据进行预先处理，获取价格波动的长期趋势；在此基础上，通过HP滤波法分析价格波动规律和波动特征，数据分析过程采用的软件分别为SPSS22.0和Eviews8.0。

1.2.1 季节调整法

采用季节调整法预先分析处理新疆枣价的月度数据。季节调整法认为时间序列包含4种变动因素：长期趋势变动T(Trend)、季节性变动S(Seasonal Fluctuation)、周期性变动P(Periodicity)和不规则波动性I(Irregular Variations)[7]，月度时间序列可分解为T、S、P、I之和，Yt=Tt+St+Pt+It。其中，

长期趋势T：表示随着时间的推移，数据随之逐渐增加、减少或者不变的长期发展趋势。

季节趋势S：表示由于受到季节因素的影响或某些习俗的影响，数据出现有规律变化的规则。

周期性趋势P：表示数据取值沿着趋势线有如钟摆般循环变动的规律。

不规则趋势I：表示把时间序列中的长期趋势、季节趋势和周期性趋势都去除后剩下的部分。在分析新疆枣价的波动特征时需要对时间序列数据进行分解，去掉季节波动性的影响，即所谓的“季节调整”(Seasonal Adjustment)。Census X-12是基于移动平均法的季节调整法，它可以把时间序列Y中的随机成分I和季节成分S分解出来，剔除时间序列数据中季节变动要素和不规则变动要素，对时间序列中各变动因素之间的关系，通常有加法关系假设和乘法关系假设，相应的采用时间序列季节分析的加法模型和乘法模型。

加法模型：假设各成分之间彼此独立，没有交互影响，时间序列是由长期趋势性、季节性、周期性和不规则性迭加形成的。如果以Y表示某个时间序列数据，加法模型即为Y=T+S+P+I。加法模型中的季节性因素、周期性因素和不规则性因素都围绕长期趋势而上下波动，反映了各自对时间序列的影响方式和程度。加法模型一般适用于随着时间推移，波动幅度没有明显变化的时间序列。

乘法模型：假设各成分之间是相互依赖的，时间序列是由长期趋势性、季节性、周期性和不规则性相乘形成的。如果以Y表示某个时间序列数据，乘法模型即为Y=T×S×P×I。乘法模型中的季节性因素、周期性因素和不规则性因素也是围绕长期趋势而上下波动，反映了各因素在长期趋势的基础上对原始时间序列数据的相对影响方式和程度。乘法模型一般适用于随时间推移，波动幅度随之增大或减小的时间序列。

Census X-12季节调整法的核心算法分为三个阶段：

第一阶段，季节调整的初始估计。

(1)TPt表示时间序列的趋势循环成分，通过中心化12项移动计算平均趋势循环成分的初步估计，

TPt=(0.5yt-6+yt-5…+yt+5+0.5yt+6)/12.

(2)计算SI项的初始估计，

SIt=Yt-TPt.

(3)通过3×3移动平均计算季节成分S的初始估计，

(4)消除季节成分中的残余趋势，

(5)季节调整结果的初始估计，

TPIt=Yt-St.

第二阶段，计算暂定的趋势循环成分和最终的季节成分。

(1)利用Henderson移动平均公式计算暂定趋势循环成分，

(2)计算暂定的SI项，

SI't=Yt-TP't.

(3)通过3×5项移动平均计算暂定的季节成分，

(4)计算最终的季节成分，

(5)季节调整的第二次估计结果，

TPI't=Yt-S't.

第三阶段，计算最终的趋势成分和最终的随机成分

(1)利用Henderson移动平均公式计算最终的趋势循环成分，

(2)计算最终的随机成分，

I"t=TPI't-TP"t.

在Census X-12季节调整法中，趋势成分和周期性成分被视为不可分开的整体，时间序列Yt的趋势循环成分TPt包括了趋势成分和周期性成分。

1.2.2 HP滤波法

经过CensusX-12季节调整后的数据反映出趋势循环变动成分TPt，采用HP滤波方法剔除掉趋势变动成分，得到循环周期成分。HP滤波法通过设计一个近似的高通滤波器(High-Pass Filter)，在不同频率的成分中分离出较高频率的成分(中短期波动)和较低频率的成分(长期趋势)，也就是将变化不定的时间序列数据中具有一定趋势变化的平滑序列分离出来，将时间序列数据分解为平稳变化的趋势性成分和周期波动性成分。HP滤波法假设时间序列数据为Yt(t=1,2,...,T)，Yt由趋势性部分Tt、周期波动性部分Pt和误差项εt组成，即

Yt=Tt+Pt+εt.

HP滤波法的具体计算方法为使下面的损失函数最小，即

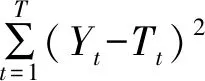
λ为平滑参数，是对趋势性部分Tt波动的惩罚因子(λ为正值)，不同的λ值决定了不同的周期方式和平滑度。对于参数λ的取值，就年度数据而言，λ=100(Backus and Kehoe，1992)；就季度数据而言，λ=1 600(Hodrick and Prescott，1980,1997)；就月度数据而言，λ=14 400，这也是Eviews软件的默认值。

2 结果与分析

2.1 调查样本

研究表明，2010年4月至2017年5月期间，新疆枣果的价格经历了较大幅度的波动，平均价格为67.26元/kg；其标准差为35.02，偏度系数为0.543，数据呈右偏分布，峰度系数为-0.979，数据分布较为分散。

从价格变动情况分析，与上月同期相比，其中46个月的价格出现下跌，所占比例达到55.42%，下跌幅度最高达到42.31%，2011年12月到2012年1月，价格从130元/kg跌至75元/kg；而价格上涨的月份不足一半，上涨幅度最高达到48.15%，2015年10月至2015年11月，价格从27元/kg增长到40元/kg。新疆枣果的市场价格不太稳定，波动幅度较大，2010年4月至2017年5月间，价格平均月度增长率为-1.06%，呈现整体下降趋势。表1

表1 2010年4月至2017年5月新疆枣价
Table 1 Prices of Xinjiang Jujubes in 2010.4-2017.5 (Yuan / kg)

日期Date价格Price日期Date价格Price日期Date价格Price日期Date价格Price日期Date价格Price2010.41202011.11262013.4622014.1502016.4232010.51182011.111252013.5602014.11522016.5252010.61162011.121302013.6602014.12542016.6222010.71172012.1752013.7622015.1522016.7212010.81152012.2802013.8582015.2482016.8282010.91252012.3722013.9542015.3442016.9382010.11282012.4672013.1682015.4432016.1352010.111362012.5702013.11652015.5402016.11282010.121202012.6652013.12662015.6382016.12302011.11152012.7642014.1722015.7402017.1262011.21162012.8672014.2702015.8352017.2172011.31132012.9672014.3602015.9292017.3262011.41122012.1722014.4542015.1272017.4232011.51162012.11732014.5482015.11402017.5162011.61122012.12852014.6402015.12292011.71262013.1722014.7422016.1312011.81282013.2682014.8412016.2262011.91232013.3682014.9482016.324

数据来源：中国枣网http://www.cnzao.com/

Data Sources: CNZao http://www.cnzao.com/

数据来源：中国枣网

Data Sources: CNZao http://www.cnzao.com/

图1 2010年4月至2017年5月新疆枣价月增长率
Fig.1 Monthly Growth Rate of Xinjiang Jujube in 2010.4-2017.5

2.2 季节调整法下的价格特征

2.2.1 价格整体波动

研究表明，剔除消费价格指数(CPI)变动的影响后，2012年前，新疆枣价处于高位波动，价格基本保持在105～125元/kg，平均价格为115.41元/kg，标准差为6.35，价格波动幅度不大，平均月度增幅为0.46%，；2012年后，新疆枣价呈现波动下行趋势，在2012年期间，价格最大跌幅达到42.53%；价格变动存在一定的周期性特征，年度价格数据均呈现由高到低再变高的规律。时间序列波动的幅度没有呈现出随时间推移而逐渐增大或减少的趋势，研究选取加法模型分析价格波动特征。图2

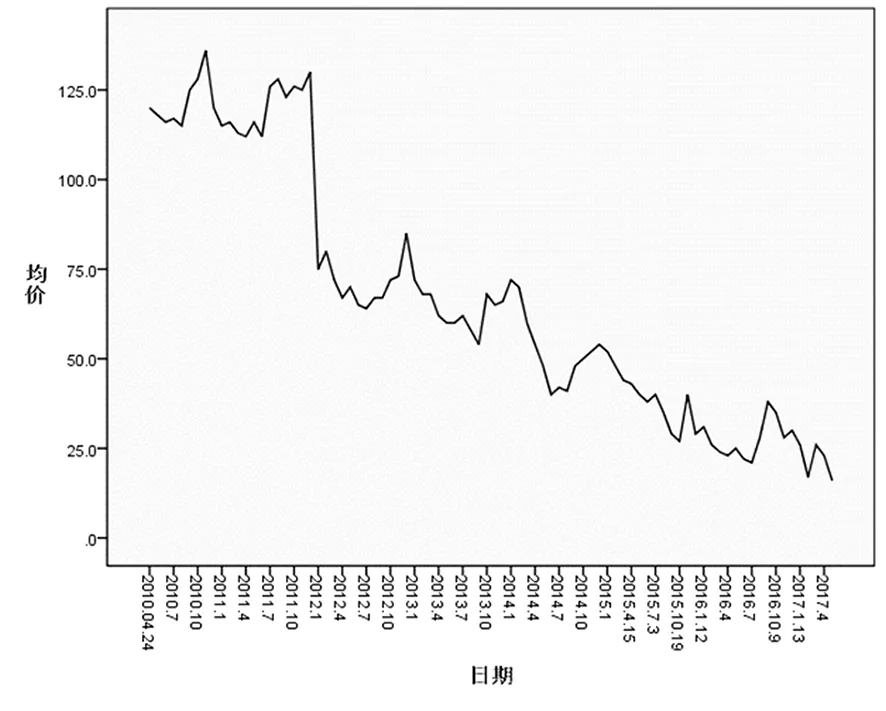
图2 新疆枣价波动的时间序列
Fig.2 Time Series of Zodiac Fluctuations in Xinjiang

2.2.2 价格的季节性波动特征

研究表明，新疆枣价季节周期性因素值在-7至10波动，每年的11月和12月的价格会达到季节性波动的最高点，4月、5月和6月会达到季节性波动的最低点，价格的季节性波动特征呈现出明显的V字型。通常，价格与枣果的上市时间密切相关。每年收购期开始后，市面上枣果平均品质较高，高品质枣果在周年供应期中所占比例达到最高，市场需求旺盛、需求量猛增，价格呈现上涨趋势；随着市场需求逐渐饱和、优质枣果逐渐减少，收购中后期的价格开始回落，至次年新枣上市前，价格降至最低。2010年至2017年期间，新疆枣价的季节性波动特征明显且基本保持稳定。图3

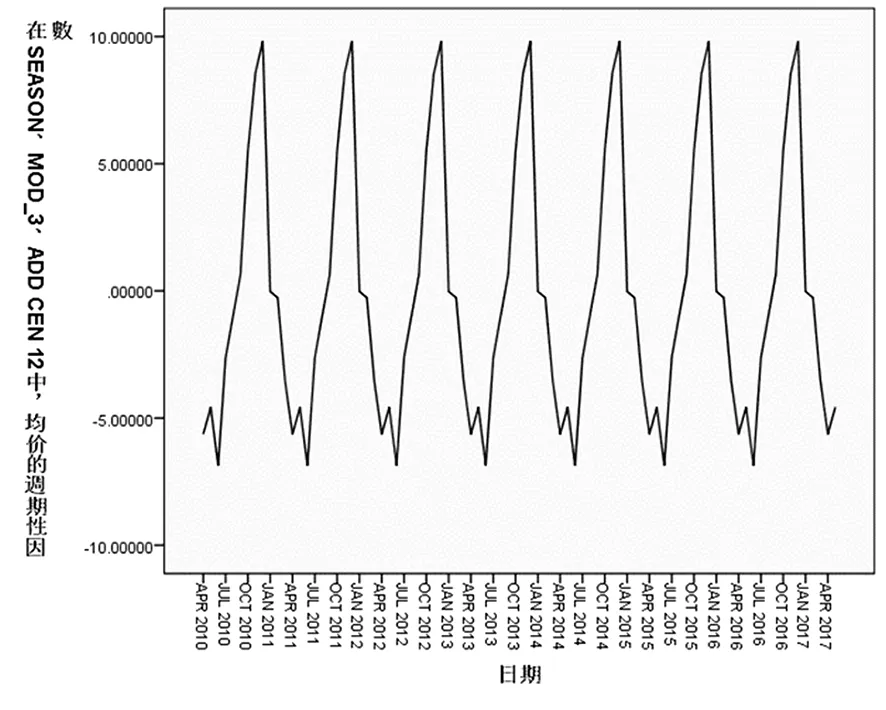
图3 新疆枣价的季节波动特征
Fig.3 Seasonal Fluctuations of Prices of Jujubes in Xinjiang

2.2.3 剔除季节因素后的价格波动和趋势变动

研究表明，剔除季节因素后，新疆枣价最高值为125.36元/kg，最低值为22.03元/kg，平均价格为66.36元/kg；其标准差为34.63，偏度系数为0.525，峰度系数为-1.051。调整后，具有趋势周期特征的新疆枣价仍呈现明显下降趋势，但是变化更加平缓；枣价在2012年期间经历了断崖式下跌后，继续呈现阶梯状缓慢下降趋势。表2，图4，图5

表2 2010年4月至2017年5月季节调整后的价格
Table 2 Prices of Xinjiang Jujubes in 2010.4-2017.5 after Seasonal Factors Analysis (Yuan / kg)

日期Date价格Price日期Date价格Price日期Date价格Price日期Date价格Price日期Date价格Price2010.4124.72 2011.1120.92 2013.467.81 2014.144.58 2016.428.36 2010.5123.69 2011.11114.23 2013.566.54 2014.1145.23 2016.528.32 2010.6121.62 2011.12104.92 2013.665.07 2014.1246.25 2016.627.84 2010.7120.39 2012.190.89 2013.762.61 2015.148.00 2016.728.16 2010.8120.14 2012.281.64 2013.860.25 2015.248.53 2016.829.70 2010.9121.90 2012.375.78 2013.958.23 2015.348.12 2016.930.23 2010.1121.92 2012.474.48 2013.158.03 2015.447.03 2016.127.92 2010.11120.79 2012.572.77 2013.1159.12 2015.545.65 2016.1124.57 2010.12117.14 2012.670.95 2013.1262.03 2015.643.73 2016.1222.03 2011.1115.78 2012.768.94 2014.165.44 2015.740.28 2017.122.44 2011.2115.53 2012.867.58 2014.266.42 2015.835.14 2017.223.53 2011.3117.01 2012.966.57 2014.363.89 2015.930.45 2017.325.23 2011.4118.03 2012.167.14 2014.458.70 2015.126.58 2017.426.25 2011.5119.99 2012.1168.34 2014.553.21 2015.1126.12 2017.526.77 2011.6122.40 2012.1270.36 2014.648.51 2015.1225.59 2011.7124.94 2013.171.00 2014.745.72 2016.127.00 2011.8125.36 2013.270.53 2014.844.58 2016.227.08 2011.9123.45 2013.369.23 2014.944.79 2016.328.12

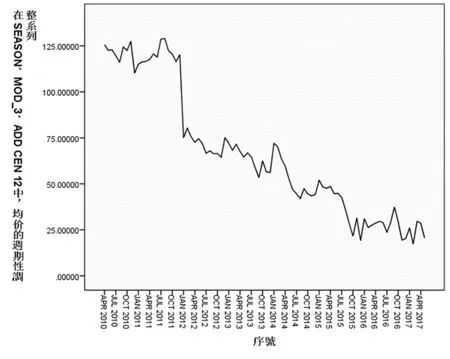
图4 新疆枣价剔除季节因素后的价格波动
Fig.4 Price Fluctuation of Jujubes in Xinjiang after Seasonal Factors Analysis

图5 新疆枣价的趋势循环序列
Fig.5 Price Trend Curve of Xinjiang Dates

2.3 基于HP滤波法的长期趋势和周期性

2.3.1 新疆枣价格的长期趋势

研究表明，HP滤波法的分解效果较好，长期趋势值和Census X-12季节调整法下的数值之间的拟合优度较高，达到了94.8%并且在1%的水平上显著，说明长期趋势曲线能够较好反映新疆枣价的变动。图6

图6 2010.4～2017.5新疆枣价的长期趋势
Fig.6 Decomposition of Long-term Trend for the Prices of Xinjiang Dates during 2010.4-2017.5

从长期趋势值看(HP滤波值)，从2010年4月至2017年5月新疆枣价呈现持续下跌趋势且下降幅度逐渐增加。枣价下跌过程大致可分为三个阶段：第一阶段，2010年4月至2011年12月，枣价下跌幅度在1%～2%；2012年1月至2016年12月，枣价下跌幅度在2%～3%，其中，2013年1～11月间，枣价下跌速度有所放缓，下跌幅度基本保持在约2%的水平；2017年1～5月间，枣价下跌幅度3%以上。表3

表3 2010.4至2017.5新疆枣价HP滤波长期趋势值
Table 3 HP Long-term Trend for the Unit Price of Xinjiang Dates during 2010.4-2017.5 (Yuan/kg)

日期Date价格Price日期Date价格Price日期Date价格Price日期Date价格Price2010.4131.68 2012.488.38 2014.453.39 2016.429.97 2010.5130.00 2012.586.51 2014.552.26 2016.529.19 2010.6128.32 2012.684.67 2014.651.14 2016.628.41 2010.7126.64 2012.782.87 2014.750.04 2016.727.65 2010.8124.95 2012.881.10 2014.848.95 2016.826.90 2010.9123.27 2012.979.38 2014.947.88 2016.926.16 2010.10121.57 2012.1077.70 2014.1046.82 2016.1025.42 2010.11119.87 2012.1176.06 2014.1145.78 2016.1124.69 2010.12118.15 2012.1274.46 2014.1244.74 2016.1223.97 2011.1116.42 2013.172.91 2015.143.72 2017.123.25 2011.2114.68 2013.271.39 2015.242.71 2017.222.54 2011.3112.91 2013.369.91 2015.341.71 2017.321.82 2011.4111.13 2013.468.47 2015.440.73 2017.421.11 2011.5109.33 2013.567.07 2015.539.75 2017.520.40 2011.6107.50 2013.665.69 2015.638.78 2011.7105.65 2013.764.35 2015.737.82 2011.8103.77 2013.863.04 2015.836.88 2011.9101.87 2013.961.76 2015.935.95 2011.1099.95 2013.1060.50 2015.1035.04 2011.1198.02 2013.1159.27 2015.1134.15 2011.1296.08 2013.1258.06 2015.1233.28 2012.194.14 2014.156.87 2016.132.43 2012.292.20 2014.255.69 2016.231.59 2012.390.28 2014.354.53 2016.330.77

2.3.2 新疆枣价格的周期性成分

周期性成分是剔除长期趋势后的波动值，周期性成分分析表明新疆枣价的变化呈现出显著的周期性波动特征。研究按照“波谷-波峰-波谷”的周期性趋势变化特征，将新疆枣价的变动划分为不同的波动周期。从2010年4月至2017年5月，新疆枣价经历了4个完整的波动周期。新疆枣价的波动规律和特征，第一周期从2010年4月至2012年3月，第二周期从2012年4月到2014年8月，第三周期从2014年9月至2015年10月，第四周期从2015年11月到2016年12月。图7，表4

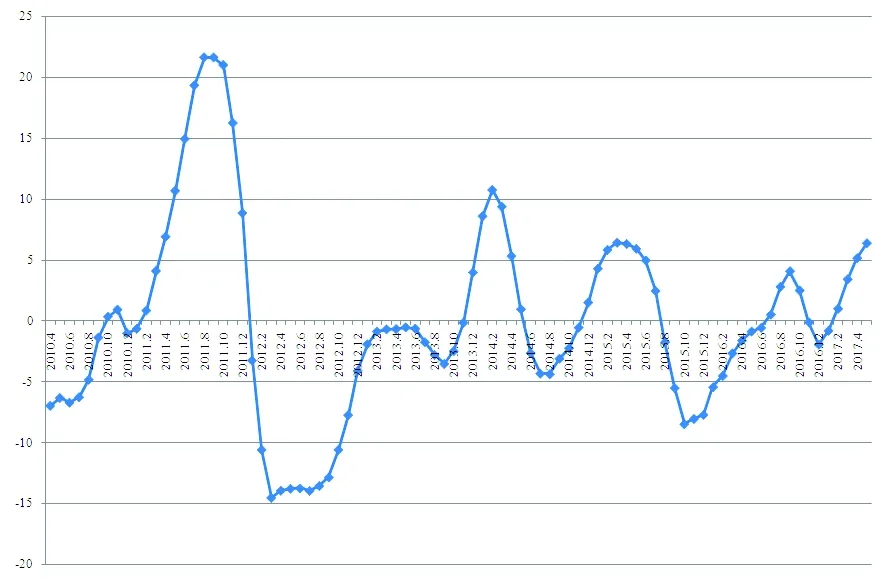
图7 2010.4～2017.5新疆枣价变异率波动
Fig.7 The Mutation Rate of the Prices of Xinjiang Dates during 2010.4-2017.5表4 HP滤波法下的价格波动周期特征Table 4 The Characteristics of Price Fluctuation Cycle under Hodrick-Prescott Filter

类别第一周期第二周期第三周期第四周期第五周期(不完整)起止时间2010.4～2012.32012.4～2014.82014.9～2015.102015.11～2016.122017.1～波长(月)24291414波动指数(%)波峰21.6910.666.444.07波谷-14.47-4.38-8.27-1.94波幅36.1615.0414.716.01周期类型缓升陡降型缓升陡降型陡升陡降型缓升陡降型

从波动周期的波长情况看，价格波动时间跨度逐渐缩短。第一周期为24个月，第二周期为29个月，第三周期和第四周期分别为14个月。整体来看，波动周期相对较短，基本保持在1～2年，略微呈现出波动周期缩短的趋势。价格波动周期由长变短的变化，新疆枣果的价格起伏波动正变得更加频繁。

从波动幅度看，第一周期波幅为36.16%，波动幅度最大，第二周期波幅大幅下降到15.04%，第三周期的波幅与前一周期相比变动不大，为14.71%，第四周期的波幅又明显下降，仅为6.01%。新疆枣价的波动幅度较大，价格变化剧烈。特别是第一周期的波动幅度远超后三个周期，新疆枣价在第一周期出现了超常规的大幅上升后迅速下跌，仅用7个月的时间价格就跌到波谷。第二周期和第三周期虽然价格也有较为剧烈的起伏，但是波动幅度保持在15%左右；第四周期价格波动相对较为缓和。新疆枣价在4个完整波动周期中波幅逐渐减小。

从波动指数来看，第一、二、四周期的价格涨幅高于跌幅，而第三周期的价格跌幅高于涨幅；比较各个周期的波峰值，波峰值呈现下滑趋势，从第一周期的21.69%下跌至第四周期的4.07%，下滑速度从50.85%逐渐降至36.80%，下滑速度逐渐趋缓。在周期性振荡中，新疆枣果的价格虽然整体下滑但是日趋稳定。表5

从波动周期类型看，第一、二、四周期为缓升陡降型，价格上涨持续时间长，价格下跌持续时间短，第一、二、四周期的价格上涨持续时间分别是16个月、23个月和11个月，而价格下跌持续时间分别是7个月、6个月和3个月；第三周期为陡升陡降型，价格上涨持续时间和价格下跌持续时间均较短，价格从波谷涨至波峰、从波峰再次跌至波谷只经历了7个月时间。在四个波动周期中，价格持续上涨时间变动较大，整体呈现逐渐缩短的趋势；前三个波动周期中，持续下跌时间变化差异不明显，第四周期的持续下跌时间明显缩短。HP滤波法下新疆枣价波动周期类型的变化表明，2010年前后新疆枣价飞速增长2012年结束，此后价格增长步幅逐渐放缓，价格很难继续在长时间内保持高位运行；价格在达到波动周期最高值后，会快速出现回落，持续保持低位运行的时间也逐渐缩短。表4，表5

表5 HP滤波法下的价格波动周期
Table 5 Price Fluctuation Cycle under Hodrick-Prescott Filter

特征第一周期(2010.4～2012.3)第二周期(2012.4～2014.8)第三周期(2014.9～2015.10)第四周期(2015.11～2016.12)波峰时间2011.82014.22015.32016.9波谷时间2010.42012.32014.82015.102016.12上涨持续时间(月)1623711下跌持续时间(月)7673

3 讨 论

3.1 生产规模扩大

纵观全国枣产量的变化情况，1973年至1990年期间经历过高至20%以上的增长和低至10%以上的下跌，涨跌幅度较大但是总产量并未出现明显上涨，平均产量仅为411 878 t。1990年后枣产量呈现增长趋势，除1996年、1999年和2007年出现不足1%的跌幅外，其余年份均呈大幅增长态势，1991年至2016年间的平均涨幅约为12.40%。2000年后，随着新疆枣产区的种植面积扩张，全国枣产量呈现高速增长趋势，2000年至2016年期间的平均增长速度达到12.83%；新疆枣产量的平均增长速度高达48.31%，其中，2009年的增长率达到历史最高值119.95%。由于新疆枣产业生产规模的扩大、产量急剧增长，2012年，枣果的市场供求状况开始发生巨大变化，市场从供不应求、价格虚高，转变为供过于求。目前枣果市场仍然处于供过于求的状况，然而当前的“供过于求”实则为“供求结构性不平衡”，中低端产品供过于求、高端产品供不应求，造成了市场价格的持续下跌。

3.2 集中上市、集中囤购

枣果价格的季节性波动特点，与枣果过于集中上市，以及消费者集中囤购枣果并“周年消费”的模式紧密相关。枣果集中上市与其生长规律、生产技术直接相关，枣果尚未实现周年供应，在每年10月枣果大批成熟之际，市场上高品质枣果充裕，消费者和加工企业竞相大量采购新上市枣果。在此期间，受新枣上市、平均品质较高、需求旺盛等原因的综合影响，市场价格较高。每年过年后，随着当年市场需求逐渐得到满足，市场上枣果的品质整体下滑，价格也出现明显回落，价格下降趋势持续至新枣上市，由此产生了价格季节性波动的特征。

3.3 市场日趋成熟稳定

新疆枣果市场价格呈周期性变化的特点符合经济周期规律，枣果价格波动频率加快、波动幅度减小、峰值降低的周期性波动规律表明新疆枣果市场日趋成熟，市场价格逐渐趋于稳定，难以长时间维持在较高水平。当新疆枣果市场规模不断扩大，投资、消费均逐渐回归理性，枣果价格逐渐趋向市场均衡价格。

3.4 优化供给结构

品种升级，解决新疆枣果以灰枣和骏枣为主的单一品种结构问题；结构升级，减少需求过剩的中低端枣产品的供给，增加高端枣产品的供给，满足有效需求，提升整体价格水平，解决结构性供需失衡的问题；加工升级，能够有效调节供应量和供应时间，缓解价格的剧烈波动的问题。当前市场上制干枣所占比例高达70%以上，消费者对于精深加工枣产品的需求尚未被满足，加工升级能够在供给总量较为充足的前提下，消化大量枣果，缓解由于供给总量过多造成的价格下行压力；枣类加工品实现周年供应，有效避免上市时间过于集中对市场价格造成的扰动。

3.5 调整供应周期

调整枣果上市时间和上市周期是稳定市场价格的有效措施。为了解决集中上市造成的价格季节性波动幅度较大的问题，可通过提高仓储技术、降低仓储成本，逐步实现枣果上市时间周年化，以稳定释放供给、稳定市场价格；加快建立并完善枣果期货市场和保险市场，利用金融市场规避现货市场价格波动。

4 结 论

4.1 新疆枣果的市场价格呈现明显下降趋势且下降幅度逐渐加大。在2012年前，市场价格基本保持较高水平，2012年价格下跌，下跌幅度超过10%，价格继续呈现下降趋势，当价格逐渐逼近生产成本时，价格下跌速度开始有所减缓。新疆枣产业生产规模的扩大、产量急剧增长，造成市场结构性供过于求，是价格下降的原因。

4.2 新疆枣果价格的季节性变化特征明显。价格季节性变动呈现明显的V字型特征，季节成分波动的波峰出现在每年11～12月，波谷出现在次年4～6月，这与枣果上市时间、供应特点和消费特点有直接关系，季节成分对价格的影响程度较大，解决集中上市问题能够缓解价格的季节性大幅波动。

4.3 新疆枣果价格呈现周期性波动规律。自2010年3月以来，新疆枣果的市场价格波动已经经历了四个完整波动周期，第五个周期正处于上涨阶段。纵观以往价格波动周期，价格波动幅度逐渐减小，从36.16%下降至6.01%；但是，价格波动更加频繁，波动周期从24个月已经大幅降至14个月；波峰值也在不断下降。