高等数学理论在高中数学教学中的渗透

唐 剑，王振新，李 群，孙娓娓

(1.阜阳师范学院 数学与统计学院，安徽 阜阳 236037；2.太和中学，安徽 阜阳 236600)

高等数学课程不但与其它学科联系密切，而且亦是理科、工科及经管等专业学习的基础，是整个大学课程学习的开端。清晰的内容结构和作为数学应用的基础是高等数学课程的特点，使其成为大学数学的基础课程之一[1]。高等数学课程是我们建立知识体系的主要奠基学科，也是高中数学的发展和延伸。高等数学课程作为学习后继专业课程的基础，其教学目的主要是为了让学生了解基本的知识和方法，培养其数学思维方式。

高等数学课程包含了许多分支学科，我们在学习中可以发现，高等数学所研究的对象较高中数学来说有了更深层次的追求，涉及了很多新的概念，同时也强调了许多不同的量。我们不难发现，高等数学和高中数学的研究内容及特点有很多相似之处，但是其研究和运算方法却更加繁杂。正因如此，高等数学课程在知识内容上是高中数学的继续与拓展，在观念上是高中数学的深化与发展，在思想方法上是高中数学的沿袭与扩张[2]。本文将从知识方面、思想方面、学科自身性质方面及观念方面探讨高等数学课程与高中数学的联系，同时分析并归纳高等数学理论在高中数学解题中的若干应用，探索高等数学理论在高中数学教学中的渗透作用。

1 高等数学课程与高中数学的联系

非数学专业的学生在进入大学校门后最先接触的数学基础课程就是高等数学，该课程为非数学专业的三大数学类公共基础课程之一，这表明了它在数学基础课程中的重要地位。在接触高等数学课程后，我们不难发现它和高中数学联系十分密切，该课程是联系初等数学、大学数学的枢纽。有些知识由于局限性使得在高中数学中我们无法深入了解，但是到了高等数学课程中就很容易得到解决。下面我们主要探讨高等数学课程与高中数学在知识方面、思想方面、学科自身性质方面及观念方面的联系。

1.1 知识方面的联系

高中数学课程中我们掌握了函数的概念、性质以及相关运算法则。学习了高等数学课程之后，拓宽了我们对函数更多的认识，深入学习了函数的性质，如函数的单调性、有界性、连续性、凹凸性及函数的极值等性质，相关的运算法则也有了较为严格的定义。同时，在高等数学课程中不仅对高中数学中所学习的函数导数给出了精确的定义，而且也拓宽了函数导数的性质及相关应用，尤其对函数导数的几何意义做了深入剖析。另外，高中数学课程中所学习的各种初等函数、向量、参数方程、坐标系等知识为进一步学习高等数学课程奠定了理论基础。

综合以上，不难看出高等数学课程和高中数学课程有很多联系。它不但让我们了解了许多高中数学中未能理解清楚的问题，而且以各个知识点作为实例，由浅入深，为高等数学的学习打下了坚实的基础。

1.2 思想方面的联系

1.2.1 抽象化思想

小学数学通过数具体物体的数量来学习数字，把我们引入了算术运算时期。中学数学通过未知数x，带领我们走进研究简单函数与方程的时期。高等数学课程开始研究抽象的函数问题，引入我们现在所常见的导数、积分、微分方程及多元函数等，使得数学的研究对象发生了巨大变化，这也是高等数学课程抽象化的原因。

1.2.2 类比推理思想

类比推理是数学教学中的一种常用思维方法。在数学学习及教学中，合理使用类比推理方法可以使抽象的数学知识变得具体而生动[3]。例如，在高中数学中，我们要得出两平面的位置关系是通过两直线的位置关系得到的。在高等数学课程中，由高中数学中直线、椭圆、双曲线和抛物线的有关知识可类比推理出一些空间曲线及空间曲面的方程及其相关性质；由高中数学中的平面上点到直线的距离公式可类比推出空间中点到平面的距离公式。

1.2.3 严格的逻辑推理方法

由于理解能力有限，高中数学中很少遇到严格的定义，一些推理过程也很简单易懂，即使像几何问题，由于图形较单一，通常可以用直观图形来展示。从记忆中搜索高中时接触到的证明方法，大概也只有反证法和数学归纳法，像这样的也并不是详细了解，当初学习时只学到了部分皮毛，或者说只是照搬硬套老师教的，并不是自己真正理解了其中的含义。学习了高等数学课程之后会有明显的感觉，它与高中数学的理论思想完全不同，与之相比较更加严谨，逻辑推理更加清晰，各个问题都有严格的定义，刚开始理解起来或许比较困难，但是时间久了，自然会发现其中的奥妙所在。

1.2.4 构造性方法

构造性方法对于我们来说最典型的是高中数学学习的二元一次方程组的求解方法。高等代数课程用到构造性方法就更广泛了，可以利用它来解题，也可以用来证明定理。例如，在高等代数课程中证明一个命题，我们可以通过构造反例来解决，选择特殊情形和极端情形作为反例，进而揭示判断的虚假性；在证明某些不等式或方程有根的问题时，我们可通过构造辅助函数的方法，并利用函数的单调性、奇偶性、凹凸性、微分中值定理、积分中值定理等知识来证明相关问题。另外，构造法在数列极限、函数的三角级数展开式及相关几何问题中也有着极其广泛地应用。构造法不仅方便解决问题，也使得我们对概念理解得更加透彻。

1.2.5 分类思想

数学分类思想是依据数学研究对象本质属性的差异性，将其分为不同类别的一种数学思想。它不仅是一种重要的数学思想，更是一种重要的数学研究方法[4]。分类思想，贯穿于整个高中数学的全部内容中。高中数学中涉及的数学概念一般是对研究的对象进行分类来定义的，如对数集的分类，对三角形的分类及对方程的分类等。然而，分类思想在高等代数课程中也是屡见不鲜的。例如，将函数分为连续函数与不连续函数两类，将微分方程分为齐次的与非齐次的两类，将级数分为收敛的与发散的两类等。另外，在高等数学的解题过程中，分类讨论的方法也是经常用到。

实践表明，对于具有一定综合性和逻辑性的数学问题，一般都可采用分类思想加以讨论。数学分类思想对于培养学生全面分析问题和解决问题的能力起到了较为重要的作用。因此，在高中数学及高等数学教学中我们要向学生不断地渗透分类思想，时刻引导他们采用分类讨论方法解决实际问题。

1.3 学科自身性质方面的联系

由于初等数学到高等数学在研究问题和处理方法上有着很大的区别，人们通常认为大学数学中所学的专业知识在高中数学中几乎无用。其实这是一种错误的理解，正是因为有了这样的区别，我们才能从高中数学的解题思维定式中走出来，通过一种更深远的眼光，站在一个更高的角度来看待高中数学问题。

高等数学课程是高中数学的延伸和提高，只有对其基础知识充分掌握，才能适应数学的发展和教材的改革[5]。高等数学知识不仅可以提高学生的学习兴趣，还可以拓宽视野，同时也能应用到中学数学题的解法中去，使复杂问题趋于简便化。

1.4 观念方面的联系

我们起初在高中数学中所产生的对于相关概念的理解，通过高等数学的学习都将对我们之前所学习的知识形成系统的概括，使我们认识地更加深入和透彻。我们通过对比二者之间的区别与联系，不难看出我们所要研究的对象一是数量之间的关系，另一个则是空间的形式。

2 课程内容在高中数学解题中的应用

众所周知，高等数学课程是理学、工学、经济学、金融学、计算机科学、管理学、教育学、心理学等学科专业课程教育的开始，是高等学校理、工、经、管等专业的入门数学公共课程之一，也是从高中数学到大学数学过渡的桥梁[6]。因此，高等数学研究的内容与高中数学内容有着紧密的联系。例如，一些在高中数学教学与学习中因为受到所学知识的局限而没办法深入讨论的问题在高等数学课程中得到了圆满的解决；一些在高中数学中无法深入讲解的基本概念、方法，在学习了高等数学这门课程以后，居高临下，使人心中豁然开朗，进而拓宽了高中数学教师的视野，为他们选择适当的教学方法指明了方向。下面我们将根据高等数学课程内容的特点，主要分析、归纳该课程中导数理论、极限理论、向量理论及积分理论在高中数学解题中的应用。

2.1 导数理论在高中数学解题中的应用

导数理论是高中数学的重要内容，但在高中数学中主要侧重于学习导数的基本运算，对导数的严格定义、理论证明和重要应用没有深入讲解。另一方面，导数理论也是高等数学课程研究的主要内容之一，它使各个章节的内容联系得更加紧密，为高等数学的基本内容提供了理论基础。导数理论与高中数学有着密切的联系，该理论在初等数学中有着非常重要的应用，对高中数学解题起到了“居高临下”的作用。相比高中数学内容，高等数学的导数理论无论是深度、广度还是规范化程度都明显增强了。在目前的高中数学教材中，导数理论处于一种特殊的地位。为使学生能够更好地理解函数的性态以及掌握函数思想在数学上的应用,对于一些不能采用或者难以采用初等数学方法解决的问题，一般可通过建立函数关系式，运用函数思想，并借助于导数这个有力工具来研究其性质，轻松简捷地获得问题的解决，这充分体现了导数工具性和应用性的重要作用。在高中数学课程改革背景下,导数知识已经作为高中数学的重要模块之一，这为高等数学课程教学奠定了坚实的基础。反过来，高等数学课程中的导数理论是高中数学中相关内容的发展与深化，其应用非常广泛，几乎涉及到高中数学内容的各个方面，对高中数学的教学与竞赛具有理论指导意义。

例 1 设函数f(x)=axn(1-x)+b(x＞0)，其中n为正整数，a,b为常数。又曲线y=f(x)在(1,f(1))处的切线方程为x+y=1。

（1）求a,b的值；

（2）求函数f(x)的最大值。

解 （1）由于f(1)=b,从而由点(1,b)再直线x+y=1上 可 得 ：1+b=1,即b=0。因 为f′(x)=anxn-1-a(n+1)xn,所以f′(1)=-a。又因为切线x+y=1的斜率为-1，所以-a=-1,即a=1。故a=1,b=0。

（2）由（1）知，f(x)=xn(1-x)=xn-xn+1。于是，有

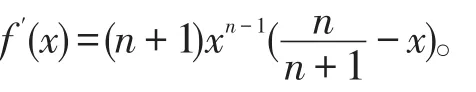
令f′(x)=0，解得即f′(x)在 (0,+∞)上有唯一零点又在上，f′(x)＞0，故f(x)单调递增；而在上，，故f(x)单调递减。因此，f(x)在(0,+∞)上存在最大值，且最大值为

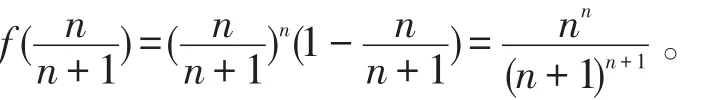
一直以来，函数值域的求解问题是高中数学中的重点与难点，其求解方法因题而异，难以掌握。有的题目用常规方法很难求解，但若采用导数来求解，则较为方便。下面举例说明之。

解 显然，函数f(x)的定义域为，由于

又由于

注1 对于有些函数值域的求解问题，可首先求出函数的定义域，然后再根据定义域判断该函数的导函数的正负，进而求出函数的值域。此方法具有一定普遍性和推广价值。

2.2 极限理论在高中数学解题中的应用

极限是高等数学课程内容中的基本概念，是研究微积分学的重要工具。极限理论在高中数学与高等数学中起着承上启下的作用，下面通过举例阐述极限思想在高中数学里的体现。通过这些例题学习与分析来提高对极限思想方法的理解力，进一步揭示用极限思想方法解决问题的简捷性和优越性。

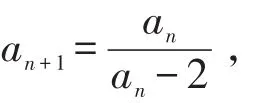
问是否存在实数a,b使得对于任意正整数n恒成立？若存在，给出证明；若不存在，说明理由。

证明 假设存在实数a,b使得

对于任意正整数n恒成立，则

若a=0，则将a1=1代入，可得，此时，则数列{an}是以1为首项，为公比的等比数列，显然，，不符合题意，故舍去。

若a=3，则将a1=1代入，可得b=-3，此时同样通过验证a1,a2也可得出矛盾。

综上可知，满足题意的a,b不存在。

例4 证明：所有双曲线与它们的渐近线只能无限靠近，但绝不会相交。

图1 例4的示意图

因此，当点M远离原点时，该点到渐近线的距离也趋近于0，但无论x有多大，这个距离都不可能为0。

2.3 向量理论在高中数学解题中的应用

向量不仅是高等数学中最重要、最基本的概念之一，也是研究高中数学的重要工具和手段。在高等数学课程中，引入了空间向量的长度、数量积、距离等概念，并给出了向量夹角的坐标计算公式,这些正是中学数学中平面向量的直接推广。而且高等数学课程中的向量理论，有助于我们对高中数学几何空间中向量长度、距离、夹角等度量概念的更深刻理解。例如，利用数量积的相关性质，我们可得出著名的余弦定理、勾股定理、柯西不等式等重要结论。因此，高等数学课程中的向量理论为高中数学的一些基本内容提供了理论依据。在普通高中数学新课改中“,向量”是必修模块之一[7],是高中数学教学内容中非常重要的组成部分，相对于课本中的其它知识，向量比较抽象难懂，再加上很多学生对向量在具体解题过程中的应用了解甚少，使得向量理论在高中数学整体的解题方式上显得比较少而且较难。但是，在真正掌握了向量的解题规律之后，我们能够发现运用向量进行解题，一般步骤较少，只要找出诀窍就可以在短时间内完成解题。因此，掌握向量在高中数学解题中的应用备受重视。由于向量是沟通代数、几何及三角函数等内容的桥梁，因此，向量在高中数学解题中具有较为广泛的应用。下面举例加以说明。

例5 已知定点F(1,0)，动点P在y轴上运动，过点P作PM交x轴于点M，并延长MP到点N，且。

（1）求点N的轨迹；

（2）直线l与N的轨迹交于A、B两点，若，且，求直线l的斜率k的取值范围。

解 （1）设P(0,b),M(a,0)，则kPF=-b,。由于，从而k·k=-1,即PFPMa=-b2，故M(-b2,0)。又，即P为MN的中点，从而N(b2,2b)。因此，N的轨迹方程为：y2=4x，其轨迹为以F(1,0)为焦点的抛物线。

（2）设l:y=kx+b，与y2=4x联立，得

设A(x1,y1),B(x2,y2)，则y1,y2是（*）式的两根，且。由，得：xx+yy=-4，1212即从而

故b=-2k。因此，直线方程为

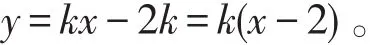
综上可见，向量是一种常用的解题工具，其在高中数学问题中应用广泛。因此，我们应该有意识地将已知问题转化为向量问题，进而借助于向量的知识加以解决。这就要求高中数学课堂教学中不仅要求学生掌握向量的相关知识，还要灵活应用，强化学生对向量的运用能力，提高学生的解题效率，进而帮助学生减轻解题的负担。

2.4 积分理论在高中数学解题中的应用

定积分与重积分是高等数学课程中的重要内容，其概念的引入主要是借助于极限这一工具。高等数学中的积分理论把高中数学中处理“不变”问题的方法应用于处理“变”的问题；把高中数学中处理“直”的问题的方法应用于处理“曲”的问题；把高中数学中处理“有限”问题的方法应用于处理“无限”的问题。鉴于此,对于高中数学中无法解决的很多问题,如任意曲线所围成的面积、变力沿曲线所作的功等,积分思想给出了对高中数学的一些指导,从而使得相关问题较容易地获得解决。另外，积分理论也是高中数学中一些熟知结果的证明依据，例如球的体积为，圆的面积为πR2，椭圆的面积为πab等,这些结果在高中数学教材中基本上没有给出严格证明,即使给出了证明,其方法也很复杂，难以理解。实际上，以上结果运用高等数学中的定积分和重积分的知识是很容易求得的，这里不再详述，读者可参见文[8]。

从以上分析,足以看出高等数学课程内容在高中数学中具有广泛的应用。作为高师院校的数学教师，我们不但要清醒地认识到，更重要的是我们应该在日常教学中不断地向学生讲述“这些应用”，灌输这种思想，使他们能够深刻地领会这些思想，进一步开拓他们的视野，使他们更好地掌握用高等数学解决初等数学的方法，为高等数学教学建立起形象的数学模型[3]，从而为学生们在将来的教学实践中充分发挥这种“居高临下”的作用提供了理论基础。

3 小结

高等数学课程与高中数学课程在思想方法方面的联系非常紧密，其主要体现在抽象化思想、分类思想、类比推理思想、构造化思想与方法等方面。因此，充分意识到高等数学课程与高中数学的联系对比，不仅可以增强高等数学课程对培养高中数学教师的指导作用，同时也可以降低该门

课程的学习难度。学生通过对高等数学这门课程的学习，不仅加深了他们对高中数学内容的理解，同时还拓宽了他们的知识视野，进一步培养了学生发现问题、分析问题和解决问题的能力。因此，对于师范类专业的学生而言，在他们毕业之后的教学工作中，不能仅仅将视野局限于高中数学，应有效利用高等数学的思想、观点和方法，从更深层次、多角度、全方位地掌握高中数学的教学体系，深刻地领会高中数学课程的教学内容，深刻理解高中数学问题的实质与背景，全面掌握利用高等数学的知识、思想和方法来分析、处理和解决高中数学问题的能力,揭示高中数学的解题方法。只有这样，才能更有利于提高学生的数学思维能力，拓宽解题思路，加强学生对数学问题的解题技巧。

参考文献：

[1]孙娓娓，唐 剑，王志刚，等．关于高师院校高等数学教学改革探讨[J].阴山学刊（自然科学版），2015,29(4):89-91．

[2]李 岚.高等数学教学改革研究进展[J].大学数学，2007,23(4):20-26．

[3]牛海军.初等数学与高等数学教学衔接问题的研究[D].大连：辽宁师范大学，2008．

[4]张奠宇.数学教育研究导引[M].南京：江苏教育出版社，1998．

[5]陈利娅，赖 霞.高等数学教学存在的问题及改进措施[J]．高等教育研究，2013,30(4):32-34．

[6]薛欢庆，方 正.浅谈高等数学在中学数学解题中的作用[J].牡丹江师范学院学报（自然科学版），2010(3):73-74．

[7]中华人民共和国教育部.普通高中数学课程标准:实验[M].北京：人民教育出版社，2003：24-26．

[8]同济大学数学系.高等数学[M].第7版.北京：高等教育出版社，2014：276-284.