吊杆损伤对外倾单肋式曲线钢拱桥自振特性的影响

金其莉，陈建兵，尉洪利 ，汪一意

(1.苏州科技大学土木工程学院，江苏 苏州 215011；2.中交一公局第二工程有限公司，江苏 苏州 215011)

0 引言

外倾单肋式拱桥是指拱肋向外倾斜，通过拱肋外倾来平衡桥面部分荷载的异形拱桥[1]，其外形美观新颖,能够给人带来一种奇特的不平衡感，因此迅速成为景观桥梁界的宠儿。与传统样式的拱桥相比，该桥的力学行为与传力途径有所不同，而吊杆作为传力途径中最重要也最易受损的构件，其健康状况是整座桥梁能否安全运营的基础[2-4]，因此对吊杆损伤后桥梁动力特性的研究至关重要。

目前，国内很多学者针对不同拱或斜拉桥的吊杆损伤进行了一系列的研究，例如：葛素娟等[5]研究发现了下承式拱桥的稳定性受吊杆损伤的影响；孙全胜等[6]分析了无背索斜拉桥自振特性受拉索损伤的影响；陈淮及陈景星等人[7-8]研究分析了钢管混凝土拱桥的动力特性受吊杆损伤的影响。以上学者的研究大多是针对传统线形的拱桥或斜拉桥，而对于结构体系较纤柔的外倾单肋式曲线钢拱桥吊杆损伤的研究尚未见报道。

本文以某外倾单肋下承式人行曲线钢拱桥为背景，探讨了吊杆损伤对此类异形钢拱桥动力特性的影响，该结果对同类型桥梁具有一定的借鉴意义。

1 工程概况

1.1 桥梁概况

该桥为跨径12.5 m+105 m+12.5 m的三跨外倾单肋式异形下承式人行钢拱桥，中跨和两边跨主梁以跨中为对称中心位于平曲线上，桥梁布置如图1、图2所示。拱肋向外倾斜15°，拱轴线在拱肋倾斜面内为二次抛物线，矢高为26.25 m，矢跨比为1∶4。拱肋截面为矩形变截面，其拱脚特征断面尺寸如图3所示。为增加拱肋刚度，在拱肋拱脚截面以上6 m范围内灌入标号为C40的微膨胀混凝土。吊杆采用强度为1 860 MPa、规格为5φs15.2的钢绞线，其间距为4.5 m，全桥共19根吊杆。主梁截面为宽5 m的非对称单箱双室钢箱，其标准截面如图4所示。两端支撑在桥台上，距梁端12.5 m处通过钢横梁与拱肋连接，如图5所示。

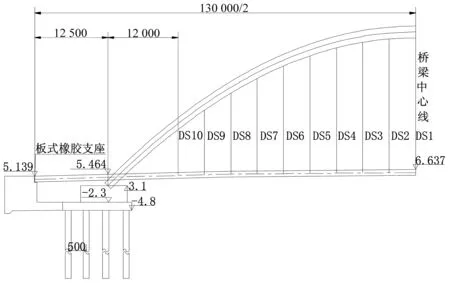
图1 桥梁立面图(单位:mm)

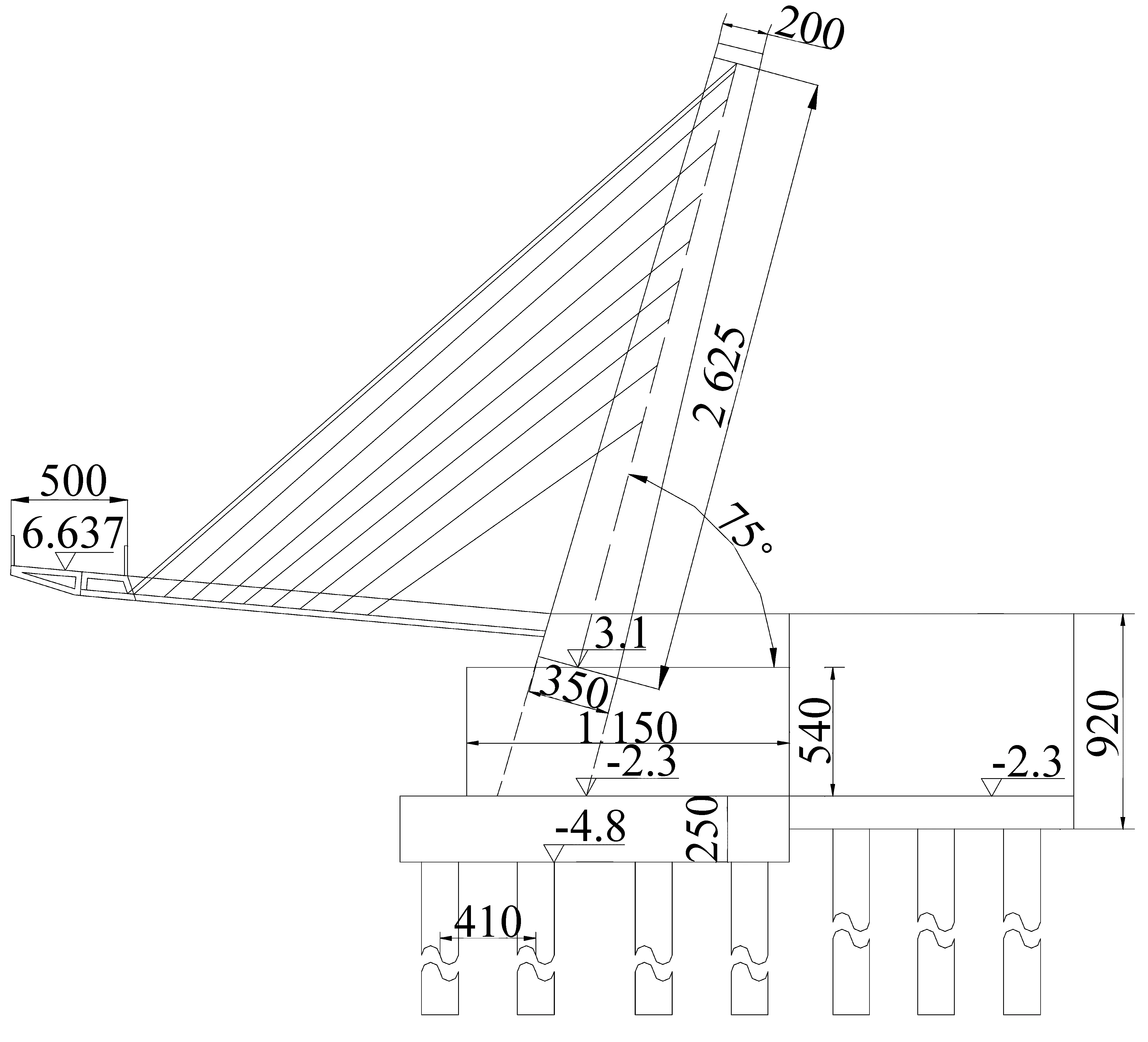
图2 桥梁横断面图(单位:mm)

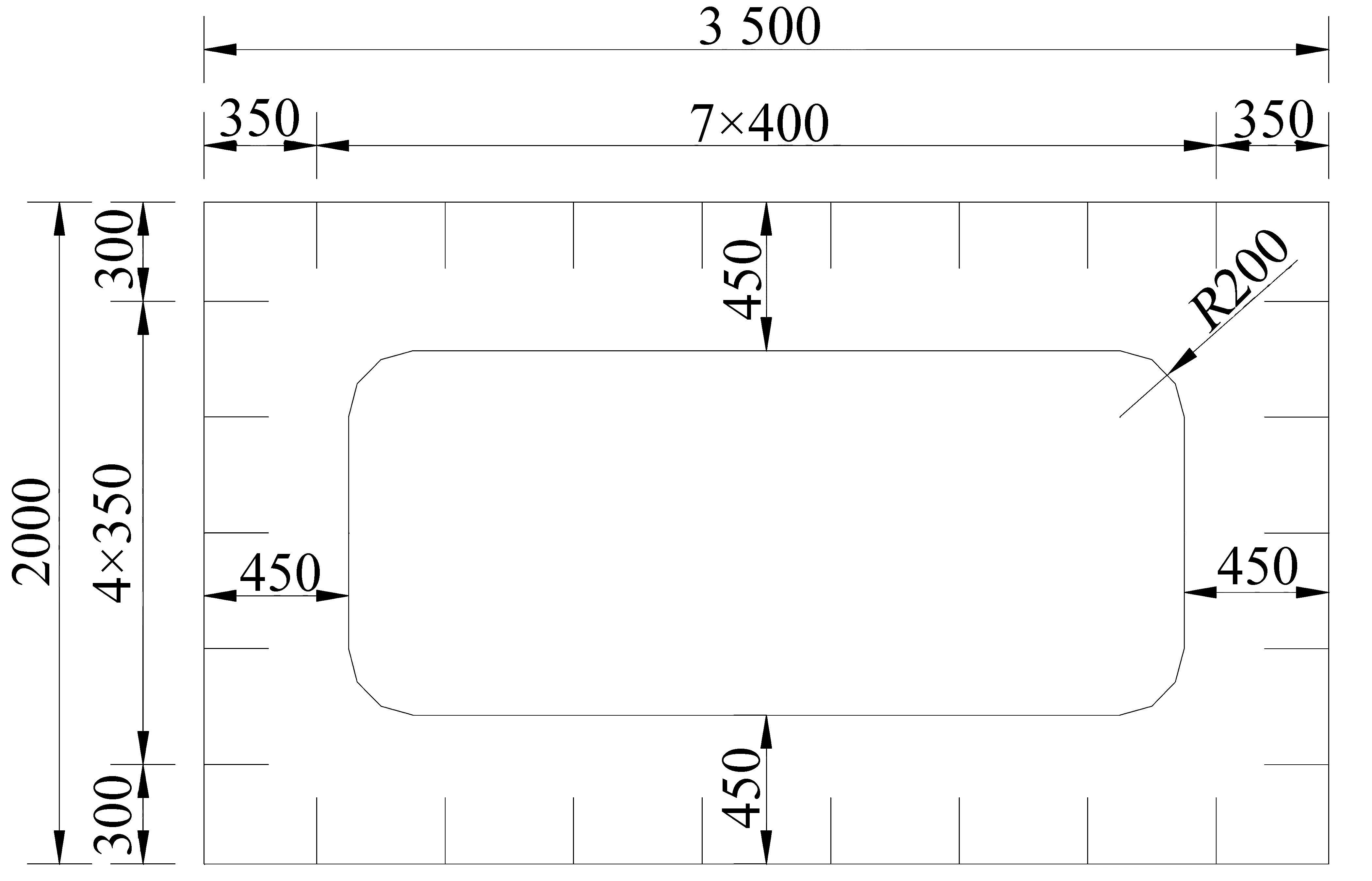
图3 拱脚特征断面(单位:mm)

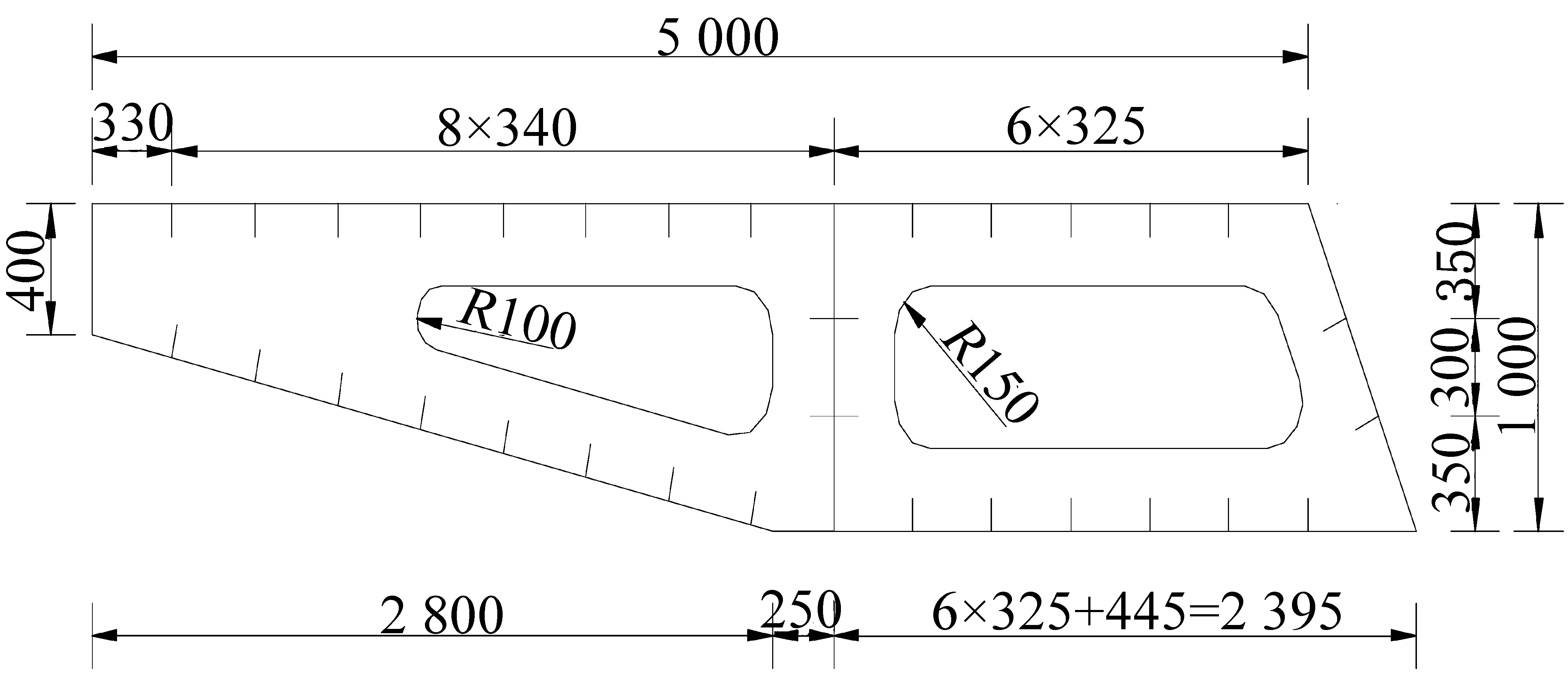
图4 主梁断面图(单位:mm)

1.2 结构分析计算模型

有限元软件Midas/Civil所建立的三维模型见图5所示，全桥共划分364个节点，383个单元，拱肋、主梁及横梁均采用梁单元模拟，吊杆采用桁架单元模拟。梁端采用一般支承，仅设置竖向约束，拱脚完全固结。本次模型分析选用对于求解结构低阶数特征值效率较高的子空间迭代法，特征值控制参数分别为：迭代次数100，子空间大小1，收敛误差1e-10。

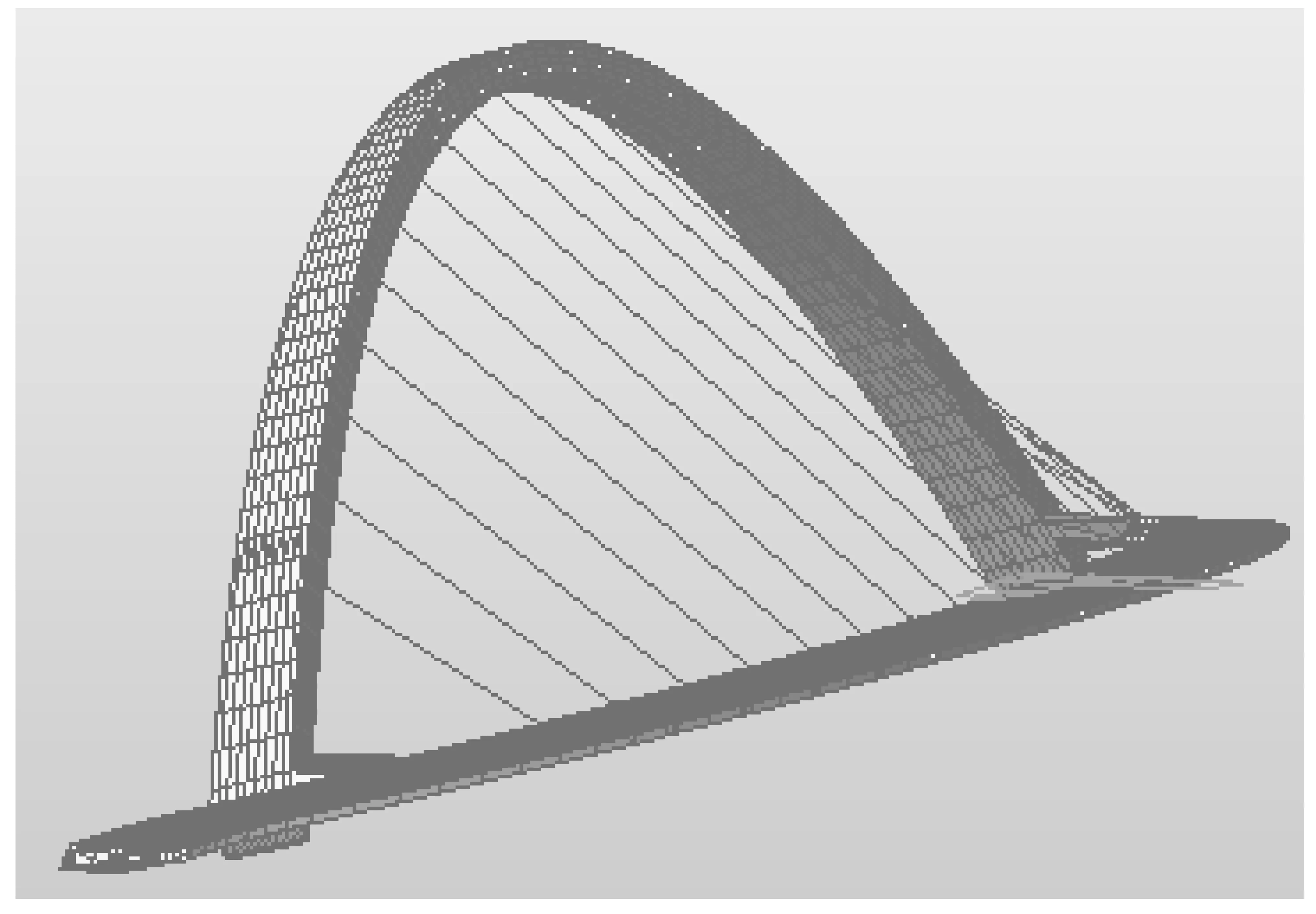
图5 桥梁有限元模型

2 吊杆损伤程度的确定

实际工程中吊杆损伤的本质是吊杆张力的下降或丧失，目前主要采用面积折减、弹模折减、反向荷载和实体单元等方法对吊杆损伤进行模拟[9]，其中弹模折减模拟吊杆损伤程度的方法简便易懂，是较为常用的一种方法。

由于全部吊杆或部分吊杆同时发生损伤的概率较低，单根吊杆出现损伤的概率最大，因此本文采用降低单一吊杆弹性模量的方法对其损伤程度进行模拟分析，得出吊杆损伤程度对该异形钢拱桥动力特性的影响。由于桥梁属于对称结构，故文中只计算了以下41种吊杆损伤工况下的桥梁自振特性。

工况1—10：DS10—DS1号吊杆损伤25%；

工况11—20：DS10—DS1号吊杆损伤50%；

工况21—30：DS10—DS1号吊杆损伤75%；

工况31—40：DS10—DS1号吊杆完全断裂；

工况41：所有吊杆完好。

结构动力特性中的自振频率和振型是对结构进行动力分析的重要参数。对于所研究的多次超静定、动力自由度较多的异形桥梁来说，求解其全部自振频率较为困难，故文中仅给出其起控制作用的前若干阶频率及其对应的振型。

3 桥梁自振特性分析

对桥梁初始状态(即工况41所有吊杆完好)进行模态分析，求解其自振特征，所得结果的前5阶振型图如图6所示。前10阶自振频率及振型特征如表1所示。

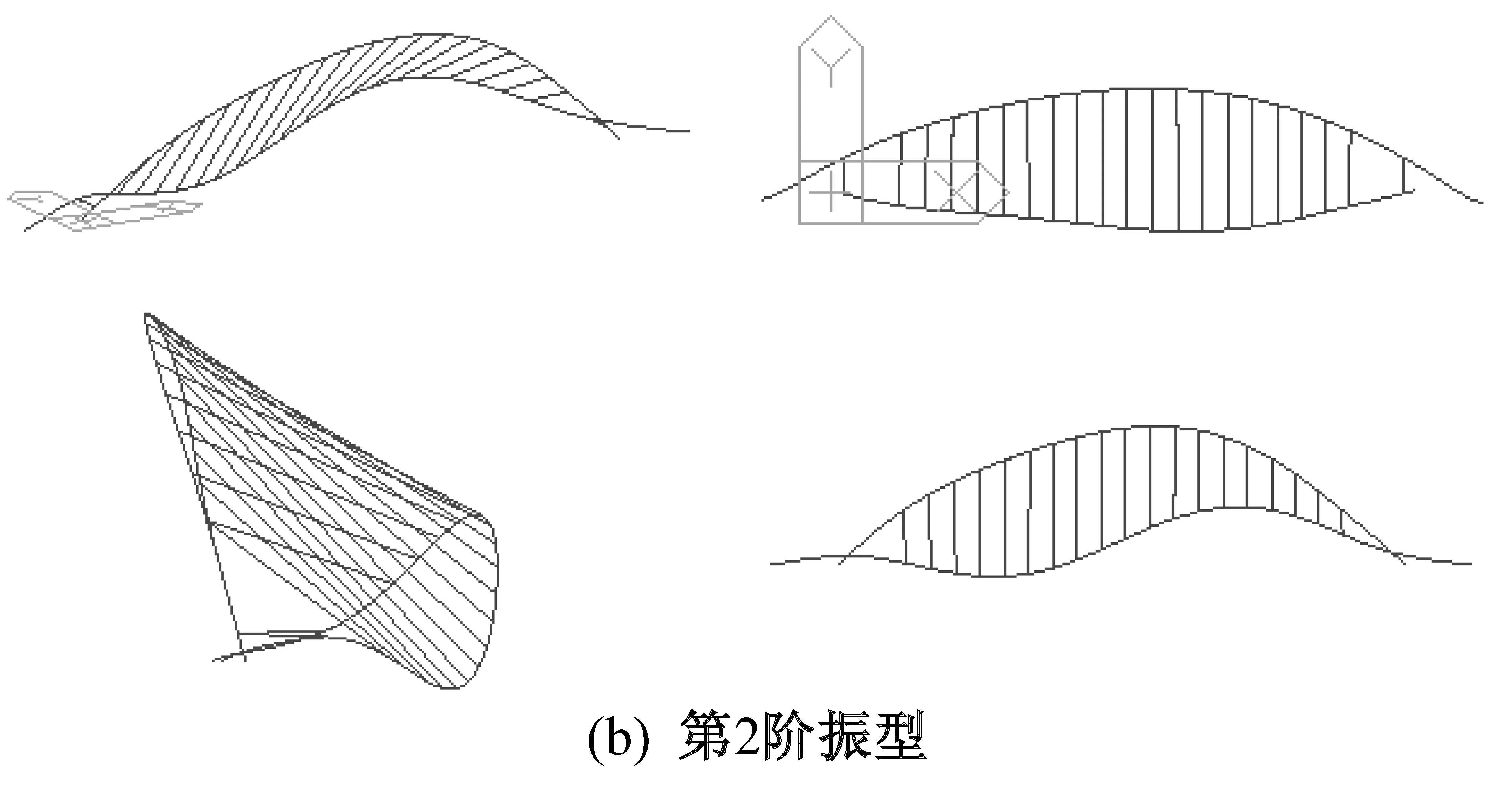
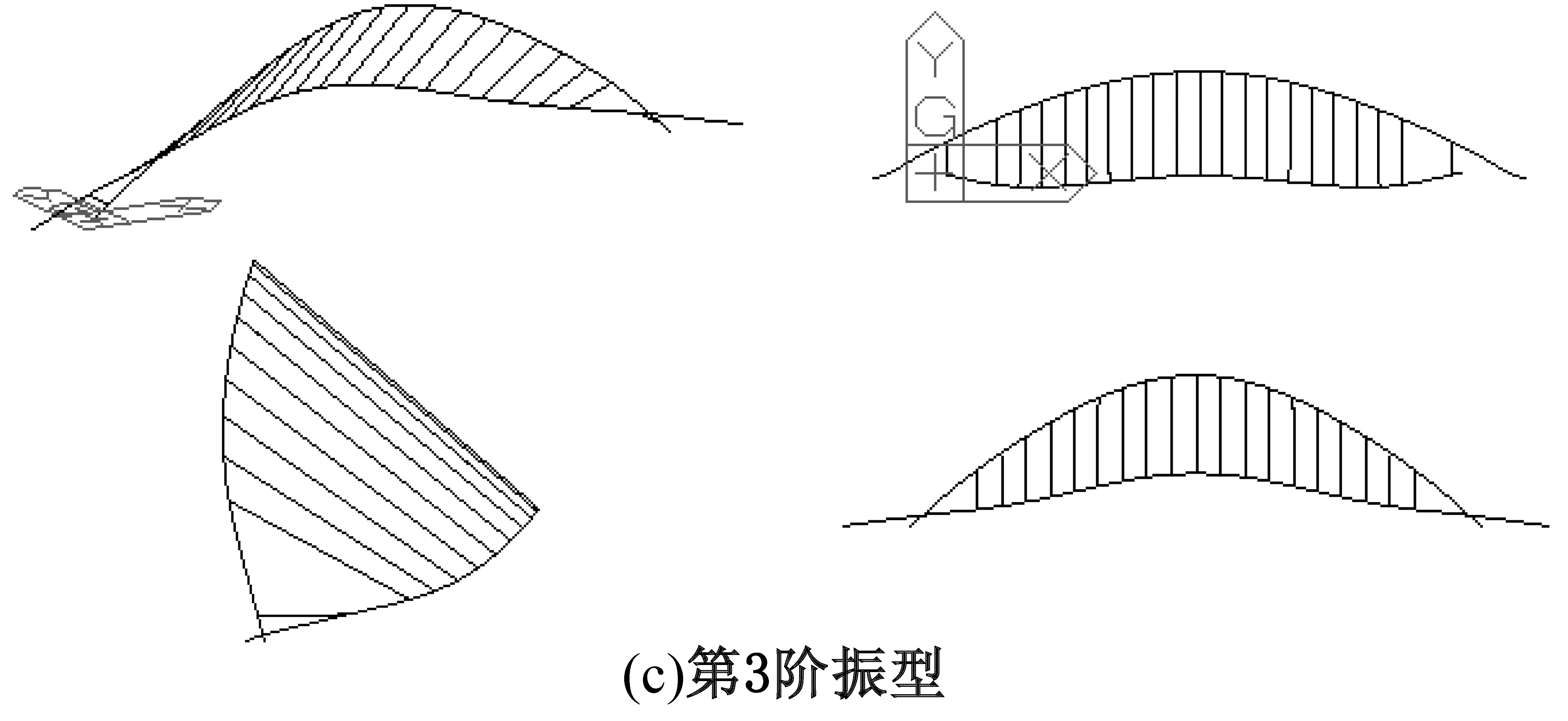
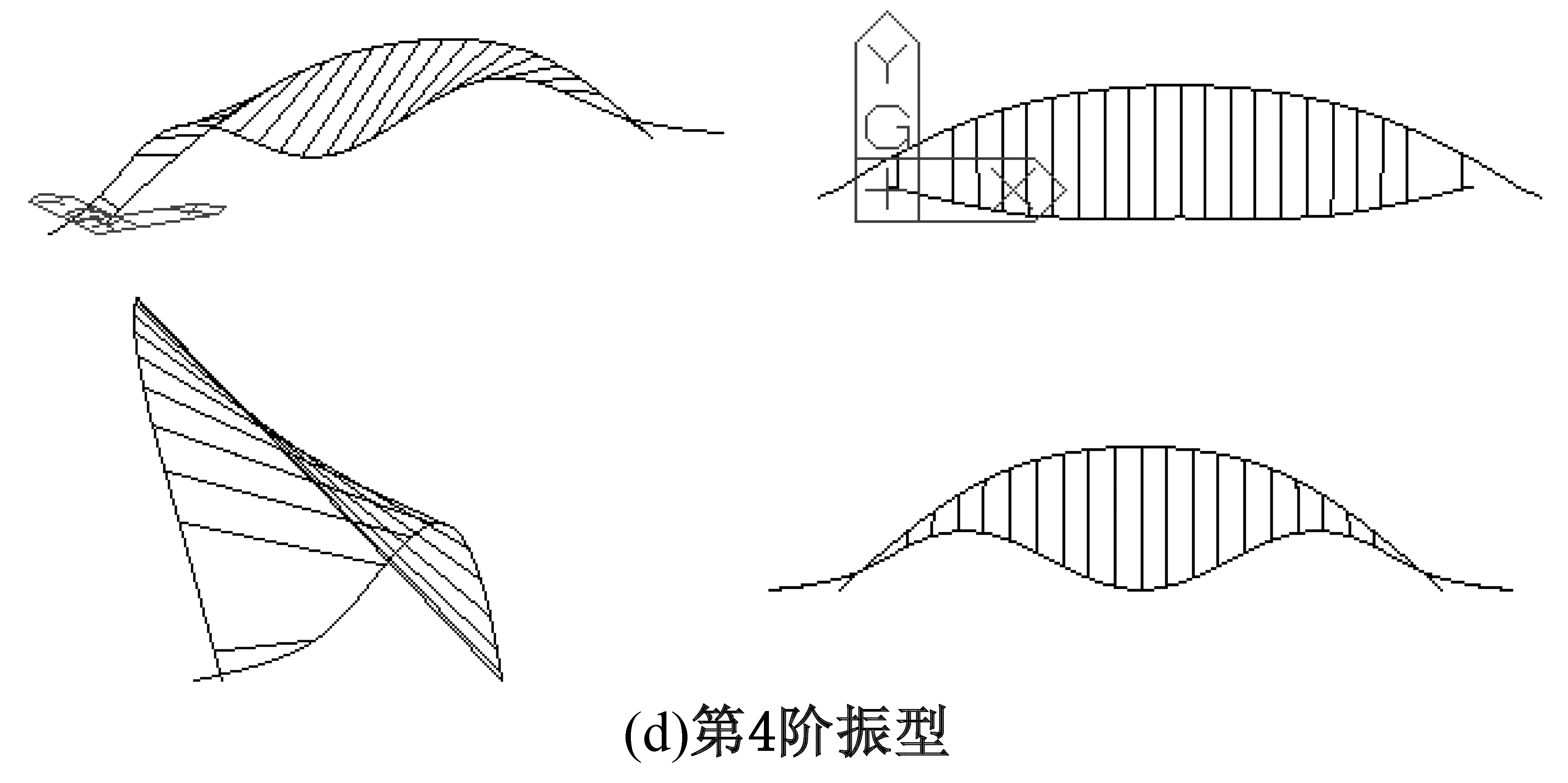
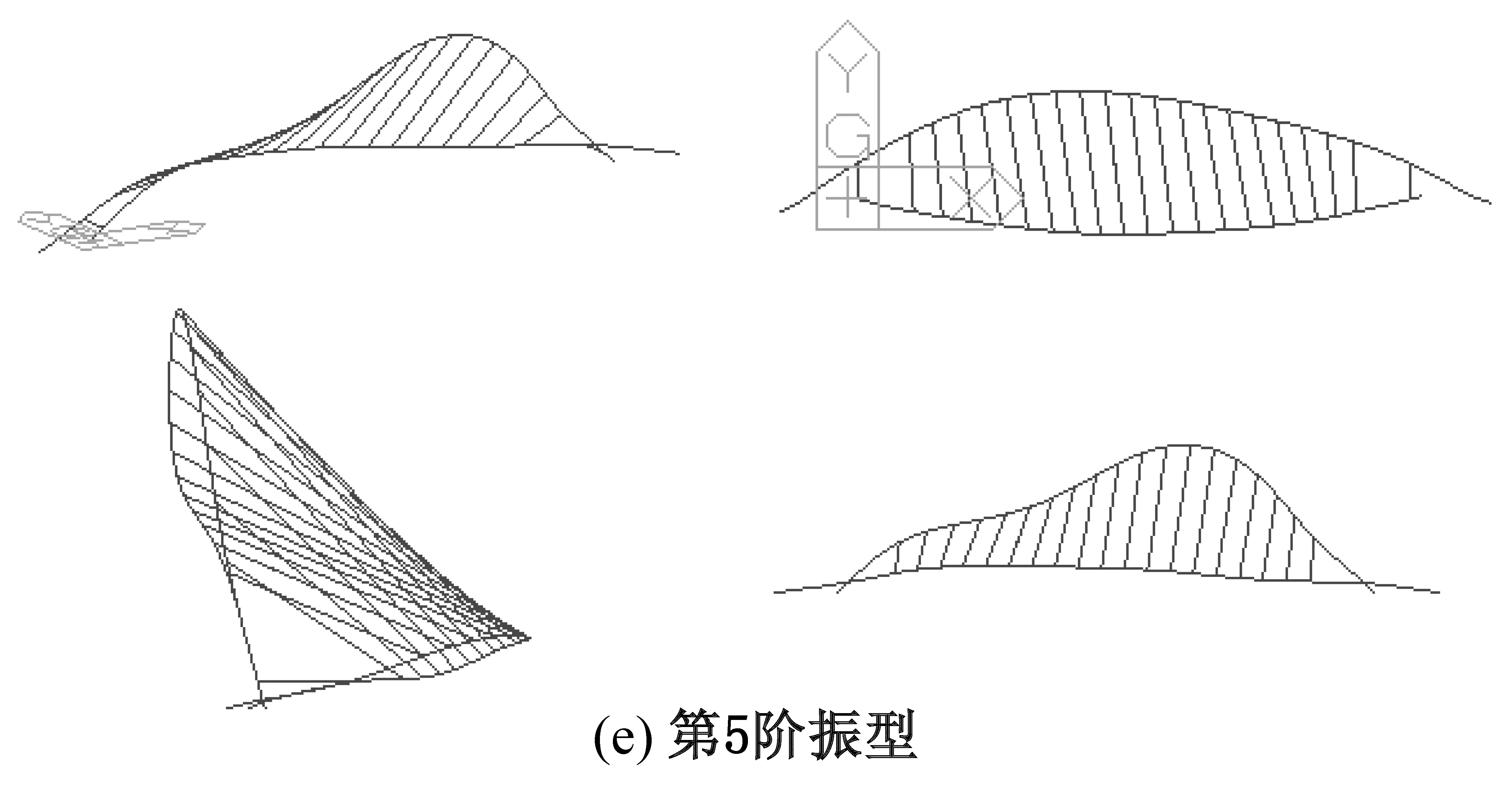
图6 模型前5阶振型

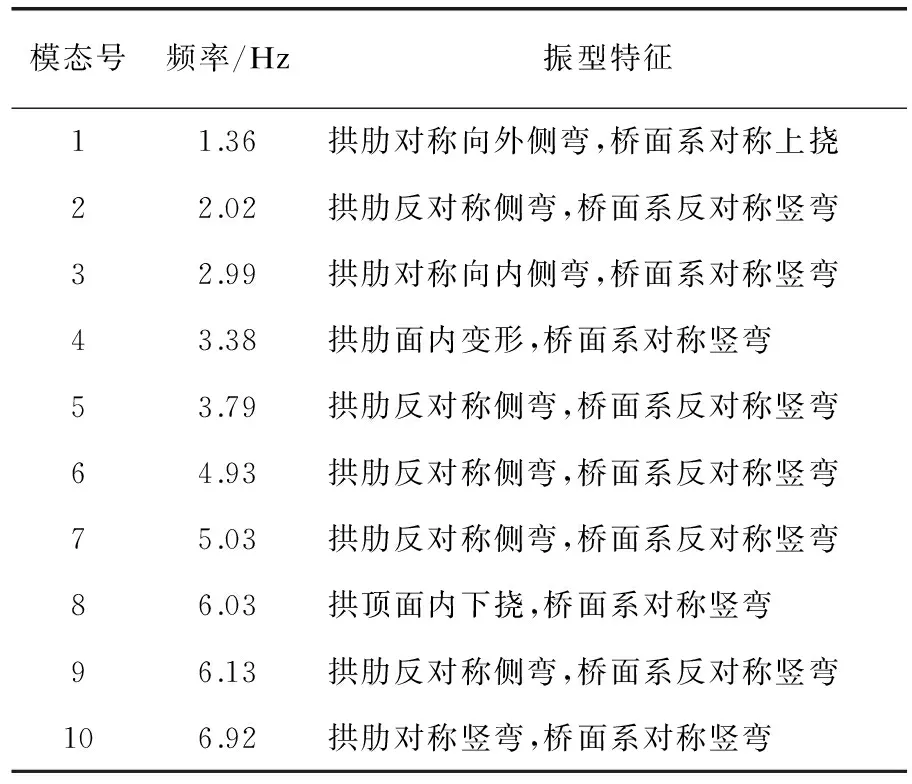
模态号频率/Hz振型特征11.36拱肋对称向外侧弯,桥面系对称上挠22.02拱肋反对称侧弯,桥面系反对称竖弯32.99拱肋对称向内侧弯,桥面系对称竖弯43.38拱肋面内变形,桥面系对称竖弯53.79拱肋反对称侧弯,桥面系反对称竖弯64.93拱肋反对称侧弯,桥面系反对称竖弯75.03拱肋反对称侧弯,桥面系反对称竖弯86.03拱顶面内下挠,桥面系对称竖弯96.13拱肋反对称侧弯,桥面系反对称竖弯106.92拱肋对称竖弯,桥面系对称竖弯

由图6和表1可看出，该异形钢拱桥的前10阶振型主要有拱肋的外倾和面内变形，桥面系的对称或反对称竖弯。

模拟所得的结构1阶自振频率为1.36 Hz，但该频率值小于《城市人行天桥与地道技术规范》(CJJ 69—95)[10]中人行桥结构竖向自振频率3 Hz规定，降低了桥上行人的舒适感，因此，对此类柔性桥梁的动力特性更应重视。

4 自振特性计算结果及分析

为了准确比较吊杆损伤对异形拱桥动力特性的影响，从不同吊杆相同的损伤程度和同一吊杆不同的损伤程度两种情况进行分析，对比吊杆损伤对异形拱桥自振特性的影响。

4.1 不同吊杆相同损伤程度

文中仅计算了编号为DS2、DS4、DS6、DS8和DS10的5个吊杆在弹模分别损伤25%、50%、75%及100%(即断裂)程度后的桥梁自振频率，图7—10分别给出了5根吊杆同一损伤程度下的桥梁自振频率变幅情况，其自振频率变幅=(吊杆损伤后频率-完好状态自振频率)/完好状态自振频率。

由图7—10可以看出，不论哪根吊杆出现损伤都会导致桥梁自振频率下降，对比其曲线变化可知，吊杆损伤程度越大，结构的自振频率降低幅度越大，吊杆损伤情况下，结构的自振频率随振型阶数的增加呈锯齿形规律变化。

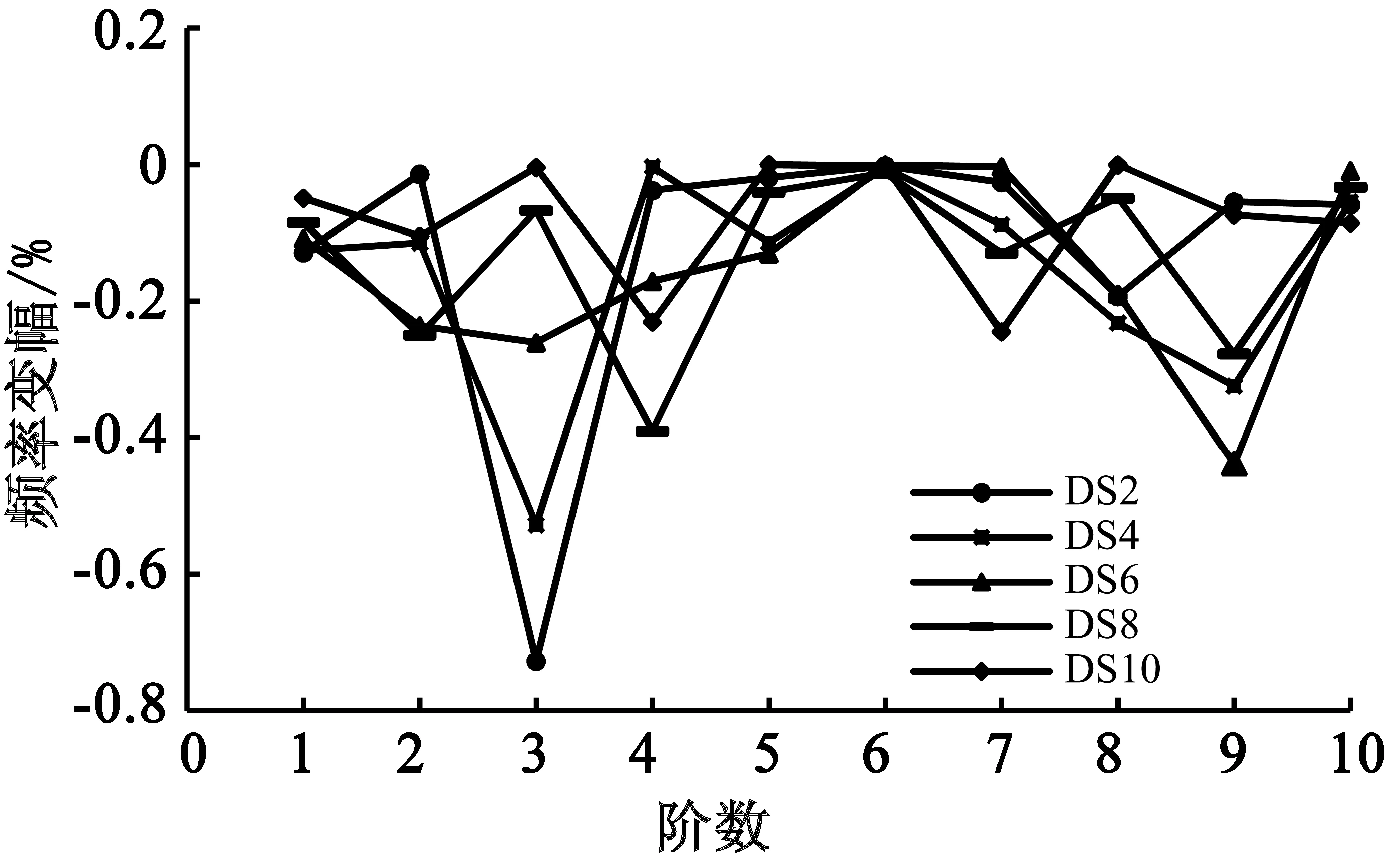
图7 吊杆损伤25%

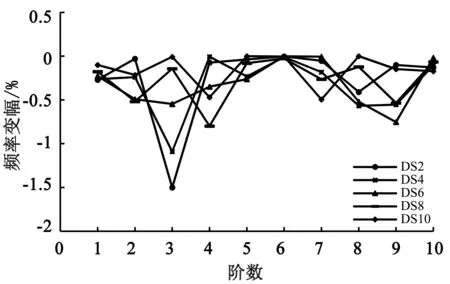
图8 吊杆损伤50%

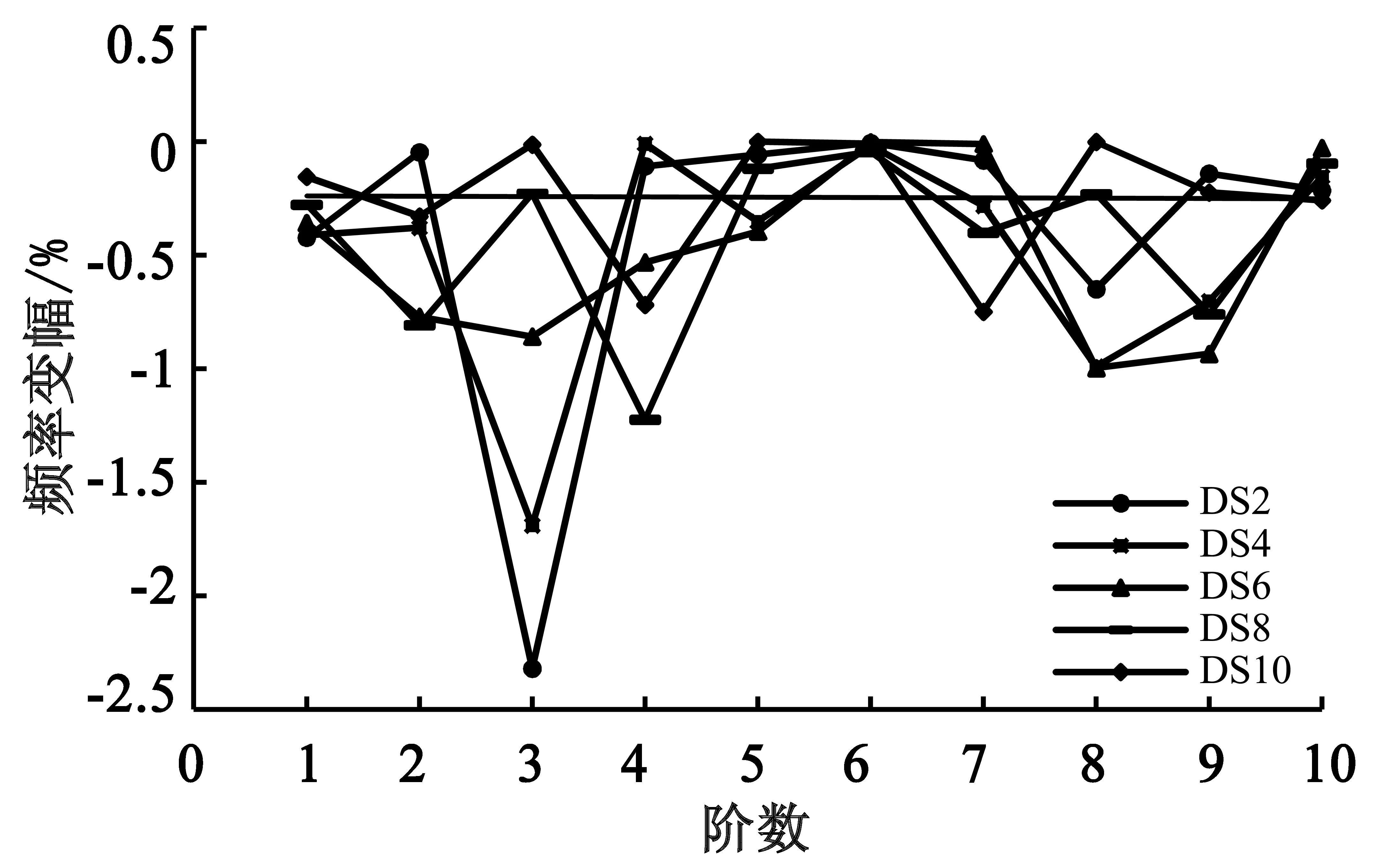
图9 吊杆损伤75%

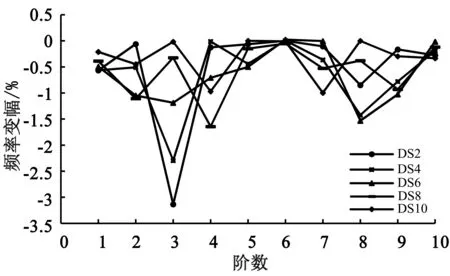
图10 吊杆断裂

吊杆损伤程度由25%到吊杆断裂(损伤100%)时，DS2号吊杆损伤引起的结构第3阶自振频率降幅最大，分别为0.73%、1.5%、2.3%和3.13%；DS4号吊杆损伤引起的结构自振频率降幅最大值也出现在第3阶，分别为0.53%、1.1%、1.7%和2.3%；DS8号吊杆损伤引起的结构第4阶自振频率降幅最大，分别为0.39%、0.80%、1.22%和1.64%；DS10号吊杆损伤引起第7阶自振频率降幅最大，为0.24%、0.49%、0.75%和1.0%。DS6号吊杆损伤程度为25%和50%时，自振频率降幅最大出现在第9阶，为0.44%和0.75%；损伤程度为75%和100%时，自振频率降幅最大出现在第8阶，为1.0%和1.5%。

对比DS2、DS4、DS6、DS8和DS10吊杆相同损伤程度引起的频率变幅可知，相同的吊杆损伤程度下靠近跨中的吊杆对结构自振频率影响较大。

4.2 同一吊杆不同损伤程度

为研究同一吊杆不同的损伤程度对桥梁自振频率的影响，同样取25%、50%、75%和100%(断裂)4种损伤程度对桥梁自振特性进行分析。图11—15给出了编号为DS1、DS3、DS5、DS7和DS9的5根吊杆在不同损伤程度后桥梁自振频率变幅图。

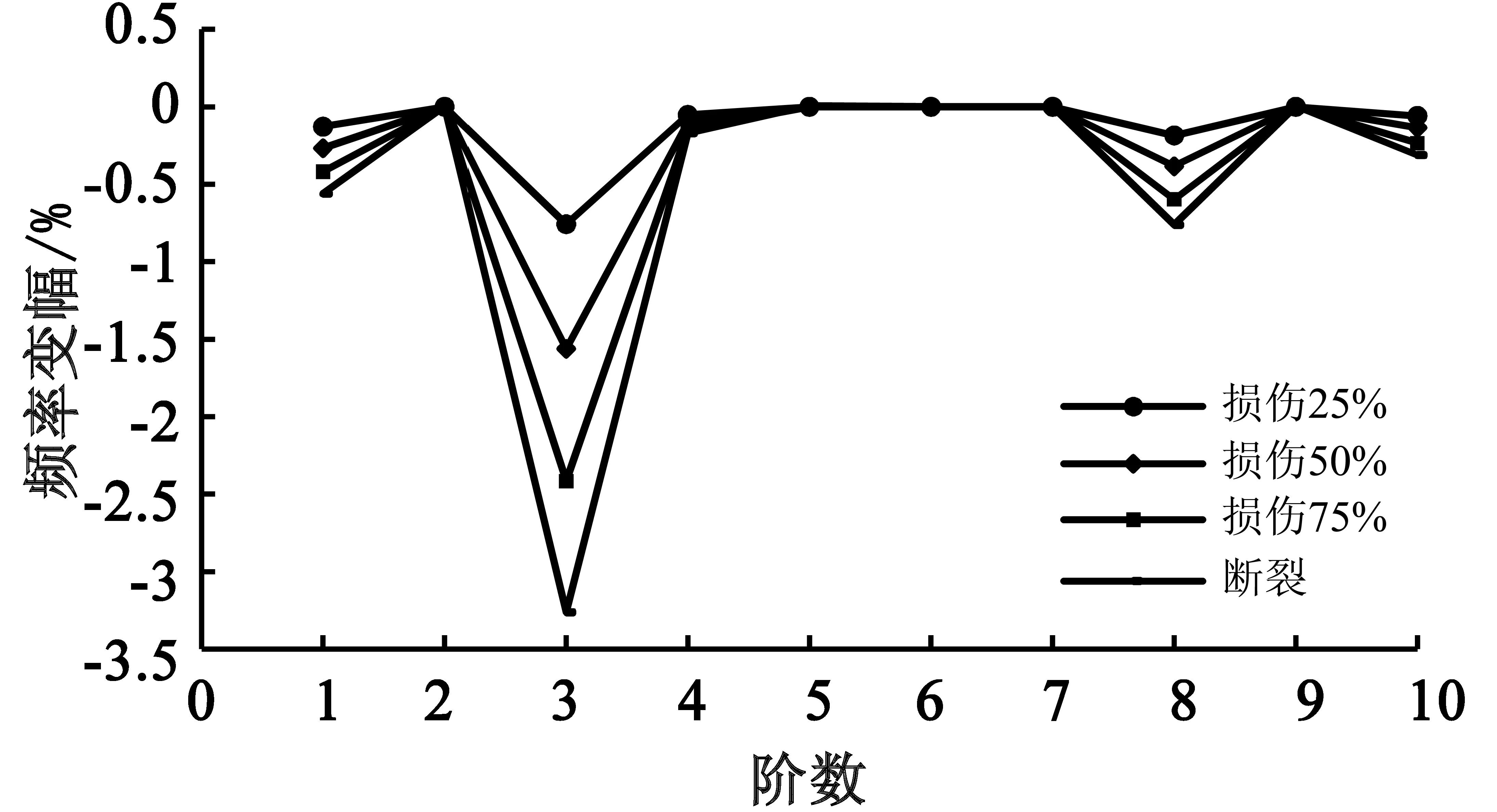
图11 DS1损伤

图12 DS3损伤

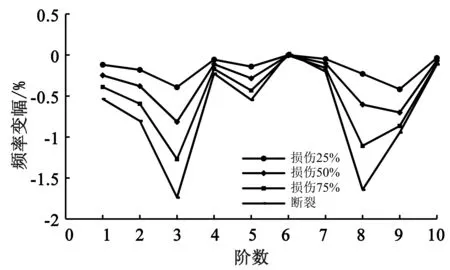
图13 DS5损伤

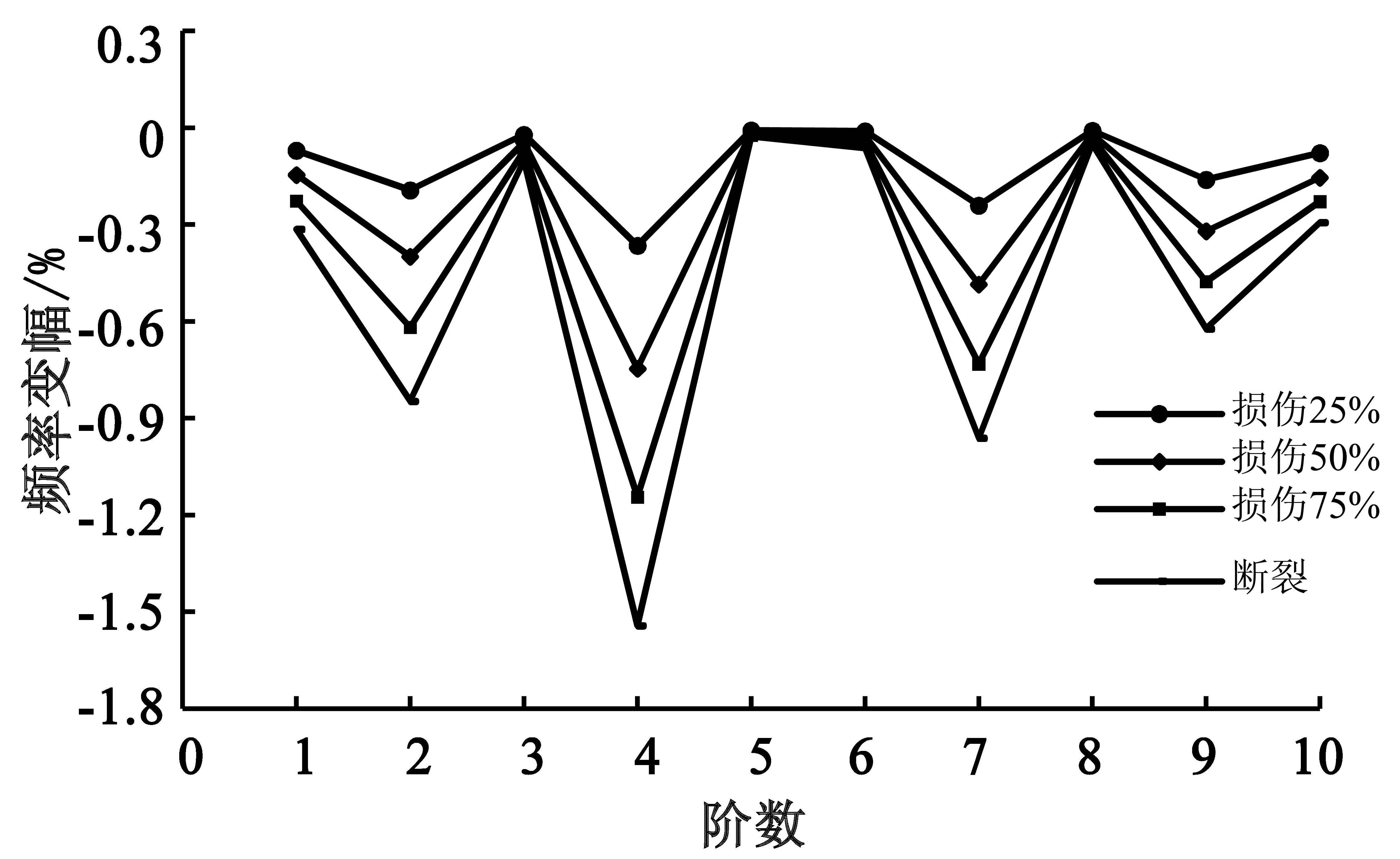
图15 DS9损伤

由图11和图12频率变幅规律可知，DS1和DS3吊杆损伤对拱桥的自振频率影响主要集中在低阶频率。吊杆损伤对结构第3阶自振频率的影响最大，在4种损伤情况下，DS1的第3阶频率变幅分别为0.76%、1.56%、2.42%、3.26%，DS3的第3阶频率变幅分别为0.65%、1.33%、2.06%、2.79%；损伤对其他阶次自振频率的的影响较小，甚至为0。

由图13—15可知，DS5、DS7和DS9吊杆损伤对结构不同阶次的自振频率均有一定程度的影响。其中DS5吊杆不同程度损伤对第3阶自振频率的影响最大，为0.39%、0.82%、1.27%和1.74%；DS7和DS9号吊杆不同程度损伤对结构第4阶自振频率的影响程度最大，分别为0.31%、0.63%、0.96%、1.28%和0.36%、0.75%、1.14%、1.54%。

由DS1、DS3、DS5、DS7和DS9吊杆频率变幅可知，同一吊杆随着吊杆损伤程度的增加，其结构的自振频率降幅增大。

5 结论

1)吊杆是拱桥中重要的传力构件，作为传力途径中最重要也最易受损的构件，其健康状况是整座桥梁能否安全运营的基础。

2)吊杆损伤，结构的自振频率均降低，且损伤程度越高自振频率的降幅越大。

3)DS1和DS2吊杆断裂时引起的自振频率降幅较大，分别为3.26%和3.13%，但其对高阶频率的影响很小，甚至为0。

4)吊杆损伤对该桥高阶自振频率影响较小，对低阶尤其是第3阶自振频率影响较大。

5)不同吊杆发生相同程度损伤时，自振频率的降幅呈锯齿形变化规律。

[参考文献]

[1] 王玮瑶，李生智，陈科昌.异型系杆拱桥[J].中国公路学报，1996，9(1)：45-50.

[2] 夏欢，金晓勤，晏班夫.拱桥在役损伤吊杆破断安全性研究[J].中外公路，2017，37(1)：89-93.

[3] 吴文清，余江昱.系杆拱桥吊杆的破损安全设计方法研究[J].桥梁建设，2016，46(1)：35-39.

[4] 何伟，何容，陈淮.运用中、下承式拱桥吊杆张力变化进行吊杆损伤识别研究[J].振动与冲击，2012，31(5)：153-157.

[5] 葛素娟，陈淮.考虑吊杆损伤的拱桥稳定性分析[J].世界桥梁，2006(3)：38-41.

[6] 孙全胜，张可心.拉索损伤对无背索斜拉桥自振特性影响分析[J].中外公路，2016，36(1)：144-148.

[7] 陈淮，葛素娟.吊杆损伤对钢管混凝土拱桥自振特性影响的分析[J].桥梁建设，2008(4)：24-26.

[8] 陈景星，冯忠居，胡锋.吊杆损伤对钢管混凝土拱桥动力特性的影响[J].公路交通科技，2013，30(3)：100-104.

[9] 葛俊颖，苏木标.斜拉桥拉索损失模拟方法及其对索力和挠度分布规律的影响[J].中国铁道科学，2016，37(3)：30-37.

[10] 中华人民共和国交通部.城市人行天桥与人行地道技术规范：CJJ 69—95[S].北京：人民交通出版社，1995.