中职高考数学研究之集合论

王斌

摘要：集合论是中职高考数学的开始部分，也是高考的重要组成部分，对集合的发展和考点的了解，知识点的理解及典型题解题思路、解题方法的把握无论对学习者还是教育者都很重要，在此把个人研究所得分享给大家。

关键词：集合 集合运算 题型 解题思路

中职高考中，无论是从高考的分值上看，还是从数学的学科特点上看，数学都是重中之重的学科，集合论是中职数学高考的第一部分内容，良好的开端等于成功的半，所以学习好集合，对中职数学的学习和高考的良好成绩，有着至关重要的作用。本人对这部分知识加以研究，把自己的研究所得分享给各位。

一、集合论的发展

集合论的创始人是法国数学家康托尔（GeorgCantor，1845—1918），集合论的产生不仅是数学发展史上的一座里程碑，也是人类思维发展史上的一座高耸的里程碑，它使人类的認识从有限到无限，对无限的性质有了初步的了解，实现了从对有限的研究到对无限的研究的巨大飞跃。被誉为“数学思想最惊人的产物，在纯粹的理性范畴中人类活动最美的表现之一”。然而，1903的英国哲学家、数学家罗素（Russell.B.A.W，1872—1980）提出一个悖论“一切不包含自身的集合所形成的集合是否包含自身？”并通俗地给出了“理发师悖论”、“语义学悖论”，戏剧性地把集合论推下断崖，从而产生数学发展史上“第三次危机”。后来，E.F.F策梅洛各A.A弗伦克尔的ZF系统，实现了朴素集合论到公理集合论转化，解决了集合论的矛盾，形成了现代数学的一个重要分支——集合论，在数学研究、数学应用起着重要的作用。

二、集合论的主要知识点

中职数学所涉及的集合论中主要的知识结构是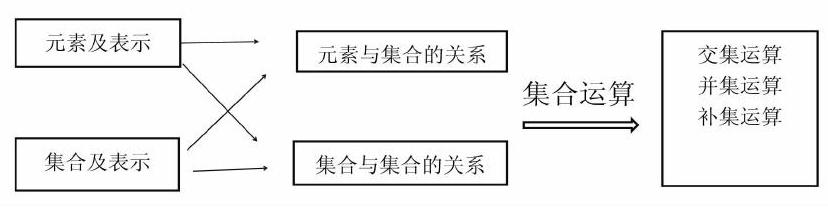

集合的学习过程与数字的学习过程很相似，都是先认识，后进行运算，所以，在学习过程中，可以利用类推的方法进行，同时，也要注意不同，理清每一个知识点的内容，如，元素及表示知识点，有元素的定义、还有用小写字母表示元素，还有一些特定字母表示特定的数集；集合及表示知识点，既有集合的定义、用大写字母表示集合，还有集合的表示方法，列举法、描述法。集合与集合的关系中，强化一个集合中有n个元素，求它的子集的个数（2n ），真子集的个数（2n-1），非空真子集的个数（2n-2），也就强化了集合之间的关系了。集合的交、并、补运算首先要把握定义，真正理解交、并、补运算，然后通过典型题型运算步骤，做题训练，达到对交、并、补运算的进一步理解。

三、典型考题解析

（一）集合的交运算有三种题型，下面分别列举解析一下

解析：这类题也是在数轴上画图，分别在数轴上画出集合A、B的范围，根据补集的定义，集合B在集合A中的补集就是集合A的范围去掉集合B的范围剩下的部分组成的集合。值得注意的是，初学者对端点的归属很容易出错，应仔细思考。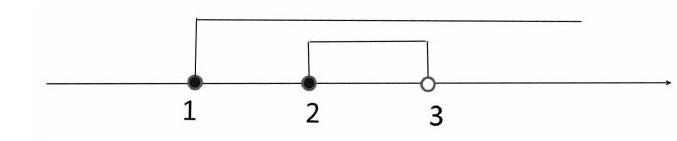

集合这部分内容，在历年中职高考中，第一小题都是集合问题，范围也不超出以上的几种题型，第一大题惯例是求函数定义域，也涉及到集合及集合运算，也不超出以上几种题型，所以无论是教授集合论还是学习集合论都应该好好把握以上内容，在此整理出来，分享给大家。

参考文献：

[1]李广全.数学（基础模块）[M].高等教育出版社，2013.

[2]教育部.教师专业化的理论与实践[M].人民教育出版社，2001.

（作者单位：辽宁省丹东市文化艺术学校）