基于线圈磁耦合模型的无线充电仿真研究*

丁云广， 闵昌万

(空间物理重点实验室， 北京 100076)

目前， 在物联网领域， 主要的能量供给方式为电池或有线供电. 在密闭狭小的空间内， 由于安装有众多的电子设备， 采用电池供电方式会造成能量的二次补给困难、 采用有线方式会带来走线困难的问题.对于物联网节点这种超低功耗的负载， 使用有线供电的方式对于飞行器结构减重也有不利影响.

2007年7月麻省理工学院以Marin Soljacic教授为首的研究小组在《Science》上发表论文[1], 他们发现了一种全新的无线供电模式——非辐射电磁能谐振隧道效应， 称作“WiTricity(Wireless electricity transfer)”技术， 也称为磁共振感应耦合技术. 此后， Intel公司、 斯坦福大学、 Powermat公司、 SONY公司、 日本东京大学、 卡内基梅隆大学都对该技术进行了深入开发[2-8].

基于磁耦合模型的无线电能传输技术被提出用于解决物联网节点的供电问题， 目前对于磁耦合模型的无线电能传输技术的研究工作很多学者都有开展， 在实际应用中大多为大线圈正对的传输方式， 传输的能量较大， 本文所要解决的是在狭小空间内使用小线圈传输能量， 用于满足超低功耗负载的应用.

1　磁耦合无线电能传输模型

无线电能传输系统在实现了电能无线传递的同时， 其传输效率受到多个因素的制约， 整体的工作效率是绕组结构、 耦合效果、 工作频率和驱动模式等共同作用的结果， 而传输距离的增减也会直接影响传输效率[9]. 对于本文设计的磁耦合谐振式无线电能传输模型的关键在于电磁发射系统和电磁接收系统， 其模型如图 1 所示.

图 1　电磁耦合系统模型Fig.1　Electromagnetic coupling system model

图 2　负载终端等效电路Fig.2　Terminal load equivalent circuit

考虑负载绕组对振荡器品质因素的影响时， 可将振荡器a2及负载视为一个由两者组合而成的新振荡器[10]， 等效电路如图 2 所示.

此时忽略负载电阻RD， 并保证电路工作在同一角频率ω， 则负载所获得的有功功率

(1)

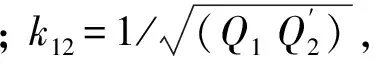
图 3　发射绕组与接收绕组示意图Fig.3　A schematic diagram of the transmitting and receiving windings

针对同轴放置的绕组， 如图 3 分析无线电能传输系统的轴向距离特性， 在发射绕组与接收绕组为同轴螺旋线圈时， 在准静态条件r=D下， 谐振耦合式无线电能传输距离与互感的关系为[11]

M=M12=M21=πμ0(n1n2)0.5(r1r2)2/2D3,

(2)

式中：n1,n2为发射与接收线圈绕组的匝数；r1,r2为发射与接收线圈绕组的半径；D为线圈间的距离. 对于结构、 参数相同的发射绕组：n1=n2=n，r1=r2=r, 则得到

M=πμ0nr4/2D3.

(3)

高频条件下绕组的损耗电阻

(4)

式中：ω为角频率；σ为电导率；a为线径.

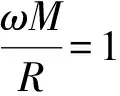
(5)

由式(5)可知： 有效传输距离D与绕组半径r、 线径a、 角频率ω、 电导率σ等因素有关.

至此， 基于等效电路的磁耦合基本理论模型建立完成.

2　磁耦合无线电能传输仿真分析

对于磁耦合无线电能传输的仿真分析是设计良好的无线电能传输模块的必要环节. 本文仿真分析的物理基础为： 发射绕组电源激励为28 V； 负载用电需求电压为5 V, 电流为100 mA； 使用MAXWELL仿真， 分别得到了实际环境容许使用的频率范围条件下， 不同频率、 不同幅值下的无线电能传输能力的结果.

建立如图 4 所示的仿真正对线圈模型： 两个外径6 cm， 内径1 cm的正对线圈间距为10 cm.

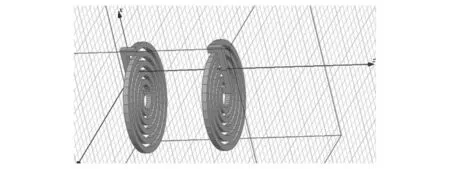
图 4　建立仿真正对线圈模型Fig.4　Establishment of a simulation model of positive pair of coils

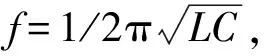
图 5　谐振电路Fig.5　Resonant circuit

振荡频率为500 kHz， 幅值1 A时的仿真结果如图 6 所示； 振荡频率为500 kHz， 幅值为10 A时仿真结果如图 7 所示； 振荡频率为1 000 kHz， 幅值为1 A时的仿真结果如图 8 所示.

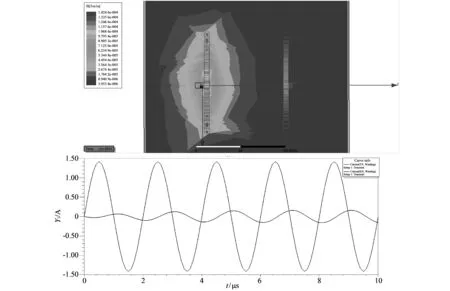
图 6　500 kHz, 1 A的场强分布与输入输出电流Fig.6　Field intensity distribution and input and output current of 500 kHz and 1 A

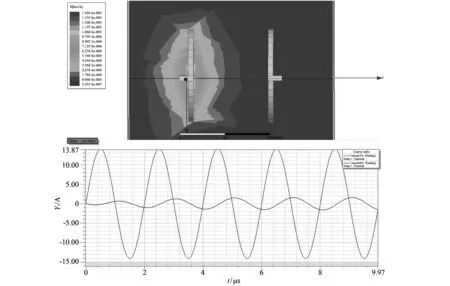
图 7　500 kHz, 10 A的场强分布与输入输出电流Fig.7　Field intensity distribution and input and output current of 500 kHz and 10 A

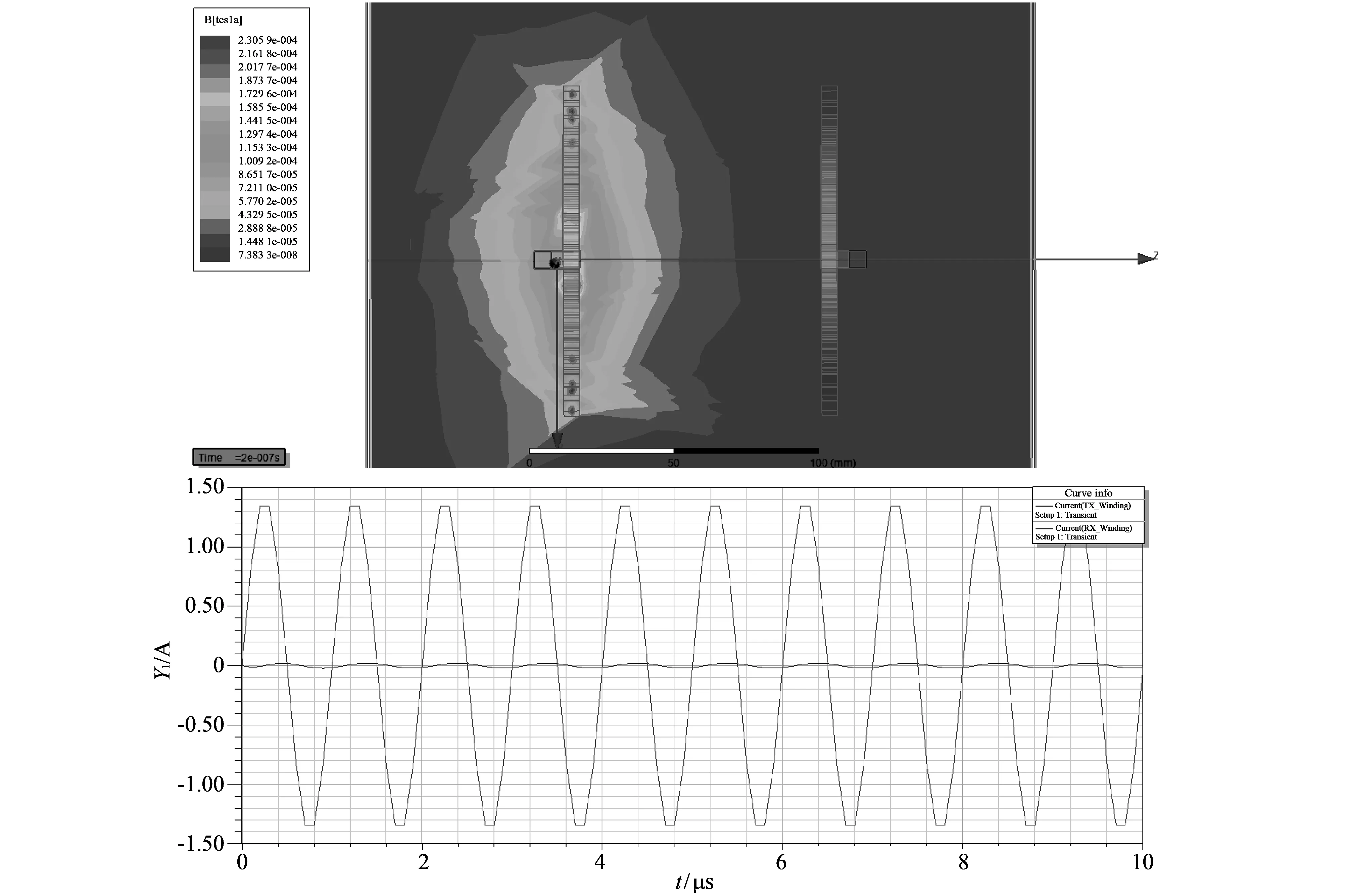
图 8　1 000 kHz, 1 A的场强分布与输入输出电流Fig.8　Field intensity distribution and input and output current of 1000 kHz and 1 A

由仿真结果可知， 在500 kHz, 1 A幅值与1 000 kHz, 1 A幅值时都可以满足系统设计要求， 考虑对其余单机的影响， 选择500 kHz更加贴合设计需求， 由仿真结果可知： 谐振频率在一定范围内的提高有助于提高传输效率， 超过一定频率后传输效率下降.

3　结束语

国内很多学者对无线电能传输技术的电磁辐射、 电磁兼容以及产品推广中的标准也都进行了研究[12-15]， 本文介绍了磁耦合无线电能传输的概念、 原理模型.对磁耦合模型使用maxwell进行了建模以及联合仿真分析， 结合实际工程应用需求， 设计者可以更加形象地了解磁耦合无线电能传输的应用.未来， 磁耦合无线电能传输的模块化、 小型化和协同化是应用的主流.

参考文献：

[1]Andre K, Aristeidis K, Robert M, et al.Wireless power transfer via strongly coupled magnetic resonances[J]. Science， 2007， 317(5834)： 83-86.

[2]Sample A P， Meyer D A， Smith J R. Analysis， experimental results and range adaptation of magnetically coupled resonators for wireless power transfer[J]. IEEE Transactions on Industrial Electronics， 2011， 58(2)： 544-554.

[3]Yu X， Sandhu S， Beiker S， et al. Wireless energy transfer with the presence of metallic palanes[J]. Applied Physics Letters， 2011， 99(21)： 1-3.

[4]OLEV公司. www.olevtech.com.

[5]Imura T， Hori Y. Maximmizing air gap and efficiency of magnetic resonant couling for wireless power transfer using equialent circuit and neumann formula[J]. IEEE Transactions on Industrial， 2011， 58(10)： 4746-4752.

[6]Koh K， Beh T， Imura T， et al. Impedance matching and power divison using impedance inverter for wireless power transfer via magnetic resonant coupling[J]. IEEE Transation on Industry Applications， 2013， 50(3)： 2061-2070.

[7]Teck Chuan Beh， Kato M， Imura T， et al. Automated impedance matching system for robust wireless power transfer via magnetic resonance coupling[J]. IEEE Transactions on Industria Electronice Coupling， 2013， 60(9)： 3689-3698.

[8]Cannon B L， Hoburg J F， Stancil D D， et al. Magnetic resonant coupling as a potential means for wireless power transfer to multiple small rrceivers[J]. IEEE Transactions on Power Electronices， 2009， 24(7)： 1819-1825.

[9]杨庆新，张献，李阳，等.无线电能传输技术及其应用[M].北京：机械工业出版社，2014.

[10]杨宏正，曹军青，王三胜，等. 线圈磁耦合模型仿真及其应用[J]. 测试技术学报， 2016，30(6)：471-477.

Yang Hongzheng， CAO Junqing， Wang Sansheng, et al. Simulation of magnetic coupling model of coil and its application[J]. Journal of Test and Measurement Technology, 2016，30(6)：471-477. (in Chinese)

[11]Domingo M C. Magnetic induction for underwater wireless communication networks[J]. IEEE Transactions on Antennas & Propagation, 2012, 60(6): 2929-2939.

[12]傅文珍，张波，丘东元, 等. 自谐振线圈耦合式电能无线传输的最大效率分析与设计[J]. 中国电机工程学报，2009(18)： 21-26.

Fu Wenzheng， Zhang Bo， Qiu Dongyuan, et al. Maximum efficiency analysis and deign of self-resonance coupling coils for wireless power transmisson system[J]. Proceedings of the CSEE， 2009(18)： 21-26. (in Chinese)

[13]蒋维，傅文珍，王蕊玲，等. 一种小功率的谐振耦合电能无线传输系统仿真[J]. 嘉兴学院学报， 2012(3)： 107-110.

Jiang Wei， Fu Wenzheng， Wang Ruiling, et al. A low-power system simulation of wireless energy transfer based on resonant coupling[J]. Journal of Jiaxing University， 2012(3)： 107-110. (in Chinese)

[14]柏杨，黄学良，邹玉炜，等. 基于超声波的无线电能传输的研究[J]. 压电与声光， 2011(2)： 324-327.

Bo Yang， Huang Xueliang， Zhou Yuwei, et al. Study of wireless power transfer system based on ultrasonic[J]. Piezoelectrics & Acoustooptics， 2011(2)： 324-327. (in Chinese)

[15]黄学良，谭林林，陈中，等. 无线电能传输技术研究与应用综述[J]. 电工技术学报， 2013(10)： 1-11.

Huang Xueliang， Tan Linlin， Chen Zhong, et al. Review and research progress on wireless power transfer technology[J]. Transactions of China Electrotechnical Society， 2013(10)： 1-11. (in Chinese)