利用分段建模方法建立海南省主要树种立木材积模型

（国家林业局 中南林业调查规划设计院，湖南 长沙 410014）

森林是陆地生态系统的主体，是国民经济和社会发展的物质基础，是维持生态平衡和改善生态环境的重要保障，在应对全球气候变化中发挥着不可替代的作用。森林蓄积是衡量森林资源的主要指标之一，而立木材积模型是森林蓄积量的“度量衡”。在我国林业生产实践中，二元立木材积模型是森林蓄积量估计中最常用的计量依据[1]，考虑实际应用便利，二元材积模型建模单元多以树种自然分布区或者省级行政区域为主，因此提高二元立木材积模型精度、保证模型的通用性变得十分重要。

编制二元立木材积模型的方法很多，模型结构主要以山本材积最为常见，为提高模型预估精度和通用性，国内学者在建模样本组织、模型结构优化、建模方法等方面做了大量的研究。贺东北等[2]提出组织通用性二元立木材积模型建模样本应取不少于5个取样径阶，其中最小和最大径阶必取，每个取样径阶下按高径比大、中、小取30株样本，总样本量不少于150株，以保证模型具有广泛适用性。骆期邦等[3]、岑巨延等[4]改进二元立木材积山本式结构，建立可变参数模型，提高了模型的预估精度。胥辉等[5]、曾伟生等[6]、刘镜婷等[7]采用联立方程组建立树高、材积等联立方程组模型，解决各模型之间相容性问题。张连金等[8]、党永峰等[9]、梁文业等[10]为解决模型在小径阶下可能出现明显系统偏差问题，采用分段建模方法建立二元立木材积与地上生物量相容模型，提高了模型预估精度和通用性。陈振雄等[11]考虑橡胶树分枝、区域和品系的区别，采用混合模型方法建立海南省橡胶树二元立木材积模型，以提高模型的预估精度。

本研究以海南省5种主要树种（桉树、木麻黄、马占相思、橡胶树、加勒比松）为研究对象，采用分段建模方法为各树种建立适用于全省的二元立木材积模型，并与传统常规建模方法进行对比分析，以期探讨解决常规模型在各径阶下可能存在的偏估问题，提高模型的通用性。

1 数据来源

本文数据来源于海南省桉树、木麻黄、马占相思、橡胶树、加勒比松立木材积模型研建实测数据。在样本组织方面，各树种样本采集范围尽可能覆盖海南省各个地区，同时尽可能扩大样本变量（胸径、树高）的覆盖范围，以真实反映变量间相关规律的完整性和真实性。桉树、木麻黄、马占相思样本采集区域集中在临高县、儋洲市、屯昌县、琼中县、五指山市、白沙县、琼海市；橡胶树样本采集区域集中在白沙县、保亭县、澄迈县、儋州市、琼海市、琼中县；加勒比松样本采集区域集中在白沙县、屯昌县、澄迈县、五指山市、琼中县。

根据二元立木材积表编制技术规程的要求[12]，本文中桉树、木麻黄、马占相思的取样径阶7个，分别为 6、10、14、18、22、26、28 cm 以上；加勒比松和橡胶树取样径阶6个，分别为6、10、16、22、28、32 cm以上。每取样径阶内要求尽量按树高的实际变化范围分低、中、高（以高径比控制）选取样木，伐倒后分0/10、0.5/10、1/10、2/10、3/10、4/10、5/10、6/10、7/10、8/10、9/10树高处实测直径，采用分段求积的方法获取样木材积数据。根据最新研究结果应利用全部样本来建立模型，充分利用样本信息，使模型的预估误差最小[13]。本次模型研建不分建模样本和检验样本。具体各树种样本实测数据的基本情况见表1。

表1 海南省主要树种立木材积的实测数据Table 1 The general situations of the main tree species of tree volume data in Hainan province

2 方 法

2.1 山本材积式

式（1）中：V为材积（m3）；D为胸径（cm）；H为树高（m）；a、b、c为模型参数。

2.2 分段模型

利用全部径阶的实测数据直接建立二元立木材积模型可能在各径阶中存在一定的偏差，为保证二元立木材积模型的通用性，采用分段建模的方法来消除偏差[3，8-9]。利用分段建模方法需要解决两个核心问题：一是寻找合适的节点；二是保证节点处无缝对接[8]。对第一个问题，本研究根据建模数据散点图以及对常规的二元立木材积模型进行综合分析，同时兼具科学性和实用性，桉树、木麻黄选择胸径10 cm作为分段建模的节点，马占相思、加勒比松、橡胶树选择胸径12 cm作为分段建模的节点。对于第二个问题，本研究通过对模型参数设置限制条件来解决。具体分段模型结构如下：

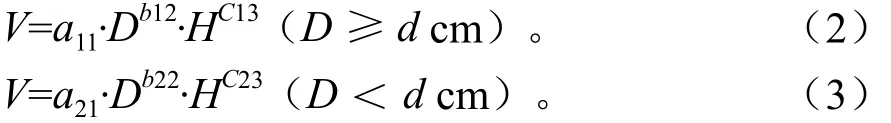
为保证在节点处无缝对接，上述模型参数之间应该满足以下条件：

式中：d为各树种分段模型的节点(10 cm、12 cm)，在模型拟合过程中，先利用D≥dcm的建模数据估计模型（2）中的参数，再通过式（4）的限制条件和利用D＜dcm的建模数据估计模型（3）的参数。

2.3 异方差处理

由于材积数据普遍存在异方差现象，在利用非线性回归方法进行拟合时还需采取措施消除异方差的影响[15]。常用的方法有采用对数回归或者加权回归，本文中均采用非线性加权回归的方法。关于权函数，本文中采用独立拟合方程的方差建立之。

2.4 模型评价指标

为保证所建模型稳定、可靠，本文中采用6个指标来对模型进行评价和检验[12,16]，分别为确定系数（R2）、估计值的标准差（SEE）、总相对误差（TRE）、平均系统误差（MSE）、平均预估误差（MPE）和平均百分标准误差（MPSE），其计算公式如下：

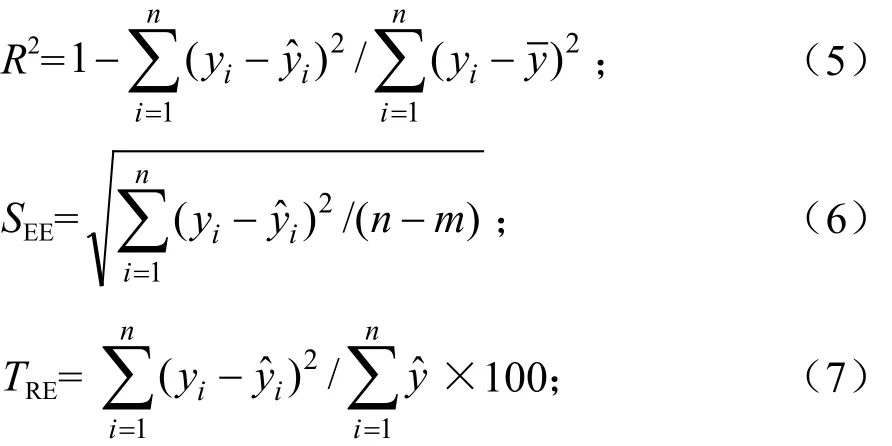
式中：yi为实测观测值；为模型预估值；为样本平均值；n为样本单元数；m为参数个数；tα为置信水平α时的值。R2和估计值的标准差是回归模型的最常用指标，反映了模型的拟合优度；总相对误差和平均系统误差是反映拟合效果的重要指标，二者都应该控制在一定范围内，或者趋于0时效果最好；平均预估误差是反映平均材积估计值的精度指标，值越小预估精度越高；平均百分标准误差是反映平均单株林木材积估计值的精度指标。根据二元立木材积表编制技术规程中对模型行为分析的要求，以及保证各树种二元立木材积模型在各径阶下无明显系统偏差，本研究重点通过利用总相对误差和平均系统误差两个指标分径阶检验模型的通用性。

3 结果与分析

利用海南省5个树种（桉树、木麻黄、马占相思、橡胶树、加勒比松）的立木材积实测数据，分别采用常规模型和分段模型，使用ForStat2.2软件进行参数估计，建立各树种的二元立木材积模型，并对各模型进行评价和检验，各模型参数估计值和评价指标见表2。

由上式可知，P值越大，表明老年人口数量越多，人口老龄化程度越高。因此P可作为衡量人口老龄化程度的变量。将P作为人口老龄化程度的代理变量引入到公式（3）中，得到L(t)与P之间的关系如下：

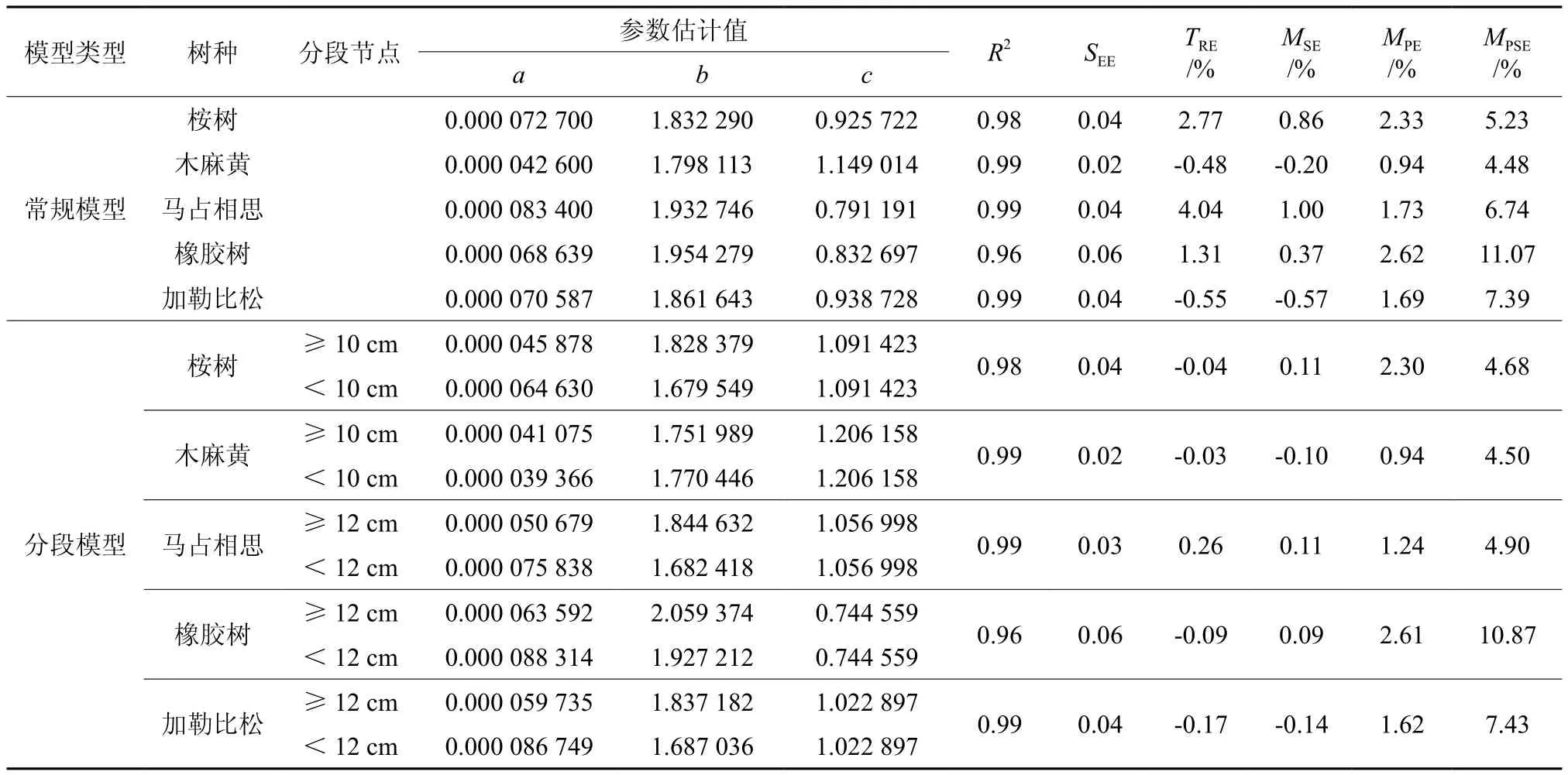
表2 常规模型和分段模型拟合参数及评价指标Table 2 Fitting results and evaluation indexes of conventional models and segmented models

从表2可知，无论常规模型和分段模型，各树种二元立木材积模型拟合效果均很好，预估精度很高，均超过97%，确定系数均达到0.98及以上，总相对误差和平均系统误差均在±3%以内，整体上不存在明显系统偏差。各树种二元立木材积常规模型和分段模型的R2、估计值的标准差、平均预估误差、平均百分标准误差4个评价指标差异较小。对于总相对误差和平均系统误差2个指标，除木麻黄树种以外，其它4个树种分段模型明显优于常规模型。

为保证各树种所建二元立木材积模型的通用性，采用总相对误差和平均系统误差2个指标对各径阶进行检验。从表3、表4可知，木麻黄二元立木材积常规模型和分段模型差异很小，而其它4个树种分段模型通用性要优于常规模型，在各径阶下，分段模型总相对误差和平均系统误差2个指标均能基本保证在±3%以内，常规模型总相对误差和平均系统误差2个指标基本保证在±6%以内。

表3 桉树、木麻黄、马占相思立木材积模型分径阶检验结果Table 3 Testing results of volume models of Eucalyptus, Casuarina equisetifolia, Acacia mangium for different diameter classes

表4 橡胶树、加勒比松立木材积模型分径阶检验结果Table 4 Testing results of volume models of rubber,Caribbean pine for different diameter classes

4 结 论

以海南省桉树、木麻黄、马占相思、橡胶树、加勒比松为研究对象，利用分段建模的方法研建各树种二元立木材积模型，并与常规模型进行对比分析，可以得出以下结论：

（1）从模型的整体评价结果来看，常规模型和分段模型的拟合效果均很好，均符合二元立木材积表编制技术规程的要求，分段模型整体总相对误差和平均系统误差2个指标要优于常规模型。

（2）对常规模型和分段模型各径阶进行检验分析，分段模型能基本保证各径阶下总相对误差和平均系统误差在±3%以内，而常规模型各径阶下总相对误差和平均系统误差在±6%以内。因此分段模型能够有效地改进各径阶下偏估问题，提高模型的通用性。

二元立木材积模型是我国林业行业应用最为广泛的基础计量工具之一，它广泛应用于单株木材积计量，或某一区域内林分材积计量等，因此对模型的通用性提出了更高的要求。根据我国二元立木材积表编制技术规程的要求，二元立木材积模型的适用条件应满足采用独立检验样本进行检验时总相对误差在±3%以内，而未对各个径阶内的总相对误差提出具体的要求。本研究对海南省5种树种建立适用于全省范围的通用型二元立木材积模型，除木麻黄二元立木材积常规模型在各个径阶下总相对误差均在±3%以内，与分段模型差异小以外，其它4个树种各径阶下分段模型总相对误差和平均系统误差指标明显优于常规模型，并且分段模型能基本保证各径阶下总相对误差在±3%以内。因此利用分段模型建立的材积模型的通用性要优于常规模型，该方法可以推广应用到林业数表领域。

参考文献：

[1] 骆期邦,曾伟生,贺东北. 林业数表模型—理论、方法与实践[M]. 湖南: 湖南科学技术出版社,2001:3-34.

[2] 贺东北, 曾伟生, 骆期邦. 通用性二元立木材积模型的建模样本研究[J]. 中南林业调查规划, 2001,20(1):1-9.

[3] 骆期邦,宁 辉,贺东北,等. 二元立木材积动态模型研究[J].林业科学研究, 1992，5(3): 263-270.

[4] 岑巨延. 广西桉树人工林二元立木材积动态模型研究[J]. 华南农业大学学报, 2007,28(1):91-95.

[5] 胥 辉, 吴明山, 叶江霞. 二元立木材积模型的联立方程组估计方法[J]. 林业科学研究, 2009,22(6):788-791.

[6] 曾伟生. 杉木相容性立木材积表系列模型研建[J]. 林业科学研究, 2014, 27(1):6-10.

[7] 刘镜婷,姜立春.大兴安岭不同区域落叶松相容性材积方程及异方差研究[J].林业科学研究, 2016, 29(3): 317-323.

[8] 张连金, 曾伟生, 唐守正. 用带截距的非线性方程和分段建模方法对立木生物量估计的比较[J]. 林业科学研究, 2011,24(4): 453-457.

[9] 党永峰, 王雪军, 曾伟生. 用分段建模方法建立东北落叶松立木材积和生物量方程[J]. 林业科学研究, 2012,25(5):558-563.

[10] 梁文业, 贺 鹏, 肖前辉. 利用度量误差模型和分段建模方法建立云南云杉相容性立木材积和地上生物量模型[J]. 中南林业调查规划, 2014,33(1):8-12.

[11] 陈振雄, 贺东北, 贺 鹏. 利用混合模型方法建立海南省橡胶树立木材积方程[J].中南林业科技大学学报,2016,36(12): 31-36.

[12] 国家林业局. LY/T 2012一2013二元立木材积表编制技术规程[S].北京:中国标准出版社, 2013.

[13] 曾伟生, 唐守正. 立木生物量方程的优度评价和精度分析[J].林业科学, 2011, 47(11 ): 106-113.

[14] 孟宪宇. 测树学[M]. 北京: 中国林业出版社,2006:131-134.

[15] 曾伟生, 骆期邦, 贺东北. 论加权回归与建模[J]. 林业科学,1999, 35(5): 5-11.

[16] 曾伟生, 唐守正. 立木生物量模型的优度评价和精度分析[J].林业科学, 2011, 47(11): 106-113.