诱导改造对大兴安岭蒙古栎低质林土壤养分的时空影响
(东北林业大学 森林持续经营与环境微生物工程黑龙江省重点实验室,黑龙江 哈尔滨 150040)
土壤能涵养水源、保持水土,为森林中生物生长和繁衍提供物质基础和能量保证[1-3]。土壤质量的好坏与森林内林木的正常生长密切相关,两者互相作用,互相影响:土壤养分质量直接影响着林木生长的速度和持续性,而林木生长情况又反作用于土壤养分质量[4-5]。
近年来,大兴安岭林区由于自然和人为因素的双重影响,出现大面积的林木质量低下、水土流失严重的低质残次林[6-7],其主要特点是所在森林郁闭度低、生态系统稳定性差、抵抗自然灾害的能力较弱,任由其发展,大兴安岭林区应发挥的生态效益和经济效益都将大打折扣[8-9]。因此,对大兴安岭林区林分进行合理的诱导改造是十分迫切的。所以很多专家对大兴安岭林区的低质林改造进行了相关的研究,其中最具有代表性的是:曾翔亮等[10]对大兴安岭蒙古栎低质林进行了带状和林窗改造,并对改造后的土壤养分状况进行分析,结果表明林窗改造的改造效果要优于带状改造,且20 m×20 m的林窗改造方式最有益于土壤养分的积累;毛波等[11]对大兴安岭林区的白桦低质林进行了带状和林窗改造,然后对改造后的土壤肥力进行分析,得出了林窗面积为G4(20 m×20 m)时诱导改造中土壤肥力综合评价最高,带宽为S3(14 m)时带状诱导改造中土壤肥力综合评价值最高的结论。但是二者的研究都是基于诱导改造后单一年份的土壤养分指标进行分析,数据说服力不够强,近年来关于大兴安岭林区低质林诱导改造的相关研究中没有对改造后连续多年的土壤养分数据进行统计分析。
综上所述,本研究以大兴安岭林区蒙古栎低质林为研究对象,经过不同带宽的带状改造和不同林窗面积的林窗改造后,采用模糊综合指数法[12]对改造后7 a内的土壤养分指标进行时空变化分析和综合评价,通过分析土壤养分的时空变化规律,确定最适合于大兴安岭蒙古栎低质林的诱导改造方法,为大兴安岭低质林的林地土壤改良提供可行性建议。
1 试验区概况和样地设置
1.1 试验区概况
试验区位于黑龙江省大兴安岭林区的加格达奇林业局(50°34″9.17″~ 50°34″32.00″N,124°23″47.8″~ 124°24″35.1″E),所属翠峰林场174林班。地势平缓,坡向东南,坡度8°。立地条件较好,土壤为棕森土,较为肥沃,土壤厚度22 cm。年平均气温为-1.2 ℃,冬季寒冷漫长,夏季时间较短,气候分明,属于典型的温带大陆性气候。试验区内林分主要类型为蒙古栎Quercus mongolica低质林,平均树高在11 m左右,郁闭度约为0.5,灌木主要为胡枝子Lespedeza bicolor,盖度15%,地被物主要为苍术Atractylodes lancea,盖度30%。
1.2 样地设置
2009年春季,在试验林区内对蒙古栎低质林进行林窗和带状诱导改造。其中6个林窗改造试验区的面积分别为5 m×5 m(G1)、10 m×10 m (G2)、15 m×15 m(G3)、20 m×20 m(G4)、25 m×25 m(G5)、30 m×30 m(G6),林窗沿横坡方向排列(如图1所示)。带状改造为顺山皆伐改造,原则上每条皆伐带设置在同一海拔高度,皆伐带带长均为300 m,带宽分别为6 m(S1)、10 m(S2)、14 m(S3)、18 m(S4)[13]4种(如图2所示)。在未采伐的林地内设置30 m×30 m的对照样地,分别取5个样本点。对改造区针叶幼树全部保留,对其它非目的阔叶树种进行全部清理并在采伐样地内补植樟子松Pinus sylvestris、西伯利亚红松Pinus sibirica、兴安落叶松Larix gmelinii。

图1 蒙古栎低质林林窗改造样地示意Fig.1 Sketch of forest gap reforms about Quercus mongolica low-quality forest

图2 蒙古栎低质林带状改造样地示意Fig.2 Sketch of forest stripreforms about Quercus mongolica low-quality forest
2010—2016年7、8月份在不同改造模式下实地取样,按照“S”型布点法在改造样地和对照样地内各选择4个面积为1 m2的样方,每个样方内选择5个取样点取土,按照四分法混合取样,在每个实验样点取土壤剖面深度为0~10 cm的土壤样本1 kg,带回实验室。对土壤样本进行风干处理,研磨过筛,然后对反映土壤养分的元素含量进行测定。测定方法如表1所示。实验数据运用Excel进行初步处理和运算,利用SPSS软件进行差异性分析和评价模型的构建,绘图用ORIGIN软件完成。

表1 森林土壤元素含量的测定方法Table 1 Method for determination of elements in forest soil
2 土壤综合评价方法
土壤养分质量的优劣是一个相对模糊的概念,因为土壤肥沃与贫瘠并不存在明显的分界线,因此,本研究尝试利用模糊综合指数法对土壤养分进行综合评价。而各项指标对土壤养分造成的影响是有区别的,因此指标权重分配是不同的[14]。主观赋权法多以专家对不同指标的认知为依据,存在很大程度的主观性、随意性,依赖于专家经验[15]。而客观赋权法是根据实验指标值间寻找内在规律,具有较强的数学依据和客观性,由于缺乏经验指导,往往不能如实反映指标的重要性[16-17]。因此,选用兼顾专家实践指导和试验指标值之间客观信息的主客观综合赋权法将能结合双方优点,规避不足,且已经在众多领域中都得到应用[18-19]。
2.1 模糊综合指数法
(1)确定评价标准
首先,确定土壤养分的评价指标U=(有机质,全氮,全磷,全钾,水解氮,有效磷,速效钾),其次确定土壤养分的等级分级V=(一级,二级,三级,四级,五级,六级),从而确定n个养分指标q个级别的标准特征值矩阵S。S=(sij)n×q,其中sij表示第i项养分指标第j个级别的标准特征值。
(2)确定隶属函数矩阵
在U和V均确定后,各样本土壤养分因子与评价等级之间的模糊关系可用模糊矩阵R表示。R=(rij)n×q(i=1,2,…,n;j=1,2,…,q)。其中,rij表示第i种土壤养分指标对第j个级别的隶属度。其隶属关系实际应用中常采用直线段来模拟,为了便于计算,文中用折线型分段函数模拟S型隶属函数。
对于第一级土壤养分质量分数,即j=1,其隶属函数为:
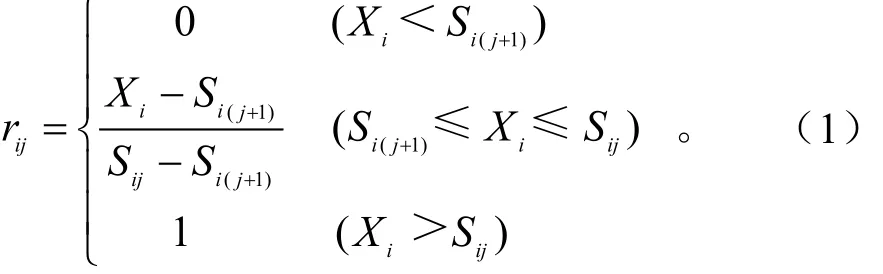
对于第二级到第五级土壤养分质量分数,即j=2~5,其隶属函数为:

对于第六级土壤养分质量分数,即j=6,其隶属函数为:

(3)确定指标权重
本研究选用主客观综合赋权法,采用层次分析法和熵权法结合的方式确定土壤养分指标权重。
(4)计算综合评价结果
已知模糊关系矩阵R和由主客观综合赋权确定的权重W后,对于n种土壤养分因子,可得到其多指标模糊综合评价矩阵B。
对于本文来说,因为土壤养分因子权重接近,运用加权平均型计算比较合适,综合考虑各个指标对土壤养分的影响。

采取将综合评价结果纯量化的形式,转换为综合评价值。

2.2 主客观综合赋权法
(1)层次分析法确定主观权重
设置目标层和系统层:土壤养分G为目标层,设置土壤有机量A1、土壤全量A2、土壤有效量A3为3个系统层。按照递阶层次结构,指标层即为本文中选取的7个反映土壤养分性质的指标:土壤有机质B1、土壤全氮B2、土壤全磷B3、土壤全钾B4、土壤速效氮B5、土壤有效磷B6、土壤速效钾B7。经过综合多名专家的评价结果,得到比较判断矩阵Aij。
根据土壤养分综合评价的相关研究结果,选用方根法计算其单层指标权重:
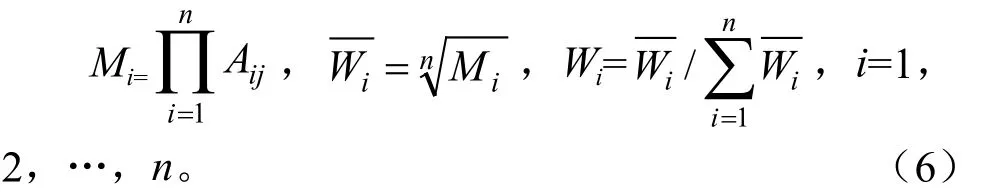
式中:n表示比较判断矩阵的阶数;Wi表示单层次中第i行的指标权重。
然后计算组合权重,计算公式如下:

判断矩阵是否具有一致性[20]:只有矩阵具有一致性,才能利用层次分析法确定指标权重,因此要检验比较判断矩阵的一致性。

根据表2确定比较判断矩阵的平均随机一致性指标(IR)。

表2 平均随机一致性指标IR值Table 2 IR value of average random consistency index
计算出随机一致性比(RC)并进行判断:

如果RC<0.1,则说明比较判断矩阵满足一致性要求,否则认为不满足一致性要求,需要对比较判断矩阵进行调整,直到RC<0.1为止。
(2)熵权法确定客观权重
确定原始矩阵:由m个样地的n个评价指标实测值组成原始矩阵Dm×n。
采用线性比例变换中的正向指标型,即各样地的指标实测值与对应的指标最大值的比值,见式(10),并记标准化后的矩阵为R′。

再通过公式(11)、(12)、(13)计算出土壤养分指标的权重:

式中:pij表示第j个指标下第i个样地的指标值;ej表示第j个指标的熵值;wj表示第j个指标的权重。
(3)确定综合权重
结合主观权向量和客观权向量的结果,采取线性综合赋权确定综合权重,其计算公式为:

式中:W3表示土壤养分指标综合权向量;W1表示土壤养分指标主观权向量;W2表示土壤养分指标客观权向量;μ表示偏好系数,取值范围为0~1。
3 结果与分析
3.1 土壤养分各指标时间变化分析
不同林窗和不同林带的样地各土壤养分指标的时间变化如图3、4所示。
S1、S3、S4、G2样地不同年份土壤中有机质含量有较大的差异,其他的改造样地和对照样地也有差异,但差异性较小。总体而言,各个改造样地在改造后第1年有机质含量较高,后出现下降,在改造后第5、6年土壤中有机质含量又达到最高,改造后第7年又出现小幅度的下降,呈现出波动性。方差分析发现,改造后第7年,G1、G3、G5、G6、S3、S4改造样地中有机质含量与改造后第1年土壤中的有机质含量存在显著差异(P<0.05)。
各改造样地的全氮含量随着时间变化规律不明显。G1、G4样地不同年份土壤中全氮含量有较大的差异,其它的改造样地和对照样地也有差异,但差异性较小。不同的改造样地在时间连续中土壤全氮含量出现不同的变化情况,与年份相关性较小。到改造后第7年,G1、G2、S2、S4改造样地土壤全氮含量与改造后第1年差异显著(P<0.05),改造效果明显。
G1样地改造后第7年土壤中全磷含量最高,与前几年差异显著(P<0.05)。其他改造样地土壤全磷随着时间的推移基本呈先上升后下降再上升的趋势,改造后第1、2年土壤中全磷含量较高,后土壤中全磷含量下降,到改造后第6年、第7年土壤全磷含量又上升。其中,G2、G4、G6改造样地改造后第7年土壤中的全磷含量明显高于改造后第1年土壤中的全磷含量。

图3 带状改造土壤养分各指标随时间的变化Fig.3 Temporal change of soil nutrient indexes in strip reforms

图4 林窗改造土壤养分各指标随时间的变化Fig.4 Temporal change of soil nutrient indexes in gap reforms
改造样地G2、G3、G4土壤中全钾含量随着时间变化呈现先上升后下降的趋势,改造后第2年有小幅度上升,其中有一定的波动,到改造后第6年开始下降;其它改造样地土壤全钾含量随着时间的推移呈现出先上升后下降再上升的趋势,改造后第7年土壤中全钾含量达到最高,且在这些改造样地中与改造后第1年的土壤全钾含量差异性显著(P<0.05)。
S1、S3、S4、G2样地不同年份土壤中速效氮含量有较大的差异,其它的改造样地和对照样地也有差异,但差异性较小。改造样地G1、G3、S3总体上随时间推移呈现先下降后上升的趋势,在改造初期土壤中速效氮含量有所下降,之后呈上升趋势,略有波动,但波动不大,到改造后第7年土壤速效氮含量达到最大。其它改造样地的速效氮含量随时间变化波动较大,但无明显规律性。除改造样地S4、G5、G6外,其它样地改造后第7年土壤速效氮含量与改造后第1年差异显著(P<0.05)。
G2、G4、G5、S1改造样地不同年份土壤中有效磷含量有较大的差异,其它的改造样地和对照样地也有差异,但差异性较小。改造样地随时间变化规律不明显,其中G3、G4、G5、G6、S1、S2、S4样地在改造后第1年土壤中有效磷含量最低,之后呈波动型的增长。改造后第7年全部改造样地土壤的有效磷含量与改造后第1年差异性显著(P<0.05)。
G4、S1、S2、S3改造样地不同年份土壤中速效钾含量有较大的差异,其它的改造样地和对照样地也有差异,但差异性较小。随着时间的变化,其含量出现波动,但未表现出明显的规律。经分差分析发现改造后第7年,G4、G5、S1、S2、S3样地土壤中速效钾含量与改造后第1年土壤中的速效钾含量存在显著差异(P<0.05)。
不同养分指标随时间变化的规律无明显的相似性,单个指标的变化情况对于评价土壤养分无关键的作用,整体无规律可言,所以从单个指标的时间变化看总体土壤养分的质量变化是不可行的。
3.2 土壤养分各指标空间变化分析
改造后7 a内各土壤养分指标的空间变化如图5、6所示。

图5 带状改造土壤养分各指标的空间变化Fig.5 Spatial change of soil nutrient indexes in strip reforms
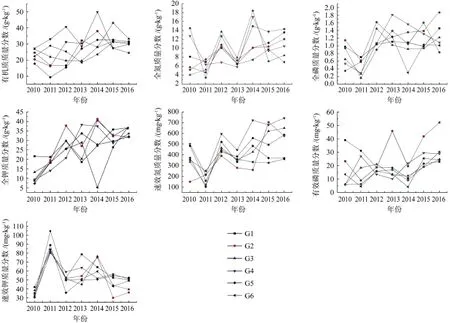
图6 林窗改造土壤养分各指标的空间变化Fig.6 Spatial change of soil nutrient indexes in gap reforms
有机质:改造后第1、2年,对照样地有机质含量与多数改造样地之间差异性不显著,与S4样地差异性显著(P<0.05)。改造后第3年,林窗改造样地有机质含量普遍优于带状改造,对照样地与G2、G4、G6样地差异性显著,与其它样地差异性不明显。改造后第4、5年,G6样地与对照样地差异性显著,有机质含量较高。改造后第6年和改造后第7年,S3样地与其它样地差异性显著,对照样地与S2、S3差异性显著,S3有机质含量最高。
全氮:改造后第1、2年,对照样地全氮含量最高,与多数改造样地差异性显著(P<0.05),改造样地中S3样地全氮含量较高。改造后第3、4年,各样地间差异性不显著(P>0.05)。改造后第5年,对照样地与G3、S4样地差异性显著,与其它样地差异性不显著。改造后第6年,各样地间差异性不显著,G5样地全氮含量最高。改造后第7年,对照样地与G1、S3、G5样地差异性显著,林窗改造样地G5全氮含量最高,与除S3之外的带状改造样地相比差异性显著。
全磷:改造后第1、3年,对照样地与多数改造样地的全磷含量具有显著性差异(P<0.05),G2样地全磷含量较高,G5样地全磷含量较低。改造后第2、4年,对照样地与所有改造样地全磷含量差异性显著,对照样地全磷含量最高,明显高于改造样地。改造后第5、6年,对照样地与多数改造样地差异性不显著(P>0.05)。改造后第7年,对照样地全磷含量明显高于G4、G5、G6改造样地,G2样地全磷含量明显高于对照样地。
全钾:改造后第1年对照样地全钾含量与S1、S2、S4、G3改造样地无显著差异,与其它改造样地相比差异显著(P<0.05)。改造后第2、3年,对照样地除与G2、G4样地差异显著外,与其它改造样地差异性不显著(P>0.05)。改造后第4、5年,对照样地与部分改造样地全钾含量存在显著性差异,且各改造样地间也存在较大的差异。改造后第6年和第7年,对照样地与全部改造样地全钾含量差异性不显著,改造后第7年G2、G6样地全钾含量较高。
速效氮:改造后第1年,对照样地除与S4、G2样地差异性显著(P<0.05)外,与其它改造样地差异性不明显。改造后第2年,对照样地与G2、G4、G6样地差异性不显著(P>0.05),与其他样地有明显的差异。改造后第3年,对照样地速效氮含量低于改造样地,G4、G5样地速效氮含量较高,且与其它样地差异性显著。改造后第4、5年,G2样地速效氮含量较低,且与多数改造样地差异性显著,对照样地与多数改造样地差异性显著。改造后第6、7年,G5、G6样地速效氮含量较低,S2样地土壤中速效氮含量较高。
有效磷:改造后第1、2年,对照样地与个别改造样地(S2、S3、G3)含量差异性较大,且各改造样地中有效磷含量存在较大差距。改造后第3年,对照样地与G1、G2、G5、G6样地有效磷含量差异不明显。改造后第4年,对照样地与多数改造样地中有效磷含量差异显著(P<0.05)。改造后第5年,各样地间差异不大,对照样地与部分改造样地间存在显著性差异。改造后第6年,对照样地有效磷含量与多数改造样地间存在差异,G2样地有效磷含量最高,且与其它改造样地差异性显著。改造后第7年,对照样地的有效磷含量最低,且G2、G4、G5土壤有效磷含量要明显高于对照样地。
速效钾:改造后第1年,对照样地速效钾含量较高,S2、S3样地速效钾含量高于对照样地,但差异性不显著(P>0.05),对照样地与其它改造样地有显著差异(P<0.05)。改造后第2年,对照样地与除S4样地以外的改造样地土壤有效钾含量差异性显著,G6、S1样地含量较高。改造后第3—第5年,部分改造样地速效钾含量高于对照样地,部分改造样地速效钾含量低于对照样地,且存在明显的差距,但具体样地每年都有不同。改造后第6年、7年,G4、G6样地中土壤速效钾含量较高,其中改造后第6年G2样地速效钾含量明显低于对照样地,改造后第7年S1样地速效钾含量较低,但与对照样地差异性不显著。
不同养分指标空间变化的规律也无明显的相似性,单个指标的变化情况对于评价土壤养分无关键的作用,整体无规律可言,所以从单个指标的空间变化看总体土壤养分的质量变化是不可行的。因此,综合评价土壤养分的时空变化对实际改造效果的土壤肥力评价才是有意义的。
3.3 土壤养分时空变化综合评价
3.3.1 土壤各项养分的权重
(1)层次分析法
经过专家讨论和一致性检验,得到土壤各项养分的比较判断矩阵,结果如表3~表6所示。

表3 G-A比较判断矩阵Table 3 Comparison judgment matrix of G-A

表4 A1-B比较判断矩阵Table 4 Comparison judgment matrix of A1-B

表5 A2-B比较判断矩阵Table 5 Comparison judgment matrix of A2-B

表6 A3-B比较判断矩阵Table 6 Comparison judgment matrix of A3-B
根据公式(6),求出各单层次的指标权重;根据公式(7)计算组合权重,得到土壤各指标的权重,即土壤养分主观权向量W1=(0.1768,0.1310,0.1158,0.1068,0.1732,0.1525,0.1439)。
(2)熵权法
土壤养分指标的熵值越小,说明其在综合评价时的作用越大,应该赋以较高的权重[21]。
通过公式(11)、(12)、(13)计算出土壤养分指标的权重。运用MATLAB软件计算出土壤养分权重W2,即土壤养分客观权向量W2=(0.1465,0.1454,0.1528,0.1170,0.1312,0.1549,0.1522)。
(3)综合赋权
根据公式(14)计算综合权重,本研究中μ取0.5,从而得到土壤养分评价指标的综合权重W3=(0.162,0.138,0.134,0.112,0.152,0.154,0.148)。将综合赋权所得的权重值作为最终土壤养分各项指标的权重。
3.3.2 土壤养分模糊综合评价
(1)确定评价标准
本研究的土壤养分评价标准选用全国第二次土壤普查养分分级标准[22],可以得到标准特征值矩阵S。

(2)确定隶属函数矩阵
根据公式(1)、(2)、(3),可求出各诱导改造样地和对照样地的隶属关系矩阵,以改造后第7年为例进行计算。


(3)确定指标权重
综合权重W=(0.162,0.138,0.134,0.112,0.152,0.154,0.148)。
(4)计算综合评价值
利用上述求得的隶属关系矩阵R以及各指标的综合权重W,根据公式(4)、(5)计算出不同改造模式的综合评价结果。综合评价值越低,说明土壤养分等级越高,土壤养分质量越好。2010—2016年7 a内11块样地(包括1块对照样地,10块改造样地)的综合评价值如表7所示。

表7 各样地连续7年综合评价值Table 7 Comprehensive evaluation values for the past seven years
总体而言,对照样地和各改造样地在改造后第1年和第2年土壤养分综合评价值较高,土壤养分等级处在第三等级左右,土壤养分质量较差。改造后第5年至第7年,各改造样地土壤养分综合评价值空间变化规律明显,S2、S3、G4改造效果优势明显,且各样地土壤养分等级均处在2以下,土壤肥沃,说明诱导改造在5 a后对土壤养分有明显的改善作用。
在带状改造中,S2、S3在7 a内变化趋势基本一致,总体呈先下降后上升的趋势,且趋势较平缓,在改造后第5年综合评价值达到最小值,分别为1.668、1.565。S1、S4变化趋势较为一致,在改造后第4年综合评价值最小,分别为1.697、1.676。带状改造中前3 a包括对照样地在内的5个实验区土壤养分综合评价值较为接近,从改造后第4年起,改造后的样地土壤养分出现优于对照样地的趋势。改造后第5年最小值出现在S3样地,为1.565;改造后第6年和第7年最小值均出现在S2样地,为1.693。S2样地的改造方式是最适宜的带状改造模式。
在林窗改造中,G2和G4在7 a内变化趋势基本一致,趋势较为平缓,在改造后第5年达到最小值,分别为1.563、1.579。G1、G3、G5、G6土壤养分综合评价值变化趋势基本一致,在改造后的一两年内,土壤养分质量下降,改造3 a后土壤养分综合评价值开始减小,G3与G5在改造后第6年达到最小值,G1与G6在改造后第5年达到最小值,在第6、7年略有增大。在林窗改造中G4效果较好,改造后第6、7年,所有林窗改造综合评价值均低于对照样地。
4 结论与讨论
土壤养分是土壤肥力综合评价的核心所在,是土壤肥力的根本[23]。林分经改造后,森林中的气候发生较大的变化,光照、温度、湿度改变,微生物活动加剧,使土壤养分情况受到影响[24]。本文中以大兴安岭蒙古栎低质林诱导改造后连续7 a的土壤养分观测数据为切入点,研究不同诱导改造方式对土壤养分的影响,寻找最适合大兴安岭蒙古栎林的经营方式。
选取科学的方法对土壤养分各指标权重进行合理分配,有利于提升土壤养分质量分数等级评价的准确性和精度。本研究在赋权时采用主客观综合赋权,既能发挥专家的经验优势,又能够利用客观实验数据,使得指标权重更具有科学性。权重结果从高到低排列为有机质(0.162)>有效磷(0.154)>速效氮(0.152)>速效钾(0.148)>全氮(0.138)>全磷(0.134)>全钾(0.112),说明有机质和有效磷是大兴安岭蒙古栎林土壤养分重要的影响因子。
同一改造样地土壤养分各项指标随时间变化规律不明显,且同一年内不同改造样地的土壤养分各项指标的变化也无明显规律,很难直观对土壤养分质量优劣进行判断。文中采用模糊综合指数法建立综合评价模型,得到各诱导改造方式的土壤养分综合评价值,以此对诱导改造效果进行分析。结果表明在带状改造中各改造样地综合评价值年间变化较为一致,改造后第4年、第5年土壤综合评价值达到最小值,后有小幅度的增大,但趋势平缓。林窗改造中各样地综合评价值时间趋势较为一致,改造后第5年、第6年达到最小值,土壤养分情况较好,随后年份中评价值有所上升。改造初期采伐改变了森林中的气候条件,土壤养分质量较差,随着时间的变化,大量的枯枝落叶得以保留,土壤中微生物活跃,这在一定程度上提高了土壤养分质量,一段时间后土壤养分变化趋势变缓,甚至出现下降趋势。在7 a内,森林生态系统得以重新构建并趋于稳定,土壤养分质量良好。改造后的第7年,经诱导改造后的样地土壤养分综合评价值均低于对照养地。在带状改造中,10 m带宽的改造方式优势明显,林窗改造中20 m×20 m林窗改造效果最好。这主要是因为随着改造带宽和林窗面积的增加,林地内的光照温湿度等微气候环境发生改变,林地内枯落物加快分解,土壤养分明显升高,促进地上植被生长,而当改造带宽和林窗面积过大时,林分郁闭度低,改造后林木的生长量远不及改造时失去的生物量,林冠对降雨的截留作用弱,容易引起地表径流,土壤易受侵蚀,造成水土流失,导致土壤养分降低。
大兴安岭蒙古栎低质林在诱导改造7 a后各样地土壤养分质量分数等级均在2级左右,说明经诱导改造后各样地土壤非常肥沃,这与大兴安岭林区实际情况是比较吻合的。但值得注意的是,由于植物生长周期较长等客观因素的影响,森林生态系统的循环更新也将是一个漫长的过程,本研究的研究年限仅局限在7 a内,此外林地土壤状态除受到土壤养分影响外,还与土壤的含水率、容重、微生物活动等有关,因此这就需要对土壤养分进行长期观测,同时要对土壤的其它特性进行监测,这将是今后研究的侧重点,为更好地改良林地内土壤提供科学指导。
参考文献:
[1] 杨晓娟, 王海燕, 刘 玲,等. 东北过伐林区不同林分类型土壤肥力质量评价研究[J]. 生态环境学报, 2012(9):1553-1560.
[2] 孟 楚, 王 琦, 郑小贤. 北京八达岭林场水源涵养林结构与功能耦合机理研究[J]. 中南林业科技大学学报, 2017, 37(3):69-72.
[3] 李 湃, 李应珍, 杨雪峰,等. 大兴安岭林区低效林补植改造生态效应分析[J]. 森林工程, 2016, 32(3):36-39.
[4] 云 雷, 毕华兴, 马雯静,等. 晋西黄土区林草复合系统土壤养分分布特征及边界效应[J]. 北京林业大学学报, 2011,33(2):37-42.
[5] 陈百灵, 董希斌, 毛 波,等. 低质林改造后土壤养分变化综合评价[J]. 中南林业科技大学学报, 2015,35(9):65-70.
[6] 李 勇, 刘继明, 董希斌,等. 大兴安岭林区低质林成因及改造方式[J]. 东北林业大学学报, 2012, 40(8):105-107.
[7] 孙 楠, 郭树平. 带状皆伐后更新密度对植物多样性的影响[J]. 森林工程, 2016, 32(6):15-19.
[8] Mckechnie J, Maclean H L. Implications of emissions timing on the cost-effectiveness of greenhouse gas mitigation strategies:application to forest bioenergy systems[J]. Global Change Biology Bioenergy, 2014, 6(6):414-424.
[9] 黄继红, 郭仲军, 刘永红,等. 陕西省宁陕县天然林保护工程生态效益价值评估[J]. 西北林学院学报, 2016, 31(1):298-303.
[10] 曾翔亮, 董希斌, 高 明. 不同诱导改造后大兴安岭蒙古栎低质林土壤养分的灰色关联评价[J]. 东北林业大学学报,2013,41(7):48-52.
[11] 毛 波, 董希斌, 宋启亮,等. 大兴安岭白桦低质林改造后土壤肥力的综合评价[J]. 东北林业大学学报, 2014,42(10):72-76.
[12] Margaret G Schmidt, Hans E Schreier, Pravakar B Shah. A GIS evaluation of land use dynamics and forest soil fertility in a watershed in Nepal[J]. International Journal of Geographical Information Science, 1995, 9(3):317-327.
[13] 张 泱, 宋启亮, 董希斌. 带状皆伐改造对小兴安岭低质林土壤养分的影响[J]. 东北林业大学学报, 2013,41(6):33-37.
[14] Bailador G, Trivi, Graci O. Pattern recognition using temporal fuzzy automata[J]. Fuzzy Sets & Systems, 2010, 161(1):37-55.
[15] 谭三清, 王湘衡, 肖 维,等. 基于复杂网络的森林健康评价研究[J]. 中南林业科技大学学报, 2015,35(8):13-16.
[16] 梁 杰, 侯志伟. AHP法专家调查法与神经网络相结合的综合定权方法[J]. 系统工程理论与实践, 2001, 21(3):59-63.
[17] 张 甜, 朱玉杰, 董希斌. 小兴安岭用材林土壤肥力综合评价及评价方法比较[J]. 东北林业大学学报, 2016,44(12):10-14.
[18] 于 勇, 周大迈, 王 红,等. 土地资源评价方法及评价因素权重的确定探析[J]. 中国生态农业学报, 2006, 14(2):213-215.
[19] 袁 菲, 张星耀, 梁 军. 基于干扰的汪清林区森林生态系统健康评价[J]. 生态学报, 2013, 33(12):3722-3731.
[20] Subramanian N, Ramanathan R. A review of applications of Analytic Hierarchy Process in operations management[J].International Journal of Production Economics, 2012, 138(2):215-241.
[21] 彭铁光, 熊 曦. 熵权综合评价法在林业投入与生态环境协调度评价中的应用[J]. 中南林业科技大学学报, 2016,36(4):135-140.
[22] 曾翔亮, 董希斌, 宋启亮,等. 阔叶混交低质林诱导改造后土壤养分的模糊综合评价[J]. 东北林业大学学报, 2013, 41(9): 50-53.
[23] 骆伯胜, 钟继洪, 陈俊坚. 土壤肥力数值化综合评价研究[J].土壤, 2004, 36(1):104-106.
[24] 纪 浩, 董希斌. 大兴安岭低质林改造后土壤肥力综合评价[J].林业科学, 2012, 48(11):117-123.

