基于改进斜投影算子的极化域通信抗干扰技术

,,

(解放军理工大学 通信工程学院,南京 210007)

0 概述

在现代电子战的条件下,干扰与抗干扰技术始终是一个互相博弈的过程。传统的抗干扰技术主要有扩频和跳频技术,其本质都是将信号分散到尽可能宽的频谱上,以避免特定形式干扰,但主要代价是使用了较大的频谱资源且宽带的收发信机体积也相对较大。对电磁波在极化域的探索最早在雷达领域展开,由于极化捷变及极化分集[1-3]等在工程实践上取得较大突破,因此近些年极化特性也被用于无线通信系统中。目前在极化分集、极化频谱感知、极化调制、极化复用、极化多址等领域[1]国内外学者已经全面展开研究。雷达实现抗干扰的本质利用在于极化域干扰信号与目标信号的差异[4],受此启发,本文探索在无线通信系统中的极化域抗干扰技术。

在信号的极化域,极化匹配滤波[5-8]能够有一定的干扰抑制的效果,但其性能往往难以满足实际的抗干扰需求。斜投影算子[9]是一种较为成熟的信号分离手段,且对目标信号的损伤最小。随着高速率数字信号处理器的不断发展,以及高极化鉴别度的天线系统的应用,结合虚拟极化技术可快速产生捷变的极化信号。利用斜投影算子[10-13]设计出极化滤波器,对已知极化状态的干扰具有较好的滤除效果,但是其本身也有很多缺点。本文对传统的斜投影极化滤波器的性能进行研究,分析其自身的局限性,利用改进型的滤波器,设计针对不同干扰场景的抗干扰技术以及干扰抑制技术,并对比抗干扰效果。

1 斜投影极化滤波器

1.1 极化的表征及快速变极化信号产生

极化作为电磁波的重要属性,表示电磁波的电场矢量在传播截面上随时间变化的轨迹。任意的完全极化状态可以在Poincare球面表示[1],例如使用Jones矢量表征时,选定任意一组正交的极化(H,V)作为基底,用电场表示交变电磁场即可,其表示为:

(1)

其中,γ表示极化角,指在Poincare球面上该极化状态与水平极化状态之间的夹角,取值范围为[0,π/2];δ指的是极化辅角,指该极化和水平极化构成的圆面与线极化面之间的夹角,范围是[0,2π];E为电磁波幅度;ω为载波频率。

任意极化状态合成技术是将极化应用于无线通信系统中的关键技术之一。文献[14]提出使用天线阵列实现任意状态的极化波,但该种技术实现难度大,所需成本也相对较高。随着高速的数字信号处理器和高极化鉴别度天线的发展,与传统的硬件变极化器件不同,虚拟极化技术以及VPA技术通过数字信号处理方式产生和接收任意极化状态[15]。其利用双通道进行幅度和相位加权后反馈给双正交极化天线(Orthogonal Dual Polarized Antenna,ODPA),即可在空间合成具有任意极化状态的电磁波。该技术具有较高的灵活性以及较低的成本等特点,因此本文采用虚拟极化技术收发极化信号。

1.2 斜投影算子

若S,I以及[S,I]都是列满秩矩阵,则定义子空间〈I〉在子空间〈S〉上的斜投影算子为:

(2)

其中,†表示矩阵的伪逆,H表示矩阵的Hermitian变换。根据斜投影算子性质有PSIS=S和PSII=0。式(2)进一步化简为:

(3)

1.3 传统的斜投影滤波器性能分析

在极化域中,目标信号的极化状态为S,被表示为[cosγS,sinγSexp jδS]T,其已调信号为s(t),简写为α,干扰信号的极化状态为I,表示为[cosγI,sinγIexp jδI]T,其已调信号为i(t),简写为β,则接收信号为:

y(t)=Sα+Iβ+n

(4)

其中,n为二维高斯白噪声,每一维噪声均值为0,功率谱密度为σ2。经过式(3)的斜投影滤波器后,可以实现对干扰信号的滤除。为了获得标量输出,将斜投影滤波器的矢量结果投影到目标空间R=[cosγS,sinγSejφs]T中,所以斜投影滤波器的参数设定为:

(5)

(6)

其中,Δγ是角度估计的误差。信号的估计误差对斜投影滤波器性能的影响如图1所示。

斜投影极化滤波器在滤除干扰的同时也将系统噪声放大,对噪声放大的程度与两极化状态在Poincare球面距离有关,所以引入极化相似度的概念。如图2所示,任意2个极化状态P1和P2,将其相似度定义为:

(7)

其中,|·|表示矢量模值,‖·‖表示矢量范数,定义相似度角ζ的取值范围为[0,π/2],极化度的取值介于0和1之间。ρ(P1,P2)的取值越大,ζ的取值越小,则P1和P2的极化相似度越高,反之亦然。

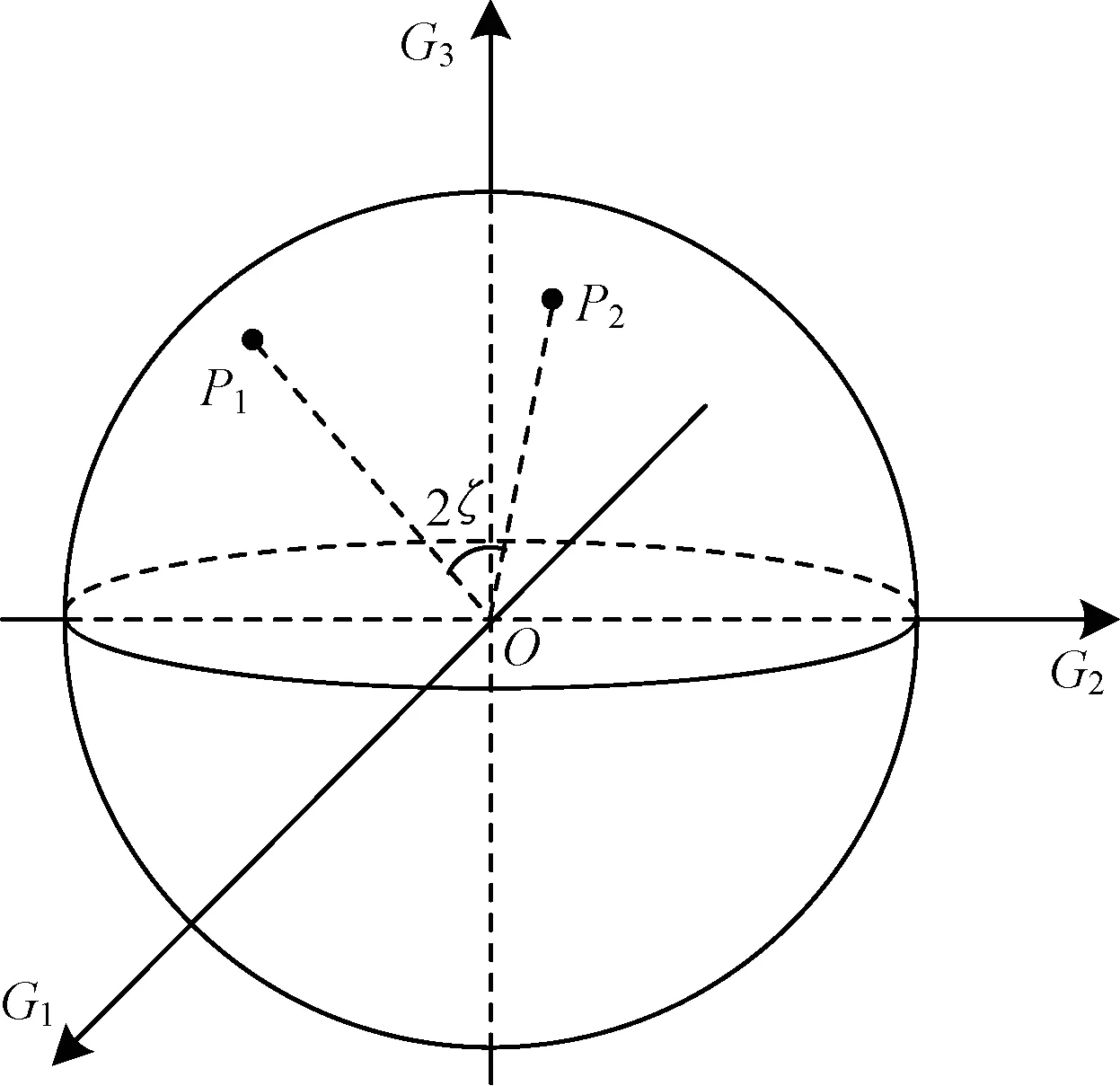
图2 Poincare球上两极化状态极化度

根据文献[11]可知,噪声通过斜投影滤波器后也会被放大,其输出ΔsSNR与ζ的关系为:

(8)

若要尽可能小地放大噪声,则需要根据干扰信号的极化状态选择发射端匹配的极化状态,如图3所示。

图3 ΔsSNR与相似度角ζ之间的关系

1.4 传统斜投影极化滤波器的主要缺点

如图1所示,极化滤波器的性能与极化状态估计精确度有着较大的关系,其性能随着估计误差的增大而不断下降,且目标信号与极化信号之间的极化角差异越大,性能越优。若要满足斜投影算子列满秩条件,则只能消除一种极化状态的干扰形式。在电子对抗中,干扰方将会不惜代价,例如采用多极化干扰或者随机极化干扰,或者灵巧式干扰等,传统的斜投影极化滤波器将无法应用。为了适应多种通信抗干扰的场景,本文提出不同的改进型极化滤波器,以达到更好的抗干扰效果。

2 极化发射信号优化

2.1 干扰极化状态

极化状态估计算法[16-17]虽然估计的精确度在一定程度上存在误差,但若发射的目标信号的极化状态与干扰信号相似度越低,则斜投影滤波器性能越好。

(9)

估计误差Δγ设为1°,根据式(6)、式(8)、式(9),选择不同发射极化状态,SINR得到如图4所示。从图中明显看出与干扰极化相似度越低的目标信号抗干扰能力越强。因此,当探测出干扰信号的极化状态之后,通过优化发射信号的极化状态,实现最大程度的抗干扰效果。

图4 不同发射极化状态时的信干噪比

2.2 转发式极化干扰信号

当干扰方采用转发式干扰时,目标信号与干扰相似度接近1,这时斜投影滤波器性能急剧恶化。所以,借鉴跳频抗干扰的思路,发射信号在极化域设计“跳极化”的方案。即预先在Poincare球面选取相应数目的极化状态,收发双方已知相同的“跳极化图案”。利用直达信号与转发干扰到达接收端的时间差,发射端根据“跳极化图案”改变发射极化状态,接收端也根据“跳极化图案”更新最新的极化滤波器设计参数。

3 斜投影极化滤波器设计

斜投影算子需要满足列满秩条件,因此当干扰极化状态数目不止一个时,[S,I]不满足列满秩条件。目前针对存在M个干扰(I1,I2,…,IM)的情景,利用非线性极化矢量变换(Non-linear Polarization Vector Translation,NPTV)重新构建改进型斜投影算子,直接在极化域消除干扰信号。定义NPTV为:

(10)

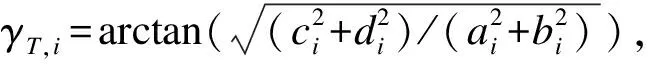
(11)

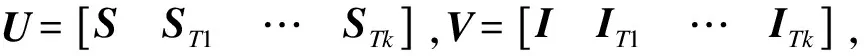
(12)

y=HUVY=HUV[U,V][α,β1,…,βm]=

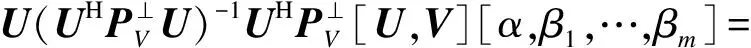
(13)

其中,#代表2k×1的矩阵。从式(13)看出,利用非线性变换的增广矩阵即可构建新的斜投影极化滤波器,能够有效滤除多个极化干扰电磁波,得到目标极化状态。因此,采用非线性极化矢量变换的方式可以有效抑制多种极化状态同时干扰的场景。

4 随机极化波干扰

随机极化波通常指的是在观测期间矢量端点传播空间给定处描绘轨迹难以确切给出,需要对电磁波进行动态的统计观点研究。假设干扰随机极化波为平稳随机信号,则具有一定的二阶统计特性,且与发射信号不相关。传统的斜投影滤波器对于随机极化波完全失效。

若存在随机极化波干扰,接收信号为:

y(t)=Sα+Iβ+n=X+n=Sα+w

(14)

其中,X为信号和干扰,w为随机的干扰以及噪声的组合,则接收信号的y(t)的自相关矩阵为:

Ryy=E[y(t)yH(t)]=E[(X+n)(X+n)H]=

Rxx+σ2E

(15)

假设高斯白噪声的功率为σ2,则噪声与信号之间的自相关矩阵的关系为:

(16)

(17)

(18)

{S[SH(Ryy-σ2E)†S]-1·

SH(Ryy-σ2E)†}TR*

(19)

通过滤波器的参数可知,目标极化状态已知的情况下,只要对噪声的方差准确地估计即可。

为了进一步探究滤波器性能,w自相关矩阵R0=IRββIH+σ2E=RII+σ2E。为了进一步分析极化滤波器在该种干扰下的性能,根据Gauss-Markov理论,目标信号的线性无偏估计为:

(20)

信号估计误差的方差为:

(21)

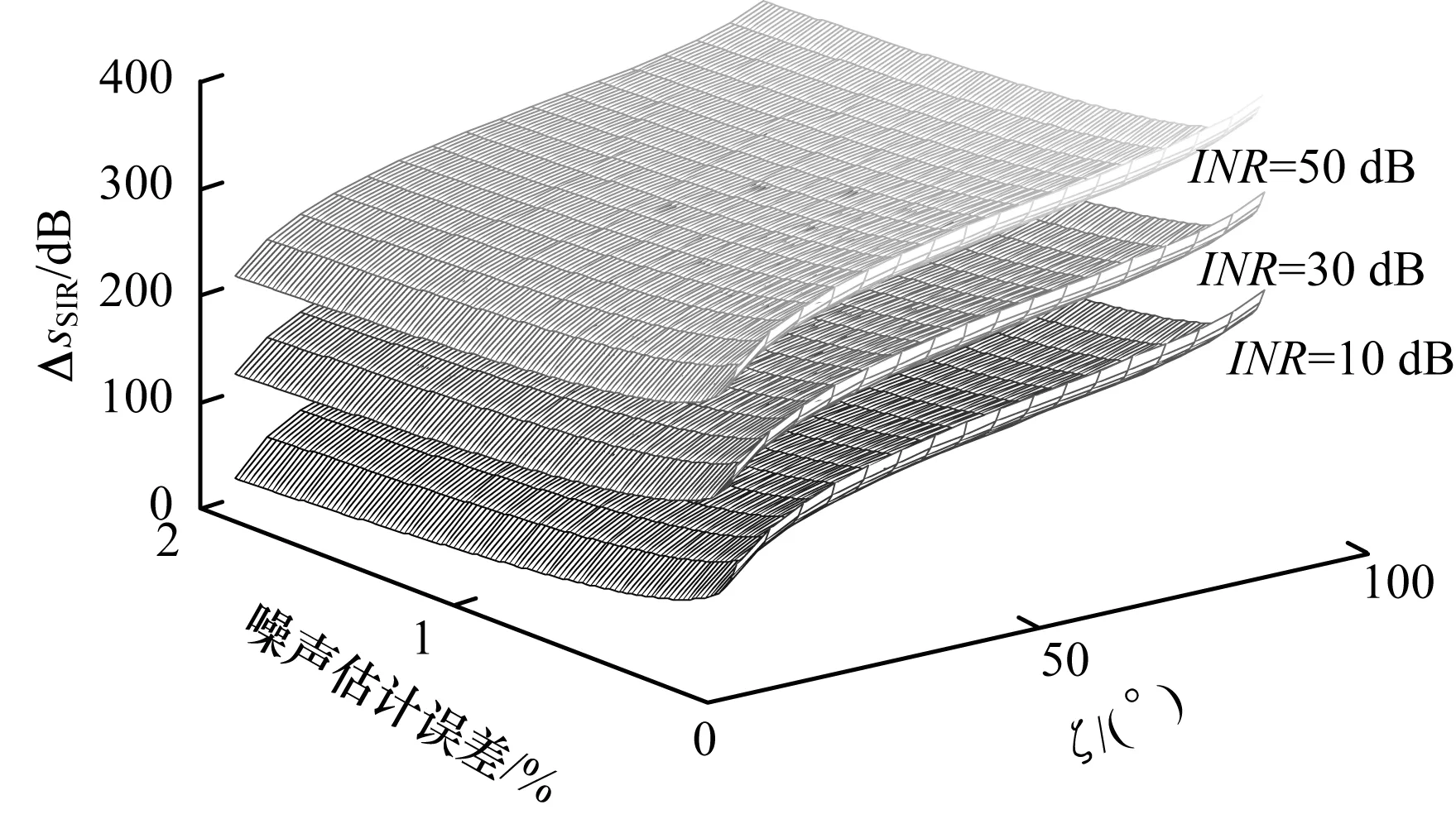
图5 ΔsSIR与噪声估计误差与相似度角ζ的关系

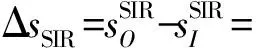
(22)

因此,对于未极化波干扰时,使用斜投影滤波器可以实现一定的干扰抑制作用。图6为斜投影算子滤出随机极化波效果图,其中sSNR=10 dB,RSS=RII。

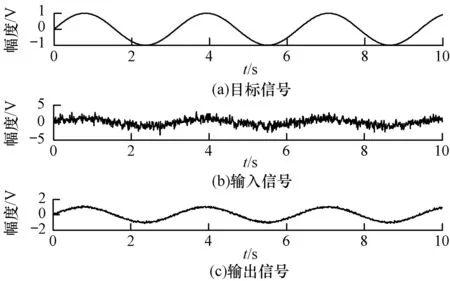
图6 斜投影滤波器滤除随机极化波示意图

5 结束语

本文通过对传统斜投影极化滤波器的主要特点进行分析,设计降低极化相似度等针对不同场景的最优极化域通信抗干扰信号。针对多种极化干扰信号的场景,采用非线性极化矢量变换的增广斜投影算子设计极化滤波器。根据接收信号的统计特性,针对随机极化波干扰设计改进斜投影滤波器。计算及仿真结果表明,该滤波器具有较好的抗干扰性能以及干扰抑制能力。

[1] GUO Caili,LIU Fangfang,CHEN Shuo,et al.Advances on exploiting polarization in wireless communications:channels,technologies,and applications[J].IEEE Com-munications Surveys & Tutorials,2016,19(1):125-166.

[2] ANDREWS M R,MITRA P P,DECARVALHO R.Tripling the capacity of wireless communications using elec-tromagnetic polarization[J].Nature,2001,409(6818):316-318.

[3] LU Ping,MIHAILOV S J.Power penalty of bragg grating based optical add-drop multiplexers in the presence of polarization mode dispersion and polarization dependent loss[J].Indian Journal of Gerontology,2007:114-115.

[4] 施龙飞,任 博,马佳智,等.雷达极化抗干扰技术进展[J].现代雷达,2016,38(4):1-7.

[5] 刘 涛,胡生亮,陈 旗,等.基于极化变换的极化匹配滤波器及其通带理论[J].电波科学学报,2011(3):450-457.

[6] 李艳玮,王雪瑞.极化SAR图像去相关目标检测改进算法[J].计算机工程,2016,42(9):235-239.

[7] 田心记,李 亚,宋 成.双极化天线MIMO中SAST编码性能分析[J].计算机工程,2013,39(12):45-48.

[8] 周万幸.一种新型极化抗干扰技术研究[J].电子学报,2009,37(3):454-458.

[9] CAO Bin,LIU Aijun,MAO Xiaopeng,et al.An oblique projection polarization filter[C]//Proceedings of Inter-national Conference on Wireless Communications,Networking and Mobile Computing.Washington D.C.,USA:IEEE Press,2008:1-4.

[10] CAO Bin,YU Jia,WANG Ye,et al.Enabling polarization filtering in wireless communications:models,algorithms and characteristics[J].IET Communications,2013,7(3):247-254.

[11] 张钦宇,曹 斌,王 健,等.基于斜投影的极化滤波技术[J].中国科学:信息科学,2010,40(1):91-101.

[12] 刘爱军,宋立众,王季刚,等.斜投影三维极化滤波[J].哈尔滨工业大学学报,2012,44(3):75-80.

[13] MAO Xiaopeng,LIU Aijun.Oblique projection polarisation filtering for interference suppression in high-frequency surface wave radar[J].IET Radar Sonar Navigation,2012,6(2):71-80.

[14] XIAO Jinjun,NEHORAI A.Optimal polarized beampattern synthesis using a vector antenna array[J].IEEE Tran-sactions on Signal Processing,2009,57(2):576-587.

[15] DONG Wei,FENG Chunyan,GUO Caili,et al.A power amplifier energy efficient polarization modulation scheme based on the optimal pre-compensation[J].IEEE Com-munications Letters,2013,17(3):513-516.

[16] ROUEFF A,CHANUSSOT J,MARS J I.Estimation of polarization parameters using time-frequency representations and its application to waves separation[J].Signal Processing,2006,86(12):3714-3731.

[17] COON J,SANDELL M,BEACH M,et al.Channel and noise variance estimation and tracking algorithms for unique-word based single-carrier systems[J].IEEE Transactions on Wireless Communications,2006,5(6):1488-1496.