基于SimRank的公共自行车站点聚类算法
朱金山,,,
(1.浙江大学宁波理工学院 图书信息中心,浙江 宁波 315100; 2.宁波工程学院 电子与信息工程学院,浙江 宁波 315211)
0 概述
城市公共自行车概念最早起源于欧洲[1-3]。随着20世纪90年代末期以来信息科学技术的发展,不断涌现的新兴信息技术促进了国内外城市公共自行车系统的发展[4-5]。公共自行车相对其他公共交通方式以其方便、符合健康生活的优点逐渐为众人所欢迎。为积极响应绿色生活的号召,我国城市公共自行车系统近年来也在不断发展改进。城市公共自行车系统在迅猛发展的同时,其面临的问题开始逐渐显现:公共自行车分布不均衡,经常会出现“潮汐问题”,即站点容量小而导致“上下班高峰的无法借车,车无法归还”。现有针对潮汐问题的主流解决方案是对整个城市进行区域划分,然后使用部分调度车辆进行区域间调度,最后对其他调度车辆进行区域内的小范围调度[5]。但是这种方法存在以下问题:如何划分区域,如何确定区域间调度的关键站点。
很多学者从站点聚类[6-8]、动态调度[9-10]、站点布局[11]等角度对公共自行车借还数据进行挖掘。由于研究目标不同,这些文献的聚类结果并不能很好地体现城市内自行车的流动趋势。因为这些聚类都是基于站点的静态特征(如站点容量、借还统计数)进行研究,没有考虑站点间联系。一些学者从网络拓扑关系角度出发分析站点之间的相似度,例如:文献[12]使用加权相关网络模拟自行车间关系,若站间地理位置靠近,则构成链路,根据链路权重得到相似值,提出的聚类算法则利用自行车站点状态下的自行车数量计算相似值;文献[13]将公共自行车系统看作Petri网,以Petri网思想去训练,其缺点是缺乏完整的训练数据集。
文献[14]根据欧式距离划定相似站点,并按一定时间区间的出(或入)度数据进行统计,将出(或入)度大的n个站点构成聚类。这个聚类在一定程度上代表了当时自行车从哪些站点流出。受该文献启发,本文基于站点间联系研究城市公共自行车系统的站点聚类问题,提出一种基于SimRank原理的站点聚类算法SCSR。该算法将具有相似来源(或目的地)的站点聚成一类,从而使每个聚类代表一个或几个自行车流的来源(或目标)区域。
1 基本概念
SimRank[15]是一种用于计算拓扑结构中任意2个节点之间相似值的算法,其主要被用于互联网广告、学术论文等相似值计算领域[16-18]。从结构上看,城市公共自行车系统是一个以站点为节点的网络拓扑。但是,站点之间的相似值更多地取决于站点之间的借还记录,而不是站点的位置、自行车桩位数等固定特征。因此,本文以“目标站点借走的自行车到达哪些站点”问题为研究对象,分析站点之间的相似值,并结合SimRank算法思想对站点进行聚类。为简化和更好地描述算法,下面给出城市公共自行车系统的相关概念。
定义1(公共自行车站点拓扑网络) 公共自行车站点拓扑网络G=(V,E)(本文简称站点网络)。站点α、β表示V的2个站点,三元组(α,β,r)表示站点α、β之间有向连接关系。其中,r表示在指定时间内从站点α到站点β的自行车数目,O(α)表示与站点α存在关联的站点集合,Oi(α)表示O(α)的任一元素。
在SimRank算法中,相似值是2个节点连接边之间相似值的平均值。但是由于站点网络的借还数据不是简单的引用关系,而是带有标量的关联关系,同时站点之间的关系也不像文献引用或互联网广告那样所有与其关联的站点就是同类型的,因此本文取目标站点α的每个关联站点Oi(α)与比较站点β的最相近关联站点Oi(β)之间相似度的平均值作为2个站点的相似度。下面给出站点相似值定义。
定义2(站点相似度) 给定2个站点α、β,基于定义1的站点相似度定义如下:
(1)
式(1)用于计算站点网络中任意2个站点α、β之间相似值,对于一个包含n个站点的站点网络,需要计算一个n×n的矩阵。因此,将式(1)写为如下的迭代公式:
(2)
定义3(p-站点相似) 给定相似值阈值p,根据定义2,给定2个站点α、β之相似值满足s(α,β)>p,s(β,α)>p,则称站点α、β是p-站点相似。
定义4(站点聚类) 给定相似值矩阵M(n×n),如果M矩阵元素站点α、β满足p-站点相似,且不存在一个站点γ同时满足以下2个条件:1)站点α、γ属于p-站点相似;2)s(α,β) 基于上一节站点之间相似值的定义,本文给出基于连接关系的公共自行车站点聚类算法的实现过程。整个算法分成2个阶段:首先,根据定义2和定义3计算站点之间的相似值矩阵M,该功能通过函数computeSimilarMatrix实现;然后,根据相似值矩阵M和用户指定的相似值概率阈值p,并结合定义4,将站点归类为不同的聚类,由函数Cluster实现。算法的伪代码如下: 算法1StationMiningByLinkRelation(G,k,c,p) 输入站点网络G,迭代次数k,抑制因子c,概率p 输出站点聚类集合 1.M=computeSimilarMatrix(G,k,c); //M表示相似值矩阵 2.return Cluster(M,p); 站点相似度矩阵M可以通过式(2)和式(3)迭代计算得到。假设n表示站点个数,k表示迭代次数,R(α,β)是相似值矩阵M的元素,存储每次迭代过程中每对节点(α,β)之间的相似值。每次迭代结束时,将其拷贝到相似值矩阵M。算法2给出了站点相似值矩阵的计算过程。首先按式(9)初始化相似值矩阵M(第1行),由函数Initiaze实现;然后对于每两个站点α、β,循环执行如下迭代过程k次:1)针对站点α的连接站点集合O(α)的每个元素Oi(α),从站点α的连接站点集合O(β)找出与其最相似的站点Oj(β),将这两个站点之间的相似值作为O(α)与O(β)的相似值(第7行~第9行);2)计算α的所有连接站点对应值的平均值作为2个站点之间的相似值(第10行和第11行);3)将中间矩阵M*复制到矩阵M以备下一次迭代,迭代结束。函数返回的是迭代计算得到的相似值矩阵M。 算法2computeSimilarMatrix(G,k,c) 输入G、k、c同算法1 输出相似值矩阵M 1.M*=Initiaze(G); 2.i=0; 3.while(i 4. for α,β∈V(α≠β) 5. for each entry Oi(α)∈O(α) do 6. temp←0; 7. for each entry Oj(β)∈O(β) do 8. if(temp 9. temp=R(Oi(α),Oj(β)); 10. R*(α,β)← R*(α,β)+temp; 11. R*(α,β)← R*(α,β)/|O(α)|; 12. CopyMatrix(M*,M); 13.return M; 典型的聚类算法很多,如K-means、CHEMALOEN、DBSCAN等,由于本文聚类问题具有以下约束:1)聚类个数不定;2)个体特征更多是以个体间联系,而不是空间特征;3)事先已经得到每2个站点间的相似值矩阵。因此本文采用CHEMALOEN算法作为本文聚类算法的原型,并根据具体要求做相应修正。站点聚类思想如下:按照站点之间相似值,判断所有p-站点相似的站点集合,并按大者优先原则将站点分成不同聚类。为方便描述,先说明一些关键数据结构设定:数组c[i]表示站点i属于哪个站点的聚类(c[i]==j表示站点i是属于站点j所在聚类,max[i]表示站点i属于站点j所在聚类的最大相似值)。本文聚类算法实现过程如下: 1)针对每个相似值矩阵M的每一列i,执行如下操作:(1)判断相似值矩阵的当前行i是否存在满足定义3的2个条件的站点,如果不存在,则直接跳转到下一次循环;否则跳转到下一步;(2)如果存在多个站点,则将具有最大相似值的站点j设置为站点i的控制站点;(3)判断矩阵元素mij>max[i](站点i、j的相似值大于先前最大相似值),如果是,则将站点i的控制站点更新为站点j;否则直接跳过本次循环。 2)按数组c[i]合并聚类,如果c[i]==j(j!=0),则判断站点i、j是否属于聚类:(1)如果站点i和j不属于任何聚类,那么站点i和站点j组成一个新聚类,聚类控制站点为站点j;(2)如果站点i(或站点j)属于某个聚类,那么站点j(或站点i)加入站点i(或站点j)的聚类;(3)如果站点i、j都属于不同聚类,则将其合并。 本节将以详细的实验结果分析和参数分析来验证SCSR算法的有效性。由于基于关联关系进行自行车站点聚类的算法鲜有报道,与本文算法并没有直接可比性,因此实验仅分析算法结果的现实意义和算法参数的影响。实验数据是宁波公共自行车借还的5 d数据,抽取其中的(借车站点编号、借车时间、还车站点编号、还车时间)为实验数据,同时结合站点信息数据(站点编号、站点名称、站点经度、站点维度等)。实验开发环境为Win7,Visual C++。 与本文最为相关的研究成果是文献[14]挖掘的自行车运动的时空模式。笔者将其作为对比算法。实验数据为6∶00—10∶00借还车数据,以一个街区距离(250 m)为站点间阈值。图1显示了高出度的站点聚类(85号聚类是具有借车频繁的站点集合)。图2显示了高入度的站点聚类(1号聚类是该时间区间内还车频繁的站点集合)。从2个图中可以发现:1号聚类站点是借出自行车较多的站点集合(85号聚类还的自行车较多)。由于这2个聚类并不表示这些自行车的去向(或来源),因此该算法的聚类结果并没有描述城市自行车流,无法在公共自行车调度和自行车车流的小区域划分等领域使用。 图1 高出度聚类 图2 高入度聚类 图3显示了SCSR算法计算得到的聚类结果(参数p为0.7,实验数据为还车数据集合)。其中“水滴形状”表示不属于任何聚类的站点(异常点),不同聚类用不同颜色的形状表示。相对于文献[14]的聚类算法,SCSR算法的聚类结果具有以下特点:1)聚类站点具有更加一致的趋势特征,SCSR算法将具有相同来源的站点聚成一类(聚类所有成员都拥有相同的来源),每个聚类表示一个或多个自行车流聚类的汇集区域;2)聚类具有更加明显的区域特征,与文献[14]算法中出现的聚类(遍布整个闹市区)不同,SCSR算法挖掘出的聚类很少会包括较大区域。 图3 SCSR算法的聚类结果 从图4可以发现聚类A(圆形站点50#,201#,209#)和聚类B(方形站点160#,478#,260#)分别为区域1中2个聚类。2个聚类具有一定的区域重叠性。但是,无论是从站点所在城市功能区来看(聚类B中的160#站点处在鼓楼步行街北面,应该与50#站点更具有相似特征),还是地图位置来看(160#站点与站点50#站点和209#站点更接近),160#站点的特征更接近聚类A,而不是聚类B。笔者通过分析实际还车数据发现:160#站点的还车数据更接近于同聚类的478#站点和260#站点,原因是因为160#站点位于中山公园旁边,每天早上都有很多从江东江北老区过来的市民进行早锻炼,从而导致该站点数据与聚类B站点相似。 图4 SCSR算法的聚类分析 上述分析显示:聚类A是处在商业区和旅游区相结合区域的站点特征,而聚类B是处在天一鼓楼商业区北面边缘站点特征。这个结果是文献[14]算法无法解析出的运动模式。因此,本文提出的SCSR算法得到的聚类具有更加一致的趋势特征和位置特征,能够更好地应用到公共自行车系统的调度策略和城市区域划分等领域。 本文算法涉及到的参数包括阻尼系数C和相似值概率p2个参数,有关SimRank的阻尼系数C的讨论已经有很多文献进行了研究,这里不再进行讨论,本文将其设定为固定值(0.65)。本节重点来分析相似值概率阈值p的变化对算法结果的影响。图5~图8分别显示了不同相似值概率p值(0.68、0.69、0.70、0.71)的算法运行结果。从中可知,阈值p越大,聚类就越少,这是由于聚类算法中各站点关联数据计算后满足p条件的站点随p变大而减少。如图7中的聚类9和聚类29都逐渐消失。另一方面,聚类规模也在逐渐变小。例如:图中47#聚类(圆圈圈出的站点聚类)随着p值的不断增大而聚类规模逐渐变小,57中47#聚类基本遍及江北区“新马路”以南全部区域,而图6中靠近出口的成员站点(处在连接海曙区和江东区的大桥附近,方框标注)不再属于47#聚类的成员站点。而在图7和图8中,47#聚类只包含3个和2个站点,而这些成员基本都处在江北区“新马路”以南人群最密集区域,尤其是图8中2个站点:生宝路自行车租赁点位于宁波外滩附近,而江北行政中心自行车租赁点地处江北行政中心附近,显然这两处都是宁波江北区的人群密集区域。 图6 阈值p为0.69时聚类47的分布情况 图7 阈值p为0.70时聚类47的分布情况 图8 阈值p为0.71时聚类47的分布情况 本文分析当前关于公共自行车站点聚类的研究成果,并针对其不足提出基于SimRank的站点聚类算法。实验结果表明,本文算法得到的站点聚类结果具有准确的自行车流趋势特征和区域特征,能作为站点区域划分、公共自行车调度策略等研究的基础。下一步将把本文算法应用在基于公共自行车轨迹数据的区域划分和自行车调度策略等方面,同时收集更多的公共自行车实验数据用于研究。 [1] BENCHIMOL M,BENCHIMOL P,CHAPPERT B,et al.Balancing the stations of a self-service bike hire system[J].RAIRO-Operations Research,2011,45(1):37-61. [2] GASPERO L D,RENDL A,URLI T.Balancing bike sharing systems with constraint programming[J].Constraints,2016,21(2):318-348. [3] NAIR R,MILLER-HOOKS E,HAMPSHIRE R C,et al.Large-scale vehicle sharing systems:analysis of Vélib’[J].International Journal of Sustainable Transportation,2012,7(1):85-106. [4] LATHIA N,SANIUL A,CAPRA L.Measuring the impact of opening the London shared bicycle scheme to casual users[J].Transportation Research,Part C:Emerging Technologies,2012,22:88-102. [5] 徐建闽,秦筱然,马莹莹.公共自行车多层次分区调度方法研究[J].交通运输系统工程与信息,2017,17(1):212-219. [6] BORGNAT P,ABRY P,FLANDRIN P.Shared bicycles in a city:a signal processing and data analysis perspective[J].Advances in Complex Systems,2011,14(3):1-24. [7] BORGNAT P,ROBARDET C,ABRY P,et al.A dynamical network view of Lyon’s Vélo’v shared bicycle system[M]//MUKHERJEE A,CHOUDHURY M,PERUANI F,et al.Dynamics on and of Complex Networks,Volume 2.Berlin,Germany:Springer,2013:267-284. [8] VOGEL P,MATTFELD D C.Strategic and operational planning of bike-sharing systems by data mining-a case study[C]//Proceedings of ICCL’11.Berlin,Germany:Springer,2011:127-141. [9] VOGEL P,GREISER T,MATTFELD D C.Understanding bike-sharing systems using data mining:exploring activity patterns[J].Procedia-Social and Behavioral Sciences,2011,20(6):514-523. [10] ETIENNE C,OUKHELLOU L.Model-based count series clustering for bike sharing system usage mining:a case study with the Vélib’ system of Paris[J].ACM Transactions on Intelligent Systems and Technology,2014,5(3):1-21. [11] CHARDON C M D,CARUSO G.Estimating bike-share trips using station level data[J].Transportation Research,Part B:Methodological,2015,78:260-279. [12] CHEN L,JAKUBOWICZ J,ZHANG D,et al.Dynamic cluster-based over-demand prediction in bike sharing system[C]//Proceedings of 2016 ACM International Joint Conference.New York,USA:ACM Press,2016:841-852. [13] KADRI A A,LABADI K,KACEM I.An integrated petri net and GA based approach for performance optimization of bicycle sharing systems[J].European Journal of Industrial Engineering,2015,9(5). [14] ZHOU X L.Understanding spatiotemporal patterns of biking behavior by analyzing massive bike sharing data in Chicago[J].PLOS One,2015,10(10). [15] JEH G,WIDOM J.SimRank:a measure of structural-context similarity[C]//Proceedings of the 8th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York,USA:ACM Press,2002:538-543. [16] 周文乐,朱 明,陈天昊.一种基于网站聚合和语义知识的电影推荐方法[J].计算机工程,2014,40(8):277-281. [17] 王 健,李志斌,林鸿飞.一种基于社会化标注的网页检索方法[J].计算机工程,2012,38(15):50-52. [18] 田 玲,曾 涛,陈 蓉,等.基于SimRank的中药“效-效”相似关系挖掘[J].计算机工程,2008,34(12):242-243.2 算法实现
2.1 基于连接关系的站点相似度矩阵
2.2 聚类过程
3 实验
3.1 实验结果与分析
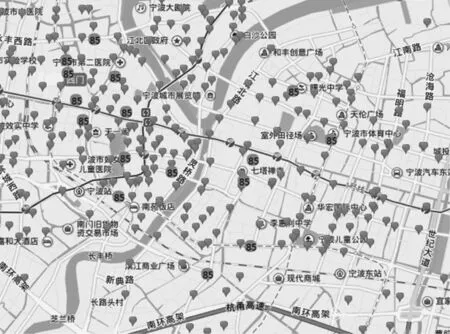
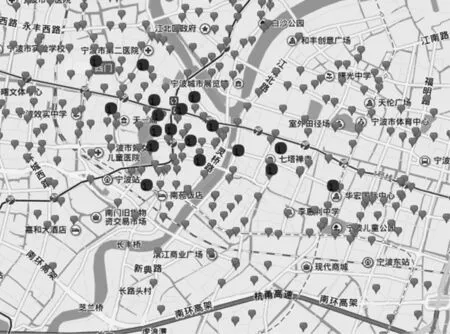

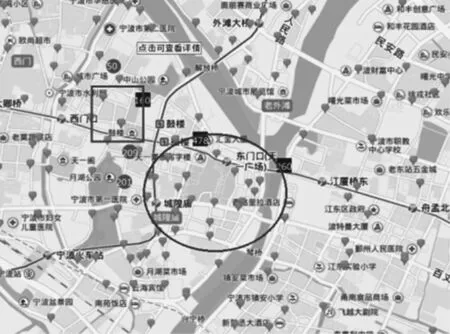
3.2 参数影响
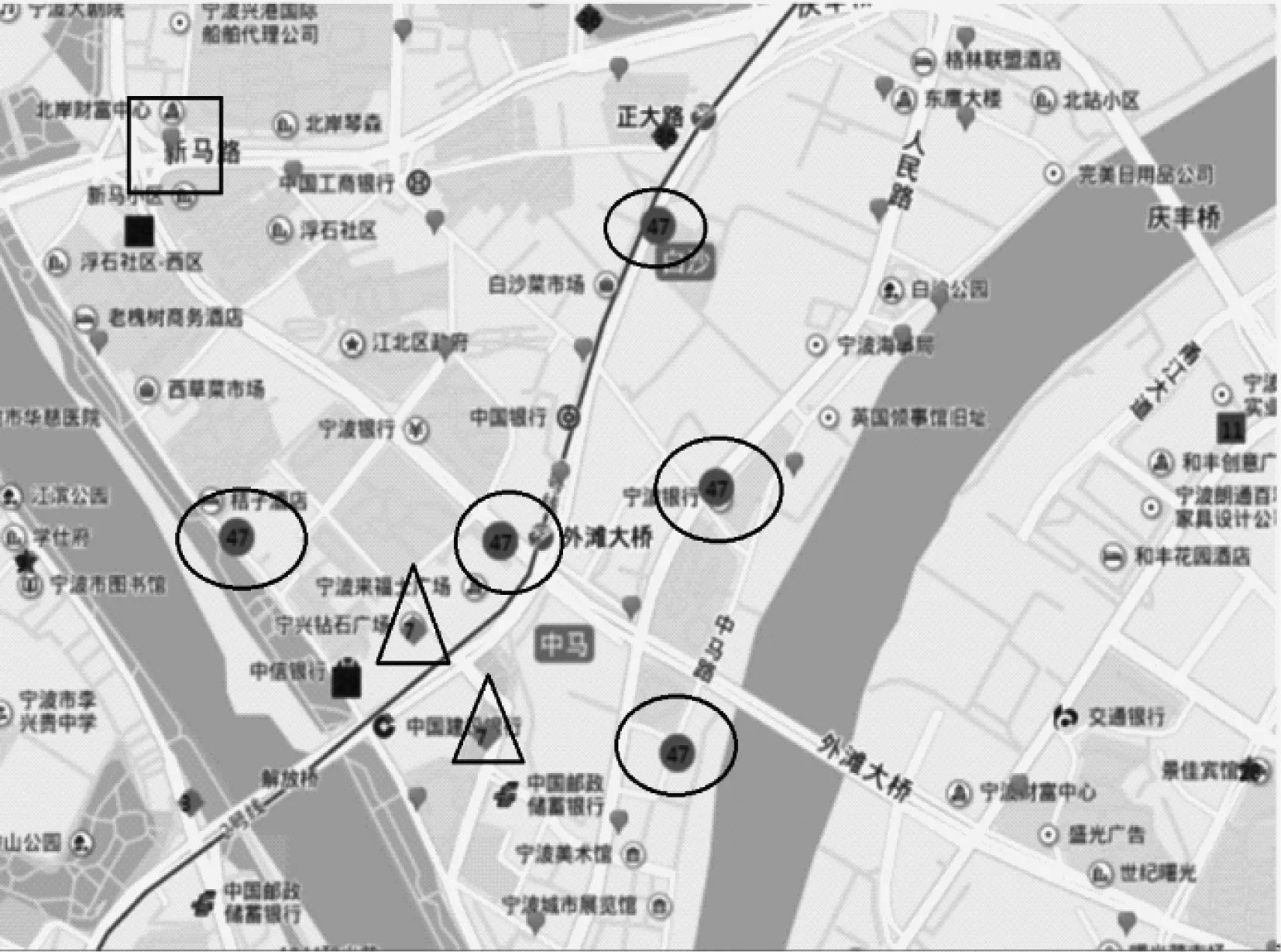
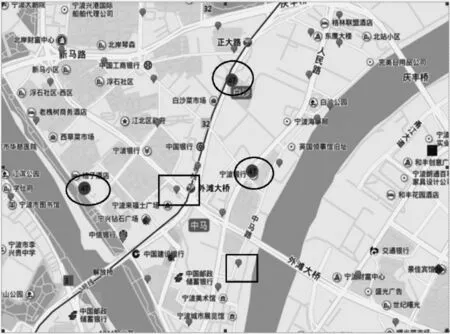
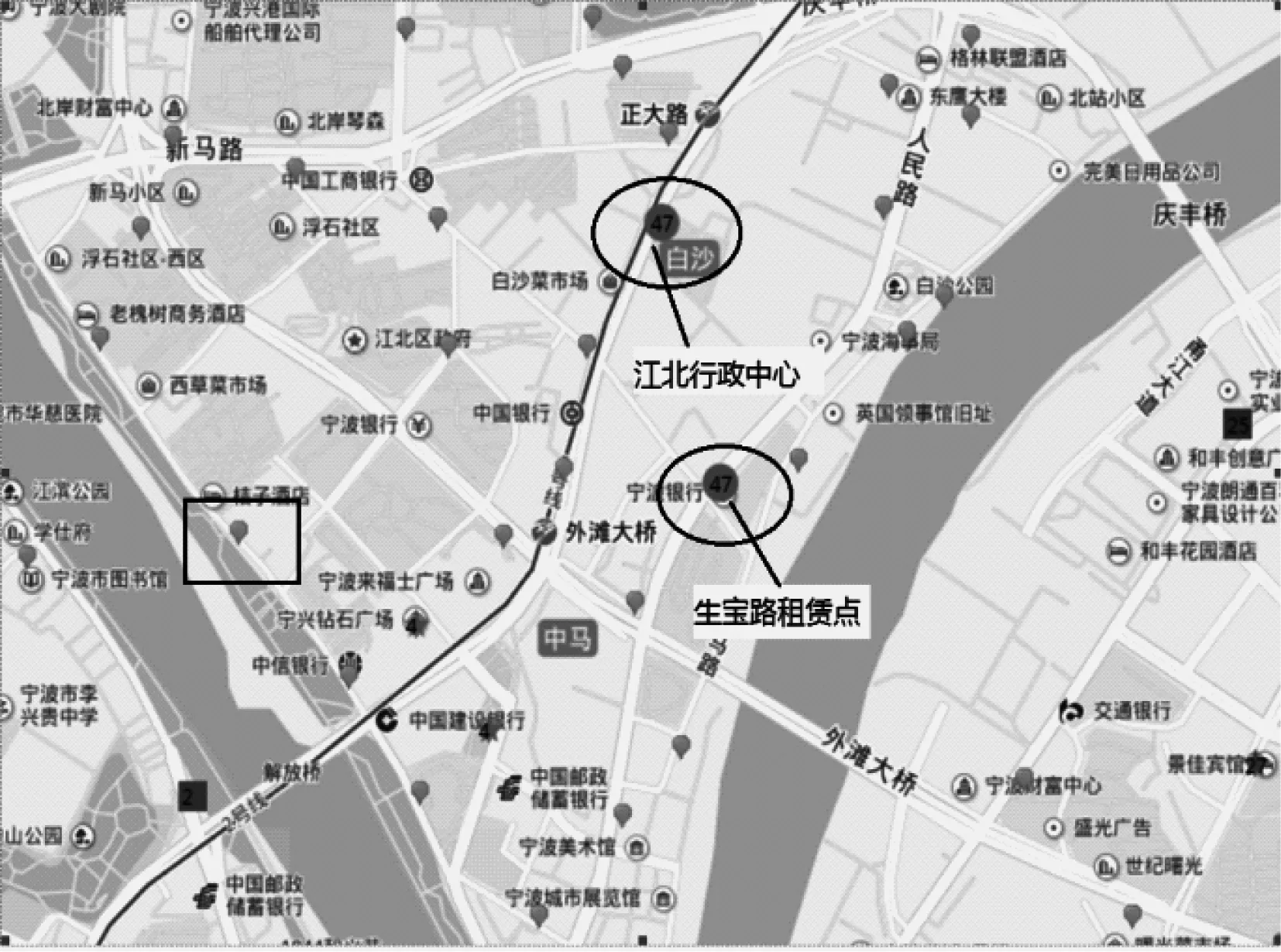
4 结束语

