两阶段业务排队模式选择研究

吴鑫锦

（山西大学经济与管理学院，太原030006）

无论在制造业还是服务行业中，一项完整作业有多个业务流程都很常见。对于一项作业有两个业务流程的排队模型，两窗口串联排队模型通过把业务合并，并保持窗口个数及服务人数不变，则可以使其转变为m/m/2并联排队模型。比如，药房买药，当业务分开办理时，顾客需要在缴费窗口排队进行缴费和记录，再到取药窗口排队取药；如果合并业务，并保持窗口个数及服务人数不变，使得两个窗口均可由服务员同时办理两个业务，顾客则只需排一次队，等待其中任意一个空闲窗口同时办理缴费和取药。不难发现，合并业务可以减少顾客排队次数，从而可能减短顾客逗留的时间；但不合并业务，则服务者的服务技巧因专业而日进，从而提高服务强度。如何决定两阶段业务合并与否是本文试图解决的问题。

感兴趣的是：相等的窗口个数和服务员人数，并已知各服务率μ，μi，（i=1，2）完成一样的业务，不同的模型是否有一样的顾客效用？为了描述决策过程，我们构建了顾客效用函数来对两模型进行比较。设顾客到达独立且服从参数为的泊松过程，服务原则为FCFS，顾客完成一次完整服务的收入为v，系统平均逗留时间Wis（i=1，2），单位逗留时间支出为d，整个服务收费为ki，（i=1，2）。标定一位顾客，建立效用函数：Ui=ν-ki-dWis，设无等待时间时，Ui恒大于 0。若 Ui≥0，（i=1，2），则顾客选择进入，若Ui＜0，则顾客选择离开。且0到μ之间存在唯一实际进入率λ，使得Ui=0。

令 U1=0，ν-k1-dW1s=0，代入 W1S得：λ3+αλ2+βλ+χ=0

由卡尔丹公式解一元三次方程得出，当定价为k1，允许最大进入强度为：

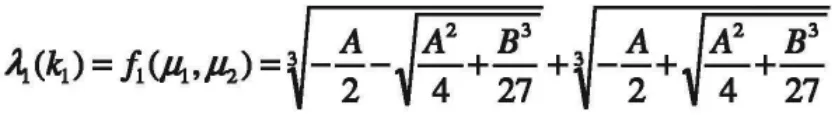
令U2=0有

得出定价为k2时最大进入强度为：若两模型定价相等，即k1=k2=k，基于服务率的变化对两类系统进行比较，我们可得到以下定理。定理1：Λ≥min{λ1（k），λ2（k）}时，当μ＜μ*时，顾客更愿意分开办理业务，当μ＞μ*时，合并业务；Λ≥min{λ1（k），λ2（k）}或μ=μ*时，业务合并和业务分开办理效果一致。证明：已知Λ，ν，d且定价相等k1=k2=k，则顾客进入模型一

令λ1（k）=λ2（k），即有：

（1）Λ≥min{λ1（k），λ2（k）}时，若μ＜μ*，则λ1（k）＞λ2（k），故有，顾客进入模型一的概率大。μ＞μ*顾客进入模型二的概率大。

（2）μ=μ*时，λ1（k）=λ2（k），故有，顾客进入系统的概率相等。

（3）Λ＜min{λ1（k），λ2（k）}时，两个模型都能满足所有顾客进入系统，顾客进入率都为1。

本文把两阶段业务的两种不同服务模式用串联排队和m/m/2并联排队分别体现，从对模型对照分析的角度来研究排队论中的决策问题，不仅可以突出模型之间的异同和优劣，也为公司决策提供理论参考，为管理者合理设置窗口提供优化建议。

参考文献：

[1]陆传赉．排队论[M]．北京：北京邮电大学出版社，2009．

[2]侯振挺，刘海芳．两服务台串联排队系统[D]．长沙：中南大学，2007．

[3]侯振挺，等．排队论中的马尔可夫骨架过程方法[J]．长沙铁道学院学报，2001，（1）．