中部六省国家可持续发展实验区创新能力评价研究——基于AHP和DEA的非均一化灰色关联方法

朱兆钰，刘胜男

（山西大学经济与管理学院，太原 030006）

引言

美国运筹学家T.L.Saaty等人在20世纪70年代提出了定性与定量分析相结合的层次分析法（AHP），其虽然能够充分利用专家的主观意见，却过分依赖专家的主观判断，从而可能会出现由于人为因素带来的评价偏差。数据包络分析（DEA）是运筹学家Charnes等人以“相对效率”概念为基础，根据多指标投入和多指标产出对相同类型的单元进行相对有效性评价的一种方法。该方法评价时虽不受人为因素的影响，但却无法反映决策者的偏好。灰色系统理论是我国著名学者邓聚龙教授于1982年提出的，其中的灰色关联分析是利用各方案与最优方案之间的关联度大小来对评价对象进行排序。该方法虽对样本量无严格要求，但在计算各方案与最优方案的关联度时使用同一组权重，不能体现评价的客观性。基于AHP和DEA的非均一化灰色关联分析方法以灰色关联分析为中心模型，通过AHP和DEA共同确定各方案的综合权重，再计算出各方案的关联度。该方法综合了上述三种方法的优势。本文通过这一方法对中部六省三种类型的实验区创新能力分别进行评价，以了解中部六省实验区创新能力的差距，从而为山西省实验区今后的发展提供一定的参考。

一、基于AHP和DEA的非均一化灰色关联方法

（一）基于AHP和DEA相结合的指标权重计算

首先运用传统的AHP法确定主观权重，接着运用DEA中的CCR模型获得非均一化的客观权重，最后引入主观偏好系数将获得的主客观权重通过线性加权的方式得到综合权重：

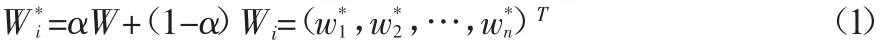
式中，W*i为第个决策单元的综合权重，α为主观偏好系数，1-α为客观偏好系数，α∈[0，1]，α由决策者根据偏好给出。

（二）基于AHP和DEA的灰色关联分析模型

首先基于成本型指标取值越小越好，效益性指标与之相反的原则确定最优方案指标集D0，接着运用极值法对评价矩阵进行规范化处理，然后根据式（2）求得第i个方案与第j个最优指标的关联系数εij：

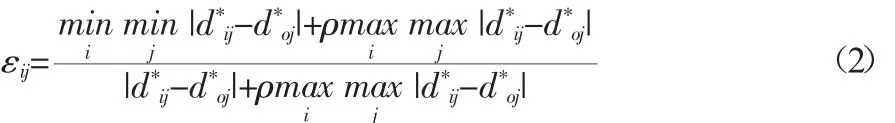
式中，ρ 为分辨系数，ρ∈[0，1]，一般取 ρ=0.5。由 εij可得关联系数矩阵E。

最后根据关联系数行向量Ei和W*i指标权重向量，可求得各方案的关联度Ri（i=1，2，…，m）。

关联度Ri越大，说明方案集Di与最优指标集D0越接近，因此可根据关联度的大小对方案进行优劣排序。

二、结果分析与评价

对中部六省县域型、城区型、地级市型三种类型的实验区的创新能力分别进行评价。从县域型评价结果来看，山西省的盂县排名第8，右玉县排名第11，怀仁县排名第21，泽州县排名第24。从数据来看，山西省的这四个实验区在本级科学技术支出所占比例、万人专利授权数、累计认定并有效的高新技术企业这三项指标上与最优指标集的关联度均低于0.45。整体看，本级科学技术支出所占比例普遍偏低，万人专利授权数较少，累计认定并有效的高新技术企业很少。此外，怀仁县在单位GDP能耗和亿元GDP生产安全事故死亡率指标上与最优指标集的关联度仅在0.46左右，表明该实验区单位GDP能耗和亿元GDP生产安全事故死亡率均偏高。而泽州县在单位GDP能耗指标上与最优指标集的关联度仅为0.333，表明其单位GDP能耗过高，在今后的发展过程中应当注意节能。

从城区型评价结果来看，山西省太原市迎泽区排名第5，朔州市朔城区排名第7。从数据来看，这两个实验区在万人专利授权数、累计认定并有效的高新技术企业及人均GDP三项指标上与最优指标集的关联度都在0.42以下。整体看，万人专利授权数相对较少，累计认定并有效的高新技术企业偏少，人均GDP普遍偏低。此外，太原市迎泽区空气质量达到二级以上天数占全年比重这一指标与最优指标集的关联度仅为0.333，可见其在环境方面应加强治理。朔州市朔城区亿元GDP生产安全事故死亡率与最优指标集的关联度仅为0.333，其在今后的发展过程中应当关注生产安全问题。

从地级市型评价结果来看，山西省长治市排名第5。从数据来看，长治市在本级科学技术支出所占比例、万人专利授权数、累计认定并有效的高新技术企业、人均GDP、单位GDP能耗、空气质量达到二级以上天数占全年的比重这6项指标上与最优指标集的关联度都在0.35以下。

通过中部六省三种类型的实验区创新能力的评价结果可以看出山西省的排名均靠后，其评价指标向量与最优指标集的关联度均较低，都处于实验区创新能力系统的边缘，区域创新能力较低。

参考文献：

[1]Satty T L．A scaling method for priorities in hierarchical structures．Journal of Mathematical Psychology，1978，1（1）：57-68．

[2]Satty T L．Axiomatic foundation for the analytic hierarchical process．Management Science，1986，23（7）：851-855．

[3]魏权龄．评价相对有效性的数据包络分析模型——DEA和网络DEA[J]．北京：中国人民大学出版社，2012：7-71．

[4]王先甲，张熠．基于AHP和DEA的非均一化灰色关联方法．系统工程理论与实践[J]．2011，31（7）：1222-1229．