观赏海棠花期性状与有效积温的关系

储吴樾, 张往祥,2, 范俊俊

(1.南京林业大学林学院，江苏 南京 210037；2.扬州小苹果园艺有限公司，江苏 扬州 225200)

物候学是研究自然界的动植物与环境条件(如气候、水文和土壤条件)周期性变化之间相互关系的科学，研究自然季节现象变化的规律，以服务于农业生产和科学研究[1].植物物候期对气候变化响应的研究越来越受到重视，在全球气候变化的研究中，物候常被认为是反映气候与环境变化的重要指标[2].随着遥感技术、数码技术、网络传输技术和地理信息系统等新技术的出现，物候观测的水平在进一步提升[3-4].物候学在区域分类[5]、植物育种[6]、病虫害防治[7]、农业产量预测[8]、景观变化与旅游[9]等方面得到了越来越广泛的应用.

园林绿地景观作为城市景观效果的重要组成部分，已成为城市窗口的一个重要展现载体，在园林设计中，合理地利用花期交错，能有效地搭配植物营造良好的观赏效果[9].相比于草本花卉，木本植物具有更高效、长远的生态效益花期物候，因此对木本花卉物候的研究具有重要意义[10].植株不同种(品种)基点温度不同[11]，准确有效的基点温度需要通过具体试验及计算，试验周期长且计算过程复杂[12].因此在植株的物候研究中，多数研究者根据文献资料，采用人为的设置方法对植株各发育阶段的基点温度进行推算，但无法区分品种间基点温度的差异[13].温度具有日变化特性，然而在大多数的积温研究中，积温的计算是基于日均温[14-15]，并未考虑温度的日变化，这使得有效积温的计算结果与真实值之间产生偏差.

本试验通过简化基点温度的计算方法并将结果采用有效积温累加的计算方式，对65个观赏海棠(Malus)品种的基点温度及始花期有效积温进行计算，通过分析积温与基点温度的特性，为观赏海棠的花期预测以及花期发育模型的建立提供参考.

1　材料与方法

1.1　试验地概况

试验地位于江苏省江都市仙女镇(东经119°55′，北纬32°42′)南京林业大学观赏海棠种质资源圃，属北亚热带季风气候，四季分明，年平均气温约14.9 ℃，年平均降雨量约1 000 mm，无霜期约320 d.试验地地势平坦开阔，各品种种植立地条件一致，土壤为沙壤土，土层深厚肥沃且灌排条件良好.

1.2　材料

供试观赏海棠品种共66个，其中的粉冠(M. ‘Pink Spires’)不参与分析(其初花期作为基准参数)，实际计算的品种为65个，其品种名称及序号如表1所示.所有品种皆引自美国，每个品种30株，按照2 m×3 m的株行距栽植，行间和株间未郁闭，光照充足，小气候条件一致.选取的材料为正常发育、成长5～8年，且能稳定开花结实3年以上的植株.

1.3　数据的测定与计算

1.3.1气象数据的获得气象数据均来自中国气象数据网(http://data.cma.cn/site/index.html)，包括日气温参数(日最高温度、日最低温度和日平均温度).在温度的日变化中，由于当发育阶段中某日的日均温等于植物的下限温度时，按有效积温统计则数值为零，而一天中会有一段时间的温度高于日均温，这一时段的温度对生长发育则是有效的，按活动积温统计该日对生长发育的温度数值就是该日的日均温，这对有效积温的计算有着重要的作用[13]，因此本试验使用每日最高温对基点温度进行计算.

1.3.2海棠品种初花期的判断观赏海棠的物候依照文献[16]的方法观测，观测时间为2013—2016年每日下午14:00之后(植物的各种物候现象通常在高温之后出现，14:00之后气温最高)，观测内容为初花期(当10%的植株上有少数花的花瓣展开时即为该品种的初花期).

1.3.3基点温度的计算基点温度的计算：每种植物都有一个生长发育的下限温度，低于下限温度时，植物便停止生长发育，但不一定死亡；高于下限温度时， 植物才能生长发育.一般采用直线回归法对基点温度进行计算[12].

由于植物的有效积温具有较强的稳定性[17]，且观赏海棠各品种的花期物候有一定的节律性[18].根据这些特征可知在多品种观赏海棠开花时，在品种之间初花期相隔的时间段内，两者之间的有效积温差值不变，据此推断在一定的时间段内，各品种与‘粉冠’之间的有效差积温值为固定值，且不随年份的改变而改变.根据以上结论得到公式(1).计算时，设待计算品种的基点温度为TX，将‘粉冠’的初花期日期设定为1，待计算品种的初花期日期为n，且‘粉冠’初花期日期至待计算品种每年的初花期日期时间段内，每日的温度为Ti.

(1)

代入该品种各年份的初花期日期及每日温度数据，解出方程，求出未知变量该品种的基点温度TX.以此方法计算出各品种观赏海棠的基点温度(‘粉冠’的基点温度使用直线回归法进行计算).

表1供试观赏海棠品种及序号Table 1　Names and No. of the tested ornamental crabapple cultivars

基点温度的校正：为了使简化后基点温度的计算结果与基点温度直线回归法的计算值更接近，本试验选取部分品种依据直线回归法对其结果进行验证并对简化后的计算方法所计算出的结果进行校正(本试验依据观赏海棠花期开花节律特性，随机从早、中、晚花期品种群[10]中各选取3个品种，分别为‘芭蕾舞’、‘红衣主教’、‘春之颂’、‘雪堆’、‘爱丽’、‘金黄蜂’、‘珊瑚礁’ 、‘金丰收’、‘黄油果’.

1.3.4有效积温的计算有效积温指作物在某时期内有效温度的总和.张福春[19]应用积分回归法对北京春季的树木开花期与它前期气象因子的关系作了统计学分析，指出春季气温对开花期的早迟具有决定作用，因此，本试验选取春季气温作为有效积温的计算数据.根据张宝堃[20]的候温确定季节划分的方法，连续5天(候)温度稳定在10 ℃以上，则春季开始.因此，本试验将有效积温起始日期(t1)定为连续5天(候)温度稳定在10 ℃以上后的第一天.有效积温指的是植株从发育的起始日期至结束日期ti之间的温度累积值.本试验使用有效积温累加的方法[如公式(2)所示]计算各品种观赏海棠的有效积温，当日最高温度大于基点温度时即为有效积温，当小于基点温度时，当日有效积温为0.公式(2)中，设待计算品种的初花期日期为ti，起始日期至初花期日期之间每日最高气温为T，该品种当年有效积温为S.

(2)

计算出历年的积温，将历年的积温进行平均求得该品种的有效积温，以此方法计算出各品种的有效积温.

1.3.5观赏海棠的品种编码及有效积温次序的建立依据观赏海棠4年的初花期起始日期顺序，分别按年将各品种划分为早花期、中花期和晚花期品种群[10].4年都处在早花期组群的品种编码设定为1；3年在早花期组群，1年在中花期组群的品种编码设定为2；2年在早花期组群，2年在中花期组群的品种编码设定为3；3年在中花期组群，1年在早花期组群的品种编码设定为4；4年在中花期组群的品种编码设定为5；2年在晚花期组群，2年在中花期组群的品种编码设定为6；3年在晚花期组群，1年在中花期组群的品种编码设定为7；4年都为晚花期组群的品种编码设定为8.根据有效积温的计算结果，将各品种按有效积温的大小进行排序.

2　结果与分析

2.1　基点温度的计算结果

将‘芭蕾舞’、‘红衣主教’、‘春之颂’、‘雪堆’、‘爱丽’、‘金黄蜂’、‘珊瑚礁’、‘金丰收’和‘黄油果’等9个品种的初花期物候数据与温度数据分别代入直线回归法[12]及简化后的计算方法进行计算，分别计算得出9个品种的基点温度直线回归法计算值及简化后的基点温度计算值(图1).

y1为基准线；y2为简化后基点温度计算值；a为简化后基点温度计算值与基准线之间的差值，a=1.901 1.图1　简化后基点温度计算值与回归法计算值的对比Fig.1　The comparison between biological zero temperature value and the calculation value with regression method

将两组计算值与使用直线回归法计算所得的基点温度值进行拟合后发现，简化后基点温度的计算结果与直线回归法计算所得的结果具有极显著差异(P<0.01)，且两组计算值之间的平均误差值为1.901 1 ℃(图1).根据上述的对比结果，对公式(1)进行校正，求出校正后的基点温度TX1为：TX1=TX+1.901 1[校正后的计算结果与原计算方法所得结果的相关系数为0.998(P<0.01)，且标准偏差为0.21].

对比后发现，校正后的计算结果与原计算方法所得结果较为接近[相关系数为0.998(P<0.01)，且残差值υ=-0.2～0.6].因此，可采用简化并校正后的基点温度的计算方法求出各品种的有效积温.

2.2　有效积温的类群划分

将校正后计算所得的各品种观赏海棠的基点温度TX1代入公式(2)中，得出各品种2013—2016年的平均有效积温值(图2).

参照花期区域时序顺序，发现开花较早的品种多数分布在品种编码1～2之间，中花期品种多数分布在品种编码3～6之间(‘黄油果’除外)，晚花期品种多数分布在品种编码7～9之间(‘绣球’、‘金黄蜂’除外).参考此结果，将观赏海棠分为低有效积温品种(1～2，25.28～145.46 ℃)、中有效积温品种(3～5，151.16～225.40 ℃)和高有效积温品种为(6～8，311.66～448.76 ℃).其分布如图2所示.

2.3　有效积温与基点温度的关系

从图3可以看出，整体而言，各品种观赏海棠的有效积温与其生物学阈值成呈指数递减关系(y=3 618.5e-0.242x，R2=0.969 6)，即随着基点温度的升高，有效积温降低.基点温度为5～12 ℃的品种(主要为中积温和高积温品种)，其数值离散性较大，耦合度低(y1=1 699.2e-0.171x，R2=0.789 3)；基点温度为12～20 ℃的品种(为低积温品种)，其数值耦合度极高(y2=2 994.6e-0.265x，R2=0.982 2).

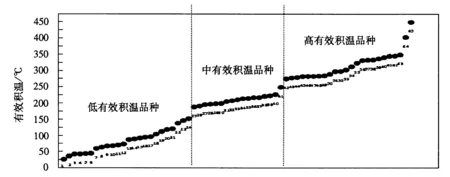
图2　观赏海棠品种群花期有效积温时序Fig.2　Ornamental crabapple varieties groups divided by effective accumulated temperature

y为全部品种的基点温度；y1为编码3～9品种的基点温度；y2为编码1～2品种的基点温度；虚线位置为基点温度分界线(x=13).图3　观赏海棠有效积温与基点温度的关系Fig.3　Relationship between effective accumulated temperature and biological zero temperature in ornamental crabapple

2.4　有效积温对初花期日期的影响

图4显示，各品种观赏海棠的平均初花期与有效积温之间呈线性关系(y=0.027 9x+31.997)，但两者间的耦合度较低(R2=0.602 3).有效积温与每年初花期日期之间呈显著相关性，但相关系数较低 (r2013年=0.764，r2014年=0.723，r2015年=0.728，r2016年=0.671).

为了计算的简便，将初花期起始日期转换为距离3月1日的实际天数,得到各初花期的时间序列.如3月1日为数值1，3月2日为数值2，以此类推，将4年各品种的初花期日期进行平均，求得平均初花期日期.图4　观赏海棠品种间有效积温与初花期日期的关联性Fig.4　The relationship between effective accumulated temperature and initial flowering date in ornamental crabapple

3　讨论

3.1　基点温度计算结果的评价

温度具有日变化特性，而在积温研究中，大多数积温的计算是基于日均温[14-15]，导致积温的计算会出现偏差.因此，本试验在计算有效积温的过程中，采用每日最高温进行计算，弥补原有计算方法的不足.

传统的基点温度计算方法采用对假定值进行回归分析的方法，此计算方法繁杂，且需要多年数据的支持，基点温度的计算效率较低[21-22]，这样会使得预测模型的计算耗时费力.根据植株有效积温变化度较小，且生物学阈值具有稳定性等特点[15]，对原有的积温计算方法进行简化，将计算结果进行累加即为植株的有效积温，计算所得值与原计算方法的结果相似(校正后计算的结果与原计算方法所得结果的相关系数为0.998(P<0.01)，且标准偏差为0.21)，且避免了计算过程中对基点温度的假定及回归分析，提升了运算速率，减少了因为假定值的设定而产生的误差.由于本试验采用了多品种观赏海棠作为计算参照物，研究结果可能具有一定的局限性，但此方法的运用对未来木本花卉基点温度计算方法的简化提供了一个思路.

3.2　有效积温计算结果及区域划分

本试验通过代入各品种观赏海棠的基点温度进行累加的计算方法计算出植株的有效积温，并对各品种进行积温次序的排列及编码，以探究各品种之间积温的联系，并对各品种有效积温与初花期之间的关联性进行研究，之后对各品种的有效积温进行区域划分.结果表明，各品种之间有效积温的差异性较大，这可能源于不同品种原产地环境各不不同，为了适应原产地环境，满足其生物量需求，各品种的有效积温与基点稳定温度发生了变化；另一方面由于各品种多为杂交产生[20]，品种杂交后，由于外来基因的加入使得植株原有的遗传特性发生改变，造成与母株的有效积温产生差异.

单一品种的有效积温是无法代表所有品种的有效积温，而现阶段大多数植株的花期预测模型中，并没有针对各品种特点进行模拟计算[9,23]，这会导致物候预测模型的计算结果产生偏差，从而对花期模拟的准确性降低.在观赏海棠有效积温的区域划分中，参照花期时序品种群，综合初花期时序，可以将观赏海棠品种分为高、中、低有效积温品种.通过对有效积温计算结果的区域划分，可以准确判断各品种积温之间的关联性，为确准建立多品种观赏海棠花期模型提供参考.

3.3　有效积温与基点温度的关联性

前人[10, 23]研究表明，花期长短是遗传因素与环境因素共同作用的结果.过低的冬、春季温度会使花期缩短[24]，反之会使花期加长[25].将有效积温结合基点温度进行分析的结果(图2)显示，观赏海棠高、中有效积温品种群的有效积温与基点温度的离散性较大，且耦合度较低(R2=0.789 3)，而低有效积温品种群的离散性较小，耦合度极高(R2=0.982 2)，表明高于基点温度12 ℃的品种(低有效积温品种)，其花期时序稳定性大于中、高有效积温品种，且初花期日期及时序变化受外界影响较小.此外，有效积温为5～12 ℃的品种，其聚集度较大，有效积温较为接近.在对比观赏海棠4年的初花期日期顺序中发现，中、高有效积温品种相对于低有效积温品种发生区域“跳跃”的频率更大.

据此推断：有效积温由遗传因素与环境因素共同影响，相比于中、高有效积温品种，低有效积温品种更容易受遗传因子的影响，且在基点温度<12 ℃时，遗传因子的影响力远远大于环境因子.由此可见，在未来花期模型的建立中，相对于中、高有效积温品种，多数利用有效积温建立的花期预测模型更适用于低有效积温品种群，且在基点温度<12 ℃的情况下，低有效积温品种群花期预测的准确性更高.因此，对于多数观赏海棠品种而言，采用单一的预测模型进行计算，并不能有效地对多数观赏海棠品种进行准确预测，这就需要在未来的观赏海棠花期预测过程中，应针对品种的差异而采用多种预测模型进行预测.

3.4　有效积温与初花期日期的关联性

本试验对观赏海棠有效积温与初花期日期之间的关联性进行研究，发现有效积温与初花期呈显著的相关性，但相关系数较低(r2013年=0.764，r2014年=0.723，r2015年=0.728，r2016年=0.671).表明有效积温对初花期有着一定的影响，但初花期并不完全由有效积温决定，因此仅仅通过有效积温对初花期进行模拟计算，其精确度还有待考究.但另一方面，多数预测模型的建立立足于气候条件[21-27]，在前人的研究中，温度作为影响初花期的主要因素，一旦计算中的温度低于植物的基点温度，对于初花期日期的影响就大大降低，就会导致未来花期预测模型的准确率降低.因此，在模型的建立中，将植物的有效积温作为一个重要因子代入预测模型中，对预测模型精度的提升有着显著作用，这为未来的花期预测模型的建立提供了参考.

[1] 竺可祯,宛敏渭.物候学[M].北京:科学出版社,1980.

[2] 陈效逑,张福春.近50年北京春季物候的变化及其对气候变化的响应[J].中国农业气象,2001,22(1):2-6.

[3] 李胜强,张福春.物候信息化及物候时空变化分析[J].地理科学进展,1999,18(4):352-359.

[4] 葛全胜,戴君虎,郑景云.物候学研究进展及中国现代物候学面临的挑战[J].中国科学院院刊,2010,25(3):310-316.

[5] 赵明伟,岳天祥,孙晓芳,等.基于草地综合顺序分类系统(IOCSG)的中国北方草地地上生物量高精度模拟[J].生态学报,2014,34(17):4 891-4 899.

[6] HUINE I, BELMONTE J, MIGNOT A. A modelling analysis of the genetic variation of phenology between tree populations [J]. Journal of Ecology, 2000,88(4):561-570.

[7] SUN J. Dynamic monitoring and yield estimation of crops by mainly using the remote sensing technique in China [J]. Photogramm Eng Remote Sen, 2000,66(5):645-650.

[8] 蒋菊芳,梁从虎,杨华,等.近十年气温和降水对荒漠植物梭梭、刺蓬物候期的影响[J].干旱区资源与环境,2017,31(2):141-146.

[9] 王言鑫,张增信,杨艳蓉,等.南京市77种常见木本植物花期特征分析[J].南京林业大学学报(自然科学版),2014，38(5):118-122.

[10] 张往祥,魏宏亮,江志华,等.观赏海棠品种群的花期物候特征研究[J].园艺学报,2014,41(4):713-725.

[11] JOHN R P. Temperatures and the growth and development of wheat: a review [J]. European Journal of Agronomy, 1999,10:23-36.

[12] 王炳赟,范广洲,魏鸣,等.基于温度影响因子的植物物候模型的应用研究[J].生物数学学报,2015，30(2):253-262.

[13] 吴玉洁,叶彩华,姜会飞,等.不同积温计算方法作物发育期模拟效果比较[J].中国农业大学学报,2016,21(10):117-126.

[14] 张菲,邢小霞,李仁杰,等.利用地温构建菏泽牡丹花期预测模型[J].中国农业气象,2008，29(1):87-89.

[15] 韩小梅,申双和.物候模型研究进展[J].生态学杂志,2008,27(1):89-95.

[16] 刘秀珍,宛敏渭.中国物候观测方法[M].北京:科学出版社,1987.

[17] MCMASTER W W, WILHELM G S. Growing degree-days: One equation, two interpretations [J]. Agriculturul and Forest Meteorology, 1997,87(4):291-300.

[18] 魏宏亮.观赏海棠开花节律特征研究[D].南京:南京林业大学,2015.

[19] 张福春.北京春季的树木物候与气象因子的统计学分析[J].地理研究,1983，2(2):55-64.

[20] 张宝堃.中国季节之分布[J].地理学报,1934,1(1):1-18.

[21] 鲁小珍,叶镜中,孙多.带输入项的线性自回归模型在树木物候预测中的应用[J].浙江林学院学报,1998，15(2):201-206.

[22] 沈竞,张弥,肖薇,等.基于改进SW模型的千烟洲人工林蒸散组分拆分及其特征[J].生态学报,2016,36(8):2 164-2 174.

[23] 陆佩玲.中国木本植物物候对气候变化的响应研究[D].北京:北京林业大学,2006.

[24] 陈翔高,房伟民,汪诗珊,等.梅花开花物候期及加长观赏期的研究[J].北京林业大学学报,1999，21(2):23-27.

[25] 胡安生,管彦良,蒋斌芳,等.高温胁迫下温州蜜柑内源乙烯和脱落酸的释放及其与落花落果的关系[J].中国农业科学,1993,26(6):12-16.

[26] 张震,丁乃千.梨花花期与产量的相关性及产量预报模型[J].贵州农业科学,2015，43(4):158-162.

[27] 刘占林,宋颐,李珊,等.华山新麦草开花物候期观测和自然种群基因流的间接估测[J].植物生态学报,2001,25(4):426-430.