面向邻近目标分辨的MIMO雷达波形设计方法

柏婷, 郑娜娥, 李海文

(信息工程大学数据与目标工程学院, 450001, 郑州)

邻近距离目标分辨问题是雷达领域的研究热点,在编队飞行器、舰船的探测方面具有重要价值[1],距离分辨性能较差易导致严重检测误差。影响邻近目标分辨能力的主要因素是距离分辨力和距离模糊函数旁瓣的大小,距离分辨力由发射信号带宽决定,直接影响最小可分辨距离。距离旁瓣(RSL)过高会导致邻近目标分辨中弱目标淹没、不同目标主旁瓣混叠的情况。通过对雷达的发射波形进行设计可提高距离分辨力、抑制距离旁瓣,提高发射波形的固有分辨能力,有利于接收端进行匹配滤波。由于正交频分复用(OFDM) MIMO雷达具有波形分集和频率分集能力,在高分辨和参数估计方面优势显著[2],且对OFDM MIMO信号进行相位编码调制,能获得低RSL的发射波形[3],因此OFDM MIMO雷达的波形设计在邻近目标分辨方面潜力巨大。

然而,OFDM MIMO雷达系统作为一种多载波调制系统,存在功率峰均比(PAPR)过高的问题,直接影响实际系统的运行成本和效率[4]。目前,通信领域提出了许多功率峰均比的抑制方法,大致可分预失真技术、编码类技术和加扰类技术[5-6]。然而,这些方法无法直接运用到雷达系统中,一是由于通信系统和雷达系统对于功率峰均比的阈值要求不同;二是通信系统对误码率性能的要求很高,但雷达侧重于考虑不同场景下功率峰均比抑制方法对参数估计性能的影响。因此,针对邻近目标分辨问题,在保证信号RSL特性的前提下,设计低功率峰均比的发射波形是本文研究的重点。

文献[7]采用非支配排序遗传算法NSGA-II对时域信号包络峰均比和距离模糊函数峰值旁瓣比进行联合优化,该方法减小了频谱的带外泄漏,但是峰均比降低程度有限;Sebt等人通过时域序列循环移位寻找功率峰均比最低序列,再对该序列进行时域削峰(Clipping),循环操作直至得到期望值[8],该方法计算复杂度小,且能有效降低功率峰均比,但频谱和距离模糊函数失真严重。文献[9]在子载波预留法的基础上,以优化包络变化系数为目标函数,采用最小二乘法进行求解。该方法可以直接求出解析解,故复杂度极低,但是在功率峰均比抑制和RSL性能方面都有所欠缺,不适用于精度要求高的情况。Wang等人运用Clipping结合自适应滤波的方法对功率峰均比进行抑制[10],RSL和功率峰均比性能均能达到较好水平,但该方法的运算复杂度较高。

基于上述技术背景,针对现有方法存在的缺陷,本文提出了一种基于序列二次规划法(SQP)的波形设计方法。首先,建立针对高分辨场景的OFDM MIMO雷达发射信号模型;其次,以最小化功率峰均比为目标函数,最大距离旁瓣电平(MSL)和距离模糊函数包络变化因子(CVE)为约束构造优化问题;最后,运用SQP方法求解该优化问题,设计优化波形。本文方法可同时获得良好的功率峰均比和RSL性能,并可根据系统需求对方案配置参数进行适当调整。仿真分析结果验证了本文方法的有效性。

1　信号模型

假设OFDM MIMO雷达系统的收发天线均采用等间距均匀线阵,收、发天线同步,发射天线数为M。设sm(t)为第m根天线上[0,T]时间内发射的OFDM信号,其子载波数为N,发射脉冲持续时间为T,则sm(t)的表达式为

(1)

式中:Sm(q)是第m根天线上第q个子载波的编码;Δf为子载波之间的频率间隔,为保证子载波间正交性,有Δf=1/T,S=[S1,S2,…,SM]∈CN×M是所有天线上的编码序列矩阵,Sm=[Sm(1),Sm(2),…,Sm(N)]T,编码序列采用PCM调制方式,即Sm(q)=ejφm(q),m=1,…,M,q=1,…,N,相位参数为φm(q)。令采样率fs=1/Ts=NΔf,则时间离散的OFDM信号为

(2)

第m个阵元发射信号示意图如图1所示。

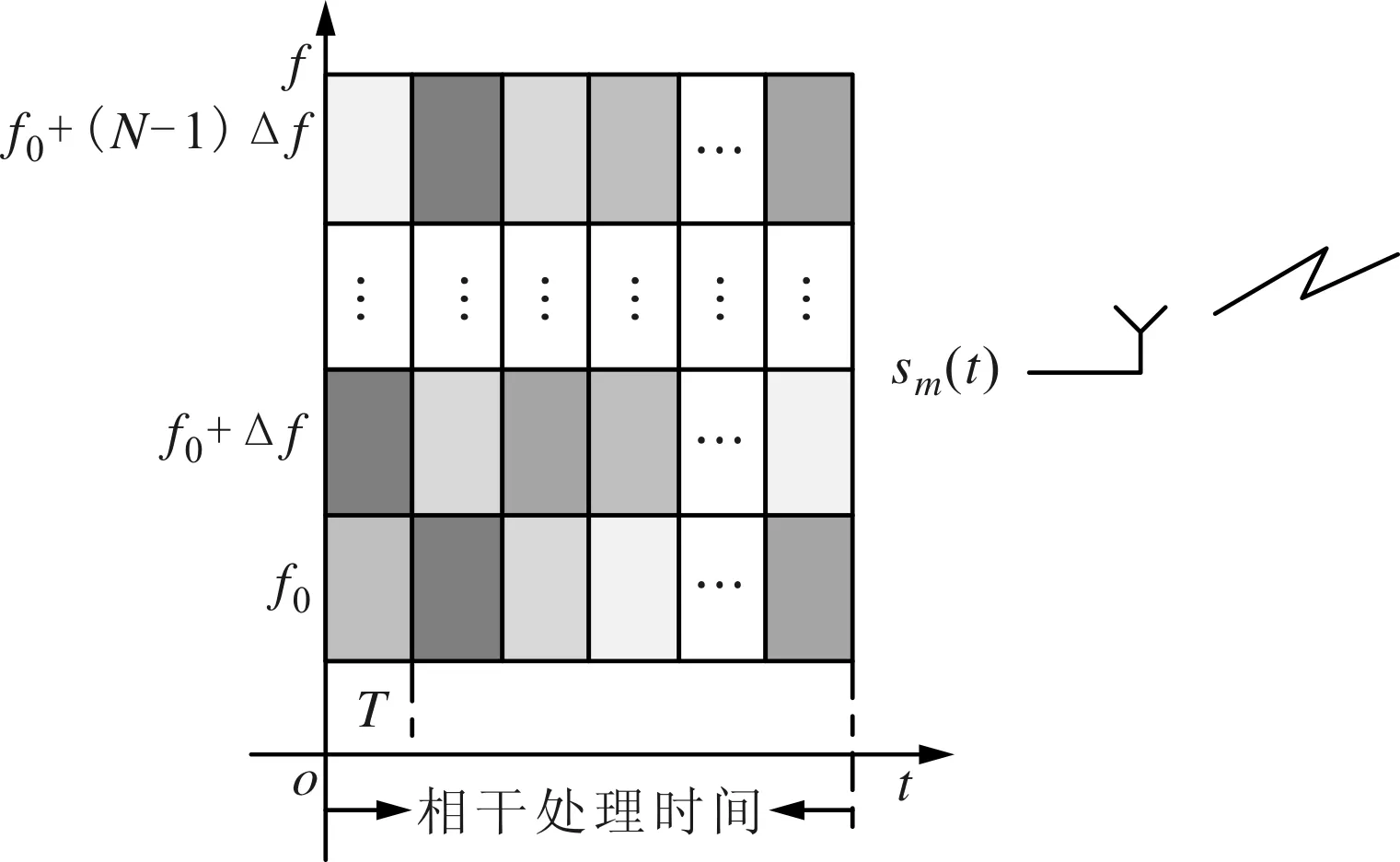
图1　第m个阵元发射信号示意图

2　波形设计方法

2.1　目标函数的建立

发射信号的功率峰均比定义为[11]

rPAPR=maxn|sm(n)|2/E[|sm(n)|2]

(3)

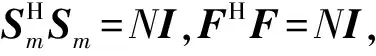
(4)

故最小化功率峰均比的目标函数可表示为

(5)

若只考虑降低功率峰均比这单一指标,而不考虑其他指标的影响,会影响系统的实际应用。故本文针对邻近目标分辨问题,在降低功率峰均比的同时,结合影响分辨效果的RSL性能建立优化模型。距离模糊函数是衡量雷达发射波形性能的重要参数之一,距离模糊函数旁瓣越低,越有利于解决邻近目标分辨中弱目标淹没和不同目标主旁瓣混叠的问题。在此,引出距离模糊函数的定义[12]

(6)

本文从两方面入手保证发射信号的RSL性能。一是引入包络变化因子来表征优化前后距离模糊函数旁瓣整体包络的变化,其定义为

(7)

式中:cCVE为CVE的幅值;χ0(k)表示初始序列距离模糊函数。对CVE进行限定,即可对整体旁瓣变化进行约束。二是限定最大距离旁瓣水平mMSL=max|χ(k)|,以防止距离模糊函数旁瓣整体抬升。据此,在保持RSL特性条件下最小化功率峰均比的优化问题可以表示为

(8)

式中:mMSL为MSL的幅值;α、β分别表示不同应用场合下的最大可允许距离旁瓣值和包络变化因子,可以根据初始序列的特征选取适当值。

2.2　基于序列二次规划法的求解算法

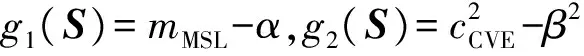
(9)

(10)

(11)

式中

[ej2πn/N,ej2π2n/N,…,ej2πn]T

(12)

由以上分析和公式,最终可得如下优化步骤。

(1)选取初始编码序列SN×1,对称正定矩阵H0∈RN×N.根据初始序列功率峰均比和距离模糊函数旁瓣值设定α,β,并给出截止条件,当f(i)≤γ时,迭代终止。其中,f(i)为第i次迭代时的目标函数值,令i=0。

(2)在S(i)处求解f(i),若有f(i)≤γ,则循环结束,转入步骤(6);否则,求解式(13)的二次规划得到迭代方向的最优解向量d(i)

(13)

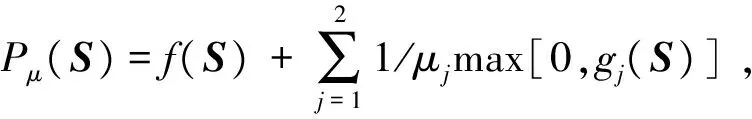
(4)利用拟牛顿法更新矩阵H,得到

(14)

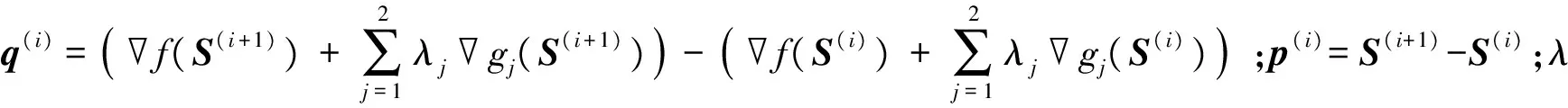
(5)令i=i+1,返回步骤2。

(6)同理,求出此天线其余脉冲的编码和时域序列,并利用COD方法解出其余天线的发射信号。

根据上述步骤,即可求出优化后的波形序列。

2.3　算法收敛性能与复杂度分析

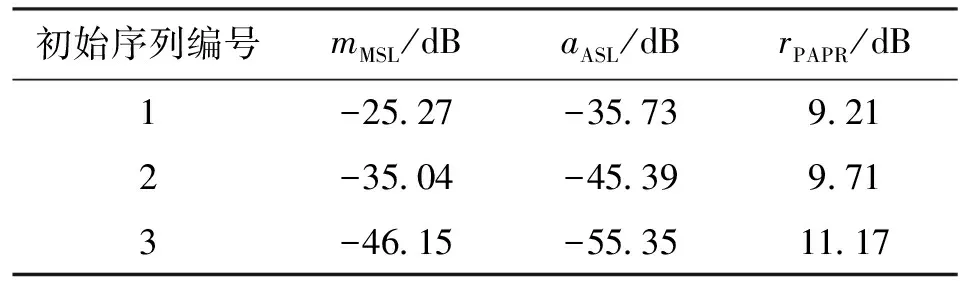
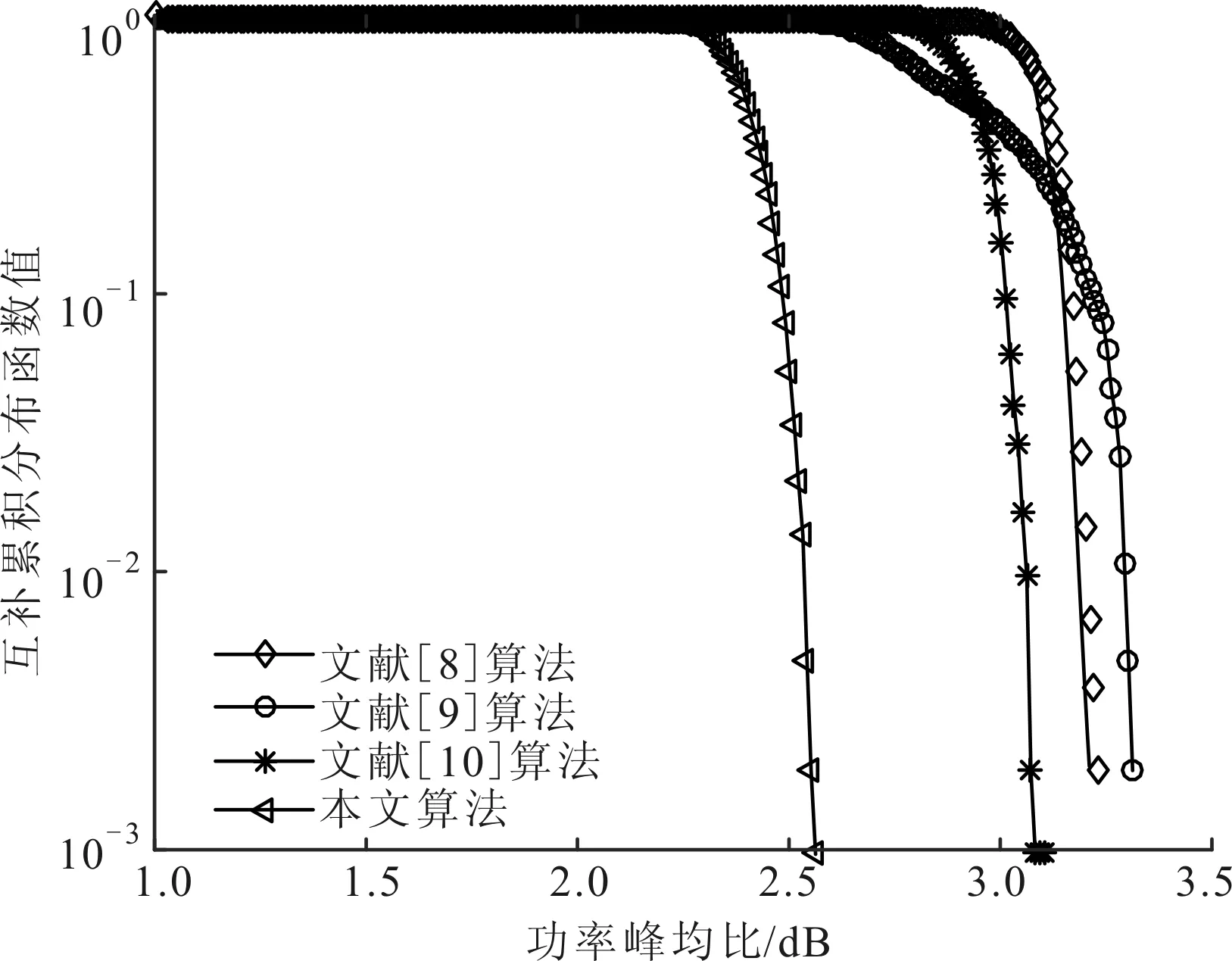
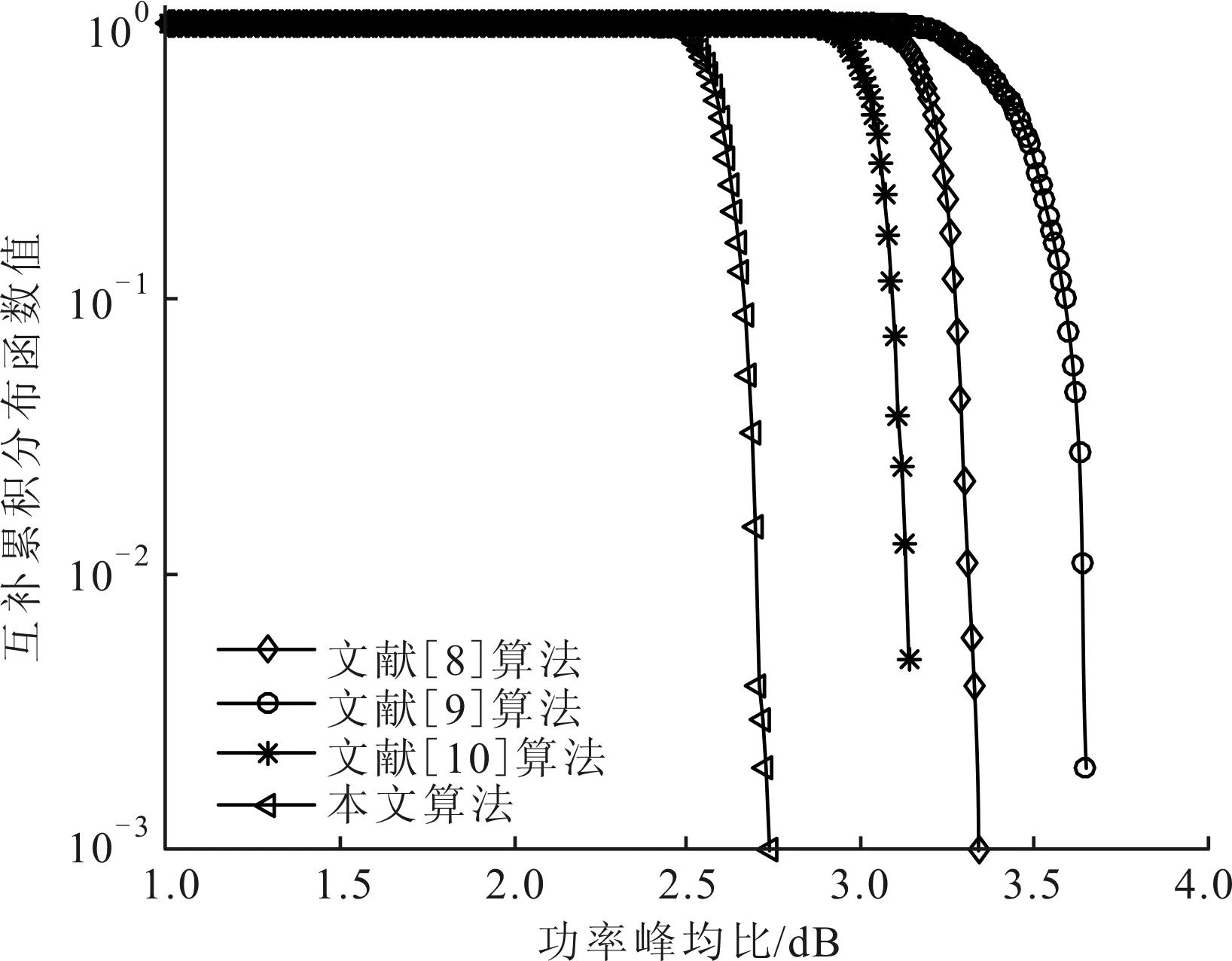
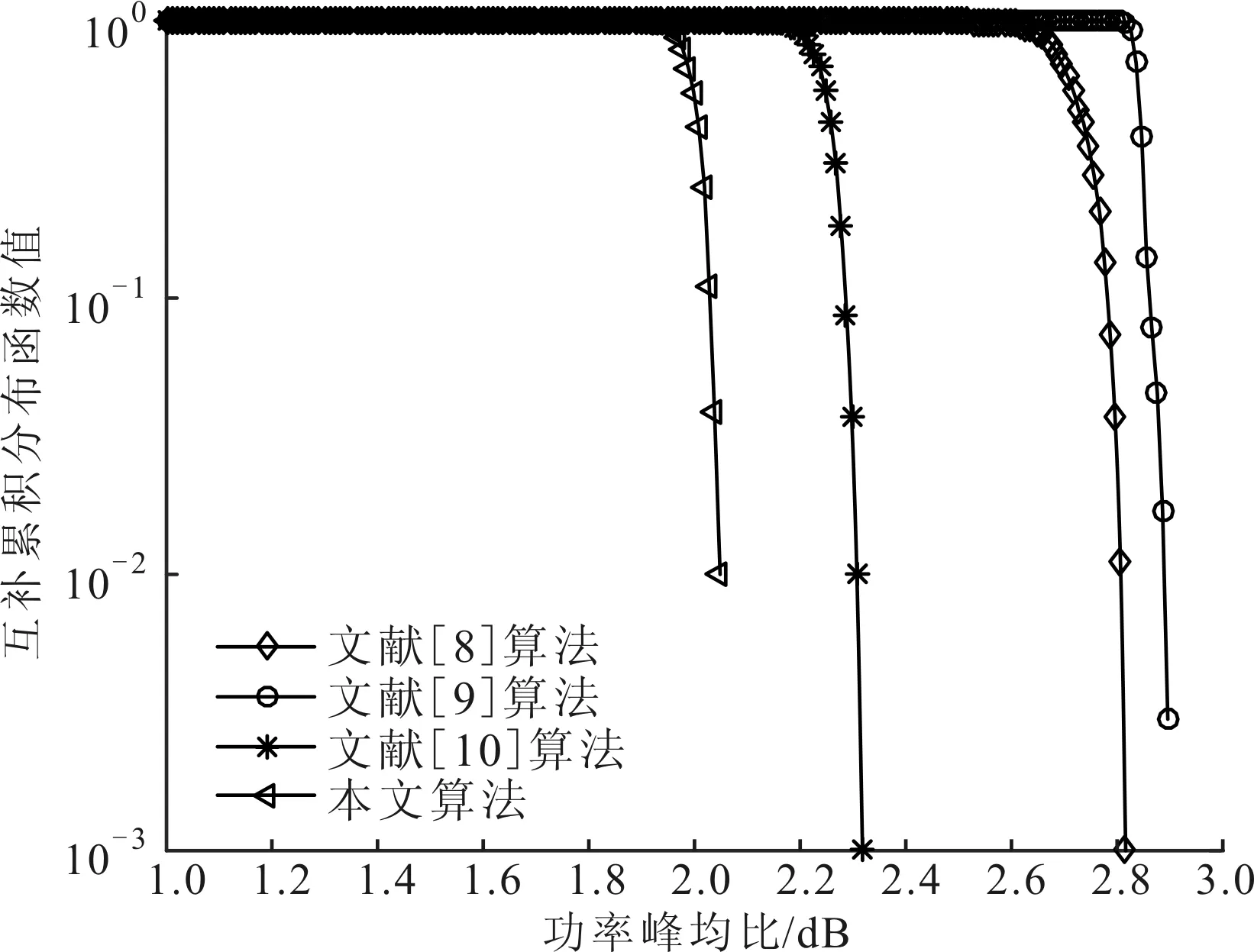
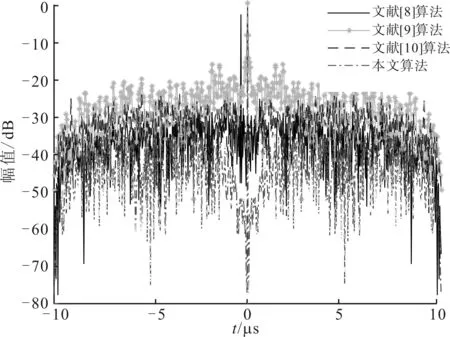
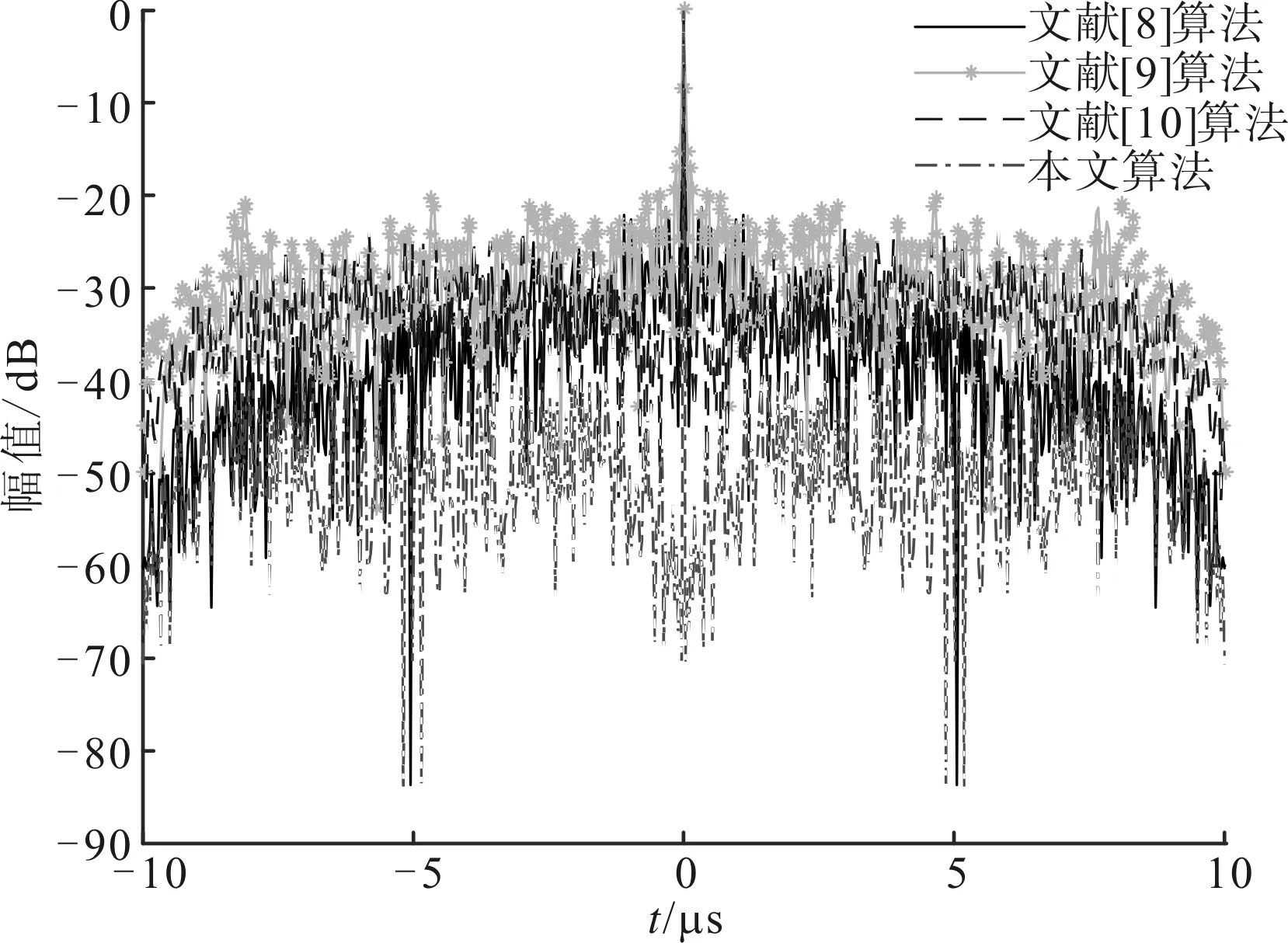
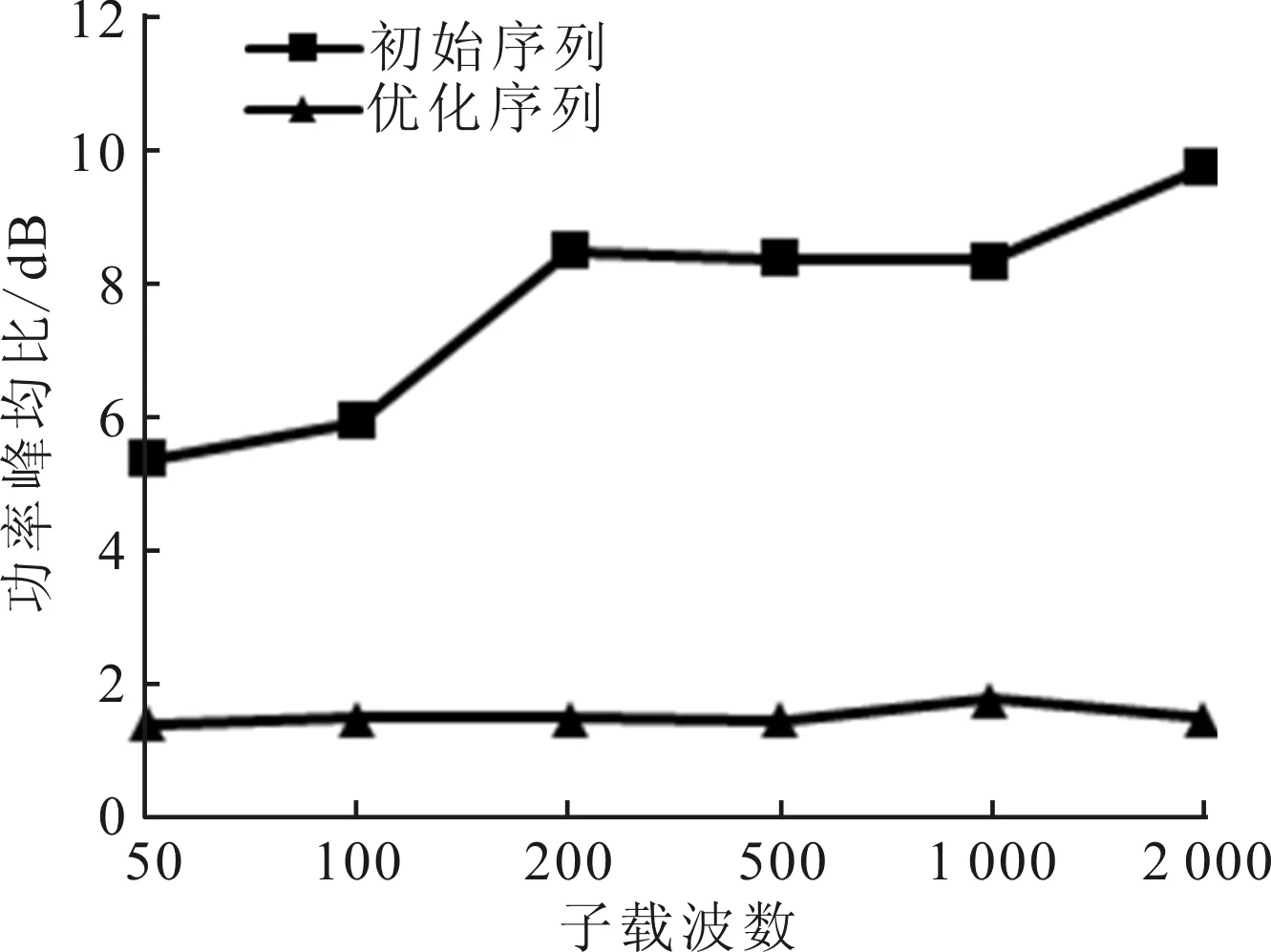
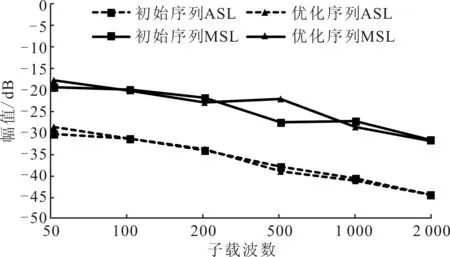
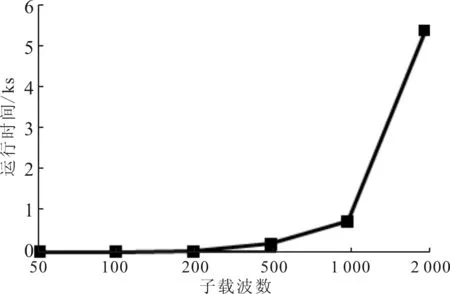
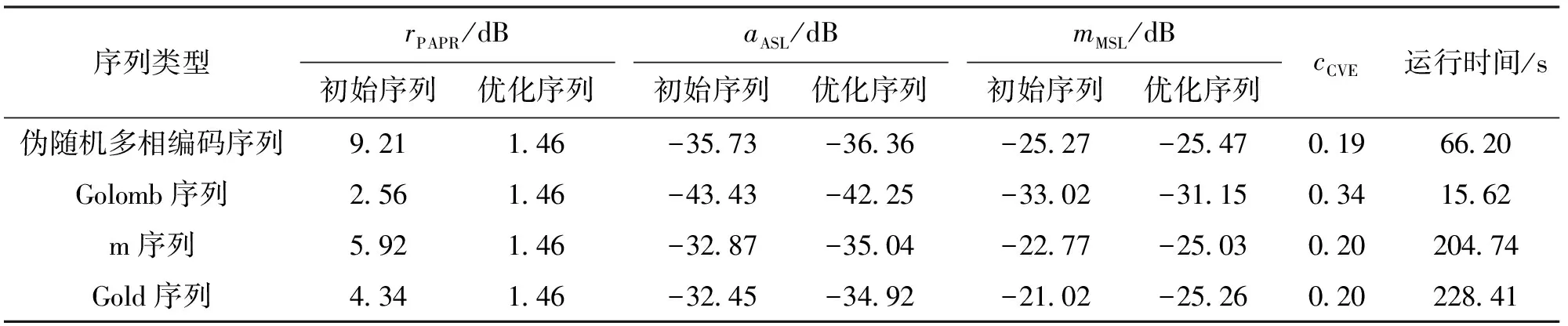
对约束优化问题式(9),f,gk(k=1,2)均连续可微,则有常数0

(15)

表1比较了本文算法和文献[8-10]算法的复杂度。可以看出,文献[8-9]算法的运算复杂度较低,文献[10]算法的运算复杂度较高。本文算法的主要计算量为迭代操作,在每次迭代中计算式(10)的复杂度约为O(NlbN),式(11)的复杂度约为O(N2),式(12)的复杂度约为O(N2),其他计算复杂度较低,故本文算法总的复杂度约为O(N2+NlbN)。可以看出,本文算法相对复杂度较高,但在实际应用中也可接受。

表1　4种算法的复杂度比较

3　实验仿真

本节的仿真实验考虑M=4的OFDM MIMO雷达系统,脉冲持续时间T=10 μs,带宽B=30 MHz,子载波间隔Δf=1/T=0.1 MHz,载波数N=B/Δf=300。为了定量描述功率峰均比的降低程度和RSL性能,采用功率峰均比(dB)、互补累计分布函数(CCDF)[5]、CVE、平均距离旁瓣电平(ASL)、运行时间作为算法评价指标。其中,CCDF定义为OFDM符号的功率峰均比超过某一门限值z的概率

P{rPAPR>z}=1-P{rPAPR≤z}=1-[1-e-z]N

(16)

实验1测试本文算法性能。选取MSL、功率峰均比和ASL各异的3组编码序列作为初始序列,其参数值见表2。由表2可以看出,3组序列的MSL和ASL分布较均匀,具有一定代表性,但其功率峰均比值均较高。对于α,β的取值,需综合考虑初始序列的MSL大小mMSL和波形包络情况,初始取值范围为mMSL,0≤α≤0,0≤β≤1。在此范围内,选取表3中(α,β)值的组合对算法进行100次蒙特卡洛测试。对同一初始序列的所有参数组合测试结果进行比较,从中选出功率峰均比和ASL最好的参数组合,结果见表4。由表4可见,本文算法对功率峰均比的降低效果显著,所有序列均能达到2 dB以下,序列1和2达到了1 dB以下,满足雷达系统要求[8]。同时,序列的RSL性能损失较小,控制在7%以内,序列1的RSL性能甚至有所提升。由此可见,本文算法在降低功率峰均比和保持RSL特性方面效果良好。

值得指出的是,(α,β)的取值并不完全决定优化后序列的旁瓣状态,实验中得出的最优值(αopt,βopt)和其他(α,β)值得到的ASL差值都保持在3 dB以内,功率峰均比差值均不超过0.3 dB,所以在实际系统中,(α,β)的取值并不需要强制固定,依据初始序列指标合理选择即可。

表2　初始序列参数值

实验2测试不同算法性能。选择实验1中的3组序列及其最优参数(α,β)作为初始序列和参数,文献[8-10]中的算法作为对比算法,由文献[8]可知,当rPAPR<2 dB时,符合雷达发射放大器要求,故本节算法的截止条件为rPAPR=2 dB。图2给出了3组序列经过不同算法优化后的CCDF性能,优化后的距离模糊函数旁瓣性能比较见图3,综合性能比较结果见表5。

从图2和图3可以看出,本文算法在不同初始序列下的CCDF性能和RSL性能均最优。由表5可知,初始序列RSL越深,对比算法的性能越差,而本文算法在不同初始序列条件下的表现均较好。值得指出的是,虽然表5中文献[8]算法的ASL性能良好,但其距离模糊函数在靠近主瓣附近旁瓣抬升明显(见图3),因此在邻近目标分辨应用中有较大局限性。

表3　约束条件取值

表4　本文所提算法最优性能值

表5　不同算法性能比较

(a)序列1

(b)序列2

(c)序列3图2　3种序列的互补累计分布函数性能比较

实验3检验不同序列长度对算法的影响。分别选取长度为N=50,100,200,500,1 000,2 000的伪随机序列作为初始序列进行优化,其对应的距离分辨

力为R=30,15,7.5,3,1.5,0.75 m,因(α,β)取值对实验结果影响较小,故采用序列1的最优参数值,设置α=-15 dB,β=0.4。由于功率峰均比随子载波数逐渐变大,故考虑N=2 000时的各项参数指标,当截止rPAPR<2 dB后,截止功率峰均比越小,耗时增长越快,但ASL和MSL的变化都在1 dB以内,CVE基本不变。均衡各项参数指标后将截止条件取为rPAPR=1.46 dB,图4给出了优化效果的对比情况。由图4可以看出,子载波数的变化不影响本文算法的性能,对于不同子载波数的序列,其功率峰均比均能达到期望值,且RSL性能保持良好。算法的运行时间随着子载波数的增大而增大,当N>1 000时,运行时间增速明显提高。

(a)序列1

(b)序列2

(c)序列3图3　距离模糊函数性能比较

(a)对功率峰均比性能的影响

(b)对平均距离旁瓣电平的影响

(c)对运行时间的影响图4　子载波数对算法性能的影响

实验4检验不同初始序列对算法性能的影响。本文选择了不同类型的相位编码序列作为初始序列[18]进行对比,包括Golomb序列、m序列、Gold序列和伪随机多相编码序列。设置子载波数N=300,α=-15 dB,β=0.4,截止条件为rPAPR=1.46 dB。观察优化结果和初始序列的关系,结果见表6。

表6　初始序列类型对算法的影响

可以看出,初始序列的相位编码方式对rPAPR抑制和RSL保形的效果影响不大,所以本文算法对初始序列的选择依赖性不大。

4　结　论

本文提出了一种针对邻近目标分辨场景的OFDM MIMO雷达波形设计方法,能够有效兼顾雷达发射信号的RSL和功率峰均比性能,并保持了信号的高分辨特性。该方法利用了SQP算法进行优化求解,仿真结果表明,优化后的发射波形功率峰均比达到了较低水平,符合实际系统工作要求,而且针对不同初始序列采用不同参数,以保证更好的抑制性能。同时,相对现有算法,本文抑制方法对信号的RSL性能影响较小,能保证更好的邻近目标分辨性能。对于不同子载波数、不同初始序列,本文算法均能保持良好性能,在实际应用中适用性较强。

参考文献:

[1]SUN B, CHEN H, ZOU H. Sparsity-aware multitarget localisation for distributed MIMO radar against phase synchronisation mismatch [J]. LET Communications, 2016, 10(17): 2269-2275.

[2]XIA X G, ZHANG T, KONG L. MIMO OFDM radar IRCI free range reconstruction with sufficient cyclic prefix [J]. IEEE Transactions on Aerospace & Electronic Systems, 2015, 51(3): 2276-2293.

[3]HUO K, ZHAO J J. The development and prospect of the new OFDM radar [J]. Journal of Electronics & Information Technology, 2015, 37(11): 2776-2789.

[4]赵越, 王腾, 陶然, 等. FrFT-OFDM系统的低复杂度峰均功率比抑制技术研究 [J]. 电子与信息学报, 2014, 36(1): 246-249.

ZHAO Yue, WANG Teng, TAO Ran, et al. Low complexity PAPR reduction method in FrFT-OFDM system [J]. Journal of Electronics and Information Technology, 2014, 36(1): 246-249.

[5]杨昉, 何丽峰. OFDM原理与标准: 通信技术的演进 [M]. 北京: 电子工业出版社, 2013: 40-49.

[6]胡武君, 杨霖. MIMO-OFDM系统中基于循环移位和信号联合的改进SLM算法 [J]. 通信学报, 2015, 36(4): 170-177.

HU Wujun, YANG Lin. Modified SLM algorithm based on cyclic shift and signal combination in MIMO-OFDM system [J]. Journal on Communications, 2015, 36(4): 170-177.

[7]LELLOUCH G, MISHRA A K, INGGS M. Design of OFDM radar pulses using genetic algorithm based techniques [J]. IEEE Transactions on Aerospace & Electronic Systems, 2015, 52(4): 1953-1966.

[8]SEBT M A, SHEIKHI A, NAYEBI M M. Orthogonal frequency-division multiplexing radar signal design with optimised ambiguity function and low peak-to-average power ratio [J]. IET Radar Sonar & Navigation, 2009, 3(2): 122-132.

[9]HUANG T, ZHAOT. Low PMEPR OFDM radar waveform design using the iterative least squares algorithm [J]. IEEE Signal Processing Letters, 2015, 22(11): 1975-1979.

[10] WANG Y C, LUO Z Q. Optimized iterative clipping and filtering for PAPR reduction of OFDM signals [J]. IEEE Transactions on Communications, 2011, 59(1): 33-37.

[11] WANG S H, LEE K C, LI C P. A low-complexity architecture for PAPR Reduction in OFDM systems with near-optimal performance [J]. IEEE Transactions on Vehicular Technology, 2016, 65(1): 169-179.

[12] 丁鹭飞. 雷达原理 [M]. 北京: 电子工业出版社, 2015: 381-390.

[13] 马昌凤. 最优化方法及其Matlab程序设计 [M]. 北京: 科学出版社, 2010: 180-215.

[14] 李占利. 最优化理论与方法 [M]. 北京: 中国矿业大学出版社, 2012: 129-132.

[15] ANDREI N. Sequential quadratic programming (SQP) [M]. Berlin, Germany: Springer-Verlag, 2017: 96-102.

[16] SCHITTKOWSKI K, YUAN Y X. Sequential quadratic programming methods [M]. Hoboken, NJ, USA: John Wiley & Sons Inc., 2011: 147-224.

[17] HE H. Waveform design for active sensing systems: a computational approach [M]. Gainesville, FL, USA: University of Florida, 2011: 19-23.