已加工表面热源模型研究及磨削温度场数值模拟
王德祥, 孙树峰, 颜丙亮, 刘新福, 江京亮
(1.青岛理工大学机械工程学院, 266520, 山东青岛; 2.山推道路机械有限公司研究院, 272103, 山东济宁)
磨削加工需要极高的能量比,绝大部分能量都在磨削区转化为热量[1]。磨削加工时传入工件的热量会在工件表层产生高温以及极大的温度梯度,导致工件产生热损伤。磨削温度场是研究磨削热损伤的重要依据。
随着计算机技术的快速发展,数值模拟技术成为研究磨削温度场的重要方法。利用计算机进行磨削温度场的数值模拟,需要建立磨削温度场的数值仿真模型。磨削温度场的数值仿真模型可以分为浅磨模型和深磨模型[2],如图1所示。浅磨模型不需要建立砂轮和工件接触表面与工件已加工表面之间楔形区域的几何模型,直接将热源施加到已加工表面上;深磨模型需要建立楔形区域的几何模型,并且需要划分极为精细的网格,而楔形区域内的网格一般具有较大的长宽比,容易导致计算结果不准确[2]。因此,浅磨模型更加方便,常用于磨削温度场的数值模拟。已加工表面热源的分布形状是进入工件已加工表面的热流密度分布,是利用浅磨模型研究磨削温度场的重要基础。目前,在利用浅磨模型进行磨削温度场的数值模拟时,一般把已加工表面热源的分布形状假设为直角三角形[3]、三角形[4]、抛物线[5]和椭圆[6]等形状。但是,已加工表面热源的分布形状会随着磨削工艺条件改变,上述假设都是基于特定的磨削工艺条件,不能普遍适用于所有的磨削工况。

(a)浅磨模型 (b)深磨模型图1 磨削温度场数值仿真模型
本文基于圆弧热源模型、砂轮和工件接触表面直角三角形热源,计算了被磨工件的无量纲磨削温度场,利用温度匹配法进行了反传热分析,建立了已加工表面热源分布形状的计算方法,采用有限元方法建立了磨削温度场的数值仿真模型(浅磨模型),仿真计算了工件的磨削温度场,并同实验结果进行了对比。
1 已加工表面热源分布形状计算方法
1.1 无量纲磨削温度场计算
由于磨削区未变形切屑厚度沿砂轮和工件接触表面趋于线性分布,并且磨削热流密度与未变形切屑厚度几乎成正比[7]。因此,砂轮和工件接触表面热源的分布不会随着磨削工艺条件改变,接近于直角三角形分布,如图2所示。

图2 工件磨削区的热源分布
在计算已加工表面热源的分布形状时,首先建立如图2所示的直角坐标系,然后基于圆弧热源模型[8]、砂轮和工件接触表面直角三角形热源,计算被磨工件的无量纲磨削温度场。无量纲磨削温度场的表达式为
(1)
式中:vw是工件速度;α是工件材料的热扩散率,且α=k/(ρc),k、ρ和c分别是工件材料的热导率、密度和比热容;qw是传入工件的平均热流密度;T(x,z)是工件的磨削温度场;lc是磨削接触弧长,且lc=(aeds)1/2,ae是磨削深度,ds是砂轮直径;λ是积分变量,表示接触表面上任意一点;φi是接触表面上任意一点处的接触角,且λ=dsφi;K0是零阶二类修正贝塞尔函数;f(λ)是描述接触表面热源分布形状的形函数,对于直角三角形热源,其形函数为
f(λ)=-2λ/lc
(2)
1.2 已加工表面热源的形函数计算
(3)
式中:[xa,xb]是已加工表面热源的分布区域;s(ω)是描述已加工表面热源分布形状的形函数;ω是积分变量,表示已加工表面热源分布区域内的任意一点。
在计算已加工表面热源的形函数时,首先将已加工表面热源的分布区域等分为m个区间,然后利用温度匹配法[10]进行反传热分析,可得以下方程组
(4)

(5)
式中:ωi和ωi+1是第i个区间的积分下限和积分上限,表述为
(6)
最后,对式(4)进行数值求解,即可得到描述已加工表面热源分布形状的形函数s(ω)。

图3 已加工表面热源的分布形状
在不同的磨削工艺参数下,将求得的已加工表面热源分布形状绘于图3,图中vs是砂轮转速。由图3可得,已加工表面热源的分布形状随着磨削工艺条件而改变,将已加工表面热源的分布形状假设为某一特定形状,并不适用于所有的磨削工况。因此,在利用浅磨模型对磨削温度场进行数值模拟时,必须根据具体的磨削工艺条件,计算相应的已加工表面热源分布形状。
2 磨削温度场数值仿真模型
本文采用有限元模拟软件ANSYS 14.0建立磨削温度场的数值仿真模型(浅磨模型),如图4所示,具体的建模过程如下所述。
2.1 几何模型及网格划分
在建立数值仿真模型时,建立了工件的二维几何模型。工件的长度是60 mm,高度是12 mm。为了方便加载热源,工件已加工表面的网格尺寸划分为磨削接触弧长的1/30。沿工件的高度方向,划分了30个网格,并且已加工表面附近的网格划分得更加细密。以上网格划分已通过网格独立性验证,足以获得准确的计算结果。单元类型选择二维八节点平面热效应单元PLANE77。
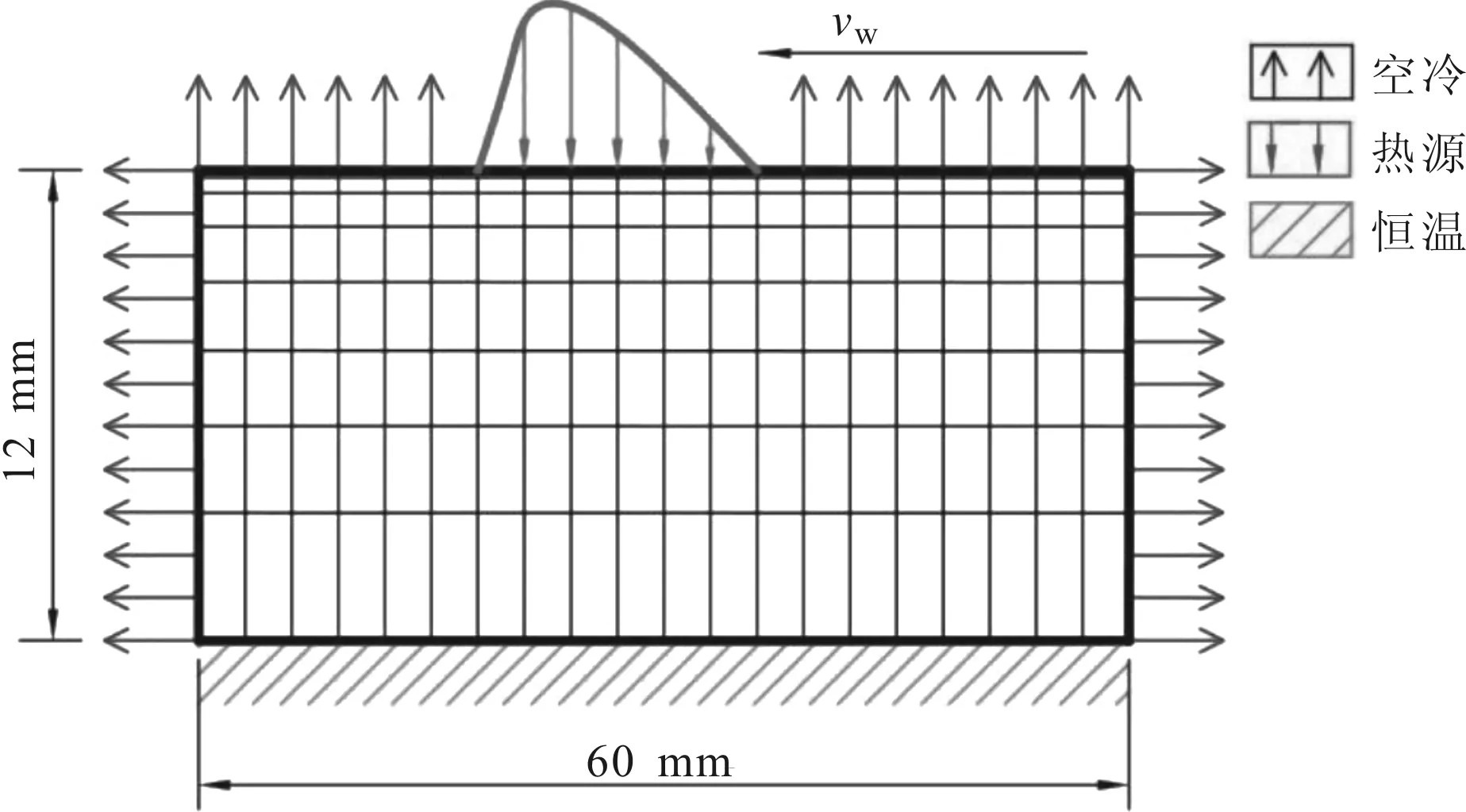
图4 磨削温度场数值仿真建模示意图
2.2 材料特性
工件材料是淬硬轴承钢GCr15,砂轮磨粒材料是白刚玉,两种材料的热物性参数如表1所示。
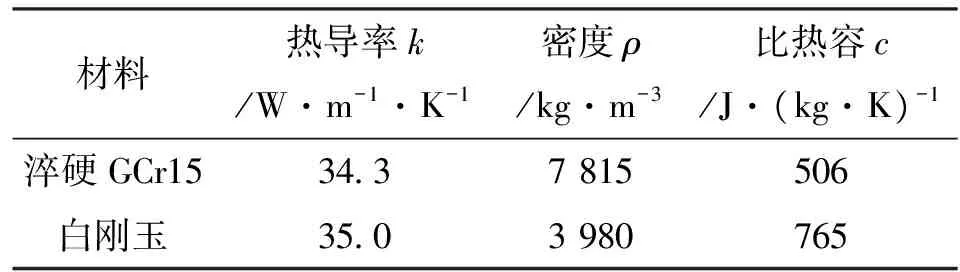
表1 两种材料的热物性参数[11]
注:文献[11]中的工件材料是AISI 52100,其材料特性接近于GCr15;白刚玉的热物性参数用于计算砂轮与工件之间的热量分配比。
2.3 边界条件
在建立数值仿真模型时,将周围环境温度设置为20 ℃,将工件底面设置为恒温绝热。干磨时,由于工件与周围环境之间的对流换热系数在20~100 W/(m2·K)之间,并且磨削温度场的数值仿真模型对对流换热系数的微小变化不敏感,因此将对流换热系数设置为60 W/(m2·K)[12]。
在模拟工件的磨削温度场时,将已加工表面热源加载到工件的已加工表面上,如图4所示。在计算已加工表面热源的热流密度分布qwf(ω)时,首先通过磨削实验测量切向磨削力Ft,再利用式(7)计算砂轮和工件接触表面上的平均热流密度
q=Ftvs/(blc)
(7)
式中:b是磨削宽度。
然后分析磨削区热量分配关系,计算砂轮与工件之间的热量分配比ε[11]和传入工件的平均热流密度qw,并且qw=εq,ε的表达式如下

(8)
式中:kg是磨粒的热导率;ro是磨粒接触半径。
最后计算描述已加工表面热源分布形状的形函数s(ω),并最终得到已加工表面热源的热流密度分布qwf(ω)=qws(ω)。
在计算已加工表面热源的热流密度分布qwf(ω)时,算得的形函数s(ω)实际上是m个离散值,并且只有ω∈[-lc,0]内的s(ω)离散值参与计算qwf(ω)。因此,算得的qwf(ω)也是一系列的离散值。在进行数值模拟时,将qwf(ω)的离散值施加到已加工表面热源分布区域内的节点上。由于沿工件的长度方向网格尺寸划分为磨削接触弧长的1/30,那么在已加工表面热源分布区域内有31个节点,因此算得的qwf(ω)应有31个离散值。为了获得31个qwf(ω)离散值,在计算形函数s(ω)时,假设已加工表面热源的分布区域为[-3lc,2lc],并将已加工表面热源的分布区域等分为150个区间,即m=150。
在数值模拟过程中,已加工表面热源沿磨削方向步进,并随时更新已加工表面的对流换热条件。
3 磨削力与磨削温度测量实验
采用MKL7120×6 CNC强力磨床开展平面磨削实验,磨削工艺条件如表2所示。在每次磨削之前,都进行砂轮修整。采用YDXM-III97型测力仪测量磨削力,采用Ti32型热成像仪测量磨削温度,磨削力与磨削温度测量实验的示意图[12]如图5所示。在测量磨削温度时,设置热成像仪的成像像素为320×240,空间分辨率为1.25×10-3rad,最小焦距为15 cm。

图5 磨削力与磨削温度测量实验示意图[12]
4 结果及讨论
根据如表2所示的磨削工艺条件,开展磨削力与磨削温度测量实验,计算传入工件的平均热流密度qw与已加工表面热源的形函数s(ω),并对工件的磨削温度场进行数值模拟。切向磨削力Ft的实验测量结果与平均热流密度qw的计算结果如表3所示。
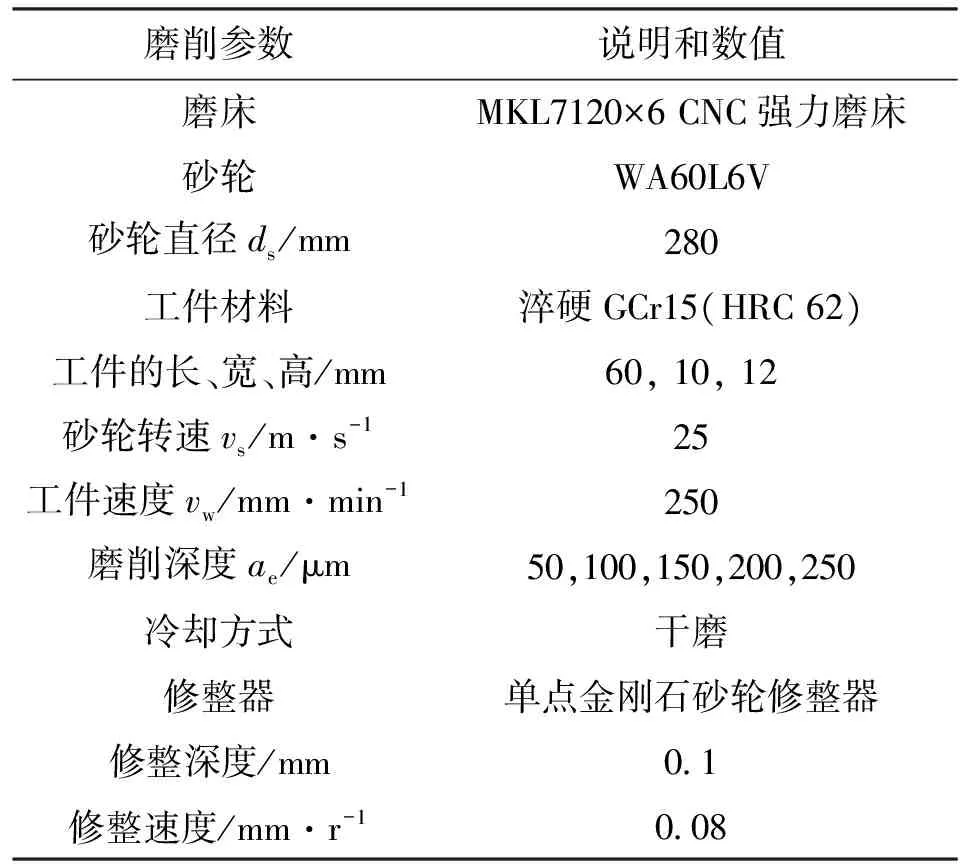
表2 磨削工艺条件
根据表3中的第1、3、5组磨削工艺参数,将求得的形函数s(ω)绘于图6。利用求得的qw与s(ω)

表3 Ft测量值与qw计算值结果
计算已加工表面热源的热流密度分布qwf(ω),利用数值仿真模型模拟工件的磨削温度场。在表3中第1组磨削工艺参数下,温度场分布的实验测量结果与数值模拟结果见图7,发现两温度场分布虽然略有差异,但是总体上较为相近。

图6 不同磨削条件下的已加工表面热源形函数s(ω)

(a)实验结果

(b)模拟结果图7 温度场分布的测量结果与模拟结果

图8 磨削区已加工表面温度分布
在表3中第1组磨削工艺参数下,磨削区已加工表面温度分布的测量与模拟结果见图8,发现两者具有较好的一致性。
在如表3所示的磨削工艺参数下,磨削区已加工表面最高温度的测量与模拟结果见图9。利用测量结果的算术平均值计算相对误差,结果见图9,发现最高温度的模拟值与测量值之间最大相对误差是9.5%,最小相对误差是0.8%。
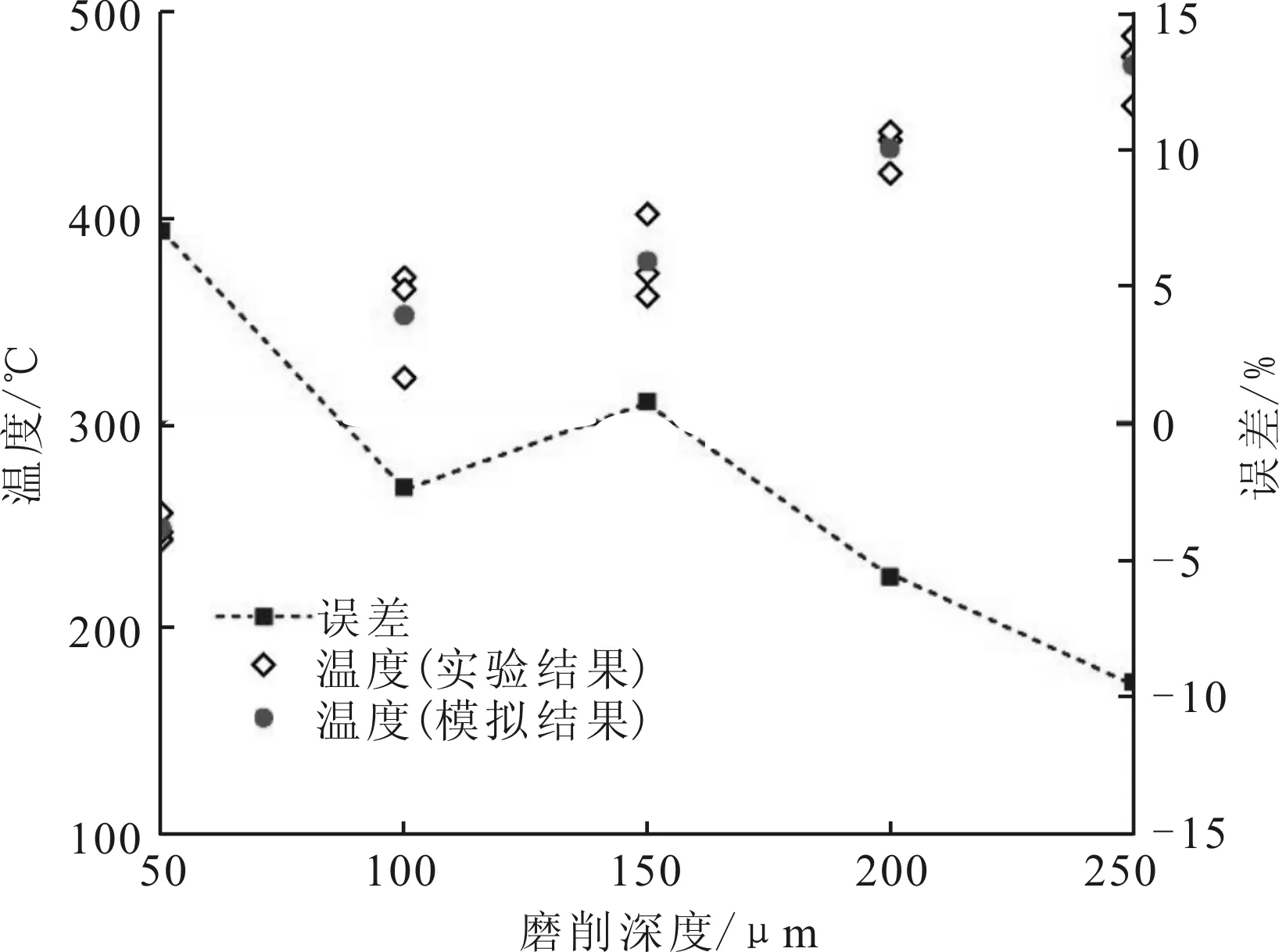
图9 磨削区已加工表面最高温度及相对误差
5 结 论
本文建立了已加工表面热源分布形状的计算方法,利用浅磨模型计算了磨削温度场,结论如下。
(1)已加工表面热源的分布形状随着磨削工艺条件而改变,将已加工表面热源的分布形状假设为某一特定形状,并不适用于所有的磨削工况。
(2)建立的磨削温度场数值仿真模型(浅磨模型)可以准确地模拟工件的磨削温度场,磨削区已加工表面最高温度的模拟值与测量值之间相对误差在0.8%~9.5%之间。
(3)利用浅磨模型对磨削温度场进行数值模拟时,采用本文方法不需预先假设已加工表面热源的分布形状,即可根据具体的磨削条件,获得相应的热源分布形状。
参考文献:
[1]MALKIN S, GUO C. Thermal analysis of grinding [J]. CIRP Annals-Manufacturing Technology, 2007, 56(2): 760-782.
[2]ANDERSON D, WARKENTIN A, BAUER R. Comparison of numerically and analytically predicted contact temperatures in shallow and deep dry grinding with infrared measurements [J]. International Journal of Machine Tools and Manufacture, 2008, 48(3): 320-328.
[3]ANDERSON D, WARKENTIN A, BAUER R. Experimental validation of numerical thermal models for dry grinding [J]. Journal of Materials Processing Technology, 2008, 204(1): 269-278.
[4]MAHDI M, ZHANG L. The finite element thermal analysis of grinding processes by ADINA [J]. Computers & Structures, 1995, 56(2/3): 313-320.
[5]WANG X, YU T, SUN X, et al. Study of 3D grinding temperature field based on finite difference method: considering machining parameters and energy partition [J]. International Journal of Advanced Manufacturing Technology, 2016, 84(5/6/7/8): 915-927.
[6]SHAH S M, NELIAS D, CORET M. Numerical simulation of grinding induced phase transformation and residual stresses in AISI-52100 steel [J]. Finite Elements in Analysis and Design, 2012, 61: 1-11.
[8]ROWE W B, JIN T. Temperatures in high efficiency deep grinding (HEDG) [J]. CIRP Annals-Manufacturing Technology, 2001, 50(1): 205-208.
[9]JAEGER J C. Moving sources of heat and the temperature of sliding contacts [J]. Proceeding of the Royal Society of New South Wales, 1942, 76: 203-224.
[10] GUO C, MALKIN S. Inverse heat transfer analysis of grinding: part 1Methods [J]. Journal of Engineering for Industry, 1996, 118: 137-142.
[11] ROWE W B. Thermal analysis of high efficiency deep grinding [J]. International Journal of Machine Tools and Manufacture, 2001, 41(1): 1-19.
[12] 王德祥, 葛培琪, 毕文波, 等. 磨削弧区热源分布形状研究 [J]. 西安交通大学学报, 2015, 49(8): 116-121.
WANG Dexiang, GE Peiqi, BI Wenbo, et al. Heat source profile in grinding zone [J]. Journal of Xi’an Jiaotong University, 2015, 49(8): 116-121.

