非均匀湍流中螺旋桨激振力宽频谱研究

蒲汲君, 周其斗, 孟庆昌

(海军工程大学舰船工程系, 430033, 武汉)

水下螺旋桨激振力产生的噪声一直以来都受到国内外许多学者的关注和研究[1],该非定常力一般分为两部分:周期力分量和宽频力分量,这些非定常力的产生源于螺旋桨与周围非均匀、非定常流场的相互作用。宽频激振力一般在一阶和二阶叶频处产生较大的波峰,这些波峰的产生主要是由于螺旋桨周围非定常湍流场的影响。为降低螺旋桨激振力产生的噪音,深入研究非定常湍流场中螺旋桨激振力的宽频公式是很有必要的。

已有很多学者都对湍流中螺旋桨激振力进行了研究。Blake使用频谱法研究了螺旋桨激振力的宽频谱公式,但由于在频谱法中对螺旋桨旋转方向的速度相关性进行了过度假设,因此与试验值相比误差较大[2]。Sevik则首次使用了相关性法研究螺旋桨的宽频激振力,但他在研究中只考虑了来流速度对激振力的影响,忽略了螺旋桨旋转带来的影响[3],因此他的研究结果只能显示激振力谱的大致趋势,而不能预报叶频处的激振力波峰现象。随后,Martinez等将螺旋桨的旋转影响考虑在内,成功地在计算中得到了叶频处的激振力波峰现象,但波峰值与试验值相比仍有较大差距[4-8]。Sevik在水洞中研究了10桨叶固定弦长螺旋桨在不同湍流尺寸下的非定常激振力,在试验中显示了激振力宽频谱在叶频处出现波峰的结果,从试验中还发现波峰值随着湍流积分尺度增大而增大的现象[3]。Thompson随后研究了不同桨叶数的螺旋桨激振力宽频谱,他的研究结果显示,随着叶间距离的增大,激振力宽频谱的波峰值随之增大[9]。

在湍流方面,Dryden在试验中对湍流场的基本特性进行了研究,并引入湍流积分尺度Λ来描述湍流速度的相关性规律,他认为推导得到的相关性公式能表达湍流场的基本特性[10]。Taylor等引入湍流特征尺度λ同样对湍流速度的相关性公式进行了研究[11-12],结果表明,在湍流中两点距离相较于湍流积分尺度Λ较小时,使用Taylor等推导的公式是合适的,在距离较大时,Dryden推导的公式则能较好地描述速度的相关性规律[13]。

总的来说,现今对螺旋桨激振力宽频谱的研究还停留在湍流均匀且各向同性的条件下。本文考虑了在螺旋桨前安置导流片的情况(导流片的存在会改变螺旋桨前的湍流特性),并研究了不同叶数的导流片对激振力谱的影响规律。

1　螺旋桨激振力公式推导

1.1　各向同性湍流

相关性法最早由Sevik提出,并与试验值进行了对比,但只能预测推力谱分布的大致趋势[3]。后来,Jiang等在该方法基础上考虑了螺旋桨桨叶的转动,成功地预报了叶频处的波峰现象[5-7]。图1给出了相关性法的原理示意图。下面简要介绍相关性法的原理。单片桨叶在半径r截面处受到的推力为

(1)

图1　湍流导致的激振力示意图

假定湍流场是均匀且各向同性的,于是湍流速度场可由任意两点的速度相关性表示。通过将不同半径处的升力相关性做空间上的积分运算,再取傅里叶变换后可以得到螺旋桨推力谱的表达式如下

(2)

将式(1)代入式(2),得到推力谱的表达式如下

φF(ω)=π2ρ2∬drdr′cosγcosγ′C(r)C(r′)·

(3)

现在问题集中在确定任意两点垂直于桨叶表面湍流速度分量的相关性函数QNN上。在实际工程中,实时测量各点的相关性函数几乎是不可能的,因为这需要在螺旋桨周围安置大量的探测仪,同时还不能对流场产生影响。于是,在计算中一般使用无螺旋桨下的湍流速度场,该湍流速度场已做过大量实验[10],有较好的理论和数据基础。首先引入固定坐标系,将wN的相关性函数QNN用任意方向湍流速度wi的相关性函数Qij来表示

eiN(r,2πS/N)ejN′(r′,2πS′/N+Ωτ)

wj(r′,2πS′/N+Ωτ)=

eiN(R,2πS/N)ejN′(r′,2πS′/N+Ωτ)·

Qij(r,2πS/N,r′,2πS′/N+Ωτ,τ)

(4)

式中:eiN(r,2πS/N)和ejN′(r′,2πS′/N+Ωτ)为桨叶表面垂直方向的方向余弦。

如前所述,湍流场假定为均匀且各向同性的。在该假设下,任意两点纵向和横向速度的相关函数可用g(η)和f(η)表示,其中η为两点间距离。此时,Qij的表达式如下

(5)

式中:δij为Kronecker算子。假设流体是不可压缩的,于是f(η)与g(η)的关系如下

(6)

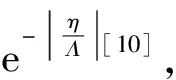
(7)

其中两点间距离分量的表达式如下

ηx=U∞τ

(8)

1.2　各向异性湍流

与各向同性湍流下公式相比,这里主要考虑了桨叶旋转到不同位置时湍流度和来流速度的变化,于是引入时间t

L(r,t,S)=

(9)

与前面均匀湍流下激振力的推导相同,这里假定湍流速度场可由任意两点的速度相关性表示。通过将不同半径处的升力相关性做空间上的积分运算,再取傅里叶变换后可以得到螺旋桨推力谱的表达式如下

∬drdr′cosγcosγ′·

(10)

将式(9)代入式(10),得到推力谱的表达式如下

φF(ω)=π2ρ2∬drdr′cosγcosγ′U(r,t,S)U(r′,t+
τ,S′)wi(r,2πS/N+Ωt,t)wj(r′,2πS′/N+

Ω(t+τ),t+τ)eiN(r,2πS/N+Ωt)ejN′(r′,2πS′/N+

(11)

式中:t为绝对时间;τ为两点间的相对时间。首先设定

wj(r′,2πS′/N+Ω(t+τ),t+τ)·

ejN′(r′,2πS′/N+Ω(t+τ))·

U(r,t,S)U(r′,t+τ,S′)·

eiN(r,2πS/N+Ωt)dt

(12)

这里f(r,r′,S,S′,τ)为包含时间t和τ的所有相关项,详见附录A。

图2　4叶导流片产生湍流示意图

本文计算的是导流片后的螺旋桨激振力,以4叶导流片为例,4叶导流片安装在螺旋桨正前方,距离螺旋桨盘面一倍螺旋桨直径。图2给出了4叶导流片后湍流的示意图。由图可见,在导流片后会产生大量的旋涡,使得相关区域湍流度明显激增,这些不同尺度的涡则是产生宽频激振力的主要原因,而在其他位置来流速度的湍流度较小,螺旋桨盘面处的湍流实际上是非均匀的。这里可以将螺旋桨盘面分为8个区域,从图2中观察可知只有ACEG区域的湍流度较大,所以只有流经这些区域的桨叶叶片才能产生激振力。另外,值得注意的是,ACEG区域中任一区域与其他区域之间都相隔一个湍流度几乎为0的区域(BDFH),所以若桨叶元位于ACEG中不同的两个区域,则它们之间湍流速度的相关性依然为0;只有两桨叶元同时位于ACEG中的任一相同区域时,它们的湍流速度才存在相关性。由于这里主要探究非均匀流场对螺旋桨宽频激振力的影响规律,所以划分的湍流区域只要保证理论推导与实际情况近似相同即可。为简便计算,将湍流区域划分为角度为20°的扇形,以后在试验中可以精确测量各种条件下的湍流场。关于湍流场的数学模型见附录B。

文献[14]指出,在来流靠近螺旋桨盘面时,湍流涡会拉伸变形。图3显示了由于螺旋桨抽吸作用导致的湍流涡拉伸变形的原理。从图中可以看到,在靠近螺旋桨的过程中,湍流涡沿纵向被拉伸变形,导致了纵向湍流积分长度Λx变大,横向湍流积分长度Λy、Λz变小,从而减小了x方向湍流速度的相关性,增大了y、z方向湍流速度的相关性。为考虑湍流涡变形的影响,引入拉伸系数ax、ay、az[6],得到如下关系式

(13)

值得注意的是,湍流涡变形程度与湍流涡的尺寸有很大关系。一般来说,湍流涡的尺寸越大,湍流涡的变形程度越大,因此ax越小,ay、az越大。

图3　湍流涡拉伸变形图

2　计算和对比

2.1　各向同性湍流下计算结果

Sevik在直径为1.22 m的水洞中对螺旋桨在湍流中的非定常激振力进行了研究[3],试验螺旋桨有10片桨叶,无侧斜,桨叶弦长恒定且为25.42 mm,桨叶半径为10.16 cm,桨毂半径为2.5 cm,具体几何形状如图4所示。用于产生湍流的网格有两种尺寸,分别为10.16 cm和15.25 cm,螺旋桨安装的位置分别为网格后24.3 m(20倍网格尺寸)和36.6 m(20倍网格尺寸)。由Dryden的研究结果可知,该种工况下产生的湍流度相同且都为3%,湍流积分尺度为0.2倍网格尺寸。来流速度都保持为4.57 m/s,螺旋桨进速为1.22。

图5和图6分别给出了两种湍流尺度下不同方法计算得到的螺旋桨激振力宽频谱与试验值的比较结果,其中计算参数的取值如表1所示。

表1　计算参数的取值

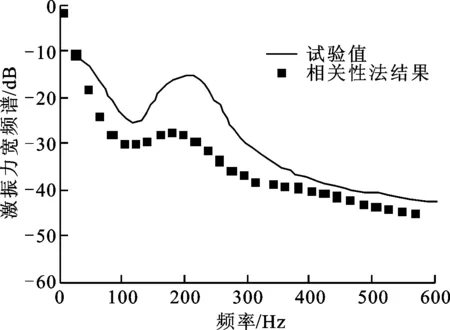
观察图5a可以发现,相关性法的计算结果在一阶叶频处出现较小波峰,该现象与试验结果相同,但波峰值与试验值相比差距较大,在一阶叶频后,激振力宽频谱随着频率的增大而减小,总的来说,相关性法结果的趋势与试验值相比大致一致,但计算值小于试验值,波峰处的误差尤其大。图6a的结果显示,随着湍流积分尺度增大,相关性法的计算结果几乎无明显改变,而试验值在二阶叶频和三阶叶频处都出现了较为明显的波峰,这在计算结果中几乎没有得到体现。由此可以发现,相关性法的计算结果在大致趋势上能与试验值保持一致,但无法准确地预报叶频处的波峰现象。

观察图5b和图6b可以发现,改进后相关性法的计算结果与试验结果的趋势相同,且在叶频波峰处能较好地符合试验结果。特别是在15.24 cm网格下,改进后的相关性法能较好反映二阶和三阶叶频处的波峰现象,虽然二阶叶频的波峰值与试验值相比误差较大,但取得波峰的频率点位置大致相同。由此可以得出结论:将新的湍流速度相关性公式和拉伸系数ax、ay、az引入相关性法后,计算得到的螺旋桨激振力宽频谱能更好地符合试验结果。

(a)初始公式计算结果

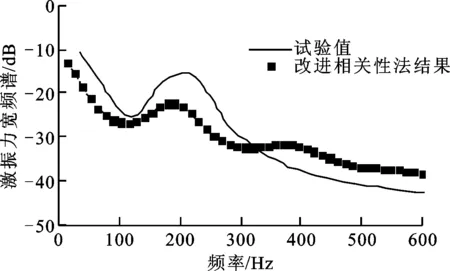
(b)改进后公式计算结果图5　　　　10.16 cm网格下激振力宽频谱计算结果和试验结果[3]

(a)初始公式计算结果

(b)改进后公式计算结果图6　　　　15.24 cm网格下激振力宽频谱计算结果和试验结果[3]

2.2　各向异性湍流下计算结果

在螺旋桨前安置导流片后,螺旋桨盘面的湍流是不均匀且各向异性的,这里分别研究了单叶导流片、两叶导流片和4叶导流片后10叶、5叶和3叶螺旋桨的激振力宽频谱,其中其他参数的设置都与前面各向同性的计算相同,湍流积分尺度Λ=0.02。

图7为10叶螺旋桨在各向异性和同性湍流下的计算结果,可以发现,与各向同性湍流下的螺旋桨激振力宽频谱相比,导流片的存在会大幅度地提高叶频处的波峰,特别是在多阶叶频下激振力宽频谱的波峰现象仍比较明显,与各向同性湍流下的激振力宽频谱有明显区别。这主要是由于在该流场下只有特定区域才能产生激振力,使得激振力的周期性明显增大。另外,较各向同性湍流下的计算结果,加入导流片后螺旋桨激振力宽频谱整体较小。这是由于各向同性湍流下各个区域都有湍流作用在螺旋桨桨叶上,而各向异性湍流下只有导流片后才会产生湍流,随着导流片叶数增加,能产生激振力的区域也随之增大,因此随着导流片叶数增加,螺旋桨激振力宽频谱随之增大。除此之外,还可以发现,各向异性和各向同性湍流下螺旋桨激振力宽频谱取得波峰的位置一致。由此得出,导流片并不会影响激振力宽频谱波峰的位置,该位置依然取决于叶频的大小。

图7　　　　不同叶数导流片下10叶螺旋桨激振力宽频谱计算结果

图8为不同叶数导流片和螺旋桨下激振力宽频谱计算结果,其中10叶、5叶和3叶螺旋桨叶频分别为190、95、57 Hz,观察发现螺旋桨激振力宽频谱波峰的位置都近似位于螺旋桨叶频位置,这也进一步验证了前面的研究。另外,从图中还可以发现,随着螺旋桨叶数增大,激振力宽频谱波峰的幅度也随之增大。由此得出,螺旋桨叶数越多,产生的激振力宽频谱波峰的幅度越大。除此之外还可以发现,在导流片叶数不多(各个导流片产生的湍流都局限在自己的区域,没有发生交汇)的情况下,各个数量导流片下产生的激振力宽频谱在各个频率下的大小相差都相同,激振力宽频谱随频率的变化趋势都基本相同。

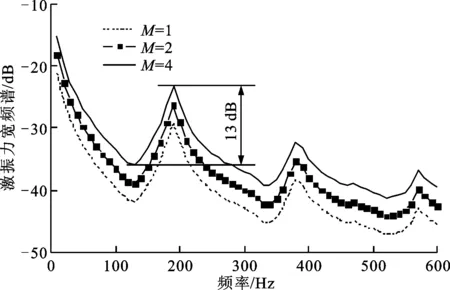
(a)10叶螺旋桨

(b)5叶螺旋桨

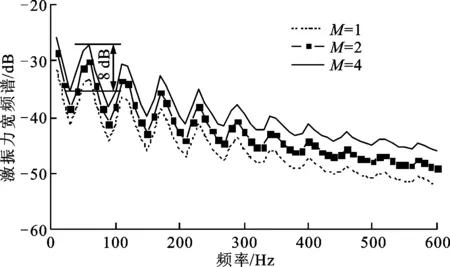
(c)3叶螺旋桨图8　　　　不同叶数导流片和螺旋桨下激振力宽频谱的计算结果

从以上研究可以得出结论,流场的均匀性、各向同性或各向异性并不会对激振力宽频谱的波峰位置产生影响,它们只能影响激振力宽频谱叶频处的波峰程度,一般来说,流场的不均匀程度越大,激振力宽频谱叶频处的波峰程度越大。

3　结　论

本文介绍并推导了计算螺旋桨激振力宽频谱的相关性法,在相关性法的基础上,考虑了螺旋桨抽吸作用导致的湍流涡拉伸变形的影响,引入了拉伸系数ax、ay、az,分别推导了在各向同性和各向异性下螺旋桨激振力的宽频公式,虽然本文并没有对导流片产生的各向异性湍流场进行准确测量,只是进行了一定的假设和估计,但该计算对研究各向异性湍流场下螺旋桨宽频激振力的变化规律有一定的指导意义,本文得到了以下结论。

(1)相关性法只能预报螺旋桨激振力宽频谱的大致趋势,无法得到二阶以上的叶频处的波峰现象。

(2)改进后的相关性法不仅能得到螺旋桨激振力宽频谱的大致趋势,还能较好地预报叶频处的波峰现象。

(3)流场均匀性、各向同性或各向异性并不会对激振力宽频谱的波峰位置产生影响,它只能影响激振力宽频谱叶频处的波峰程度。

参考文献:

[1]屈焕成, 张荻, 谢永慧, 等. 汽轮机调节级非定常流动的数值模拟及汽流激振力研究 [J]. 西安交通大学学报, 2011, 45(11): 39-44.

QU Huancheng, ZHANG Di, XIE Yonghui, et al. Numerical simulation of unsteady flow phenomena and excitation force in control stage of steam turbine [J]Journal of Xi’an Jiaotong University, 2011, 45(11): 39-44.

[2]BLAKE W B. Mechanics of flow-induced sound and vibration: IIComplex flow-structure interactions [M]. New York, USA: Academic Press, 1986; 927-931.

[3]SEVIK M. Sound radiation from a subsonic rotor subjected to turbulence: NASA SP-304 Part 11 [R]. Washington, USA: NASA, 1974.

[4]MARTINEZ R, WEISSMAN K. Spatial-domain analysis of the thrust on a propeller cutting through isotropic turbulence: CAA Rept U-1894-358.47 [R][S.l.]: CAA, 1990.

[5]JIANG C W, CHANG M S, LIU Y N. The effect of turbulence ingestion on propeller broadband thrust [R][S.l.]: Taylor Naval Ship Research and Development Center, 1991: 51.

[6]CATLETT M, ANDERSON J, STEWART D. Aeroacoustic response of propellers to sheared turbulent inflow[C/OL]∥18th AIAA/CEAS Aeroacoustics Conference, 4-6 June 2012, Colorado Springs, CO. [2017-06-15]. DOI: 10.2514/6.2012-2137.

[7]ANDERSON J M, CATLETT M, STEWART D O. Modeling rotor unsteady forces and sound due to homogeneous turbulence ingestion [J]AIAA Journal, 2015, 53(1): 81-92.

[8]CHEN Y, WANG L, HUA H X. Longitudinal vibration of marine propeller-shafting system induced by inflow turbulence [J]. Journal of Fluids & Structures, 2017, 68: 264-278.

[9]THOMPSON D E. Propeller time-dependent forces due to nonuniform flow [D]Pennsylvania, USA: The Pennsylvania State University, 1976.

[10] DRYDEN H L, SCHUBAUER G B, MOCK W C J, et al. Measurements of intensity and scale of wind-tunnel turbulence and their relation to the critical Reynolds number of spheres: NACA Rep [R]. [S.l.]: NACA, 1937: 581.

[11] TAYLOR G I. Statistical theory of turbulence [J]. Proc Roy Soc of London: Series A, 1935, 4151(873): 21-478.

[12] VON K T. On the statistical theory of turbulence [J]. Proceedings of the National Academy of Sciences of the United States of America, 1937, 23(2): 98-105.

[13] DRYDEN H L. A review of the statistical theory of turbulence [J]. Quart Appl Math, 1942: 7-42.

[14] MAJUMDAR S J, PEAK N. Noise generation by the interaction between ingested turbulence and a rotating fan [J]. Journal of Fluid Mechanics, 2000, 359: 181-216.

附录A

这里f(r,r′,S,S′,τ)为包含时间t和τ的所有相关项,继续简化得到

f(r,r′,S,S′,τ)=

E(g(r,t,S)g(r′,t+τ,S′)wN(r,2πS/N+

Ωt,t)wN(r′,2πS′/N+Ω(t+τ),t+τ))

式中:g(r,t,S)为关于来流速度U(r,t,S)的函数,其表达式如下

(A1)

由于湍流函数w(r,2πS/N,t)与来流速度的相关函数g(r,t,S)之间的相关性几乎为0,于是可近似认为

f(r,r′,S,S′,τ)≈E(g(r,t,S)g(r′,t+τ,S′))·
E(wN(r,2πS/N+Ωt,t)·
wN(r′,2πS′/N+Ω(t+τ),t+τ))

(A2)

式中:E为期望函数。将湍流速度和来流速度分别求期望,得到

(A3)

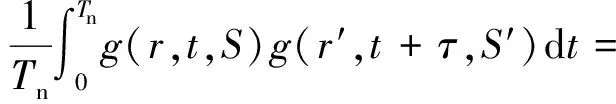
(A4)

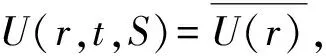
E(g(r,t,S)g(r′,t+τ,S′))≈

(A5)

附录B

按照上文对湍流速度的分析,相关函数有如下定义。

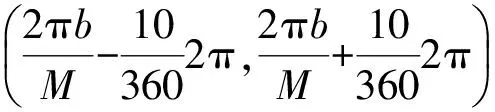
Qij(r,r′,S,S′,τ,t)=

Qij(r,2πS/N,r′,2πS′/N+Ωτ,τ)

此外,Qij(r,r′,S,S′,τ,t)=0,其中b=1,2,…,M,M为导流片总叶数。

[本刊相关文献链接]

陈尧兴,李志刚,李军.非均匀进汽时迷宫密封汽流激振动力特性的研究.2017,51(9):145-152.[doi:10.7652/xjtuxb2017 09021]

李震,琚亚平,张楚华.高精度中心-WENO混合格式在可压缩各向同性湍流大涡模拟中的应用.2017,51(1):25-30.[doi:10.7652/xjtuxb201701005]

李典,刘小民,杨罗娜.仿鸮翼的三维仿生翼型叶片气动特性研究.2016,50(9):111-118.[doi:10.7652/xjtuxb201609018]

任芸,吴登昊,牟介刚,等.考虑旋转和曲率的湍流模型修正及应用.2016,50(9):25-30.[doi:10.7652/xjtuxb201609004]

兰艾青,王志恒,于洪石,等.合成射流激励位置对控制翼型大攻角分离流动影响的数值研究.2016,50(7):110-117.[doi:10.7652/xjtuxb201607017]

李志刚,李军,丰镇平.进口防旋板对孔型密封非定常气流激振特性的影响.2016,50(1):16-21.[doi:10.7652/xjtuxb 201601003]