混合测量子空间聚类算法的研究

金利英, 赵升吨

(西安交通大学机械工程学院, 710049, 西安)

子空间聚类算法是模式识别和数据挖掘等应用领域的重要工具,随着新技术的高速发展,应用环境不断变化,大规模数据与复杂结构数据对子空间聚类算法的需求越来越紧迫。迄今为止,已开发出许多聚类算法[1-2],以实现数据聚类的任务,这些算法在如何定义集群以及如何识别集群方面有很大的不同。K-means算法是最经典且应用最广的聚类算法之一[3],但对聚类中心的初始化非常敏感,影响聚类结果和收敛速度。Huang等在K-means算法的基础上提出了权重K-means算法(WK-means)[4],为每个特征分配一个权重,特征权重与特征尺度因子相关[5]。使用闵可夫斯基距离自动计算每个集群的特征权重,以确保这些权重可以看作是特征调节因子。

现有的大多数子空间聚类算法仅使用一个距离函数来评估各个样本之间的距离,该距离函数难以处理具有复杂内部结构的数据集。通过特征之间权重方向旋转特征空间可进一步提高聚类性能,在向量空间模型中[6],余弦相异性比欧式距离更重要。在特征空间(ESCHD)中[7],余弦相异性可提高软子空间聚类的性能。

受iMWK-means和ESCHD算法的启发,本文提出了混合测量子空间聚类算法(iMWK-HD)。该算法将余弦相异性引入到距离函数中,使闵可夫斯基指数与分配特征权重指数相符,构造新的目标函数。使用该目标函数推导迭代过程中更新规则,促进特征空间的扩展、收缩和旋转,iMWK-HD算法可提高聚类精度和聚类结果的稳定性。

1　iMWK-HD算法

1.1　闵可夫斯基距离和智能K-means算法初始化类中心

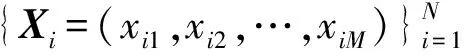
(1)

式中:β为用户定义的参数,表示权重对距离贡献的影响率。d(xi,xj)因β值的不同而变化,指数β≠2不再是特征比例因子。Huang等扩展了相应的闵可夫斯基测量[4],用于测量距离,以确保闵可夫斯基指数与特征权重指数一致。

智能K-means初始化[8](iK-means)是在运行K-means算法之前找出异常集群,即对数据集进行全局加权距离的计算并排序,取最大距离样本点为异常集群,将其设置为初始类中心,在迭代过程中找出距离它最近的样本点,然后从数据集中依次取出;在剩余数据集里取距离最远的样本为初始化类中心,在迭代过程中找出距离它最近的样本点,然后从这个数据集里移出;依次类推,直到剩余数据集为空,之后选取样本点个数最多的异常簇的异常集群为类中心。

1.2　混合测量

基于距离测量准则,在处理高维样本点时会出现维数灾难的情况[9],影响聚类结果的稳定性。将余弦相异性代入优化目标函数中,结合距离计算样本点之间的距离,可促进特征空间转换,样本点xi和第j维k类中心vk之间的距离定义为

(2)

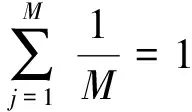
混合测量参数较少、易于实现,可控制数据集在特征空间中的形状、大小和方向,能减小冗余和无关特征对数据集的影响,进而区分特征在不同子空间中的权重大小,提高全局搜索能力。

1.3　目标函数设计

目标函数是评估聚类性能的重要指标,直接影响算法的搜索方向和收敛速度。假设有N个M维数据集X={X1,X2,…,XN},第i个样本点表示为Xi=(xi1,xi2,…,xiM);聚类中心矩阵V={v1,v2,…,vC},C是N个数据集划分类数。利用混合测量求解目标函数最小值,定义为

(3)

式中:矩阵V=[vkj](1≤k≤C,1≤j≤M)为第k类在第j维特征上的类中心值;集群U=[uik](1≤i≤N,1≤k≤C)为第i个样本对第k类的隶属度;矩阵W=[wjk](1≤j≤M,1≤k≤C)为第j维特征对第k类的重要度。

iMWK-HD算法优化目标函数,矩阵U、W的最优解可由下式给出,即

(4)

(5)

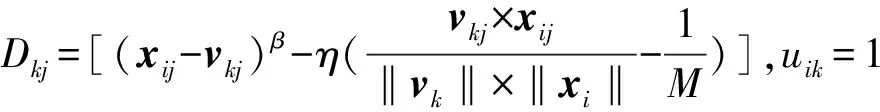
矩阵V的求解可由文献[5]中iMWK-means算法进行迭代更新。式(3)的无约束最小化为

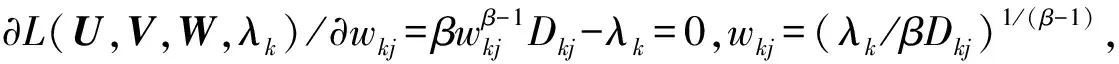
β∈{1.2,2.0,2.3,2.7,3.0,4.9},η∈[0,10],ε=10-5,G=500

iK-means initializeVandWwithwjk=1/M

fort=1:G

UpdataUt+1according to (4) withWtandVt;

UpdataVt+1according toWtandUt+1;

UpdataWt+1according to (5) withUt+1and

Vt+1;

Calculate the objective functionJ(Ut+1,Vt+1,Wt+1) with (3);

if |J(Ut+1,Vt+1,Wt+1)-J(U,V,W)|<εbreak;

End for

OutputWt+1,Vt+1andUt+1。

2　实验设计和结果分析

实验环境为Intel(R) Core(TM) i3-4170 CPU,Windows7,软件开发平台是Matlab 13.0。为验证iMWK-HD算法有效性,与现有的iK-means,iWK-means和iMWK-means算法进行对比。

通过以上对于孟子武德思想的分析与历史经验的侧证，我们可以看到，孟子以“仁者无敌”为核心的武德观，因其精神化理想化的趋向和立意的高标，在国家国际的层面无法得到落实而为荀子所倡的武德原则所取代。而至于共同体与个人的层面，因具有共同追求或现实制度作为基本保障，孟子的武德思想焕发了生命力，具有无穷的魅力。孟子将直接的暴力置换为王霸之辩、天爵人爵之辩、批判精神、大丈夫人格与浩然之气，面对冲突和矛盾，拒绝苟且或残暴而指出向上一路。孟子亦被誉为“中国历史上最有使命感的文化斗士，最有生命力的卫道圣雄”[12](P365)。

2.1　实验数据和评估指标

选取UCI数据库[10]中Wine、Hepatitis、Australian、Liver、Wave、Sonar、Musk这7个数据集来进行对比实验,其基本信息如表1所示。在实验中,使用精确度ACC[11]和RI[12]指标来评估聚类结果的性能,RI定义为

式中:T为在同一类的一对样本点被分到同一类内;E为不在同一类的一对样本点被分到不同的类里;F为不在同一类的一对样本点被分到同一类内;P为在同一类的一对样本点被分到不同类里。ACC、RI取值范围为[0,1],数值越接近1,说明聚类性能越好。

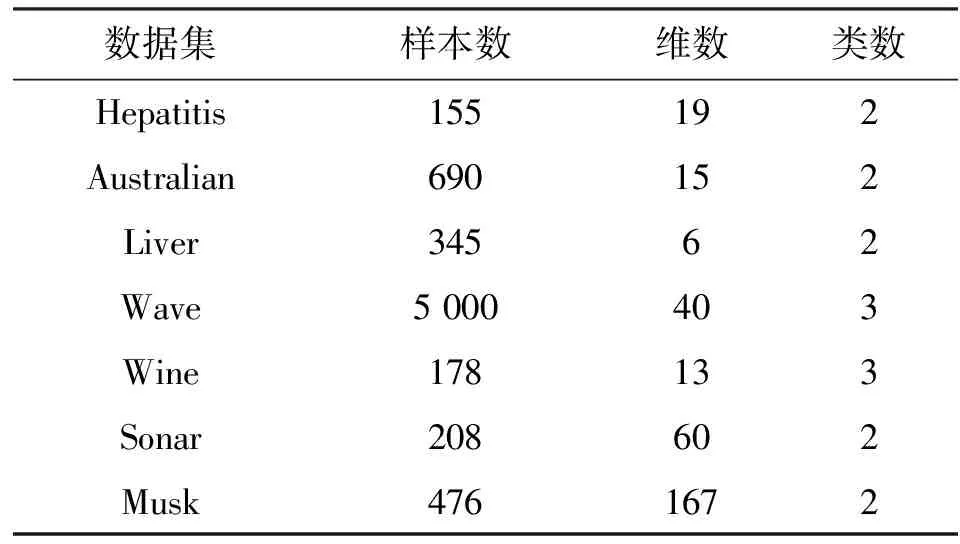
表1　数据描述

2.2　实验结果和分析

算法对7个数据集聚类的最优精度、最优解如表2、表3所示。iMWK-HD算法和iMWK-means算法之间是闵可夫斯基指数β取相同值时对数据集进行实验比较,表中平衡系数η为iMWK-HD算法获得最优实验结果时的取值。

由表2、表3可知:iMWK-HD算法在7个数据集上均获得最优的ACC、RI,高出其他3种算法数个百分点;在聚类结果的稳定性、聚类精确度上,iMWK-HD算法更具优势。这是因为本文将闵可夫斯基距离、余弦相结合构成新的目标函数,使其更好评价特征子集的质量,能更好找到子空间的内部结构,促进样本在特征空间转换,提高全局搜索能力,从而获得更好的聚类结果。

表2　算法对7个数据集聚类的最优精度

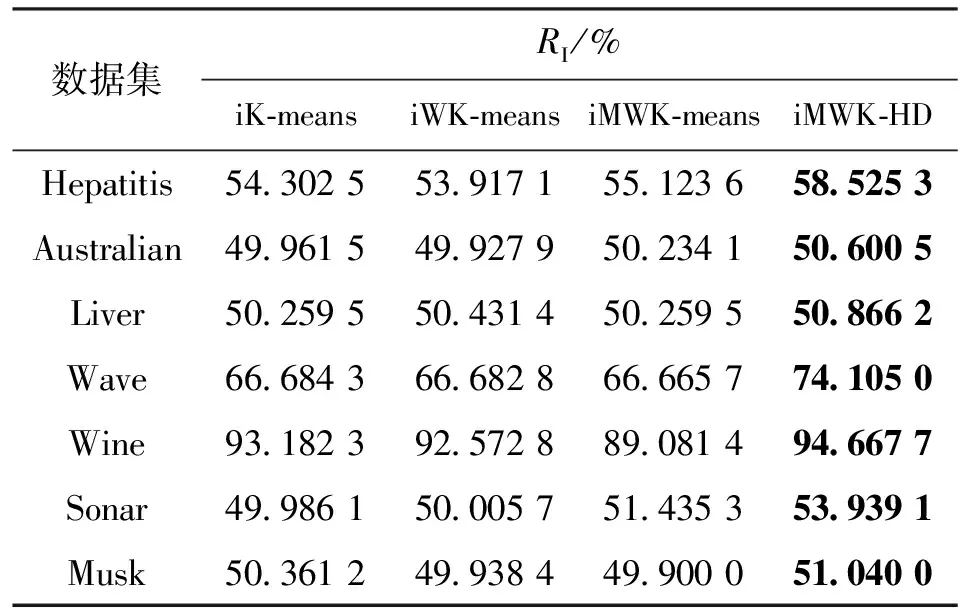
表3　算法对7个数据集聚类的最优解

β、η是iMWK-HD算法的重要参数,对于大规模数据Wave、高维数据Musk,在β取不同值时实验获得的ACC随η的变化趋势如图1、图2所示。

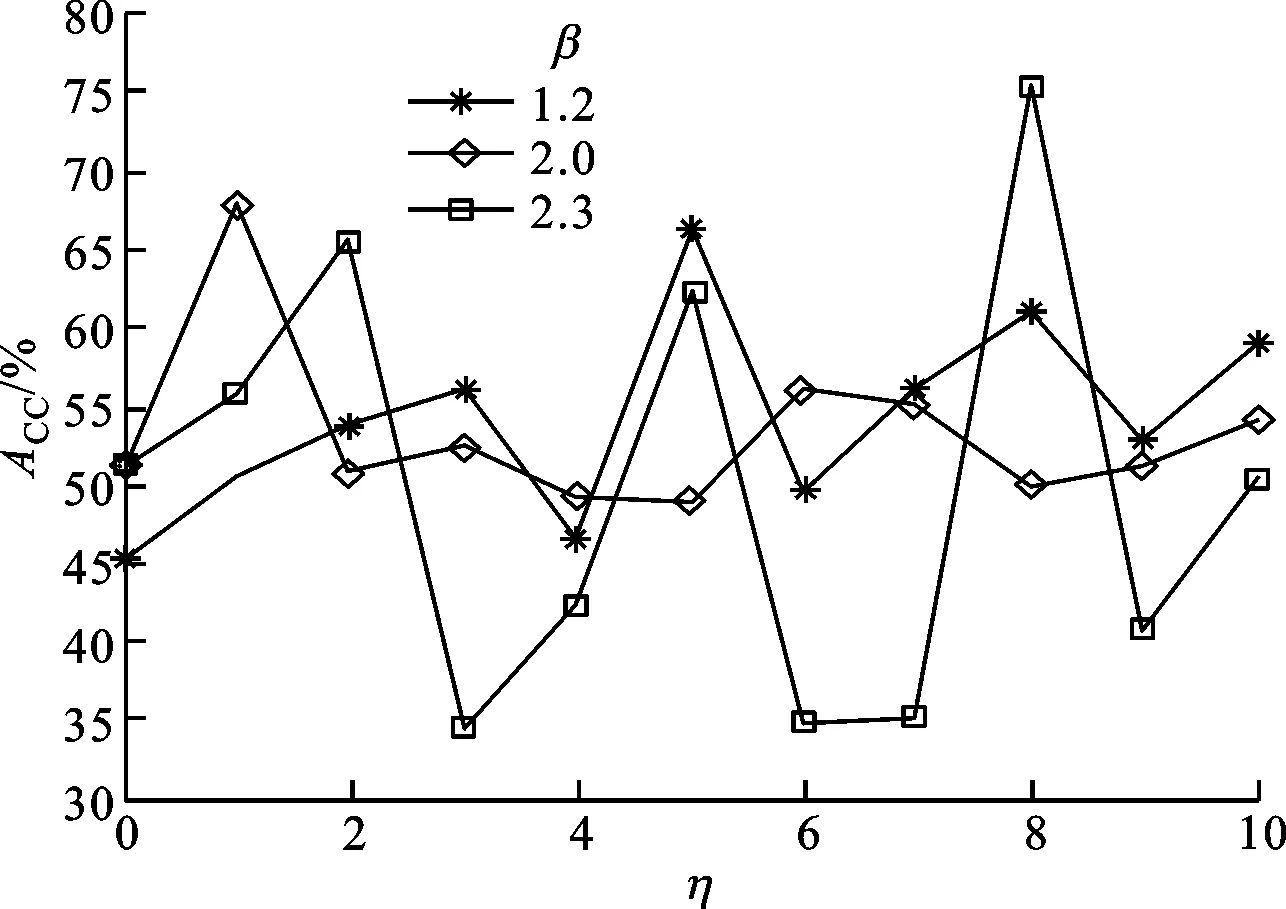
图1　iMWK-HD算法在β=1.2,2.0,2.3时的聚类结果

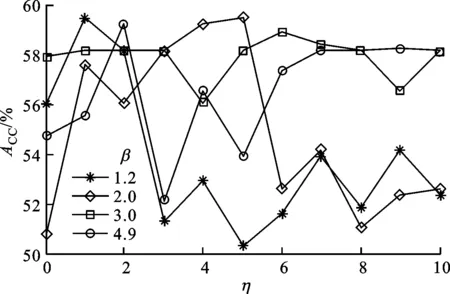
图2　iMWK-HD算法在β=1.2,2.0,3.0,4.9时的聚类结果

由图1中可知,当β=1.2,2.0时,ACC随着平衡系数η的不同取值而变化,且绝大多数ACC优于未引入余弦时的聚类结果,说明引入余弦可增强算法的鲁棒性;当β=2.3且η=3,4,6,7,9,10时,ACC低于η=0时的值,说明对大规模数据而言,β在2.3以内引入余弦能很好地调节特征权重因子,促进特征空间转换,从而提高聚类精确度;当η=0且β分别取1.2、2.0、2.3时,实验获得的ACC分别为45.1%、51.1%、51.3%;当η=1时,ACC分别为50.5%、68%、55.8%;当η=2时,ACC分别为53.7%、50.7%、65.4%;当η取定值时,在β取值范围内,实验获得的ACC与β取值无关,这说明余弦的引入与β不冲突。

由图2中可知,当β=1.2时,ACC随着η的不同取值而变化,且当η=3时,ACC均小于η=0时的值,说明余弦的引入在β=1.2时的聚类结果不稳定。当β=2.0,3.0,4.9时,大部分ACC优于未引入余弦时的聚类结果,对于高维数据,β取值大于2.0时余弦的引入能很好调节特征权重因子,促进特征空间转换,从而提高聚类ACC和算法的鲁棒性。因此,iMWK-HD算法在原子空间聚类算法参数下,有且仅增加一个控制参数η,能最大程度保证算法在高维数据中的聚类精度和聚类结果的稳定性。

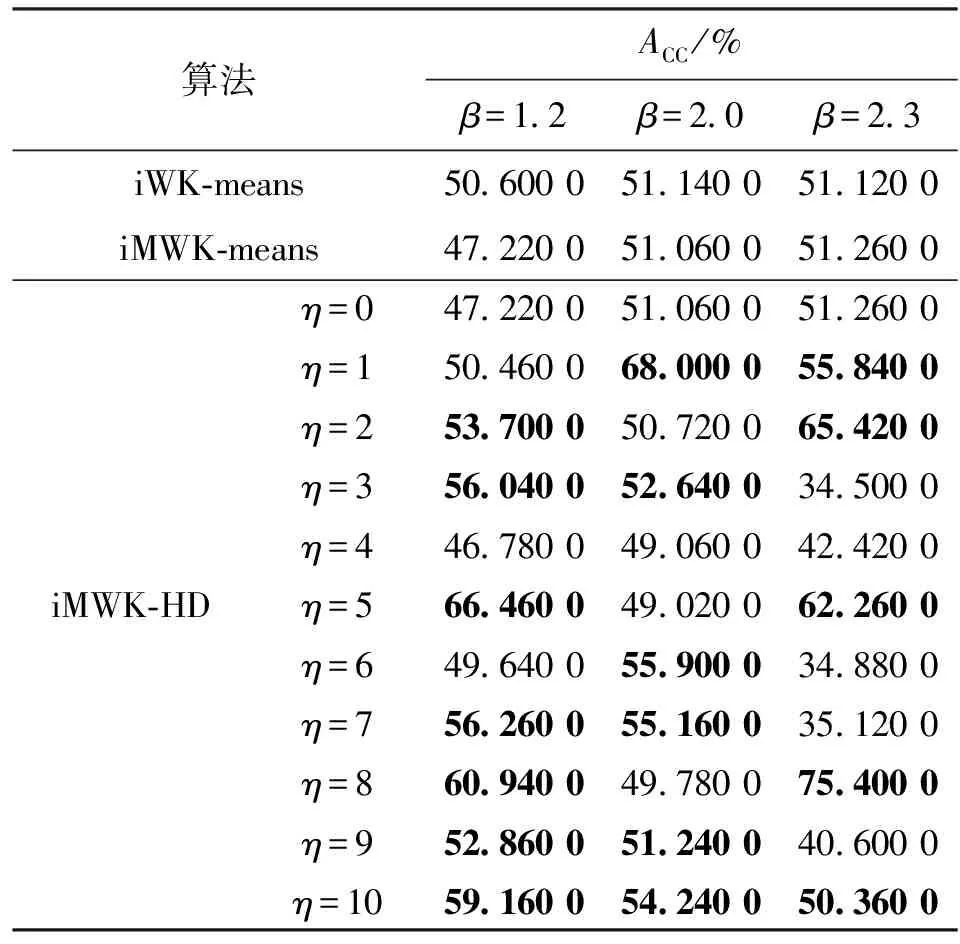
表4　Wave数据集精确度ACC

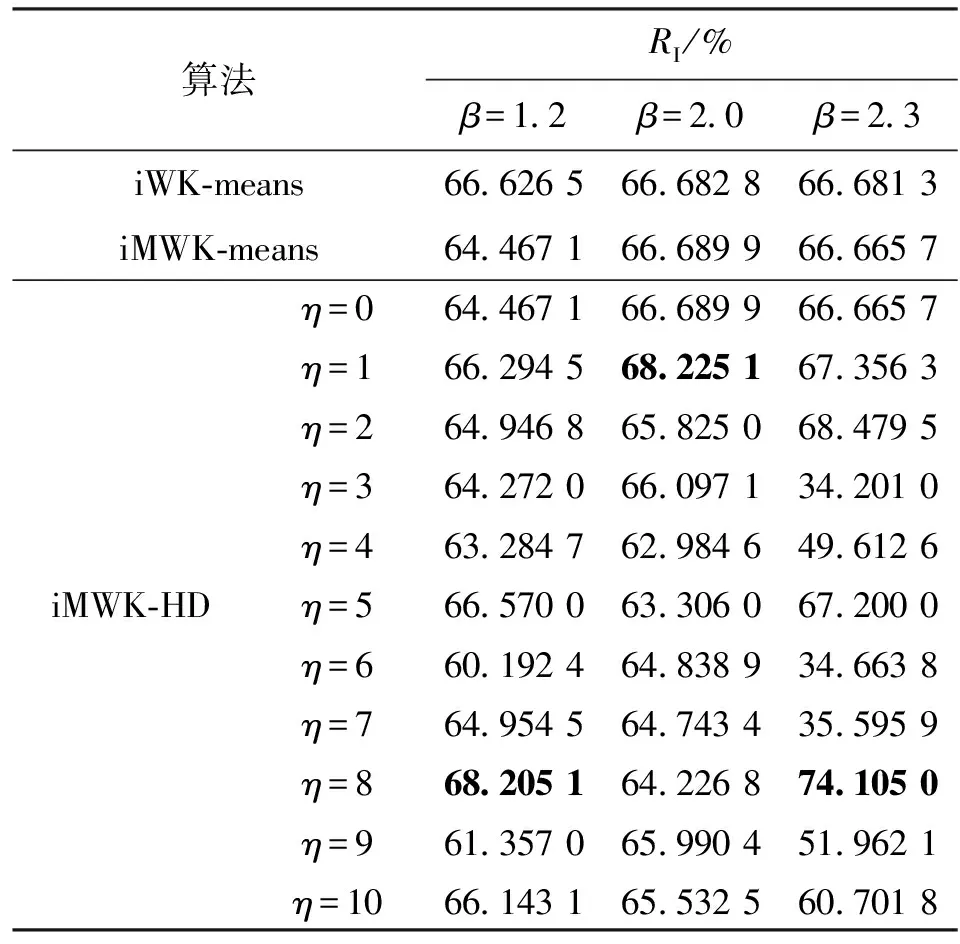
表5　Wave数据集RI

由表4、5可知,当β=1.2,2.0且η=0,即未引入余弦时,iWK-means算法取得ACC最优值,但iMWK-HD算法的ACC与最优结果相差不大,而引入余弦时,iMWK-HD算法的ACC大部分优于iWK-means和iMWK-means算法。当β=2.3且η=0时,iMWK-HD和iMWK-means算法的ACC相同;而引入余弦时,iMWK-HD算法的最优值高出iWK-means和iMWK-means算法分别为24.24%、24.1%,说明iMWK-HD算法具有较强鲁棒性和较高聚类精度。ACC所示的最佳聚类性能并不总是与RI表示一致,因此有必要对不同指标聚类算法的性能进行评估。

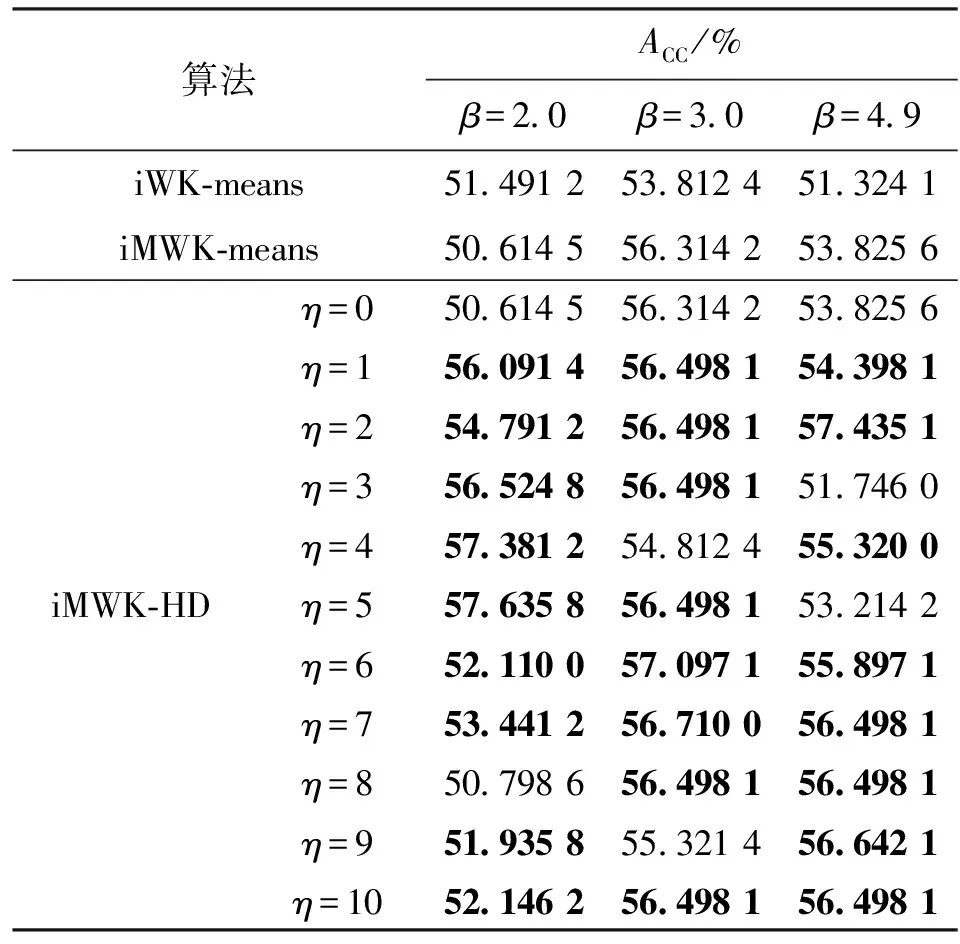
表6　Msuk数据集精确度ACC

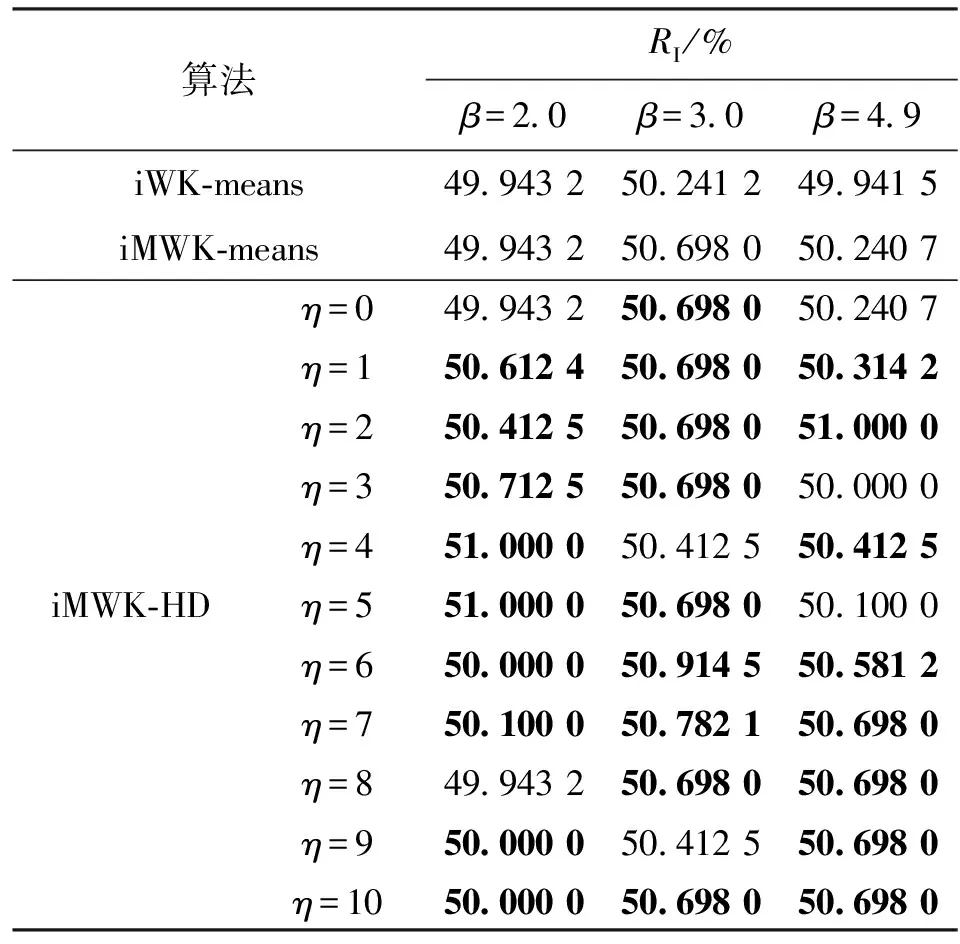
表7　Msuk数据集RI

由表6可知,当η=0,即未引入余弦时,iMWK-HD和iMWK-means算法在β取不同值时ACC、RI均相同;当引入余弦时,iMWK-HD算法在大多数情况下的实验结果均优于iMWK-means和iWK-means算法,只有少数实验结果低于它们,且实验结果相差不大,说明本文所提iMWK-HD算法具有较强鲁棒性。Musk数据虽拥有较高维数,iMWK-HD算法也能有效地提取对应维数信息,再一次体现出iMWK-HD算法的聚类结果稳定性好、聚类精度高的优点。

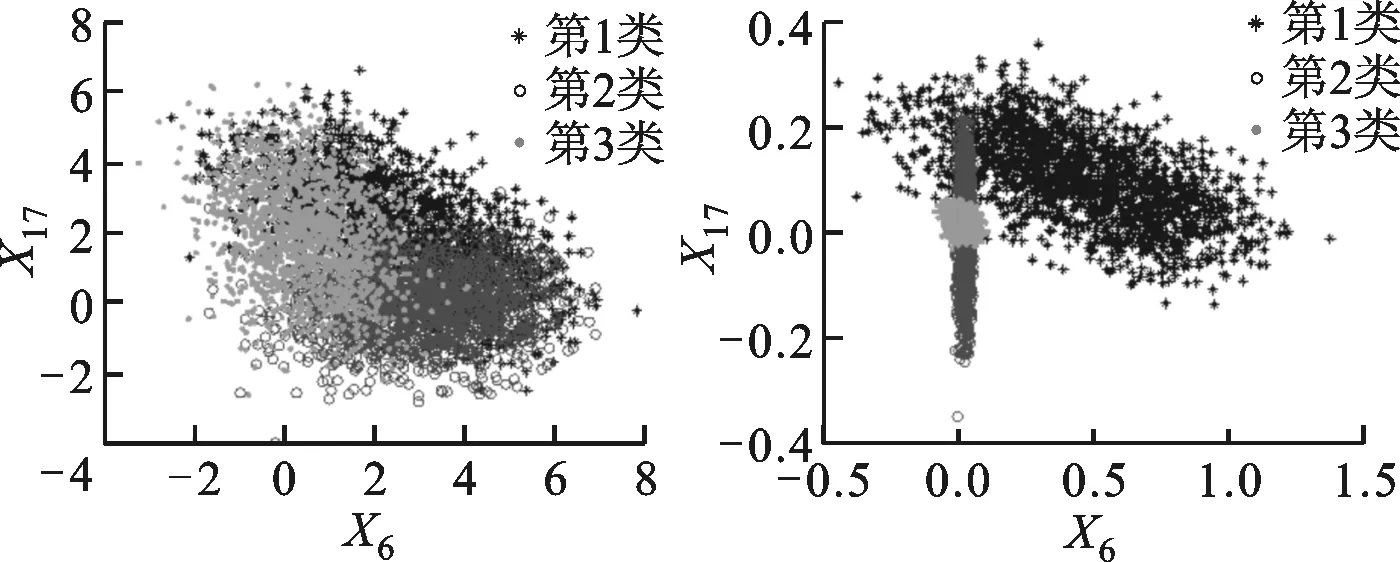
(a)原始数据分配　　　(b)iMWK-HD算法

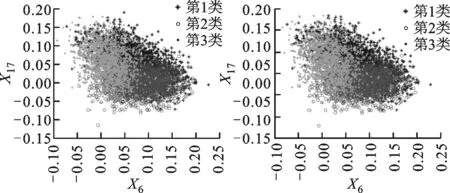
(c)iMWK-means算法　　(d)iWK-means算法图3　　　　Wave数据集中3种算法根据特征权重进行转换的数据分布情况

3种算法根据特征权重进行转换的数据分布情况如图3、图4所示。由图3、图4可知,集群之间的重叠较少,在总体性能上优于另外两种算法,说明iMWK-HD算法聚类结果的稳定性好。这是因为iMWK-HD算法的目标函数中引入了余弦相异性,使特征权重在特征空间不仅能扩展、收缩,还能旋转,iMWK-HD算法能有效提高解的质量。

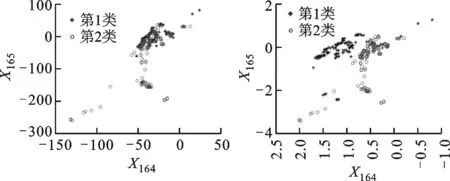
(a)原始数据分配　　　(b)iMWK-HD算法

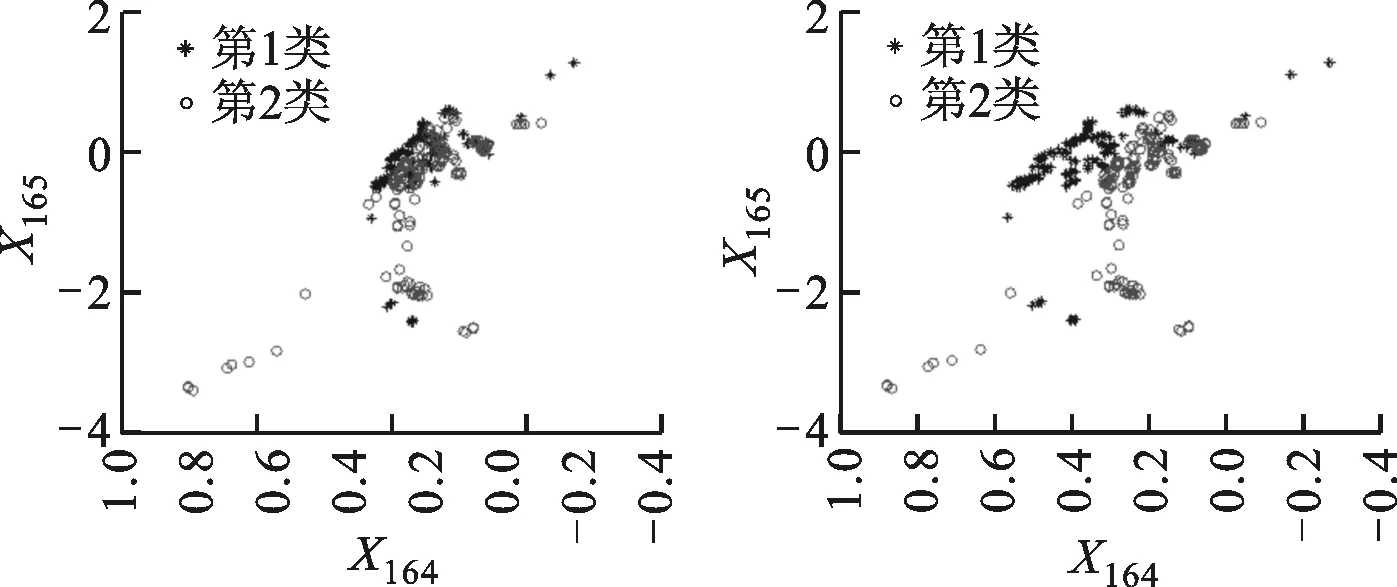
(c)iMWK-means算法　　(d)iWK-means算法图4　Musk数据集中数据分布情况

对比实验结果说明了本文所提iMWK-HD算法的鲁棒性及聚类结果的稳定性。子空间聚类算法能更好发现子空间的内部结构,展现良好的聚类结果。对于Wine数据,各个子空间聚类算法的内部结构如表8所示,将其各维标上对应编号。由表8中前6位特征重要性排序可知,所得各个数据簇的特征排列顺序在每个子空间聚类算法中有所不同,也可在其他数据集中得到类似发现,这种发现子空间的能力可提高聚类有效性。

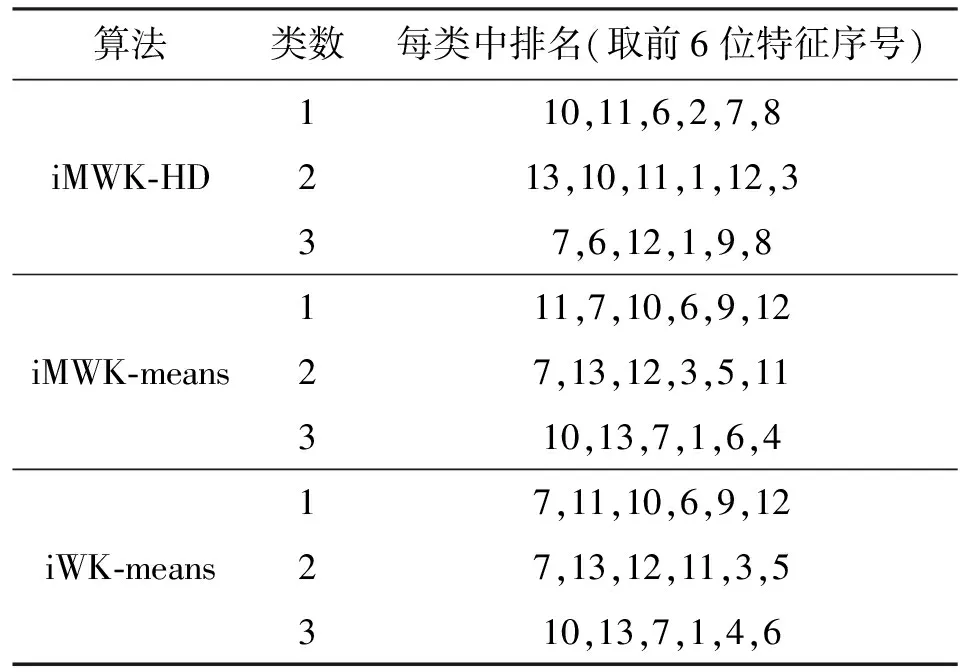
表8　Wine数据集上的特征重要性排序

综上对比实验结果,分析iMWK-HD算法最优的原因:①初始化阶段使用智能K-means算法求解聚类中心点,解决了随机选取类中心导致若干聚类合并及正确选择类数的问题;②混合测量导出样本与中心点的距离,解决了特征空间旋转问题;③利用拉格朗日乘子求解新的隶属度和特征权重迭代更新公式,保证了类中心的稳定性,从而促进特征空间转换,获取有效的聚类结果。实验结果验证了iMWK-HD算法的优越性。

3　结　论

本文提出了一种混合测量子空间聚类算法,该算法是在iMWK-means框架下,将余弦相异性引入到子空间聚类的目标函数中,与闵氏距离相结合,构造了新的目标函数,该目标函数控制参数少,易于实现;利用拉格朗日乘子求解样本点新的隶属度和特征权重迭代更新距阵,实现特征权重因子自动调节,促进特征空间转换,从而有利于隶属度矩阵U的划分和类中心矩阵V的精准度,最终获取样本点的最优聚类结果,提高聚类性能。实验结果表明,与iK-means、iWK-means和iMWK-means三种算法相比,iMWK-HD算法聚类结果稳定性好,聚类精确度高。

参考文献:

[1]PAN Y, WANG J, DENG Z. Alternative soft subspace clustering algorithm [J]. Journal of Information & Computational Science, 2013, 10: 3615-3624.

[2]CHEN X, YE Y, XU X, et al. A feature group weighting method for subspace clustering of high-dimensional data [J]. Pattern Recognition, 2012, 45: 434-446.

[3]MACQUEEN J. Some methods for classification and analysis of multivariate observations [J]. Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, 1967, 1: 281-297.

[4]HUANG Z, NG M K, RONG H, et al. Automated variable weighting in k-means type clustering [J]. IEEE Transactions on Pattern Analysis and Machine Learning, 2005, 27(5): 657-668.

[5]RENATO C D, MIRKIN B. Minkowski metric, feature weighting and anomalous cluster initializing in K-Means clustering [J]. Pattern Recognition, 2012, 45: 1061-1075.

[6]KIM D. Group-theoretical vector space model [J]. International Journal of Computer Mathematics, 2015, 92(8): 1536-1550.

[7]WANG L, HAO Z, CAI R, et al. Enhanced soft subspace clustering through hybrid dissimilarity [J]. Journal of Intelligent & Fuzzy Systems, 2015, 29: 1395-1405.

[8]CHIANG M M, MIRKIN B. Intelligent choice of the number of clusters in k-means clustering: an experimental study with different cluster spreads [J]. Journal of Classification, 2010, 27(1): 1-38.

[9]PARSONS L, HAQUE E, LIU H. Subspace clustering for high dimensional data: a review [J]. ACM Sigkdd Explorations Newsletter, 2004, 6(1): 90-105.

[10] DENG Z, CHOI K S, CHUNG F L, et al. Enhanced soft subspace clustering integrating within-cluster and between-cluster information [J]. Pattern Recognition, 2010, 43(3): 767-781.

[11] HUANG J Z, XU J, NG M, et al. Weighting method for feature selection in k-means [J]. Computational Methods of Feature Selection, Chapman & Hall/CRC, 2007, 193-209.

[12] RAND W M. Objective criteria for the evaluation of clustering methods [J]. Journal of the American Statistical Association, 1971, 66: 846-850.

[本刊相关文献链接]

兰进,徐亮,马永浩,等.实验研究类螺纹孔旋流冲击射流的冷却特性.2018,52(1):8-13.[doi:10.7652/xjtuxb201801 002]

韩树楠,张旻,李歆昊.高容错(2,1,m)卷积码快速盲识别方法.2017,51(12):28-34.[doi:10.7652/xjtuxb201712005]

姜洪权,王岗,高建民,等.一种适用于高维非线性特征数据的聚类算法及应用.2017,51(12):49-55.[doi:10.7652/xjtuxb201712008]

曹岩,韦婉钰,乔虎,等.采用设计结构矩阵的突发事件扩散预测及建模方法.2017,51(12):68-75.[doi:10.7652/xjtuxb 201712011]

王瑞琴,高炎,晏鑫,等.燃气透平尾缘开缝区冷却性能的非定常研究.2017,51(12):98-103.[doi:10.7652/xjtuxb201712 015]

程传奇,郝向阳,李建胜,等.融合改进A*算法和动态窗口法的全局动态路径规划.2017,51(11):137-143.[doi:10.7652/xjtuxb201711019]

黄兴旺,曾学文,郭志川,等.采用改进二进制蝙蝠算法的任务调度算法.2017,51(10):65-70.[doi:10.7652/xjtuxb2017 10011]

舒帆,屈丹,张文林,等.采用长短时记忆网络的低资源语音识别方法.2017,51(10):120-127.[doi:10.7652/xjtuxb2017 10020]

曹卫权,褚衍杰,李显.针对机器学习中残缺数据的近似补全方法.2017,51(10):142-148.[doi:10.7652/xjtuxb201710 023]