基于灰色模型的手机灰色故障率的研究及应用

刘亚晖　林　骏　林　劲　薛晓庆

1(同济大学软件学院　上海 201804)2(迈创智慧供应链股份有限公司　上海 200120)

0　引　言

随着大数据和数据科学技术的兴起，基于数据驱动的方法，研究有效的预测方式，为备件库存的控制和智慧供应链的建设提供了全新的思路。本文基于灰色模型建立灰色故障率公式，并基于故障率曲线中的澡盆曲线原理提取不同手机型号的故障率特征值，进而通过历史机型故障数据来评估新机型完整生命周期中的故障率水平和分布，根据新机型销售计划以预测新机型的故障数量，相应地制定产品投入市场之前的合理备件采购方案。

本文中术语的定义：

手机故障数FC(Fault Count)：是指手机在保修期内，由于手机使用或手机本身的质量问题，导致的手机无法工作或部分功能失效后，手机用户通过保修网络提交并经确认的手机故障的数量。

手机故障发生有相当大的随机性，同时手机销量巨大，使用的人群和环境差别很大，因此其受随机因素的影响较大。另外，手机故障发生与手机报修之间也存在一定的时间关系。比如从数据分析中明显可看到周末(含周六和周日)故障数量极少，接近零，这应该是与周末为休息时间，即使发生故障，一般也是工作日才去报修，这也会带来一些时间上的人为偏差。这类偏差并非随机偏差，属于周期性偏差，可通过按周统计来消除。

手机在保量TC(Total Count)：是指手机销售后仍在保修期内的样本数量。手机销售后都有保修期，一般为15个月，超出保修期后，维修成本较高，同时也面临手机更新换代，很少有用户会去维修，因此，手机故障主要体现在手机保修期内。由于具体销售数据较为敏感无法精确获取，目前通过实际批次发货数据进行销售进度评估并累加计算手机在保量。

手机故障率FR(Fault Rate):是指单位手机数量上发生故障的比例，一般会随着时间变化而变化，相应得到的故障率曲线。手机故障率计算公式为：

FR=FC/TC

(1)

考虑到一般机电设备的故障率曲线都符合U型，即澡盆曲线，见图1。它表示前期设备故障率一般会偏高，随着生产的稳定，故障率会下降并稳定在某个水平上，随着时间的偏移和元器件的老化，设备故障率还会再次变高。手机的生产分为手机试生产、小批量生产和大批量生产，其故障率会在前期试生产和小批量生产时出现一些故障率上的波动，后期大批量生产后，其故障率也会稳定在一个相对固定的水平上。由于手机保修期的原因，超出保修期的手机一般不再维修，即澡盆曲线的末段一般不会达到，手机故障率一般会体现在澡盆的前半段，后续的故障率分析会体现这一特点。

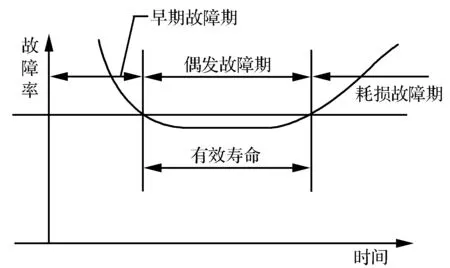
图1　设备故障曲线示意图

1　灰色模型

灰色模型GM(Grey Model)，由于系统被噪声污染，原始数据呈现离乱的情况，离乱的数列称为灰色数列，或者灰色过程，对灰色过程建立的模型，便称为灰色模型[1]。灰色模型是相对于白色模型和黑色模型而言的，白色模型是指系统中所有数据和变量均为明确的模型，黑色模型则指所有数据和变量均不明确的模型。灰色模型则是指数据和变量部分明确的模型，其中就有噪声污染或随机误差导致的灰色模型。灰色模型是大部分系统对应的模型。灰色序列生成是灰色系统的一个基础方法，灰色系统理论认为：原始数据是杂乱无章的，通过数据生成，能得到随机性弱化和规律性强化的生成数列，最常用的是累加生成和累减生成[2]。本文中主要针对手机故障数量进行累加处理。灰色模型的研究中，也有很多论文针对灰色模型进行多种改进以提高灰色模型预测的精度和效果[3-5]。灰色模型的改进主要是针对预测目标的不同特性及原始灰色模型的不足，结合其他预测方法或数学模型进行改进。针对本文中的手机故障，原始的灰色模型体现了非常好的预测效果，结合手机故障问题进行相应的公式推演和转化分析，取得了较好的预测精度。

Wu等[6]针对灰色模型应用的规模进行一些研究。Cui等[7]、Mao等[8]和杨杰等[9]则提出了一些改进的累加方法来提高灰色模型的预测效果。刘思峰等[10]总结了灰色模型近10年的研究综述，列举了灰色模型应用于各种场景及其改进模型。刘思峰等[11]则对最新的灰色系统研究进行了系统总结。本文尝试结合灰色模型和统计数据来进行预测。

下面给出采用灰色模型时所使用的术语：

随机误差也称偶然误差或不定误差，是由于在测定过程中一系列有关因素微小的随机波动而形成的具有相互抵偿性的误差。随机误差的大小和正负都不固定,但多次测量就会发现,绝对值相同的正负随机误差出现的概率大致相等,因此它们之间常能互相抵消。

灰色模型GM与随机误差灰色模型GM中就有专门针对随机误差或称噪声污染的机制，即通过累加原始数列，即可利用随机误差的相互抵偿性，最大程度地减弱随机误差的影响。本文中主要针对原始数列采用累加方式产生新的灰色数列。

考虑N个变量X1,X2,…,Xn，有N个数列：

式中：i=1,2,…,N。

(2)

此时，根据原始数列经过一次累加，可以得到一个新的灰色数列。由于新的灰色数列已通过累加抵消了大部分的随机误差，新数列将更接近真实的数列。

2　手机灰色故障率及手机故障灰色预测

2.1　手机灰色故障率公式

故障率预测一般分为个体预测和整体预测，整体预测中一般包含大量的个体，因此个体带来的随机性会在整体预测上带来非常大的影响。基于灰色模型针对随机误差的抵消作用，本文尝试定义灰色故障数FCgm和灰色样本数TCgm：

(3)

(4)

基于式(1)、式(3)、式(4)，定义了灰色故障率公式：

(5)

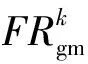
考虑到灰色模型的应用，手机故障率采用累加的故障数量/累加的在保量来得到一个灰色故障率曲线。此时，累加的在保量和累加的故障数量是在同一级别，灰色故障率曲线将接近真实的灰色故障率曲线。

2.2　手机故障数量分布分析

为了验证灰色模型的预测效果，从公司的数据库中选取某品牌销量最大的三个机型的长达3年的历史数据进行相应的数据分析和预测。手机故障数量根据不同机型的时间序列分布，可以画出相应机型的故障散点图，见图2。其中可以看出手机故障数量是在较大范围内宽幅振荡，即随机误差影响较大，同时，也会出现一些明显接近零的故障日期，大部分是周末。

图2　三种机型的故障数量散点图

为了减少随机误差的影响，通过式(3)累加得到灰色模型下的灰色故障数(灰色累加故障数)曲线则要平滑得多，见图3。

图3　三种机型的灰色累加故障数折线图

2.3　手机在保量分布分析

通过计算相应手机型号的在保量，可形成相应的在保量折线图。如图4所示。

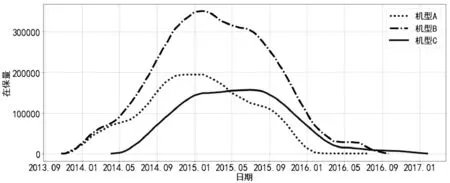
图4　三种机型的在保量折线图

从图4可见，在保量的折线图呈现明显的山峰形状，即开始销售时，在保量开始增加，形成山峰的上坡段，销售完毕部分先期销售的机型退出保修期，开始山峰的下坡段。通过式(4)累加得到灰色模型下的灰色样本数(灰色累加在保量)图形如图5所示。

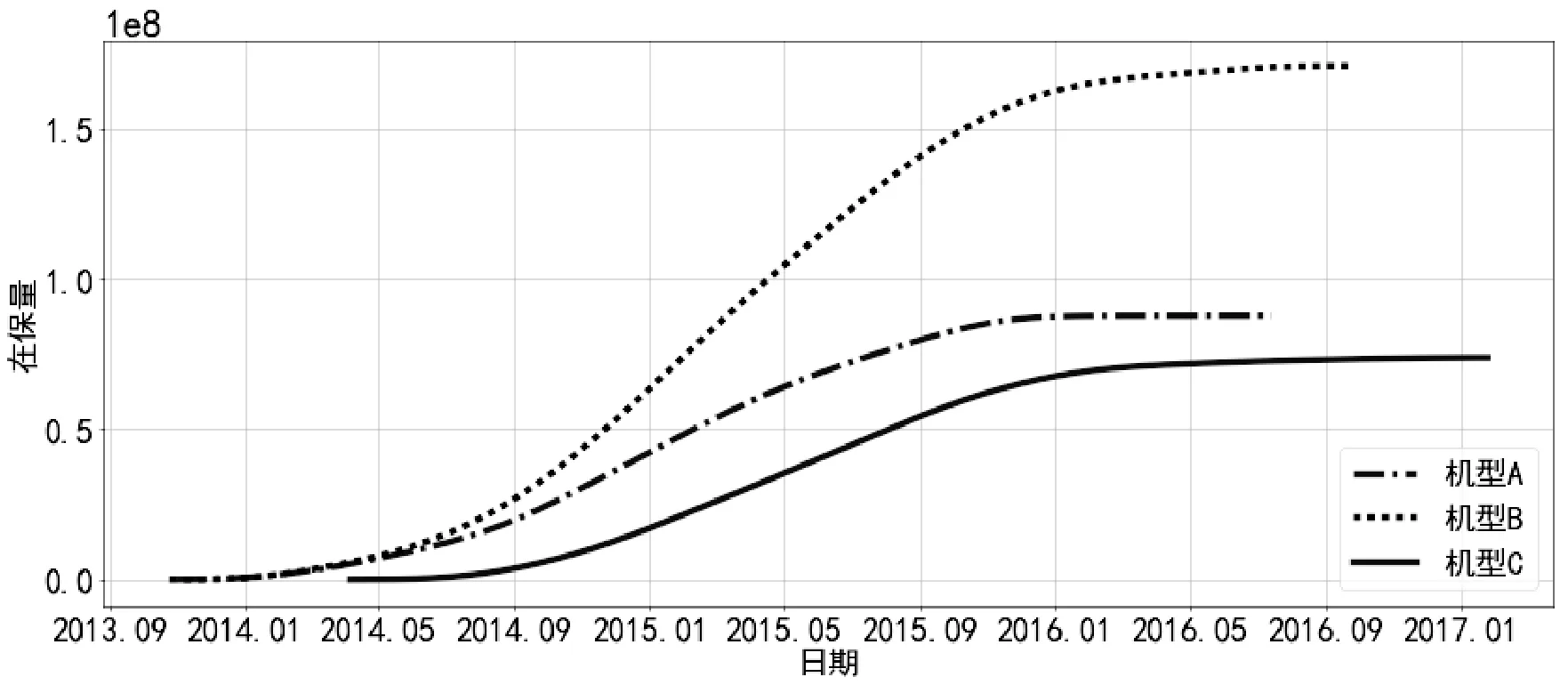
图5　三种机型的灰色累加在保量折线图

2.4　手机故障率分析

根据式(5)将上述三种机型的累加故障数量和在保量累加值相除，得到相应机型的灰色模型下的手机灰色故障率，并画出曲线，如图6所示。

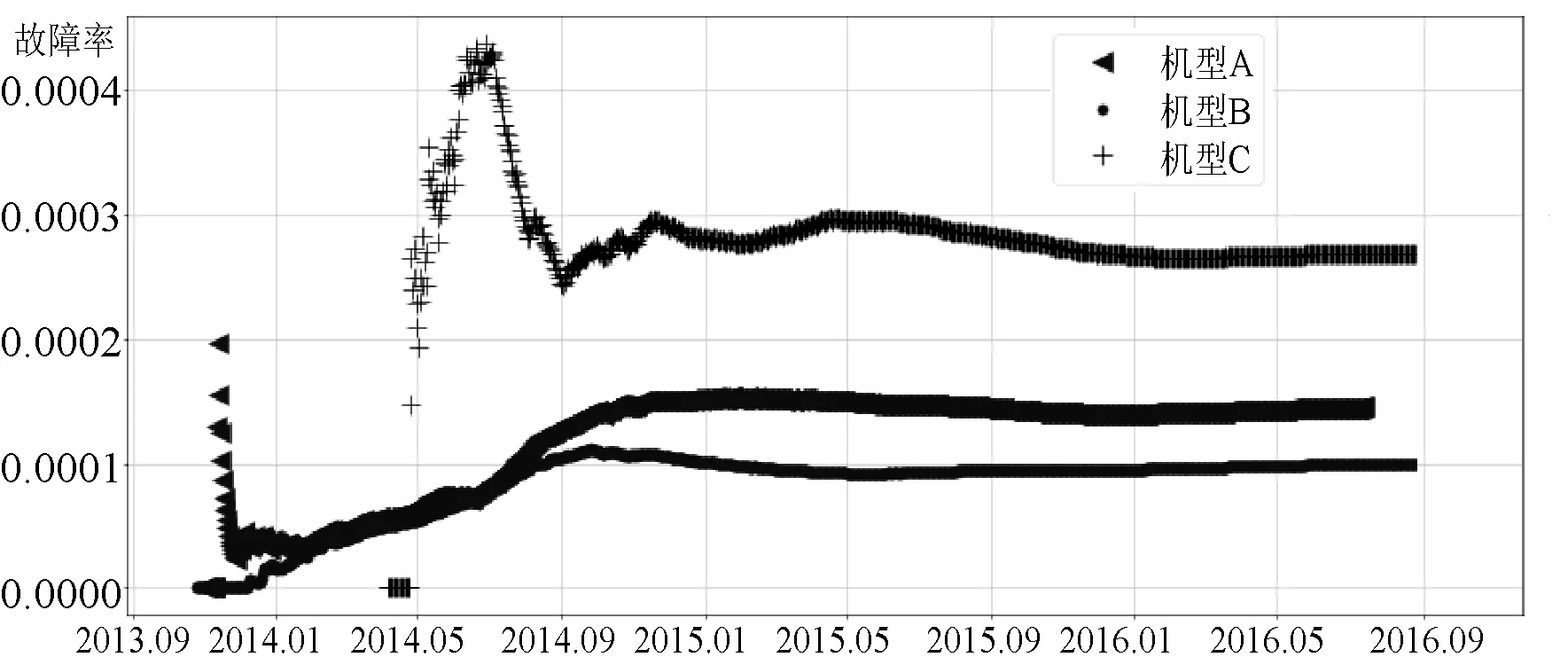
图6　三种机型在灰色模型下的灰色故障率曲线

其中可见三种机型前期有一定波动，后期都稳定在一个波动很小的水平线附近。相应的解释为：随着手机生产厂商手机型号成熟和大批量采购和生产，其批次质量随时间越来越稳定，同时灰色模型的抵消随机误差的作用随时间越来越大，前期累加的数量较小，随机误差作用仍较明显，后期累加数量较大，随机误差抵消充分，故障率能稳定在一个非常平稳的水平线上。因此，此时的故障率可视为该手机型号的实际故障率水平，从逻辑上可以取相应机型最后6个月内的故障率最低值作为该机型的故障率特征值。

2.5　手机故障预测

上述手机故障率分析，能得到历史机型的故障率分析结果及相应的故障率特征值。

针对新机型的故障率特征值，可通过聚类分析，基于不同机型的厂商、主要部件型号和故障率分析、机型的定位(旗舰机型、中档机型、入门机型等)、机型的功能定位(拍照手机、音乐手机、老人机等)等机型具体信息进行聚类，并选定同一聚类类型中的典型机型的故障率特征值作为新机型的故障率特征值。

定义故障率倍数R，并代入式(5)推导得出：

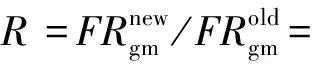
(6)

式中：R为新机型故障率特征值对旧机型故障率特征值的比值；上标new或old分别表示新旧机型的灰色故障率、灰色故障数和灰色样本数。

(7)

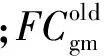
为了验证灰色故障率模型的预测效果，三个机型A、B、C中，选定机型A作为标准机型，即用于预测的新机型，机型B和C作为参照机型，即已知故障完整信息的历史手机。在已知机型A的故障率特征值的基础上，利用参照机型B和C的故障率特征值，进行相应机型A的故障预测，实际和预测出来的数据的时间序列显示在同一张散点图中。如图7所示。

图7　三种机型中实际故障数量与预测故障的散点图

从图7中所示，可以看到相应的故障点的分布体现出较大的随机性，虽然有一些分布上的分散，但三个散点图的整体重合度较高。

为了集中显示预测与实际的故障数，借助灰色模型原理，针对上述故障分布按2周为单位进行累加，得到2周为周期的灰色故障分布，并汇总在图8中。本文也尝试过使用1周和4周作为周期进行统计，其结果与2周的分析非常类似，没有明显不同。图8中可以看到相应的曲线的重合度相对较高，但由于随机性影响，偏差还是较大。

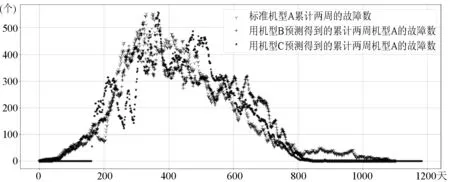
图8　三种机型中2周为单位的实际与预测故障折线图

为此，针对上述数据进行了进一步的数据分析，结果见表1。可以看到以2周为单位的预测时，其平均标准差分别为73和53个，占比分别为28.21%和20.56%；但考虑正负值的平均值，则误差急剧下降为0.60个，占比为0.23%，这也非常符合随机误差能相互抵消的特性；另一机型的预测分析结果类似，总生命周期预测偏差仅为0.19%。

表1　基于机型B和C来预测机型A的预测数据分析

为了更明显地显示灰色预测与实际故障的对比，将标准机型A与参照机型B和C针对标准机型A的灰色预测故障数量进行累加并绘制在图9中。

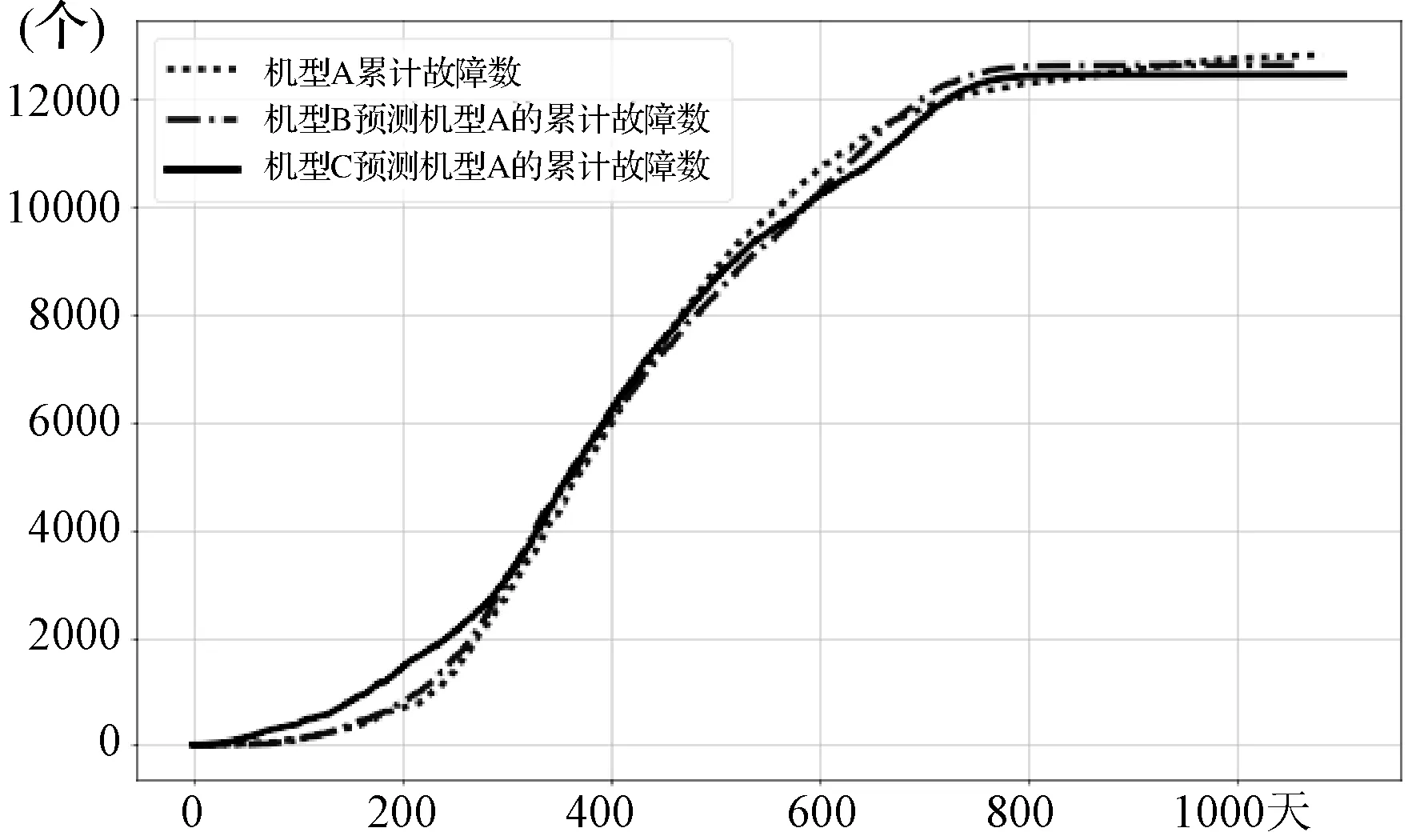
图9　标准机型A与参照机型B、C预测与实际故障数对比图

图9中，机型A的实际累计故障数为12 689个。而参照机型B和C针对机型A的灰色预测的故障数累计值分别为12 723.66和12 433.51，其误差为+0.273%和-2.01%，误差范围非常小。

3　灰色模型预测与移动平均预测的对比

最基本的预测方法是移动平均的预测，也是目前实际预测手机故障率所采用的方法。采用的前4周作为移动平均来进行后4周趋势分析来预测后面的故障率。为了对比，将按预测周期分为1周、2周、4周和6周进行预测，相关图形见图10和图11。随着预测周期的延长，预测值与实际值的偏差也在明显放大，超过6周的预测已经偏差到无法使用。

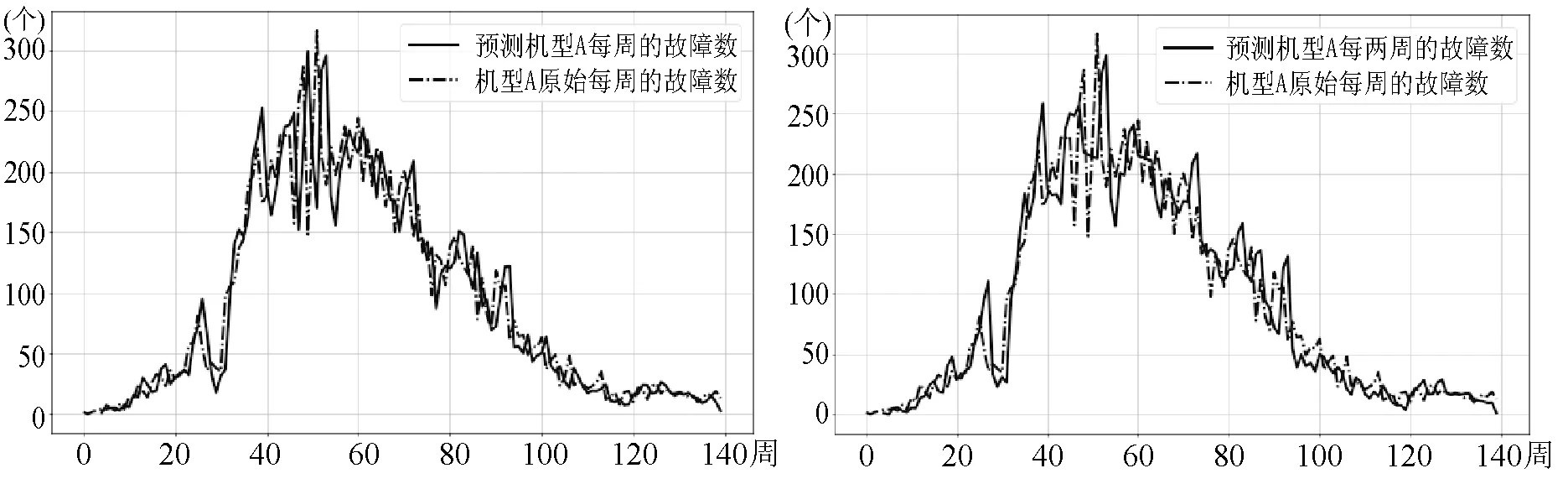
图10　移动平均预测1周(左)和2周(右)的对比

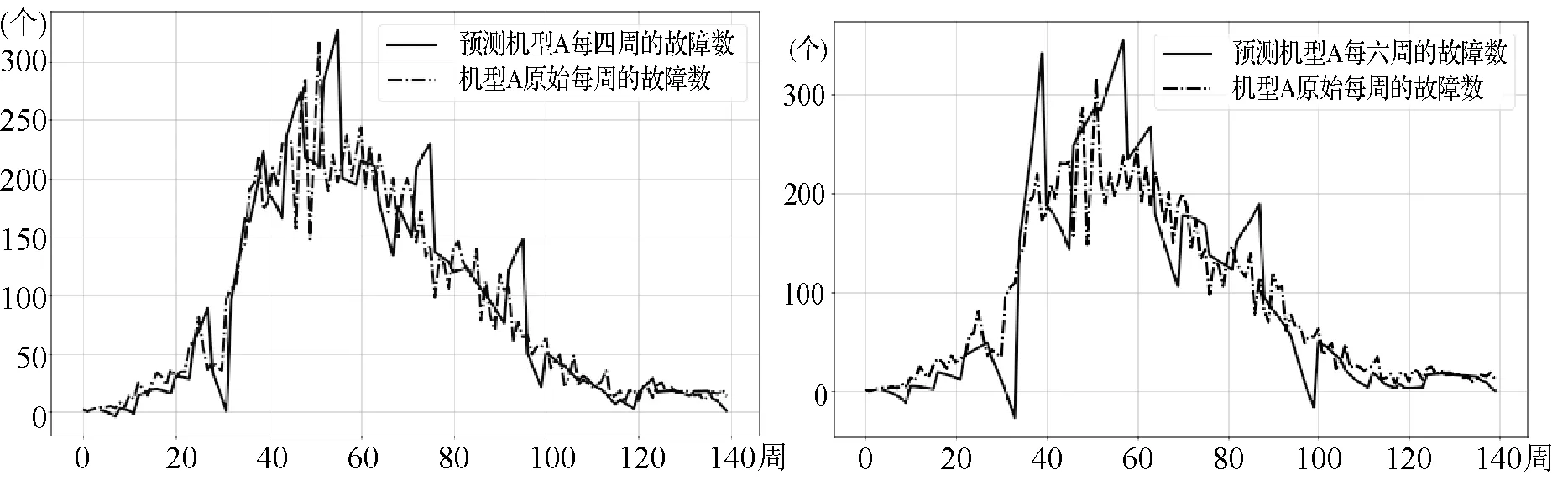
图11　移动平均预测4周(左)和6周(右)的对比图

本文还尝试利用多元多次回归方程针对不同手机型号的故障数据进行回归分析，并对其他机型故障进行拟合预测，由于手机故障随机性较强，拟合效果很不理想。

趋势预测限于其本质特征只适应于短期预测，无法适应全局预测，周期太短预测意义较小，周期太长，偏差太大，预测意义也有限。本文中的灰色故障预测则能针对预计的产品销售进度进行全生命周期的有效准确的预测，有着很高的现实应用价值。

4　结　语

本文基于灰色模型和故障率曲线的研究，建立了灰色故障率定义及公式，通过分析手机故障率曲线特征，提出手机故障率特征值概念。通过新旧机型特征值概念得出新机型故障灰色预测的新方案。新预测方案通过实际手机故障数据予以验证，取得三年全生命周期预测偏差2%左右的精确效果。

以上分析是针对已知机型数据的验证，对于全新的机型，由于没有历史故障信息，其真实的故障率水平仍是未知。但这可以通过机型厂商、机型的主要部件等相似性进行聚类分析，得到全新机型与已知机型的相似程度，从而评估其故障率水平。同时，随着新机型的销售和售后数据的更新，实际发生的故障率数据可对估计故障率进行修正，从而得到更为精确的预测。

本文中的手机故障有着较为特别的属性，包括周期性很弱，数量巨大，随机性很强，预测更侧重为较长周期的准确性，这都为灰色模型的直接应用提供了坚实的基础。有了较为精准的故障预测模型，就可以针对新产品进行故障率水平的评估和故障数量的评估，并进而制定合理的备件采购计划。然后基于最优库存模型，以最经济的批量和采购方式，解决全生命周期的故障备件采购，从而优化手机售后服务的质量和成本。

[1] 邓聚龙. 灰色系统综述[J]. 世界科学, 1983(7):3-7.

[2] 陈勇明. 基于统计视角的灰色系统的几个基本问题的研究[D]. 成都:西南财经大学，2008.

[3] 马良荔，李刚，陶道强．基于灰色GM(1，1)模型的故障预测方法[J]．计算机应用与软件，2013，30(4)：198-200．

[4] 李梦婉, 沙秀艳. 基于GM(1,1)灰色预测模型的改进与应用[J]. 计算机工程与应用, 2016, 52(4):24-30.

[5] 王璐,沙秀艳,薛颖. 改进的GM(1,1)灰色预测模型及其应用[J]. 统计与决策,2016(10):74-77.

[6] Wu L, Liu S, Yao L, et al. The effect of sample size on the grey system model[J]. Applied Mathematical Modelling, 2013, 37(9):6577-6583.

[7] Cui J, Liu S, Zeng B, et al. A novel grey forecasting model and its optimization[J]. Applied Mathematical Modelling, 2013, 37(6):4399-4406.

[8] Mao S, Gao M, Xiao X, et al. A novel fractional grey system model and its application[J]. Applied Mathematical Modelling, 2016,40(7):5063-5076.

[9] 杨杰,翁文国. 基于改进无偏灰色模型的燃气供气量的预测[J]. 清华大学学报,2014,54(2):145-148.

[10] 刘思峰,杨英杰. 灰色系统研究进展(2004—2014)[J]. 南京航空航天大学学报,2015,47(1):1-17.

[11] Liu S, Yang Y, Xie N, et al. New progress of Grey System Theory in the new millennium[J]. Grey Systems, 2016, 6(1):2-31.

[12] Yang Y, Liu S, John R. Uncertainty representation of grey numbers and grey sets[J].IEEE transactions on cybernetics, 2014,44(9):1508.