基于马尔科夫链模型对河流径流量预测探析
(辽宁省鞍山水文局,辽宁 鞍山 114039)
1 概 述
中长期洪水预报是建立在洪水的形成和运动的基础上,利用历史和实时的水文气象资料,来预测未来某一段时间的洪水发展趋势,是防灾减灾的一项重要的非工程措施。在多年的研究和实际的防洪工作中,丹东的洪水预报在理论和实践经验方面取得了很大的成就。针对东部地区洪水预报模型的特点,编制了主要河道控制站的实时洪水预报方案,开发了许多实用的在线实时洪水预报系统,为防洪决策提供了科学依据。近年来,对水文预报的要求越来越高,不仅需要正确的短期预测和周期较长的中期和长期的预测,更需要定性的预测和定量的预测。
马尔科夫预测模型是应用马尔科夫链的基本原理和方法来分析研究时间序列的变化规律,从而预测其未来变化趋势的一种技术,适合于随机波动较大的预报问题。本文根据大洋河年径流系列数据,应用马尔科夫链定性预测模型,预报未来年份的年径流总量的趋势。
大洋河发源于鞍山市岫岩县的唐帽山,流经岫岩、凤城、东港3县(市),在东港市大孤山马家坨子附近注入黄海,全长201.7km,流域面积6208km2。河床构造,上游多为卵石、粗砂,中游砂砾,下游为中细砂。河道平均坡度1.1‰,一般河宽300~400m。
沙里寨水文站是大洋河流域重要控制站,其积水面积为4810km2,干流河长157km,该站距河口44.7km,河道平均比降为1.4‰,1957年6月建站,具有实测水位、流量资料。据调查历史上该断面曾经发生较大洪水有3次,分别为:1888年8月、1937年8月及1960年8月,最高洪水位分别为104.79m、102.93m、102.83m,推求最大洪峰流量分别为15600m3/s、11800m3/s、12900m3/s。该站断面河道顺直,河床为细沙组成,具备了高洪测流的条件。
2 马尔科夫预测模型
马尔科夫过程是一种较普遍的随机过程,其特点是后效性。
如果对时间t的任意n个数值(n≥3),在条件X(ti)=xi(i=1,2,…,n-1)下,X(tn)的分布函数恰好等于在条件X(tn-1)=xn-1下X(tn)的分布函数,即
F(xn;tn|xn-1,xn-2,…,x1′;tn-1,tn-2,…,t1)
=F(xn;tn|xn-1;tn-1)(n=3,4,…)
(1)
则称X(tn)为马尔科夫过程,简称马氏过程。
马尔科夫过程的统计特性是由转移概率和初始分布所确定。状态和时间参数都是离散的马氏过程称为马尔科夫链或马氏链,它是马尔科夫过程的一种特殊情况。
马尔科夫预测模型是一种定性预测,表明未来发生状态的水文时间序列,首先进行时间序列划分是建立模型的关键。
设有预报对象素值序列x1,x2,…,xn,与其多年均值之差除以多年均值的百分数(距平值)为
(2)
式中di——xi的距平值,%;
xi——要素值;


(3)

Ni——状态E1出现的总次数。
由转移概率构成的k步状态转移概率矩阵为
(4)
其中,p(k)=pk。
设第0步处于状态Si的概率为Ai(0),从状态Si转移到状态Sj的概率为pij,在第一步处于状态Sj的概率为Ai(1),按照贝叶斯公式
P(A,B)=P(A)P(B/A)
(5)
Aj(1)=Ai(0)pij
(6)
若从第n步推广到n+1,则有
Ai(n+1)=Aj(n)pij
(7)
此式被称为马尔科夫预测模型,它表示只要知道状态转移概率矩阵,就可根据初始时刻处于各状态的概率来预测以后任一时刻各状态的概率。
随着过程发展,初始阶段的影响将逐渐消失,系统在n时刻处于状态Sj的概率与初始状态无关,仅取决于转移概率矩阵,因此,当n→时,绝对概率分布p(n)收敛于一个极限概率p,
(8)
这时,系统趋于一个稳定状态。
3 年径流总量的动态预测
大洋河是鞍山和丹东地区的重点防汛区域,该区域对防洪、防汛的要求是:确保下游两岸河堤在设计标准20年一遇的堤防安全,因此,做好沙里寨站径流预报就显得非常重要。本文选取沙里寨站1985—2014年共30年的年径流总量数据,利用马尔科夫预测模型进行预测。大洋河沙里寨站历年径流量过程见下图。

年径流量过程图
为了让预测数据更加真实可靠,根据丹东地区的实际情况,对大洋河历年径流过程情况进行定性分析,划分5个等级,即丰水、偏丰、正常、偏枯、枯水,具体各个等级定量值见表1。

表1 丹东地区年径流总量等级参考
根据沙里寨站1985—2014年的年径流总量数据,计算多年平均径流量值以及距平值,按照表1将每年上、下半年分为两个阶段进行丰平枯分类统计,其中枯水14个、偏枯10个、正常12个、偏丰12个、半水12个,见表2。

表2 数据分类
利用转移概率矩阵计算方法,建立一步转移概率矩阵如下:
根据一步转移概率矩阵,可求得二步转移矩阵和三步转移矩阵如下:
由贝叶斯公式可以计算出2015年年径流总量的状态概率向量为
同理,利用二步转移矩阵与三步转移矩阵,可以计算出2012年与2013年年径流量状态概率(见表3),它表明预测年径流量可能出现各等级的可能性。
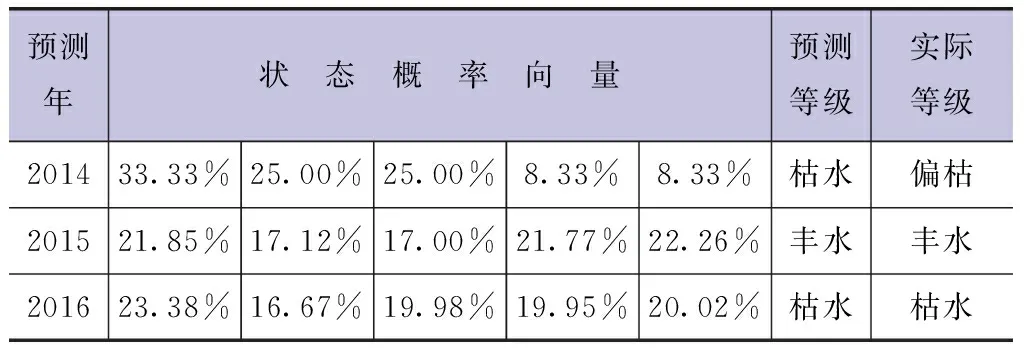
表3 预测年径流量状态概率
表3的预测结果表明,2014年预计出现枯水,2015年预计出现丰水,2016年预计出现枯水。这些结果与实际情况基本相符。可见,利用马尔科夫链模型定性预测年径流量等级是可行的。
4 结 语
本文利用马尔科夫链模型进行大洋河径流预测,作为一个中长期预报的方法进行了尝试,可以发现,马尔科夫链预测模型对过程的状态预测效果良好。鉴于此方法的可行性,今后在防洪调度、水利、水电、灌溉工程管理调度中,都可以应用上述方法进行中长期预报。马尔科夫链模型既可应用于流域定性预报预测,也可应用于趋势预报。
[1]李彬,袁鹏,常江.GM(1,1)改进模型在年径流量预测上的应用[J].东北水利水电.2006(2).
[2]王义民,于兴杰,畅建霞,等.基于BP神经网络马尔科夫模型的径流量预测[J].武汉大学学报(工学版),2008(5).
[3]王玲,黄国如.基于径流分类的日径流量预测神经网络模型[J].灌溉排水,2002(4).
[4]何万科.基于灰色系统理论的千河枯水年预测[J].水资源与水工程学报,2008(2).
[5]胡敬鹏,周新志,艾龙.都江堰灌区渠首优化配水模型探讨[J].水利科技与经济,2006(1).

