集装箱码头泊位、岸桥和集卡协同调度优化

田 星，孟庆柱

（1.武汉理工大学 物流工程学院，湖北 武汉 430063；2.天津东方海陆集装箱码头有限公司，天津 300456）

1 引言

对集装箱码头来说，泊位、岸桥和集卡是三种重要的基础资源，泊位分配、岸桥配置和集卡调度对提高集装箱码头的运作效率至关重要。泊位分配的目的是为了更好地利用有限的泊位资源，减少船舶在港产生的费用；岸桥是码头上比较昂贵的资源，岸桥调度指在满足岸桥位置约束的条件下合理配置岸桥的数量，以减少岸桥的闲置时间，提高岸桥的利用率；集卡运输集装箱在岸桥和堆场之间移动，集卡数量过多，会造成空间有限的堆场的拥堵，同时增加集卡的闲置率，降低集卡的作业效率，而集卡数量不足，会造成集装箱运输的延迟，从而降低了岸桥的作业效率。这三种资源紧密相关、具有联动关系，每种资源的调度都会对其它资源的调度产生影响。对港口来说，在原有硬件基础设施上，单独对其中某种资源进行调度优化，并不能实现所有资源的最优化利用，不能达到集装箱码头整体物流作业效率的最优化。同时考虑船舶泊位分配、岸桥配置和集卡调度这三个作业环节，协调好三个作业环节之间的关系，从整体上对三种资源进行协同调度，才能尽可能达到集装箱码头整体物流作业效率的最优化，从而提高港口的运营效率。

近年来，国内外许多学者针对集装箱码头一种资源的调度优化问题展开了研究。在泊位调度方面，Imai[1]针对离散型泊位船舶动态实时靠泊问题，以船舶在港时间最小为目标构建了混合整数规划模型，然后用启发式算法进行求解；Lim[2]给出了泊位调度问题是NP完全问题的证明，并以泊位闲置率最低为目标，把连续泊位调度问题转化成二维装箱问题进行研究；许欢[3]等以在港作业时间最短为目标，将实际到港时间作为决策变量建立了泊位分配数学模型，并用实际算例进行了验证。在岸桥调度方面，Daganzol[4]是最早开始进行研究的学者，他建立了混合整数规划模型来合理配置每艘船的岸桥作业线；Kim和Park[5]在固定船舶装卸量的前提下，以作业时间最小为目标建立了混合整数规划模型，运用贪婪随机自适应算法和分支定界方法进行求解；曾庆成[6]在Kim的模型基础上进行了改进，运用改进的遗传算法来优化岸桥配置问题。在集卡调度方面，Bish[7]运用启发式算法以船舶在港时间最小为目标提出了集卡动态调度模型；Han[8]从平衡码头堆场资源的角度出发，运用启发式算法对中转型集卡调度问题进行了研究；曾庆成[9]借助Q学习算法对不同条件下的集卡调度问题进行求解，求得相关调度策略；李广儒等针对面向整个港口的集卡作业问题，提出了一个动态蚁群算法来进行求解，使算法更加具有时效性[10]。

针对集装箱码头多种资源的优化调度问题，Bierwirth和Meisel[11]指出可以用三种方法来求解泊位、岸桥和集卡的调度问题，即顺序法、反馈回路法和同步法，顺序法和反馈回路法都需要建立两个模型，实现分层调度，而同步法能够实现三种资源的协同调度，将两个模型合并为一个模型进行求解；冯春焕[12]在泊位连续和装卸混合作业的前提条件下，以船舶在港时间与集卡装卸集装箱运输作业时间之和最小为目标，构建了一个三者协同调度的整数线性规划模型，利用Lingo求解得到了船舶的最佳泊位、最优岸桥分配数量以及基于运输时间最短的集卡行驶路径，并将结果与之前的三种资源单独调度的研究相比较；单浩[13]以计划期内所有到港船舶的作业费用最少为目标，建立了三者协同调度优化的数学模型，然后运用遗传算法进行求解，验证了模型的有效性；ZJ.Gao和CJ.Wu等[14]不仅考虑了这三种资源，也将堆场龙门吊纳入考虑范围，以最小化船舶在港时间、岸桥作业时间、集卡运输时间和堆场龙门吊的作业时间为目标建立了一个数学模型，并设计了遗传算法进行求解，具有一定的参考意义；A.Karam[15]在给出了泊位调度问题（BAP）与岸桥、集卡联合调度问题两个模型的基础上，以最小化集装箱处理成本为目标，建立了一个三者协同调度的混合整数规划数学模型，集装箱处理成本包括三个方面：船舶停靠位置最佳泊位的惩罚成本、船舶到港时间晚于预期到港时间的惩罚成本和船舶离港时间晚于最晚离港时间的惩罚成本；A.Karam和A.B.Eltawil[16]认为集卡数量的多少对船舶整体作业时间有重大影响，他们在集卡数量有一定限制的条件下提出了一个协同调度的混合整数规划模型，并对文中的排队模型进行了验证。以上针对泊位、岸桥和集卡协同调度的研究都是在一定前提条件之下进行的，具有一定的代表意义。本文通过对我国T集装箱港口进行实地调研，建立了一个泊位、岸桥和集卡协同调度的数学模型，并利用该码头的实际数据，运用CPLEX进行求解验证。

2 问题描述

在T港口的实际操作过程中，船舶到港后先在锚地临时停靠等待泊位，获得泊位后进行靠泊操作，当船舶停靠完毕后，为该船配置的岸桥和集卡都已就位，岸桥立即开始进行集装箱卸载作业，将进口箱卸载到集卡上，由集卡运输到堆场的指定区域，然后集卡再空箱返回岸边。本文的研究不能覆盖码头所有作业时间内的操作，以48h为一个研究周期，时间单位精确到分钟，对一个周期内船舶到港、停靠以及后续的作业展开研究。

通过在T港口进行实地调研，从该港口提供的昼夜作业计划表中提取真实数据进行分析，得到了该码头在日常作业中，船舶待卸载的集装箱数量与分配的岸桥数量之间的关系，本文以均衡每艘船的作业时间为目的，设置了一个常数k，使得待卸载的集装箱数量与常数k的比值即为每艘船舶分配的岸桥数量，将建立的数学模型转化为整数线性规划模型。在本文中，若船舶的实际离港时间早于最晚离港时间，则延误时间为0，若实际离港时间晚于最晚离港时间，则延误时间为实际离港时间与最晚离港时间的差值；船舶待装卸的集装箱总量除以每台岸桥的作业效率即为船舶服务的岸桥总作业时间；由于每辆集卡每次只运输一个集装箱，船舶待卸载的集装箱总量乘以集卡运输往返时间即为船舶服务的集卡总作业时间；在实际操作过程中，岸桥的作业成本比集卡的作业成本高很多，为了减少总成本，应该让集卡等待岸桥，避免岸桥等待集卡情况的发生，对于任意船舶来说，每一台岸桥的作业时间减去每一辆集卡的运输时间即为平均每辆集卡等待岸桥的时间，那么，集卡等待岸桥的总时间为：每一台岸桥的作业时间减去每一辆集卡的运输时间再乘以每台岸桥分配的集卡数量，再乘以为船舶服务的岸桥数量。

3 数学模型

3.1 模型假设

本文模型的建立基于如下假设条件：（1）码头岸线为连续型，不考虑任何物理条件对泊位的约束和限制；（2）船舶在港过程中可能产生的移泊都忽略不计；（3）所有到港船舶的到港时间和待卸载的集装箱量是已知的；（4）只对进口箱即需要卸载的集装箱进行研究；（5）岸桥为轨道式并处于同一轨道上，具有相同的移动速度；（6）所有岸桥具有相同的工作效率，其故障和休息时间忽略不计；（7）任意两台岸桥之间的作业不会对彼此产生干扰；（8）每台岸桥配置的集卡数量相同且已知；（9）码头上可供使用的集卡数量充足；（10）每辆集卡每次只能运输一个集装箱；（11）集卡运输不同集装箱到不同堆场的往返时间相同且已知；（12）当船舶上所有的进口箱卸载完毕后，为该船舶服务的岸桥和集卡才能离开去为另一艘船服务。

3.2 模型参数定义

为了方便模型的构建，下面对建立模型所需的相关参数进行定义。

（1）集合符号定义：V={v1,v1,...,vk}，为船舶集合；Q={q1,q1,...,qn}，为岸桥集合；WB(t)为在t时刻，等待靠泊的船舶集合；BA(t)为在t时刻，在港的船舶集合。

（2）参数符号定义：T为研究周期；L为可用靠泊岸线的长度；Nq为码头可用岸桥总数；Nt为码头可用集卡总数；rq为岸桥q的单位作业效率；t为集卡运输集装箱一次的往返时间；nqv为船舶v分配的岸桥数量；ntq为岸桥q分配的集卡数量；lv为船舶v的长度；为船舶v的到港时间；为船舶v的最晚离港时间；NCv为船舶v待装卸的集装箱数量；为船舶v的在港单位作业时间成本；为船舶v等待泊位的单位作业时间成本；为船舶v延迟离港的单位作业时间成本；Cq为岸桥q的单位作业时间成本；Ct为集卡t的单位作业时间成本；为集卡t等待岸桥q的单位作业时间成本。

（3）直接变量定义：bv为船舶v的实际停靠位置；Nhv为船舶v船首所对应的岸桥的编号；为船舶v开始作业（靠泊完成）的时间；为船舶v的实际离港时间。

3.3 模型建立

本文将时间类优化目标转化为作业成本优化目标，即以集装箱码头整体物流作业总成本最小为优化目标来构建数学模型，具体如下：

式（1）为目标函数，目标为整体物流作业总成本最小，具体包括6大主要成本：船舶在港时间成本、船舶等待靠泊的时间成本、岸桥作业的时间成本、集卡作业的时间成本、岸桥等待集卡的时间成本和船舶延误成本。式（2）为将间接变量带入式（1）后，得到的简化目标函数。

式（3）-（8）为约束条件：式（3）为对于任意时刻t，靠泊的船舶总长度小于等于码头岸线的总长度；式（4）为对于任意两艘船v、v'，不能共用同一个泊位，即不允许出现重叠靠泊的现象；式（5）为对于任意时刻t，同一个岸桥q只能为同一艘船服务；式（6）为对于任意时刻t，为船舶v服务的岸桥数量不能大于码头的岸桥资源总数；式（7）为对于任意时刻t，为岸桥q服务的集卡数量不能大于码头的集卡资源总数；式（8）为对于任意船舶v，船舶完成靠泊后才能进行装卸操作。

4 算例分析与求解

4.1 算例介绍

T港口的码头岸线为连续型，总长1 200m，研究周期为48h（2 880min），在一个周期内共有15艘船在该码头进行卸船作业。该码头配有9台岸桥，编号为1至9，每台岸桥的作业效率为0.5箱/min，进行集装箱运输作业的集卡一共有44辆，集卡运输集装箱的往返时间为4min，每台岸桥配置的集卡为4辆。各个作业环节的单位作业时间成本为：船舶等待泊位的单位作业时间成本为283元/min，船舶在港的单位作业时间成本为200元/min，船舶延迟离港的单位作业时间成本为250元/min，每台岸桥的作业时间成本为40元/min，每辆集卡的作业时间成本为10元/min，集卡等待岸桥的单位作业时间成本为10元/min。

根据一个周期内船舶到港的先后顺序对船舶进行1-15的编号，各船舶的长度、到港时间、最晚离港时间、待卸载的集装箱数量等信息见表1。

表1 到港船舶的相关信息表

4.2 结果分析

利用ILOG CPLEX求解算例得到最优解，即在该周期内，到港船舶的泊位位置、开始作业时间、实际离港时间、分配的集卡数量以及分配的岸桥数量和编号，见表2。

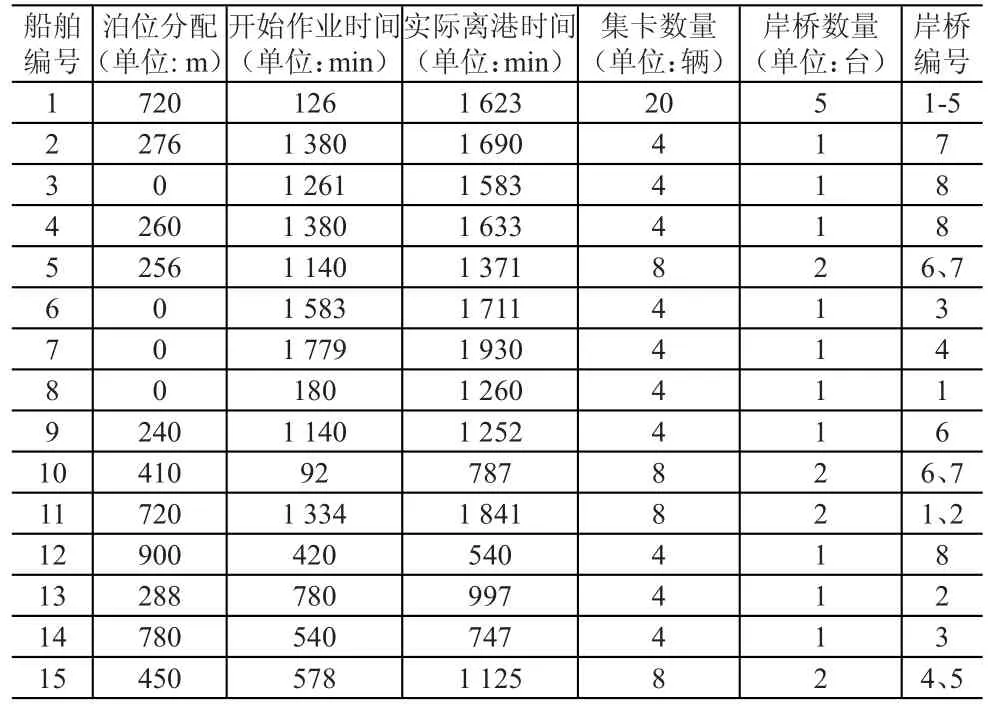
表2 案例最优分配方案

利用ILOG CPLEX求解显示上述分配结果是最优的，得出的该集装箱码头的整体物流作业总成本最小值为1 845 926元。

本文选取的算例是T港口的码头在48h内产生的真实数据，为了验证本文模型的有效性，将本文求解得到的最优解与实际操作过程进行比较。在实际操作过程中，到港船舶的相关信息见表3。

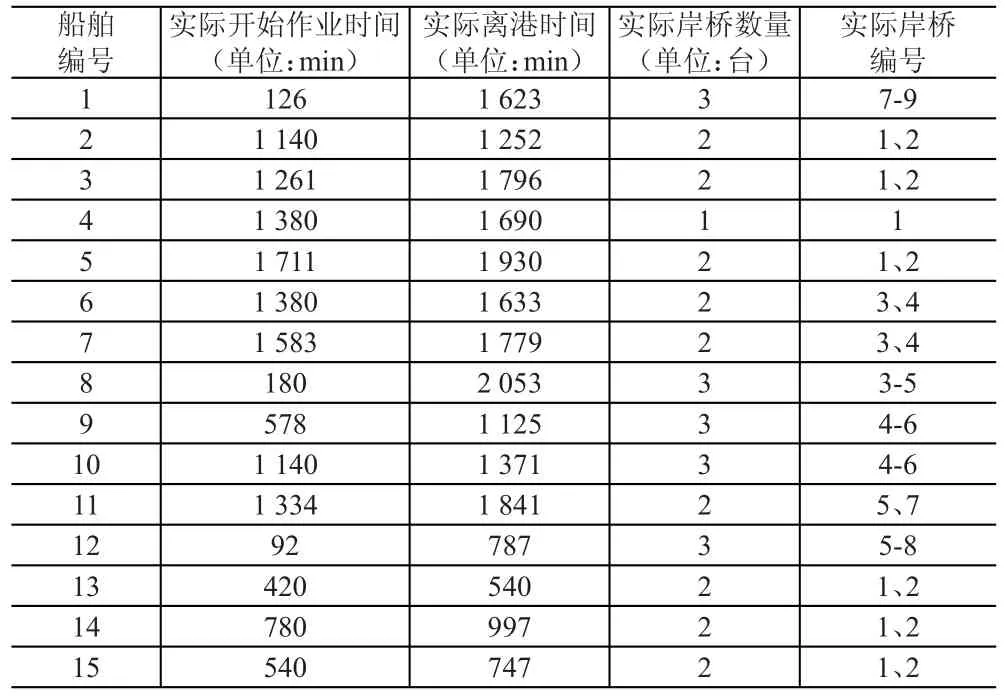
表3 实际操作过程中船舶相关信息

利用表1和表3中相关数据，根据式（2）求得实际操作过程中的整体物流作业总成本为：2 845 410元。该成本比本文求得的最优成本大得多，可以得到以下结论：

（1）本文用ILOG CPLEX求解算例，并在较短时间内得到了最优解，证明了建立的整数线性规划数学模型是有效的，表明精确算法也可以用来求解泊位、岸桥和集卡的协同调度问题；

（2）根据本文数学模型求得的总成本比实际操作过程的总成本减少了35%，如果将本文建立的模型运用在实际操作作业中，能有效降低码头作业成本，提高作业效率，具有一定的实际意义。

5 结论

在集装箱码头上，单独对泊位、岸桥和集卡中的某一种资源进行优化调度，不能实现码头整体物流作业效率的最优化，只有同时考虑三种资源的协同调度优化，才能尽可能达到码头整体物流作业效率的最优。基于上述思路，针对泊位、岸桥和集卡的协同调度优化进行了研究，以整体物流作业成本最小为目标，提出了协同调度的整数线性规划数学模型，并以国内某大型集装箱港口T的真实数据为算例，运用商业软件ILOG CPLEX进行求解，在可接受的时间内求得了最优解，并将求得的结果与实际操作过程进行对比，表明得到的最优解在实际操作过程中是可行的，验证了模型的有效性和准确性。如果将本文建立的模型运用在T码头实际操作过程中，能够有效降低码头作业成本，提高作业效率，具有一定的实际意义。

本文的研究还存在一些不足之处，后续的研究将从以下几个方面展开：（1）本文选取的算例相对较小，将来考虑扩大算例的规模来验证模型的有效性，比如考虑对一周、一月内到港的船舶开展研究；（2）在扩大算例规模的条件下，如果运用本文的模型和算法求解较慢，考虑改进模型，或者运用一些启发式算法来进行求解。

[参考文献]

[1]Akio Imai,Etsuko Nishimura,Sryatos Papadimitriou.The dynamic berth allocation problem for a container port[J].Transportation Research Part B,2001,35:401-417.

[2]Lim A.The berth planning problem[J].Operations Research Letters,1998,22(2):105-110.

[3]许欢,刘伟,刘诗.低碳经济下的港口泊位分配模型及其算法实现[J].计算机工程与应用,2014,(18):47-48.

[4]Daganzo C F.The crane Scheduling Problem[J].Transportation Research.1989,23(3):159-175.

[5]Kim K H,Park Y M.A crane scheduling method for port container terminals[J].European Journal of Operational Research,2003,156(3):752-768.

[6]曾庆成,高宇.集装箱码头装卸桥调度优化模型与算法[J].计算机工程与应用,2006,(32):217-219.

[7]Ebru K Bish,Thin-Yin Leong,Chung-Lun Li,et al.Analysis of a new vehicle scheduling and location problem[J].Naval Research Logistics,2001,48(5):363-385.

[8]Yongbin Han,Loo Hay Lee,Ek Peng Chew,et al.A yard storage strategy for minimizing traffic congestion in a marine container transshipment hub.OR Spectrum,2008,30(4):697-720.

[9]曾庆成.集装箱码头装卸作业集成调度模型与方法[D].大连:大连海事大学,2008.

[10]李广儒,杨大奔,任大伟.集卡动态调度路径优化算法[J].交通运输工程学报,2012,12(3):86-91.

[11]Bierwirth C.,Meisel F.A survey of berth allocation and quay crane scheduling problems in container terminals[J].European Journal of Operational Research,2010,202(3):615-627.

[12]冯春焕.集装箱码头泊位—岸桥—集卡调度优化研究[D].大连:大连海事大学,2011.

[13]单浩.集装箱码头泊位、岸桥和集卡协同调度优化研究[D].大连:大连海事大学,2013.

[14]Guangfan Li,Chaohe Chen,Bifeng Jiang,et al.Research on the Optimization Model of Berth Allocation-Quay Crane Assignment-Truck Scheduling at Container Terminals[J].Applied Mechanics and Materials,2014,587-589:1 785-1 788.

[15]Ahmed Karam.Allocating berths,quay cranes and internal trucks in container terminals[A].the International Marine Transport&Logistics Conference(MARLOG 4)[C].2015.

[16]Ahmed Karam,Amr Eltawil.A new method for allocating berths,quay cranes and internal trucks in container terminals[A].5thIEEE International Conference on Logistics,Informatics and Service Science[C].2015.