柔体系统动力学算法中的形函数选择问题研究

赵　洋　王德石

（海军工程大学兵器工程系　武汉　430033）

1　引言

多柔体动力学研究机械与结构系统中的构件弹性、运动副变形与刚性运动的耦合动力学特性，其与多刚体动力学有相同的研究目的，即旨在解决动力学系统的仿真与控制正逆两类问题［1］。在发展刚体系统动力学的过程中，首先关心的是实时控制与仿真计算所需要的算法效率，所以利用分析力学的诸多原理［2～5］，建立了各种递推算法［2～4］；随着计算机芯片技术的进步，算法的效率不再是研究的重点，并且根据力学原理的等价性，无论采用何种原理都可以获得系统的一般形式的封闭动力学方程［1，5］。在机器人［6］、航天器［7］、运动生物力学［8］、以及火炮机构［9～13］等诸多领域，利用多刚体动力学理论与算法，已经可以建立所需的动力学模型，并且用于分析系统的响应或为系统设计实时动力学控制算法。

在多刚体动力学基础上进一步考虑系统中构件或铰链的变形特性，既是工程中的需求，也是提高仿真与控制算法精度的理论需要。周起钊在文献［13］中表明：“带有太阳能帆板的航天器在将帆板视为刚体的情况下系统是稳定的，而考虑帆板的弹性时系统就可能是不稳定的”，并且在柔性体系动力学发展之早期，就指出了多柔性体系统动力学的重要研究问题［14］。其一是浮动坐标系的选择问题，它决定了系统动力学方程的耦合程度［1，13～15］；其二是弹性体或铰链变形的描述问题，它决定着仿真与控制算法的运算效率与计算精度［1，14］。浮动坐标系和弹性体的形函数带来的这些问题，理论上似乎比较完善，但在工程领域遇到的问题是，针对某一领域的仿真与控制问题，究竟如何选取它们至今不够明确。目前在各个领域如航天器与火炮的仿真与控制，基本上是给定一种方式建立动力学模型，简化处理后，设计相关算法。事实上针对不同的应用情形，浮动坐标的建立与弹性体的变形及其控制要求是不尽相同的，尤其是形函数的选择，不同的应用领域的精度要求决定了假定形函数的复杂程度以及计算效率的高低，例如火炮的身管变形与航天器太阳能帆板就不必取同一计算精度的形函数。这样的问题至今并未得到足够的研究。

本文针对形函数影响数值计算精度和效率问题，在分析浮动坐标系建立于指定铰链处的基础上，首先建立多柔性体系统一般形式的动力学方程，然后针对三种形式的形函数，通过分析动力学方程中的系数矩阵，讨论不同的形函数导致的柔性体系统仿真与控制的计算精度与运算效率。最后通过一个双连杆算例对采用不同类型变形函数的动力学方程进行仿真计算，以期为柔体系统仿真与控制中的形函数选择提供参考。

2　多柔体系统运动学

考虑系统中任意两个铰链连接的柔性体，建立系统的坐标系，如图1所示。惯性坐标系位于O点，Oixiyizi为第i个物体的浮动坐标系。取浮动坐标系原点Oi位于第i-1个柔体与第i个柔体之间的铰链上，其在惯性坐标系中的位置向量为ROi。取第i个物体为研究对象，柔性体上任意一点P的位移为刚性运动ro与弹性运动uf之叠加。

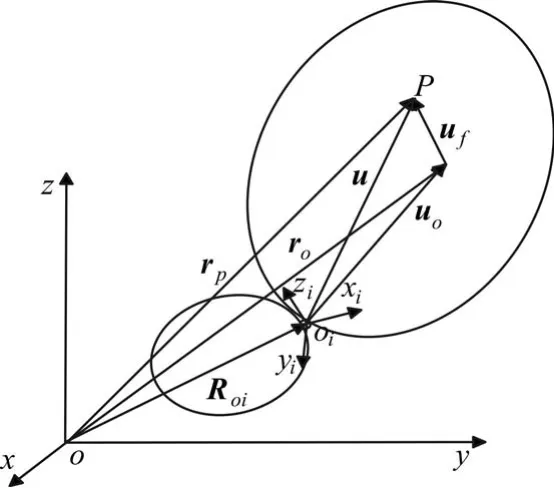
图1　两个铰接的柔性体

在动坐标系中，令uO为未变形时的位置向量，uf为任意变形引起的位置向量，且令u为P点相对于动坐标系的位置向量，则有u=uO+uf。当任意的P点遍历柔体时，柔体的位移形成一个位移场Φ(x，y，z)，且该位移场是相容和完备的。为了进一步描述物体的变形模式，取形函数矩阵Φ=[Φ1，Φ2，…，Φn] ，则弹性体上各点的变形量 uf可表示为uf=Φqf，其中：qf为对应于变形的广义坐标。在惯性坐标系中，点P的位置矢量可表示为

式中：A为动坐标系相对于惯性坐标系的旋转变换矩阵。对式（1）求导，可得P点速度矢量为

由欧拉参数的定义［15］，旋转变换矩阵可表示为A=ÊĜT。设 Ȧu=-2Au͂ĜṖ=BṖ。 P 点速度矢量可表示为矩阵形式：

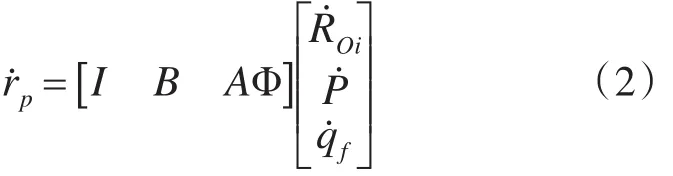
式（2）确定了任意柔性体上任意一点的速度矢量，可以看出形函数影响柔性体任意一点的速度矢量和动能，形函数的选择对柔性体系统动力学方程的求解至关重要。

3　动力学基本方程

1）柔性体i的动能计算。由任意P点速度矢量表达式，可求得柔性体i的动能为

2）柔性体i的势能计算。由弹性变形引起的内力的虚功为

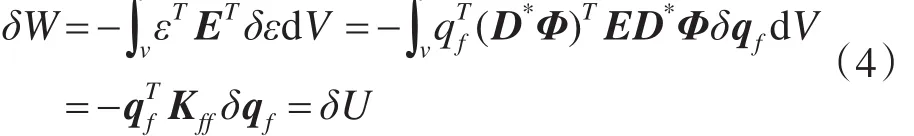
式中：D*为微分算子矩阵，E为弹性模量矩阵。ε=D*uf=D*Φqf，σ=Eε=ED*Φqf。 Qe=-K为弹性体变形引起的弹性力的广义力，而Kff=∫v(D*Φ)TED*Φd V 为对应于广义坐标 qf的弹性体的刚度矩阵，是对称正定矩阵。弹性体的应变能为

3）广义力的计算。设作用于柔体上一点的集中力为F=F(q，t)，在其作用点虚位移上的虚功为

通过推导柔体系统动力学方程的质量矩阵M和刚度矩阵K表达式可以看出，在指定浮动坐标系下，柔体系统动力学方程形式以及各系数矩阵元素相同，所以方程的解耦程度相同，说明形函数的选择与方程的解耦程度无关。不同形式的形函数导致不同复杂程度的系数矩阵以及不同数量的广义坐标，因而形函数影响动力学方程计算精度和效率。按照目前采用的假设方法，虽然可以得到问题的解，但是其精度估算是非常困难的，误差也是时变函数，这正是柔体动力学的困难所在。

4　柔性体的形函数

柔体在运动过程中本身的构型是不断变化的，采用离散化手段，把柔性体相对变形表示成N个广义坐标qi(i=1，…，N)的线性组合，获得变形一般位移表达式为

其中：Φ为一般形式的形函数，它只与位置有关。假定合适的形函数是离散化的核心问题，期望选取的形函数尽可能描述物体的实际变形，静力变形、有限元模型和振动模态是主要的三种形函数。

考虑图2所示的双连杆机构，m1和m2为端部集中质量，两连杆均为均匀欧拉梁，其质量分别为M1、M2，长度分别为 l1、l2，刚度分别为 EI1、EI2。下面分别以三种形函数描述连杆变形。

图2　双连杆平面运动机构

情形1：以静力变形为形函数。静力变形模型是取物体在外力包括重力作用下的静变形作为其假设变形模式。连杆可等效为悬臂梁模型，受自身重力和端部集中力作用。由材料力学知识可得，连杆在受均布载荷（自身重力）和端部集中力作用下的柔度分别为

采用静力变形模型描述柔性体运动中的弹性变形，比使用刚体模型计算时的精度有所提高。静力变形模型简单，所需广义坐标数量少，计算效率高。但以静力变形代替动力变形描述柔性体弹性变形，计算精度必然存在较大误差。

情形2：以有限元模型为形函数。有限元法是将具有复杂形状、边界条件和载荷的物体化整为零，分割为有限数量、有限大小且有一定规则形状的单元。属于i物体第 j单元上任意一点P的位移向量可表示为

式中：Nij为 j单元的变形模式或假设位移场，称为 j单元的形函数，为该单元的节点位移向量。在将所有单元拼装后，物体上所有节点的位移向量，就构成了该物体的弹性广义坐标。在图2所示模型中，将连杆等效为梁模型并划分为i个单元，单元长l，单元节点位移是节点的挠度和转角：

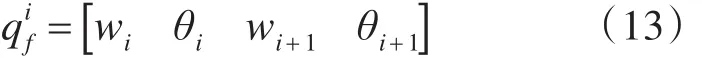
通过多项式拟合，可得到以单元节点位移表示的形函数：

在得到梁单元刚度矩阵、质量矩阵后，根据初始条件可组装成系统的刚度矩阵和质量矩阵，然后进行振动分析。在有限元模型计算中，单元变形模式Nij的选取有多种形式，可根据柔性体的材料、形状以及计算精度和效率限制等因素酌情选取。划分单元数量越多，广义坐标数量越多，计算精度越高，随之带来的问题是计算效率的下降。

情形3：以振动模态为形函数。振动模态是结构动力学中普遍采用的一种描述物体空间变形的方法。它通过引入模态向量和模态坐标来描述柔性体上任意点的变形，即

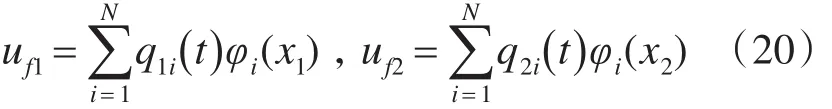
其中：φi(x)为杆件的第i阶振型，qi(t)为模态坐标。根据图2所示连杆的边界条件，连杆1、2的振型函数可取简支梁的振型函数，即(x)=sin。

可以根据先验的响应特征和精度要求，来考虑模态截断范围。一般情况下，低阶模态响应贡献大，高阶模态响应贡献较小在保证求解精度的前提下，可把贡献小的模态截去，以最大限度地缩减求解规模。

5　案例分析

设r1、r2分别为连杆1上点P1和连杆2上点P2在惯性坐标系中的位置向量，则系统的动能为

1）计算连杆1的动能。

坐标系的选取如图3所示，可得连杆1上任意一点P1的位置向量r1：

图3　连杆1示意图

连杆1的动能为

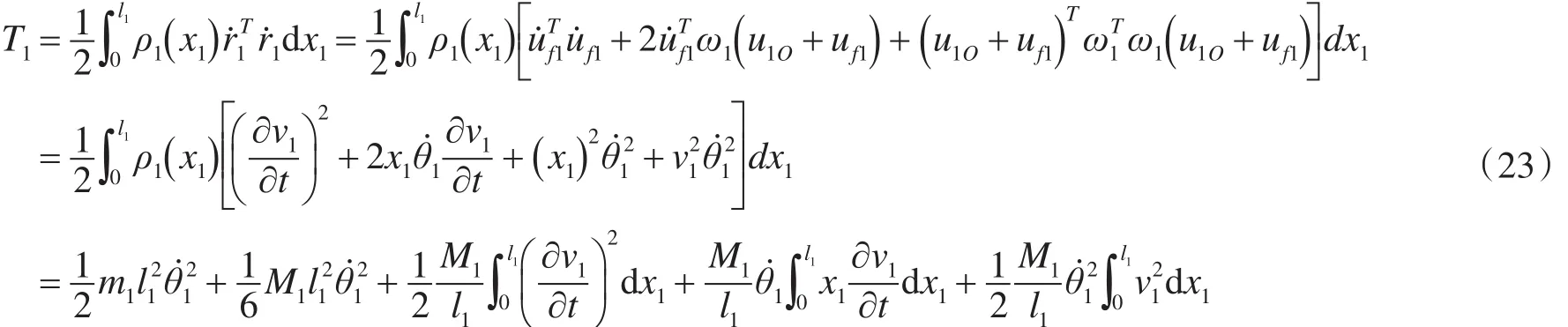
式中：v1为连杆1的挠度，连杆1的密度ρ(x)=11+mδ(x-l)。111

2）计算杆2的动能。

坐标系的选取如图4所示，可得连杆2上任意一点P2的位置向量r2：

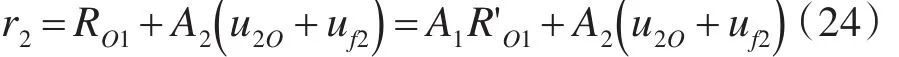
图4　连杆2示意图

连杆2的动能为

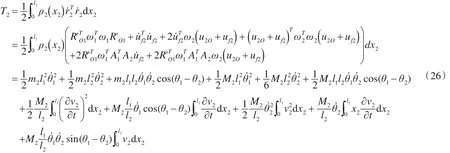
式中：v2为连杆2的挠度，连杆2的质量密度ρ(x)=22+mδ(x-l) 。222

情形1：以静力更正模型为例进行推导，将式（11）、（23）、（26）代入拉格朗日方程，可得质量矩阵M中非零元素的表达式为

由于以静变形代替杆件动变形，系统并未增加广义坐标，刚度矩阵K=0。双连杆系统重力势能为

双连杆系统的驱动力矩τ1(t)、τ2(t)分别为连杆1和连杆2的主动力，利用虚功原理可求得对应的广义力为

情形2：式（17）、（18）已推导出有限元模型中单元的质量矩阵M和刚度矩阵K，将单元质量矩阵和刚度矩阵进行组装，即可得到系统的质量矩阵和刚度矩阵，此处不再赘述。

情形3：以振动模态为例进行推导，取模态截断数n=3，杆件的前三阶振型函数为

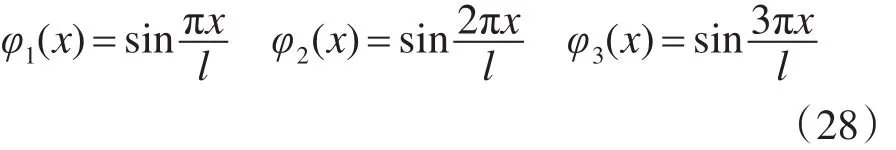
将式（20）、（28）、（23）、（26）代入拉格朗日方程，可得质量矩阵M中非零元素的表达式为

双连杆系统的驱动力矩τ1(t)、τ2(t)分别为连杆1和连杆2的主动力，利用虚功原理可求得对应的广义力为

分别以静力变形模型、有限元模型和振动模态描进行数值仿真，仿真参数如下：

假设初始时刻两杆均处于水平位置，且变形为零，初始条件为q(0)=0 ，q̇(0)=0。

取前三阶振动模态为参照，分别以静力变形模型、一阶振动模态、有限元模型和刚体模型，计算连杆角速度和末端位移与其之间的误差，仿真结果如图5～6所示。

图5～6表示刚体模型以及三种形函数下柔体模型中的连杆角速度误差。可以看出：由于在静力变形模型中，是以静力变形代替动力变形作为柔体的形函数，所以静力变形和刚体模型对柔体角速度的影响程度相同。刚体模型和静力变形误差较大，达到±0.14rad/s，柔性变形影响杆件的刚性转角，在精度要求较高的运动机械中，结构的柔性变形不可忽略。一阶振动模态的计算误差小于±0.05rad/s，计算精度明显提高，对于一般机械结构，在保证求解精度的前提下，可截去高阶模态，以最大限度地缩减求解规模。有限元模型误差小于±0.02rad/s，计算精度最高，但由于每个单元都对应着数个广义坐标，系统动力学方程系数矩阵维数高，计算效率最低。

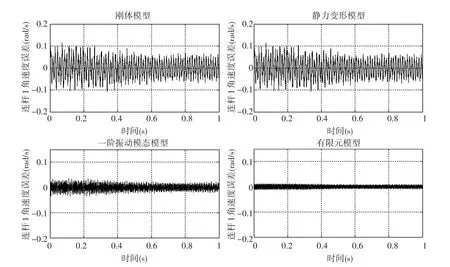
图5　连杆1角速度误差

图6　连杆2角速度误差

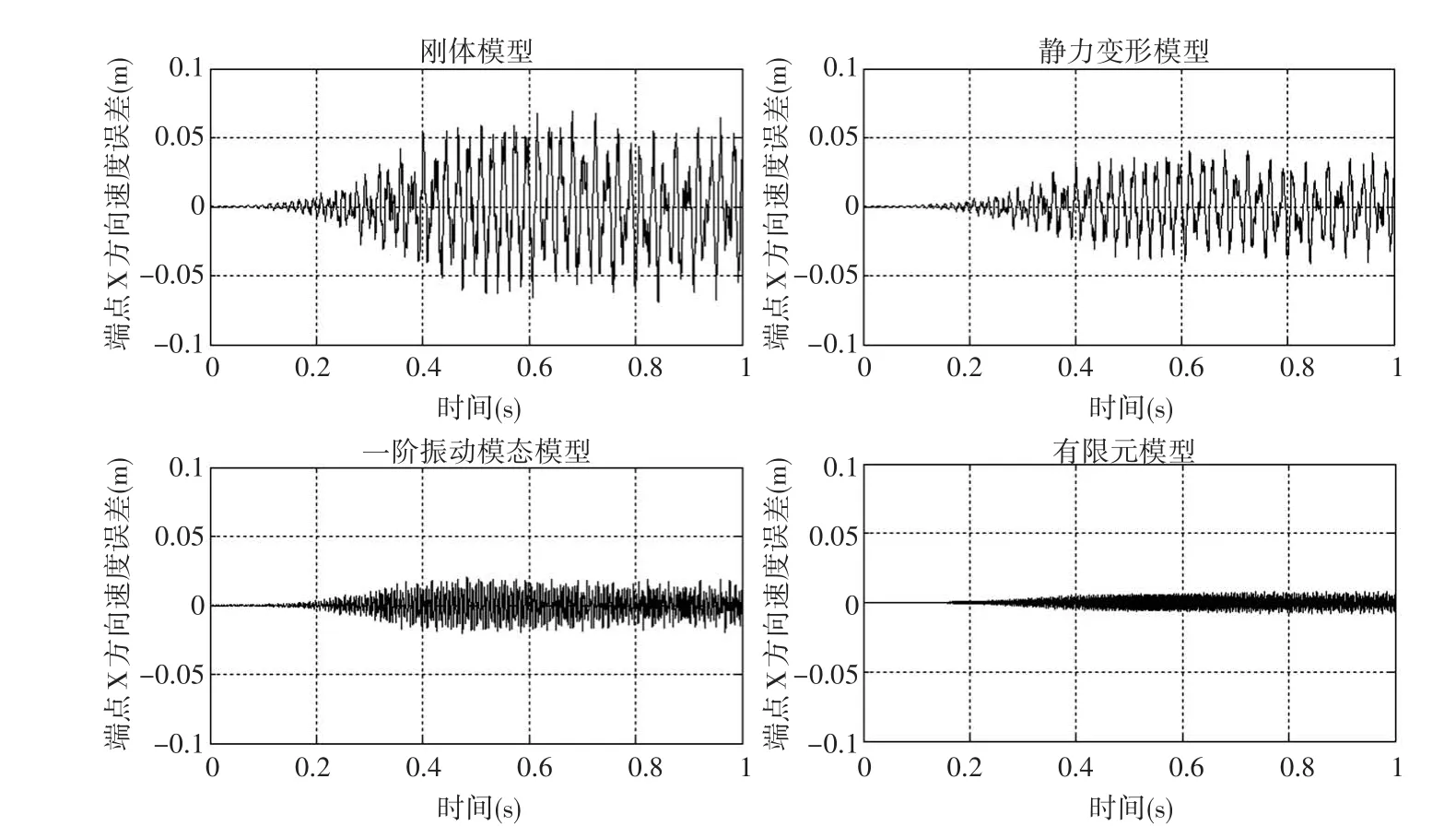
图7　端点X方向位移误差

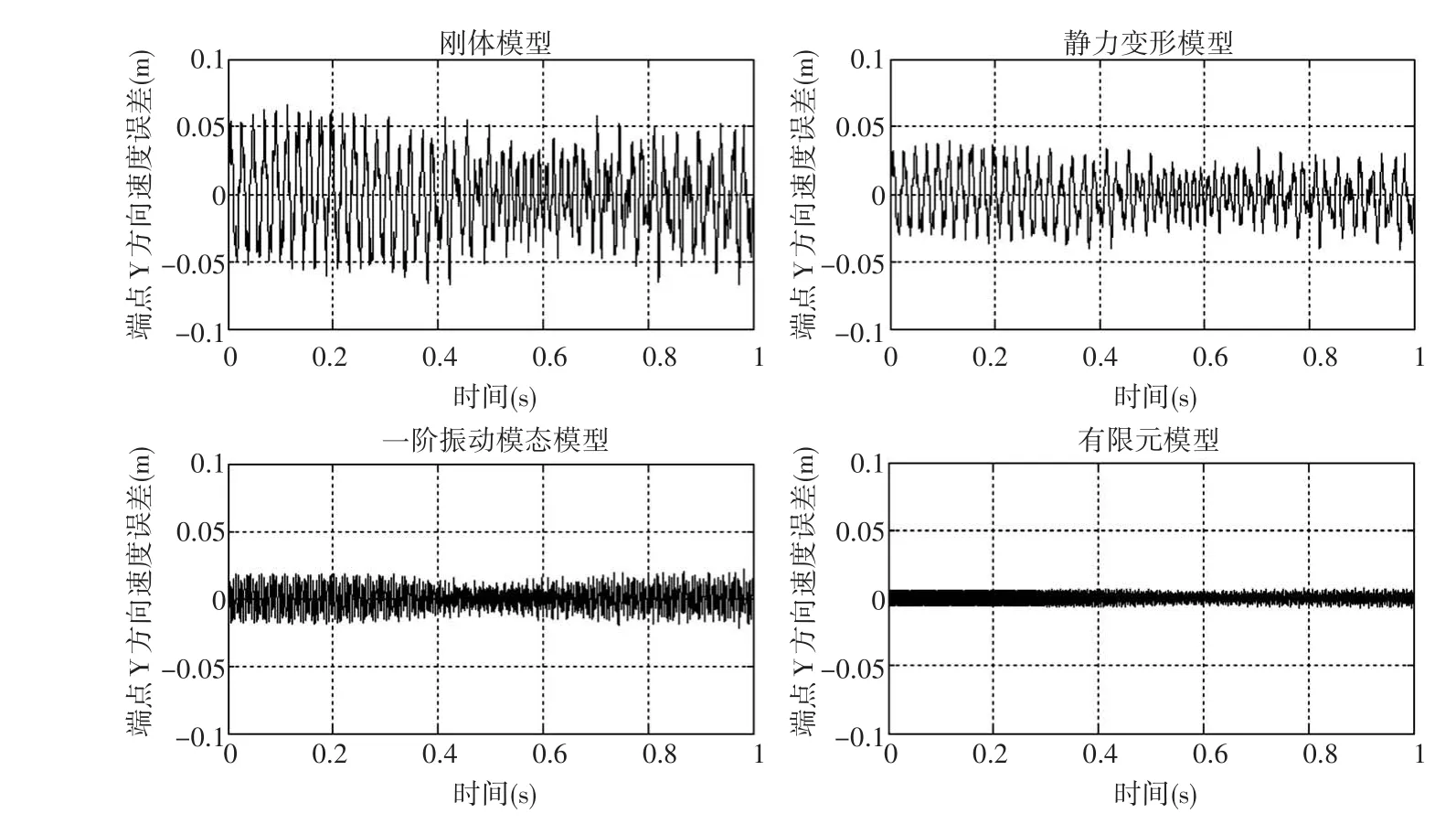
图8　端点Y方向位移误差

通过对比图7、8中刚体模型以及三种形函数下柔体模型中的端点位移误差，我们可以看出：由于杆件柔性的存在，杆件末端速度与按刚性所推算出来的末端速度存在偏差，X方向和Y方向的偏差可达到±0.07m/s。静力变形模型中，由于考虑了杆件的弹性变形，误差较刚体模型有所减小，但以静力变形代替动力变形作为柔体的形函数，计算误差相对于一阶振动模态和有限元模型仍然较大。一阶振动模态和有限元模型误差较小，并且随着模态截断数增大和划分单元数增多，计算精度提高，但广义坐标也随之增多，计算效率降低。此外我们还可以看到，除连杆的变形效应是必须加以考虑之外，杆的运动中包含着高频部分的振动，从而导致杆件的抖动，增大了对杆件的控制难度。

6　结语

本文针对形函数影响数值计算精度和效率问题，在分析浮动坐标系建立于指定铰链处的基础上，通过建立一般形式的动力学方程，分别讨论了形函数的三种形式并分析了三种形函数的特点。分析和案例表明：

在指定浮动坐标系下，柔体系统动力学方程解耦程度相同，即质量矩阵、刚度矩阵和阻尼矩阵有相同元素，说明形函数的选择与方程解耦程度无关。柔体系统动力学方程计算精度与浮动坐标系和方程耦合程度的关系不大，耦合程度主要影响方程复杂度，而形函数对方程计算效率和精度影响较大。

静力变形模型方程形式简单，计算效率最高，在计算杆件末段位移时，误差较刚体模型减小，计算角速度时与刚体模型误差相同。相比之下，有限元模型应用灵活，适合复杂结构的仿真计算。振动模态模型中模态截断数不同，导致计算结果不同。有限元模型和振动模态模型中的广义坐标数量和计算精度随着划分单元个数和模态截断数的增加而增加，计算效率也随之下降。

上述工作从理论公式推导与分析，并通过案例分析的不同侧面，详细给出了柔体系统弹性变形选取与方程计算精度和效率之间的变化规律，根据不同需求，可供柔体系统动力学的仿真与控制参考选用。

［1］王德石.火炮振动理论［M］.北京：兵器工业出版社，2015：111-114.WANG Deshi.Theory of Gun vibration［M］.Beijing：Weapons industry press，2015：111-114.

［2］遇立基，陈循介.操作机器人动力学与算法［M］.北京：机械工业出版社，1983：1-5.Popov.，E.L..Dynamics and Its Algorism for Manipulation Robot［M］.Beijing：Mechanical industry press，1983：1-5.

［3］WALKERMW.Efficient dynamic computer simulation of robotic mechanisms［J］.Measurement and Control，1982，104：205-211.

［4］王德石.惯量耦合补偿控制的递推算法［M］.北京：科学出版社，2002：122-130.WANG Deshi.Recursive algorism for the inertia compensation control［M］.Beijing：Science Press，2002：122-130.

［5］KANE TR，LEVINSON D A.The use of Kane's dynamical equations in robots［M］.New York：Mc Graw-Hill Book Company，1983：97-119.

［6］WITTERBURG J.Dynamics of systems of rigid bodies［M］.Stuttgart：B.G.Teubner，1977：107-111.

［7］ROBE TR，KANE TR，etal.Dynamics ofan elastic satellite［J］.Solid and Structure，1996（3）：333-352，691-703，1031-1051.

［8］HUSTON R L.Human body dynamics：impact，occupational，and athletic aspects［M］.Oxford：Claremont press，1982：59-62.

［9］WANG Deshi.Vibrations analysis for gun systems bymultibody dynamics［M］.New York：Academic Press，1999：111-116.

［10］王德石，史跃东.火炮振动分析与多体系统模型研究［J］.动力学与控制学报，2012，10（4）：304-323.WANG Deshi，SHIYuedong.Research on Artillery Vibration Analysis and Multi-body System Model［J］.Journalof Dynamicsand Control，2012，10（4）：304-323.

［11］WANG Deshi.Dynamics ofmechanical system solved by quadratic programming［M］.New York：Academic Press，1993：63-67.

［12］芮筱亭.有任意个集中质量的转管炮的固有振动［J］.兵工学报，1994（2）：1-5.RUIXiaoting.The natural vibration ofa rotating gun with arbitrary lumped mass［J］.Acta Weapon Industry，1994（2）：1-5.

［13］周起钊.柔性系统力学中的主要课题［J］.力学进展，1989，19（4）：464-476.ZHOUQizhao.Themain topics in themechanics of flexible systems［J］.Advances in Mechanics，1989，19（4）：464-476.

［14］周起钊.多体系统力学的一个重要研究方向［R］.北京：北京大学，1988：1-4.ZHOU Qizhao.An important research direction ofmultibody system dynamics［R］.Beijing：Peking University，1988：1-4.

［15］陆佑方.多柔性体系动力学［M］.北京：科学出版社，1993.124-126.LU Youfang.Flexible Multi-Body System Dynamics［M］.Beijing：Higher Education Press，1993.124-126.

［16］曾攀.有限元分析及应用［M］.北京：清华大学出版社，2003.25-31.ZENG Pan.Finite element analysis and application［M］.Beijing：Tsinghua university press，2003.25-31.