基于超稳定性理论的分数阶MRAC设计

薛长森，戚志东，单 梁，唐鹏亮

(南京理工大学自动化学院，江苏，南京，210094)

0 引 言

对于一些非线性、多变量、强耦合的控制对象，一般的控制方法无法满足高性能控制的需要。研究人员引入MRAC等较为先进的控制算法，并结合模糊控制实现参数实时整定取得了不错的效果[1]。随着工程实际对控制性能要求的进一步提高，学者也尝试将分数阶微积分理论引入到MRAC控制律的设计中。文献[2,3]在基于局部参数最优化律(MIT)设计MRAC时，均采用对目标函数进行分数阶的微分以得到分数阶控制律的方法。前者还给出了具有分数阶参考模型时的MRAC设计方法，仿真实例表明，具有分数阶自适应律的MRAC较整数阶有明显优势；后者也特别定性地分析了参数选定与控制系统稳定性的关系，但这种方法没有从根本上解决控制系统的稳定性问题。文献[4-6]在保证整个控制系统稳定性方面更进一步，他们利用分数阶微积分的知识推广了Lyapunov第二法，并根据分数阶系统的Lyapunov稳定性判据设计了分数阶的自适应控制律，这样不仅提高了MRAC的控制性能，也保证了整体的稳定性，但基于Lyapunov稳定性理论设计的自适应控制器优劣取决于设计者的经验和技巧，且自适应控制律往往含有误差的积分，参数调整缓慢[7]，同样的问题依然存在于分数阶MRAC的设计中，使其在实际应用中有相当的局限性。

本文以分数阶微积分的性质为基础，并结合Po-pov超稳定性理论，提出了一种新的分数阶MRAC设计方法。该方法在保证控制系统稳定的同时，控制律选取灵活，设计过程规范以便于实际应用。同时，以超声波电机的转速控制为仿真实例，结果表明，相比整数阶MRAC，通过选取适当的分数阶积分阶次，分数阶MRAC可提高系统输出的收敛速度，减小超调量，并表现出更优的鲁棒性。

1 分数阶微积分及其数值解法

1.1 分数阶微积分基础

分数阶微积分通用表达式如下[8]：

(1)

在分数阶微积分理论的研究进程中，由整数阶微积分直接推广得到的分数阶微积分定义，其形式有所不同[9]。其中，Riemann-Liouville(RL)定义为：若f(t)在(0,+∞)上逐段连续，并且在[0,+∞)区间上可积，对于t>0,Re(ν)>0，则：

(2)

函数f(t)的ν阶RL积分，其中Γ(ν)为伽马函数：

(3)

1.2 分数阶微积分的数值算法

本文采用Oustaloup滤波器算法作为分数阶微积分的数值求解方法，其实现方式简单且在近似频段内效果良好[10]。具体实现过程如下：

(4)

其中，γ为任意实数。为获得较高的近似精度，在选定的拟合频率段(ωb,ωh)内用一个分数阶传递函数F(s)来近似分数阶微分算子sγ，F(s)如下所示。

(5)

对上式进行一阶泰勒公式展开，可得：

(6)

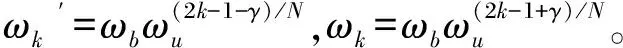
2 基于Popov超稳定性理论的分数阶MRAC设计方法

2.1 Popov超稳定性理论

超稳定性问题是Popov在20世纪60年代对绝对稳定性研究过程中，作为绝对稳定性问题的一个推广而提出的，其理论是MRAC设计的主要理论基础之一[11]。

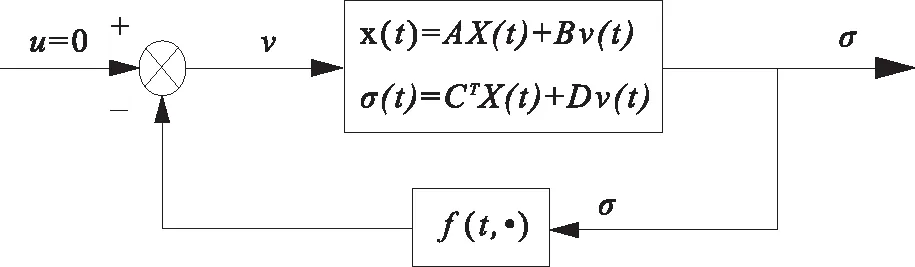
图1 一类非线性控制系统

如图1所示的一类非线性控制系统，系统由一个前向通道和一个反馈通道组成，其前向通道是线性时不变的，而反馈通道一般是非线性时变的，系统描述为

(7)

式中，x∈Rn；ω,v∈Rp；A∈Rn×n；B∈Rn×p；C∈Rp×n；D∈Rp×p；f(t,τ,σ)表示σ→ω的映射，一般为一个泛函。

超稳定性定理 针对式(7)描述的反馈系统，如果反馈通道满足Popov不等式，即有

(8)

其(渐进)超稳定的充要条件是，前向通道的传递函数矩阵是(严格)正实的[12]。

2.2 分数阶MRAC设计方法

若控制系统的状态可测，可利用其状态变量来设计分数阶MRAC。考虑如下自适应控制系统：

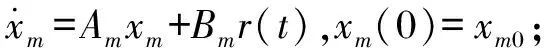
前向通道线性变换量：v=De；

自适应控制参数：

分数阶MRAC系统的设计目标为：寻找D、Φ1(v,t,τ)、Φ2(v,t)、Ψ1(v,t,τ)、Ψ2(v,t)，使得对于任意初始条件(As(0)，Bs(0))、任意初始系统参数(xm(0)，xp(0))和分段连续的输入量r，自适应控制系统是全局渐近稳定，并且自适应参数是收敛的[13]。

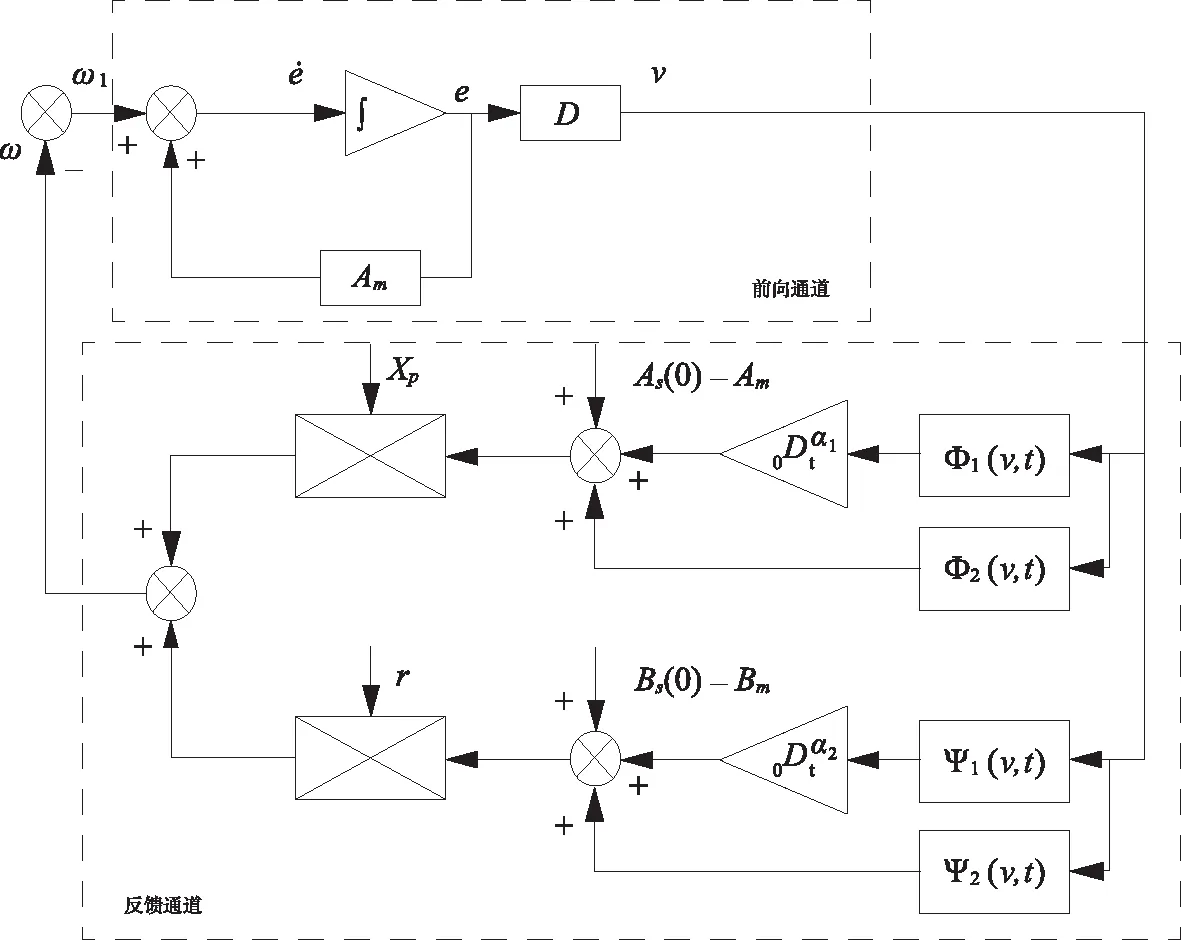
图2 等价反馈系统

基于状态变量的分数阶MRAC设计过程如下：

a) 将原系统描述为一个如图2的等价反馈系统。

其中，前向方框为：

(9)

反馈方框为：

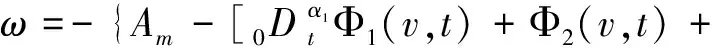
(10)

b) 决定可调参数Φ1(v,t)、Φ2(v,t)、Ψ1(v,t)、Ψ2(v,t)，使反馈通道满足Popov不等式，即：

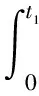
(11)

结合式(10)可得：

η(0,t1)=

(12)

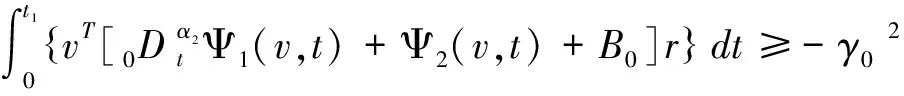
其中，A0=As(0)-Am，B0=Bs(0)-Bm，α1<0，α2<0。可得：

(13)

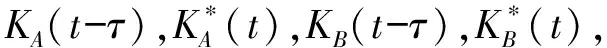
若取Φ1(v,t,τ)=KA(t-τ)v(τ)xT(τ)，则

ηΦ1(0,t1)=

(14)

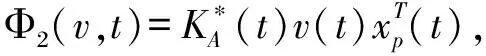
(15)

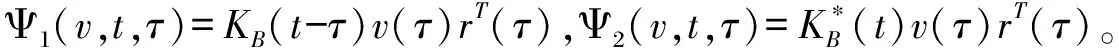
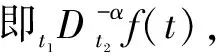
证明 根据Riemann-Liouville(R-L)定义，分数阶积分可表示为

(16)

式(16)中

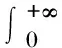
(17)

运用上述性质，在可调参数选取方案不变的情况下，只是将整数阶积分全部替换为分数阶积分，容易得出：

(18)

同理可得：

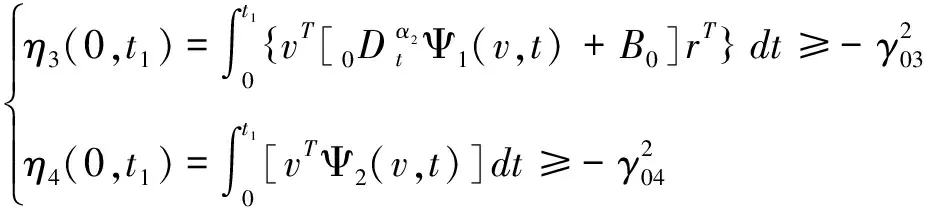
(19)

c) 决定前向方框中D，使得等效反馈系统满足Popov超稳定定理。

为满足前向通道正实性的要求，可取D=P>0使得：

(20)

当参考模型是渐近稳定时，式(20)有唯一解。

3 仿真实例

以文献[14]中建立的ShinseiUSR60型两相行波超声波电机的阶跃响应模型为例。

(s2+632.6935002s+α0)n=βNref

(21)

式中，α0，β为电机运行时受自身或外界干扰时变的参数。

期望的性能指标为：在阶跃信号作用下，电机的转速响应时间在0.3秒内且无超调，故将参考模型[15]设置为：

(s2+632.6935002s+25000)n=25000Nref

(22)

根据分数阶MRAC的设计方法，将α0，β作为控制律中的可调因子，可得：

(23)

a) 启动阶段

图3 不同阶次控制律作用下的电机阶跃响应

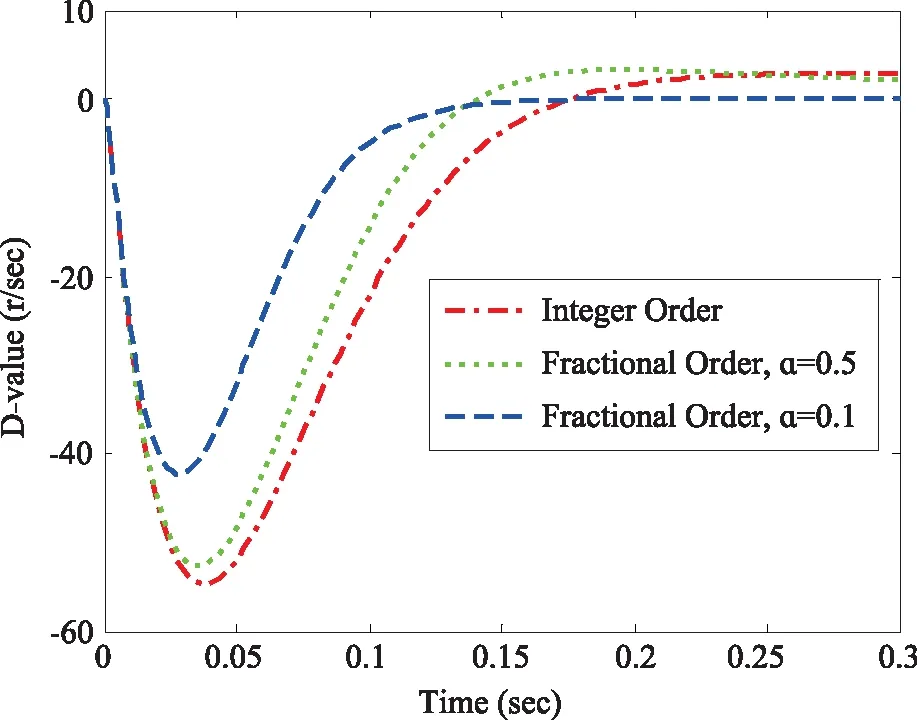
图4 不同阶次控制律作用下的电机阶跃响应差值

在电机启动阶段，设置目标转速为100 r/s的阶跃信号，图3、图4分别为不同阶次控制律作用下的电机阶跃响应曲线以及它们与参考模型的响应误差。从图3中可以看出，理想参考模型的阶跃响应在0.15 s达到稳态值100 r/s，传统的整数阶MRAC可使电机转速在0.25 s达到稳态，图4显示其在0.25～0.3 s内有2 r/s的稳态误差。本文所设计的分数阶MRAC，引入了可调因子——分数阶积分阶次α，从上面两图可以看出，当α减小到0.1时，稳定时间约为0.15 s，且无明显稳态误差。在其他因素一定的情况下，相比传统的整数阶MRAC，通过降低积分阶次可加快电机转速的收敛速度，同时减小稳态误差。

b) 负载突变阶段

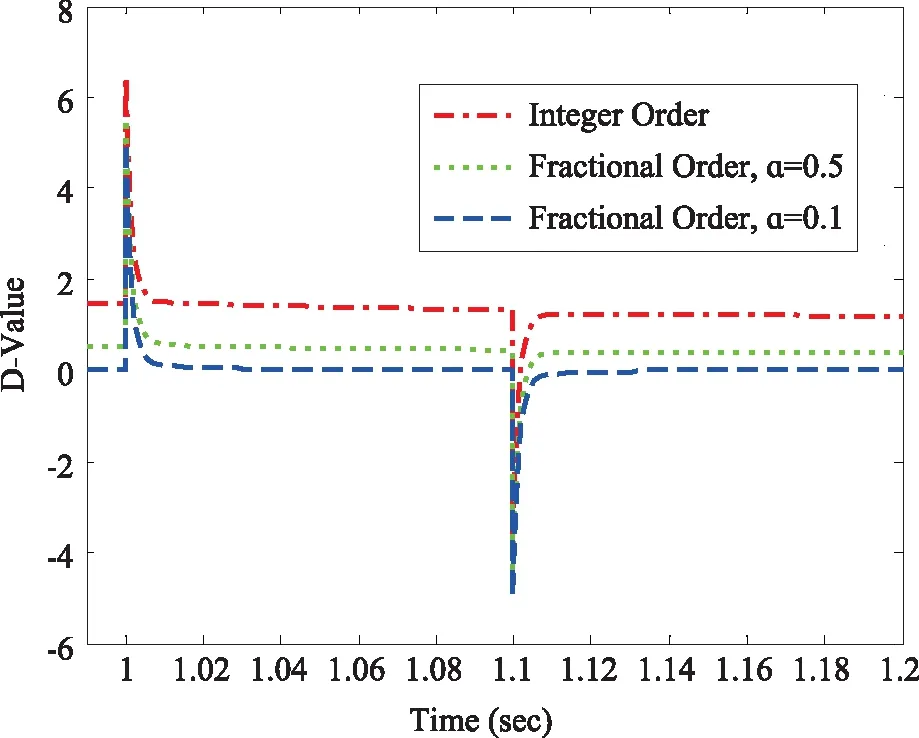
图5 负载变化时的电机响应情况

负载突变可以更好地测试所设计的分数阶控制策略的抗干扰能力，因此在1 s和1.1 s模拟电机负载突变的情况，在原阶跃响应的基础上分别给予±5 r/s 的转速突变。如图5所示，由于整数阶MRAC和α=0.5时的分数阶MRAC在之前时刻与参考模型的输出存在明显误差，但设计方法决定了随着时间的积累，误差终要归零，这就使得在1～1.2 s内，它们的响应误差曲线整体渐近于零，并且出现转速突变大于5 r/s现象。同时，随着积分阶次的下降，电机的转速能更加快速的稳定在期望的目标，表现出更加良好的鲁棒性。

4 结束语

本文基于Popov超稳定性理论和分数阶知识，提出了一种分数阶MRAC的设计方法，从设计过程来看，该分数阶MRAC在满足整体系统(渐近)超稳定的同时，设计流程更加规范以便于工程时间人员的掌握，控制策略的选择也更加灵活，相比基于MIT法和Lyapunov第二法的分数阶MRAC设计具有明显优势；另一方面，分数阶MRAC相对于传统的整数阶MRAC，每一个可调参数都引入了可调因子——分数阶积分阶次，通过两相行波超声波电机的仿真实例可以看出，通过降低分数阶积分阶次，可以提高控制对象的响应速度，降低稳态误差并提高系统的鲁棒性，与整数阶MRAC相比优势明显。

[1] 李晓庆,高春能,纪志成. 基于MRFAC的感应电机控制器设计[J]. 南京理工大学学报(自然科学版), 2005 (S1): 91-95.

Li Xiaoqing, Gao Chunneng, Ji Zhicheng. Design of Speed Controller of Induction Motor Based on MRFAC [J]. Journal of Nanjing University of Science and Technology, 2005 (S1): 91-95.

[2] Vinagre B M, Petráš I, Podlubny I, et al. Using Fractional Order Adjustment Rules and Fractional Order Reference Models in Model-Reference Adaptive Control [J]. Nonlinear Dynamics, 2002, 29(1): 269-279.

[3] 陈宁,陈南,王乃洲.基于分数阶参考模型的车辆悬架自适应控制[J].南京林业大学学报自然科学版, 2009, 33(3): 116-120.

Chen Ning, Chen Nan, Wang Naizhou. Adaptive Control of Vehicle Suspension using Fractional Order Reference Models [J].Natural Science Journal of Nanjing Forestry University, 2009, 33 (3):116-120.

[4] Takamatsu T, Ohmori H. Design of Model Reference Adaptive Control Systems with Fractional Order Adaptive Law and Its Lyapunov Stability [A]. Chinese Control Conference[C]. Piscataway, NJ: IEEE, 2014: 8853-8858.

[5] 白珍龙.分数阶模型参考自适应控制的研究及其在重碱煅烧中的应用[D].山东: 青岛科技大学, 2008.

Bai Zhenlong.Research on Fractional Order Model Reference Adaptive Control Systems and Its application To Heave Soda Steam Calcaneal on Process [D]. Shandong: Qingdao University of Science & Technology, 2008.

[6] 刘思铭. 分数阶模型参考自适应控制研究[D].黑龙江:黑龙江大学,2012.

Liu Siming. Fractional Model Reference Adaptive Control [D]. Heilongjiang: Heilongjiang University, 2012.

[7] 韩正之，陈彭年，陈树中.自适应控制[M].北京:清华大学出版社,2011:37-40.

Han Zhengzhi, Chen Pengnian, Chen Shuzhong.Adaptive Control [M]. Beijing: Tsinghua University press, 2011:37-40.

[8] 李远禄. 分数阶微积分滤波原理、应用及分数阶系统辨识[D].南京航空航天大学,2007.

Li Yuanlu.Principle and Application of Fractional Calculus Filter and Fractional Order System Identification [D]. Nanjing University of Aeronautics & Astronautics, 2007.

[9] 薛定宇,陈阳泉.高等应用数学问题的MATLAB求解[M]. 北京:清华大学出版社,2013:437-440.

Xue Dingyu,Chen Yangquan. The MATLAB solution of higher applied mathematics [M]. Beijing: Tsinghua University press, 2013:437-440.

[10] 白珍龙. 分数阶模型参考自适应控制的Matlab设计[J].工业仪表与自动化装置,2016(1):30-34.

Bai Zhenlong. Design of Fractional Order Model Reference Adaptive Control by Matlab [J].Industrial Instrumentation and Automation, 2016 (1): 30-34.

[11] 柴天佑,岳恒. 自适应控制[M]. 北京: 清华大学出版社, 2016: 150.

Tianyou Chai, Yue Heng.Adaptive control [M]. Beijing: Tsinghua University press, 2016:150.

[12] 刘小河,管萍,刘丽华.自适应控制理论及应用[M].北京: 科学出版社,2011:9-13.

Liu Xiaohe, Guan Ping, Liu Lihua.Adaptive Control Theory and Application [M]. Beijing: Science Press, 2011:9-13.

[13] 徐国凯,赵秀春,宋鹏.一种简化的多变量MRAC系统设计[J].大连民族学院学报,2006,8(3):1-4.

Xu Guokai, Zhao Xiuchun, Song Peng. A Simplified Multivariable MRAC System Design [J].Journal of Dalian Nationalities University, 2006,8 (3): 1-4.

[14] 史敬灼.超声波电机运动控制理论与技术[M].北京: 科学出版社, 2011:29-85.

Shi Jing.Ultrasonic Motor Motion Control Theory and Technology [M]. Beijing: Science Press, 2011:29-85.

[15] 沈晓茜. 基于波波夫超稳定理论的超声波电机MRAC控制研究[D]. 河南: 河南科技大学, 2014.

Shen Xiaoqian.Study on MRAC Control Of Ultrasonic Motor Based On The Theory Of Super Stability [D]. Henan: Henan University of Science and Technology, 2014.