针对复合材料无人机的激光武器系统杀伤效能仿真计算

王 喆，许凌飞，顾村锋

(上海机电工程研究所，上海,201109)

0 引 言

目前，“低慢小”类飞行器已逐渐由一种边缘武器类型变为人们关注的焦点。这类目标具有低空、慢速、小型等特点，飞行高度在1000米以下，飞行时速小于200公里、雷达反射面积小于2平方米，典型飞行器包括各类小型固定翼和旋翼无人机。随着“低慢小”类飞行器应用的普及、技术的发展，其对公共安全和国土防空都构成了潜在的威胁。

针对该小型无人机的威胁，拟采用小型化高功率固体激光技术，通过高精度的跟瞄设备，利用强激光武器对该类目标进行打击。强激光定向能武器采用高能激光器产生激光束，通过光学系统将攻击目标的激光束聚焦在攻击点上，使光能量在目标上的有效沉积，对目标实施精确杀伤。强激光定向能武器对目标的杀伤方式主要分为硬杀伤和软杀伤，硬杀伤是使目标材料受热软化、熔融、穿孔(热烧蚀)，可实现引爆战斗部、发动机，破坏气动外形等，从而摧毁目标；软杀伤是指破坏或干扰目标传感器，从而使目标无法正常工作。

激光的毁伤过程是将激光光束聚焦在目标的表面上，产生足够强的光功率密度，通过光与物质的相互作用机理，在目标上产生热效应、力效应，从而达到对目标的损伤，而这里的损伤并非是真正意义上的“毁伤效果”，只有通过对目标关键点的分析，对其关键点进行损伤，才能达到武器应用中的毁伤效果。

激光是利用光、热、电、化学能或原子核等外部能量，激励物质使其受激辐射而产生的一种特殊的光[1-3]。同一般光源所发出的光相比，激光更有许多优异的物理特性。如果把高能激光聚焦成束，能产生数百万到数千万度的高温、数千万大气压的高压、数千万伏/平方厘米的强电场，以用来摧毁敌方的装甲兵器和引爆炸弹等[4,5]。激光武器则是以产生强激光束的激光器为核心，加上瞄准跟踪系统和光束控制与发射系统组成的高技术武器，它可利用激光的能量直接摧毁对方的目标或使对方丧失战斗能力[6]。

激光系统设计需要对系统进行初步的性能估算，性能估算来源于对系统需求的详细分析，这些要求将指导设计的完成[7]。

本文建立了描述激光毁伤能力的理论模型并进行相关计算。通过像差衍射理论模型及大气统计光传输模型，建立了激光武器系统中的发射望远镜及大气传输造成的光束质量恶化模型，结合跟瞄系统的跟踪精度给出了在靶面上的光斑强度分布。同时，通过试验确定了材料的基本毁伤阈值，从而建立一套相应的激光毁伤指标体系并提供激光武器系统杀伤区范围估算。

目前，激光武器作为近程末端防御系统之一，具有十分良好的发展前景。本文从激光输出功率及光束质量两方面考虑，结合空间中光束自衍射效应及大气湍流效应的影响，计算得到了到靶光功率密度分布图像，对今后激光武器的发展具有十分重要的参考价值。

1 激光传输链路理论分析

激光从出射端开始，通过发射望远镜聚焦至目标表面所受到的影响主要由两大部分组成：跟瞄光学跟踪系统及大气环境。对光场的影响可以从两个角度来进行分析：(1)对于光场总能量的影响，主要的因素在于发射望远镜系统总体的光学效率(光学元器件的透过率、反射率等)及大气的透过率(气溶胶等因素)；(2)对光场波前分布的影响，光场波前的分布将对聚焦点处的光场强度(功率密度)分布，即光斑的大小，形状等参数产生作用，其主要因素在于跟瞄系统发射望远镜的像差，跟瞄系统的离焦误差，跟瞄系统的跟踪精度以及大气折射率分布的不均匀性。

1.1 跟瞄系统模型

光学系统必然带有一定的像差，造成光斑的扩展，对于光学聚焦系统，在跟瞄设计中需要保证主激光与发射望远镜光轴的同轴性，这直接导致发射望远镜视场较小。因此针对该系统，其像差主要由球差组成，其余因素(如慧差)等可忽略不计。

跟瞄的跟踪精度产生的影响是指光束在目标表面上的会聚光斑按照一定的分布在晃动，这种扰动对于光场效果来说，是一种扩展，对光斑的会聚效果进行影响。

1.1.1 跟瞄光学系统理论模型(像差的衍射理论)

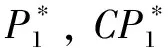
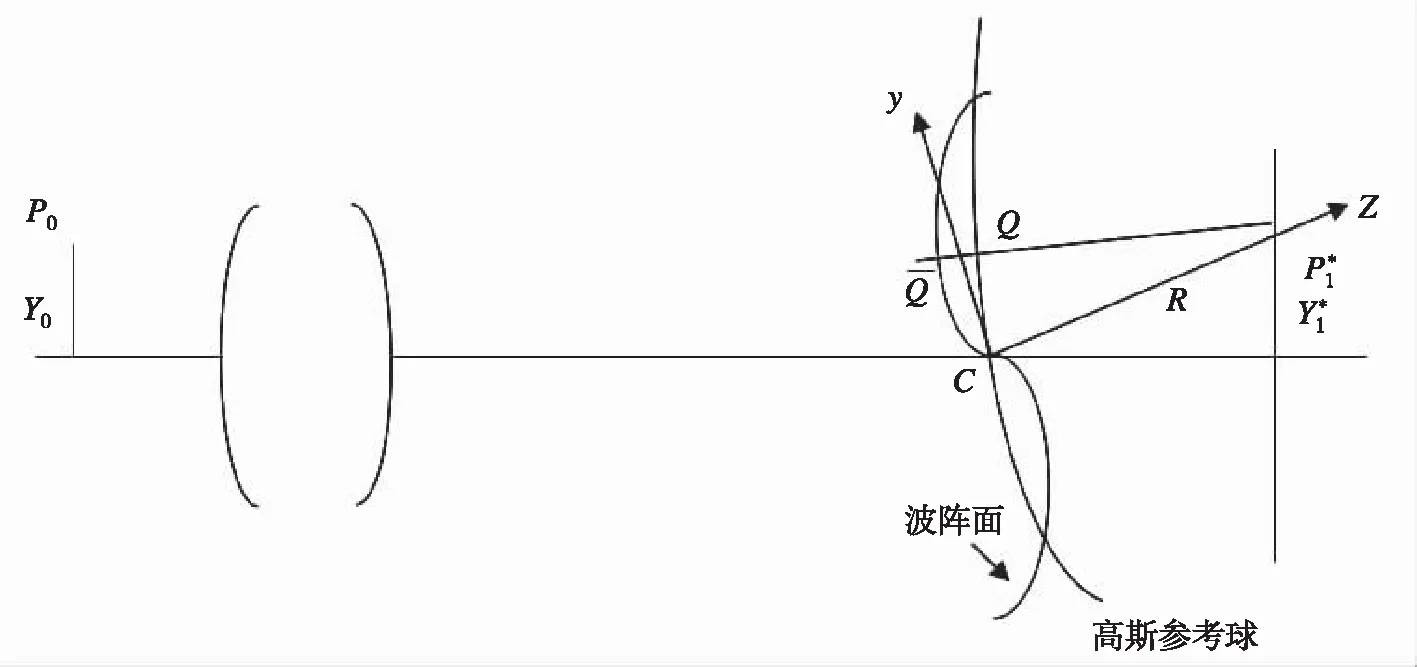
图1 参考系示意图

设高斯参考球的半径为R，s是Q和像区中任意一点P的距离。Q点处的场扰动用Aeik(Φ-R)/R表示，其中A/R是Q点处的振幅。

忽略参考球上倾斜因子的变化，假设波阵面上各点的振幅基本不变[9]。设Q(ξ,η,ζ),P(x,y,z)，出射光瞳半径为a。令

ξ=aρsinθ,x=rsinψ,

η=aρcosθ,y=rcosψ,

(1)

将其转换为“光学坐标u和v”，并且有：

(2)

(3)

高斯参考球面元dS=a2ρdρdθ，积分范围取0≤ρ≤1,0≤θ<2π，可以得到P点的扰动[10]为：

(4)

所以P点的强度为

(5)

1.1.2 跟瞄系统跟踪精度

跟瞄系统在锁定目标打击点位时，有一定的误差，这种误差将会影响到激光毁伤的效率。跟瞄系统的跟踪精度可以用误差概率分布的形式来表述，通过数学模型的建立，这种误差分布与激光光斑之间存在着一种天然的卷积联系，由此，跟瞄系统的跟踪精度影响可以作为一种附加的传递函数，在光传输链路上实现。

假设跟瞄系统的跟踪精度概率密度为f(r)，在打击过程中，光束指向的漂移量与光斑的关系如图2所示：

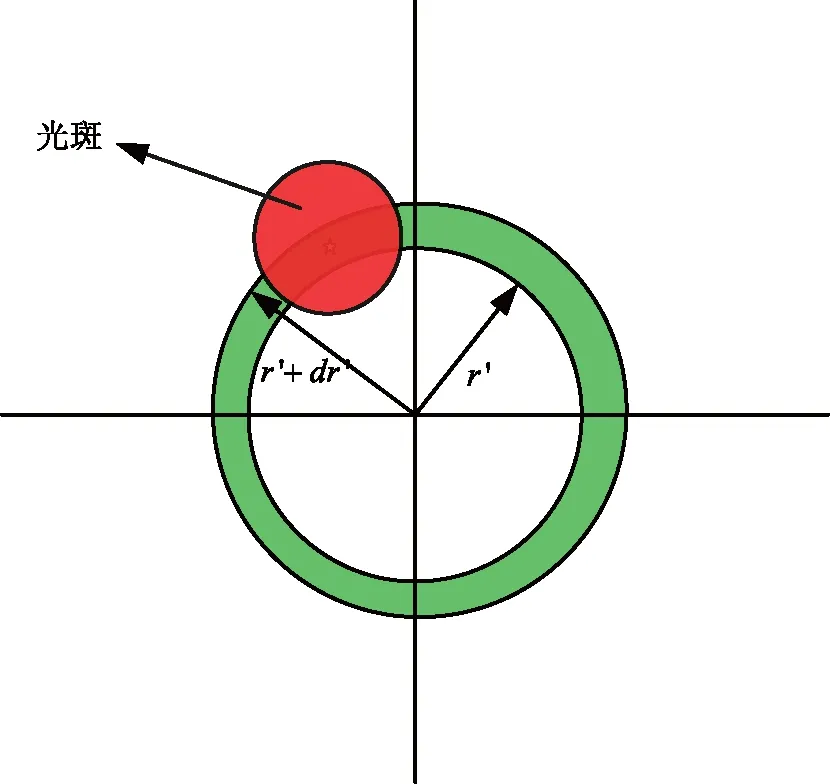
图2 跟瞄精度误差对光斑的影响

假设在时间t内，有N个光子到达靶面，因为跟瞄精度误差分布为f(r)，那么光束指向在图中绿色环中的，到达的光子数为Nf(r′)dr′。而对于单个光子，光场的强度分布可以有上节的光场分布得到，那么，在环中的光场强度分布则可以表示为：I(r-r′)。由此，很容易得到，在一定的打击时间内，在跟瞄影响下，光场的分布为：

(6)

上式描述了另一个事实：跟瞄系统的跟踪精度概率分布可以以传递函数的形式在光传输链路上体现。其传递函数的形式就是跟踪精度概率密度函数的傅立叶变换。

1.2 大气模型

激光光束经过跟瞄系统的发射望远镜到目标之间的传输过程是在稠密大气层中进行的，这段传输过程其本质上是一个复杂的过程。

首先，由于大气中的吸收，气溶胶的散射，影响到了激光的功率，在激光传输过程中，其总功率受到这些因素的影响产生了一定的衰减；其次，大气中由于气流的流动，介质场是一种密度非均匀的介质，导致了大气中的折射率会有一定的起伏，或说是湍流状况。由于湍流的存在，激光在大气中的传输不能够由自由空间的衍射方程来描述，其实质上是一种弱散射的过程。这种影响不仅仅是对激光光场波前的影响，而且也会对激光振幅项产生足够的影响，从而导致了激光漂移、闪烁、破碎等大气/气动光学的现象。大气传输段对与激光的影响是剧烈的，且对毁伤效能的影响有时是致命的。

1.2.1 大气透过率

大气中的分子吸收、水汽吸收及气溶胶的吸收和后向散射都会对激光的传输功率造成影响，如同跟瞄光学系统中的镜面反射率、透射率等参数一样，仅仅对激光的功率产生一个等比线性衰减。这种等比线性的衰减因子与大气中的具体成分相关，在不同的传输路径中，大气的成分是不一样的，因此，整个大气的透过率是随着传输距离和传输角度的不同而不同的。

从目前的状况来说，对于大气衰减(在大气光学中又称为气溶胶传函)可以利用MORTRAN3.0计算得到。对海洋大气环境下的透过率状态进行了计算，距离从1 km到10 km，计算间隔0.5 km，仰角从0°(平视)到85°，间隔5°，由此可以得到一组大气透过率的插值表格，在具体的分析中，使用该表格插值可以得到任意仰角和距离下的大气透过率，如图3所示。

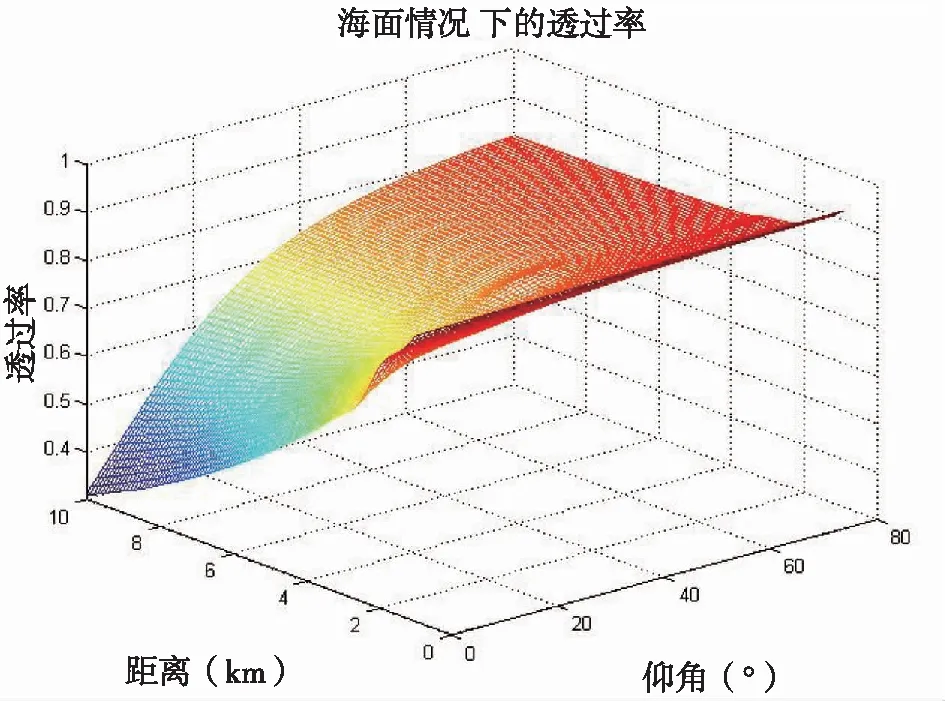
图3 海洋环境下的大气透过率(MORTRAN3.0计算)

可以看到，大气透过率都随着仰角的不同而不同。在低仰角情况下，大气透过率随距离的衰减较大，而在高仰角情况下，大气透过率随着距离的变化较小。

1.2.2 大气湍流模型

根据前苏联科学家柯尔莫哥洛夫的研究理论，他将功率谱密度描述分为三个区，即输入区、惯性子区、耗散区，如图4所示。对于很小的κ=2π/L0，此时湍流尺寸很大，我们将这个区域描述为输入区，在这个区内特定的湍流产生的过程决定了功率谱的形状样式，空间功率谱通常是各向异性的；对于很大的κ=2π/l0，此时湍流尺寸很小，我们将这个区域描述为耗散区；在输入区和耗散区之间的区域我们将其描述为惯性子区，空间功率谱只有在惯性子区以及耗散区这两个区域具有各向同性的特点。

图4 射功率谱范围

从光束传输的理论角度上来说，影响折射率起伏的重要因素是温度起伏，功率谱密度的函数形式和温度起伏、速度起伏的功率谱具有相同的形式，并满足著名的柯尔莫哥洛夫功率谱定律。

(7)

在随机介质中，光与介质相互作用会散射衰减，一般主要的有两种方式来表述散射效应，一是波恩近似，二是Rytov近似。在研究大气传输时，由于湍流的作用，一般采用Rytov近似来描述随机介质中的光的散射场。

在Rytov近似中，通过随机介质的光场复振幅可以表述为：

U(r,L)=U0(r,L)exp[ψ(r,L)]

(8)

其中，U0(r,L)表示光在自由空间中的复振幅，指数项中的函数可以展开为：

ψ(r,L)=ψ1(r,L)+ψ2(r,L)+……

(9)

对于折射率介质，可以认为：

n(R)=n0+n1(R)

(10)

这里将随机介质看成一个宽平稳过程，即可以引入介质的功率谱函数：

n1(s,z)=∬exp(iK·s)dν(K,z)

(11)

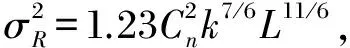
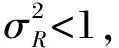
在球面波形式下，光学系统的点扩散函数可以表示为[11]：

(12)

综上，激光的到靶功率密度的空间分布可以表示为大气传函与光学系统传函的乘积。即：

(13)

2 复合材料毁伤阈值测定

本文中，主要展开了对材料本身击穿毁伤的研究工作。对于毁伤而言，另一项重要的参数是针对不同的材料特性，确定对目标的毁伤时间及在规定毁伤时间内的毁伤阈值。这种特性参数是通过试验来确定的。本文中所研究的材料是一般小型无人机所常用的工程塑料复合材料。此类材料热导率低，阻燃，一般涂抹白漆的情况下会在照射处使得大部分能量被漫反射。对于此类材料的击穿毁伤以热烧蚀为主要毁伤方式，通过材料对激光能量的吸收，产生热积累，逐渐烧蚀。

实验采用2 000 W-400 Hz-200 μs-占空比8%的重频激光照射目标材料，记录激光辐射时间以及目标表面温度，观察不同激光功率密度条件下，对材料的毁伤效果。实验原理图如图5所示。

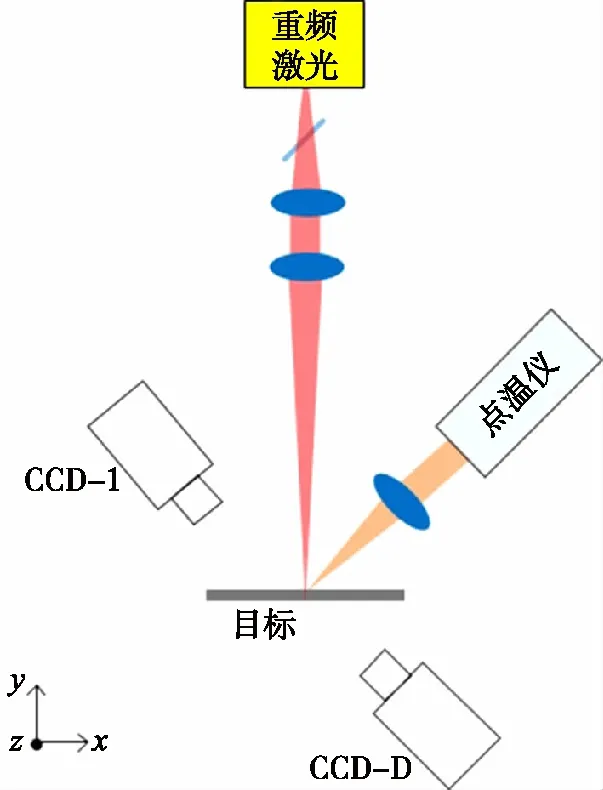
图5 实验原理图

编号1～4分别对应重频318 W/cm2激光辐照时间5 s,1 s,2 s,3 s的结果，编号5为480 W连续激光辐照1 s结果。其前后表面毁伤效果实物图如图6所示。

a) 无人机外壳前表面毁伤形貌图

b) 无人机外壳后表面毁伤形貌图图6 无人机外壳前后表面毁伤图

通过调整试验用激光功率及光斑大小，可以控制激光的到靶功率密度。由此，可以得到在不同时间下，无人机材料的烧穿阈值如图所示：

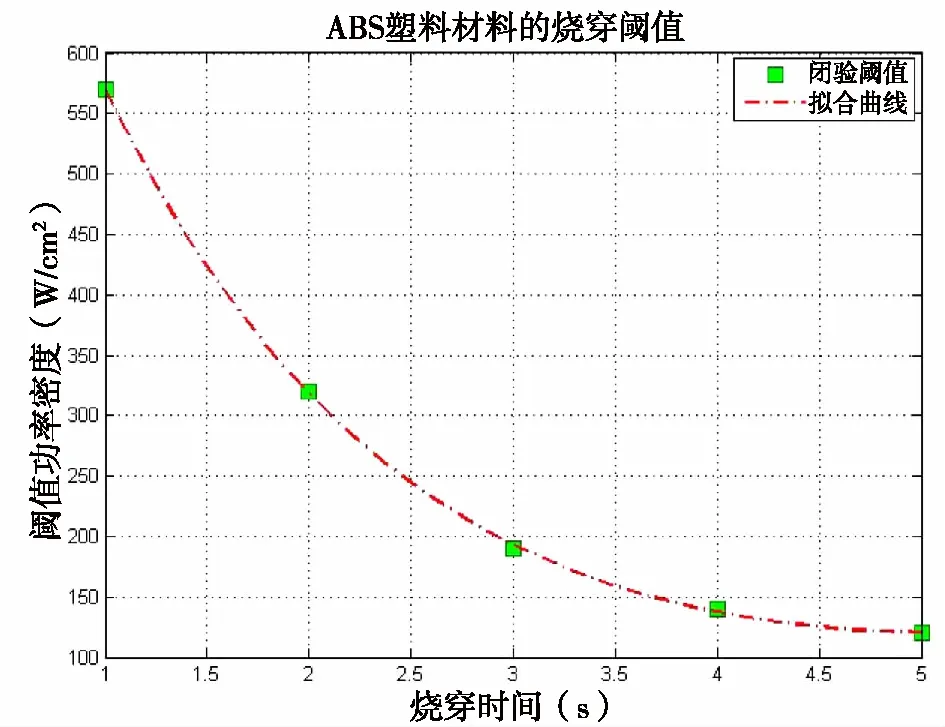
图7 不同时间的ABS材料的烧穿阈值

3 激光武器系统毁伤效能仿真分析

计算参数选择：平均功率100 kw及200 kw，占空比8%，光束质量β值5(等效于光斑口径的损失)，放大率1∶2.2。激光器采用非稳腔设计，出射的脉冲光为平行平面波，并非传统意义上的高斯光束。

以320 W/cm2作为毁伤功率密度阈值，考虑了大气因素，跟瞄因素等参数对光束聚焦性能的影响，在不同仰角下，激光毁伤杀伤区如图8所示。

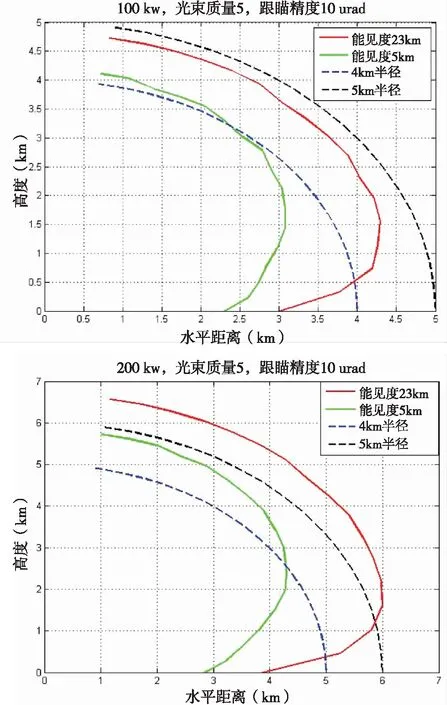
图8 激光杀伤区

图8给出了不同能见度情况下的激光杀伤区范围。激光器功率选择了100 kW及200 kW的激光功率。绿色曲线表示5 km的能见度，红色曲线表示23 km的能见度。

从图8中可以看到，激光毁伤的有效区域随着仰角的不同而不同，仰角越大，有效毁伤区域也就越远。其原因在于大气透过率与大气相干长度。而大气相干长度是主导的因素，随着仰角的提升，大气相干长度增加，更有利于激光能量的聚焦，使其到靶功率密度能够达到无人机的毁伤阈值。而大气透过率的作用，通过图8可以看到，在高功率情况下，低仰角比较明显，随着仰角的升高，能见度的影响越来越小。

4 结束语

本文主要研究了激光的毁伤计算模型，主要讨论了针对无人机外壳材料的到靶光斑图、能量密度分布及最大毁伤距离。考虑只含有单种球差的衍射理论，采用Lommel三维衍射积分，计算得到含有离焦像差，以及大气传输所带来的光斑展宽效应的光斑图像及能量密度。通过计算，给出了100 kW激光武器系统及200 kW 激光武器系统对于无人机的杀伤范围，随着射击仰角的变化，杀伤距离起伏较大。

[1] 李传胪.新概念武器[M].北京：国防工业出版社，1999.

[2] 周义，周丽，胡根秀，等.未来战争主攻手——美军激光武器即将走向战场[J].飞航导弹，2005，(10)：32-36.

[3] 余宗敏，蔡传能.未来战场的攻防新锐——激光武器[J].飞航导弹，2005，(2)：62-64.

[4] 陆彦文，陆启生.军用激光技术[M].北京：国防工业出版社，1999.

[5] 宛东生.关注美国机载激光武器(ABL)计划[J].激光与光电子学进展，2006，43(3)：28-31.

[6] 李楠，何友金.舰载激光武器浅谈[J].光电技术应用，2005，20(3)：11-13.

[7] 赵书文，周世明，尤志锋.未来防空与防天利器——飞速发展的激光武器[J].飞航导弹，2005，(8)：1-3.

[9] R. Courant, D. Hilbert, Methods of Mathematical Physics[J] , Vol.I. 1953.

[10] Emil Wolf, Principles of Optics[J]. Electromagnetic Theory of Propagation, Interference and Diffraction of Light, Seventh Edition. Publishing House of Electronics Industry.2009.10:430-443.

[11] Larry C. Andrews, Ronald L. Phillips. Laser Beam Propagation through Random Media[J].2005:434-436.