基于IMM_UKF的自抗扰控制导引律研究

殷 玮，祁文治

(上海机电工程研究所，上海,201109)

0 引 言

现代战争对抗形式复杂多变，随着电磁干扰、光电干扰、隐身技术的迅猛发展，采用红外或雷达体制的被动制导导弹由于其隐蔽性好的优点成为主动制导导弹的有效补充，得到广泛的应用。但是它们只能提供导引头测得的视线角，缺少弹目相对距离和速度以及目标加速度。为了使导弹能够应对机动形式越来越复杂的攻击目标，需要在准确估计目标运动信息后，设计能快速响应目标机动且鲁棒性强的新型制导律以适应现代空战的需求。

为了解决仅有角度制导的被动制导问题，通常采用滤波器与制导律一体化设计的方法。首先利用目标机动建模和滤波跟踪算法进行被动定位[1]，然后通过制导律设计，在改善滤波器跟踪效果的同时，提高导弹的制导精度。在滤波算法方面，交互多模型跟踪算法(IMM)利用多个运动模型分别匹配目标的不同运动状态，输出结果为各模型跟踪结果的加权平均，优于单模型跟踪[2]。无迹卡尔曼滤波算法(UKF)对非线性概率密度分布进行近似，在强非线性时优于常用的扩展卡尔曼滤波(EKF)[3]。在导引律设计方面，滑模变结构理论具有抗干扰和抗参数摄动的特点，能克服滤波算法带来的估计误差，但容易引起弹体的抖振[4]。自抗扰控制器不依赖系统模型，对存在扰动不确定的系统具有良好的控制性能。

本文针对在研被动制导导弹无法获取弹目相对运动信息的制导难点，将交互多模型与无迹卡尔曼滤波算法结合起来，作为目标状态估计算法，同时，采用自抗扰控制方法进行滤波器和导引律的一体化设计，提高系统可观测性，减小滤波算法估计误差，有效提高导弹的作战效能。

1 导弹目标相对运动模型描述

在直角坐标系下，建立目标和导弹的相对运动状态方程。相对运动的描述如图1所示。其中R为弹目相对距离，qε为视线高低角，qβ为视线方位角。

图1 弹目相对运动描述

定义x方向目标相对于导弹的状态矢量为：

(1)

式中目标运动参数通过目标机动模型获得；导弹运动参数通过惯导测量信息及捷联解算算法获得。本文选取Singer模型和“当前”统计模型建立目标运动方程。Singer模型是假设目标加速度为零均值的一阶时间相关模型，概率密度函数近似服从均匀分布，符合目标机动加速度突变时的运动规律；“当前”统计模型假设目标加速度均值为“当前”加速度，概率密度函数服从修正瑞利分布，更适合目标机动加速度连续的情况。

扩展到地面的三个维度后即可求得目标相对导弹的运动状态方程为：

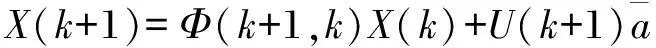
(2)

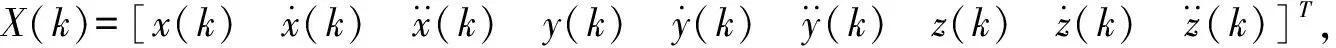
Φ(k+1,k)=diag{φφφ}，

U(k+1,k)=diag{uuu}，u=

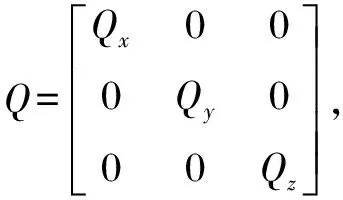
其中，α为机动频率；

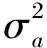
被动导引头观测模型为：

Z(k)=h(k,X(k))+V(k)

(3)

其中:

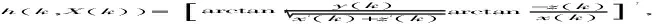
式中：qε(k)和qβ(k)为导引头实际输出测量角，V(k)为测量噪声，E[V(k)]=rI=O2×1，并且满足

vε(k)和vβ(k)相互独立。

2 基于交互多模型的无迹卡尔曼滤波算法(IMM_UKF)

交互多模型算法采用多个卡尔曼滤波器并行处理，每个滤波器对应不同的描述目标运动的状态空间模型，该算法对不同的估计赋予不同的权重，使用各滤波器概率和输出值加权计算得到综合输出值，最终得到最优估值。无迹卡尔曼滤波算法直接使用系统的非线性模型，基于无迹变换采用线性卡尔曼滤波框架，用采样粒子逼近非线性分布，该算法得到的均值和协方差能够精确到二阶。

IMM_UKF的具体算法如下：

a) 对估计的混合：

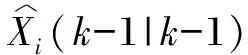
∀i,j∈M，混合概率为：

(4)

(5)

b) 滤波：

(a) 滤波初始化

(6)

σ采样点ξi|j(k+1|k)

新兴电影叙事类型，是相比此前较为多见的传统叙事类型而言的，进入2000年之后才出现的电影叙事类型。2000以来，随着“文化产业”这一概念的提出，“市场”越来越多的受到电影人以及电影相关行业的关注，电影的生产链愈来愈明确的被看做是一种商业行为，而电影的商品化属性也前所未有的被强化，为了迎合受众需求，满足市场要求，继而实现电影产业的利润最大化，粉丝当道的“IP电影”叙事类型应运而生。

(7)

滤波系统的一步预测值

ξi|j(k+1|k)=hj(k,ξi|j(k+1|k))(i=0,1,2,…2n)

(8)

(9)

(10)

(11)

(c) 利用量测信息进行更新

(12)

(13)

(14)

其中，λ=α2(n+κ)-n,本文取α=0.1,κ=0。

c) 模型概率更新：

采用似然函数来更新模型概率μi(k)；

(15)

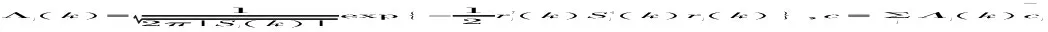
d) 对估计的合并：

∀j∈M

(16)

(17)

图2为IMM_UKF算法的结构框图。

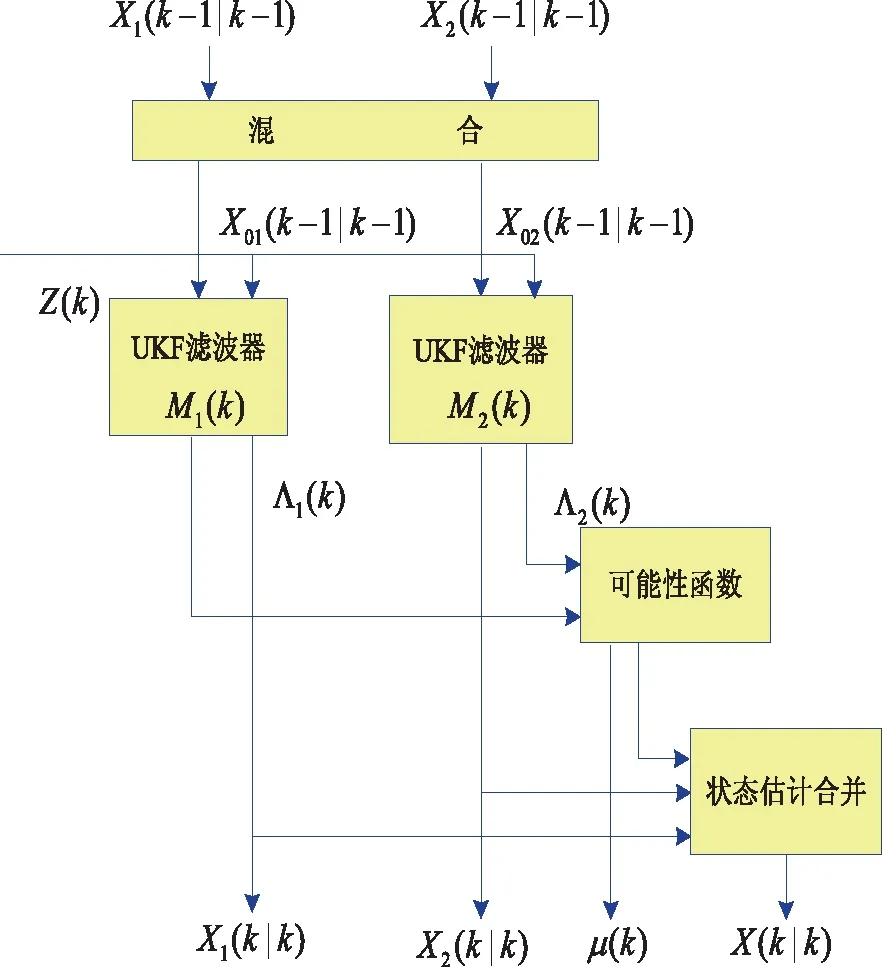
图2 IMM_UKF算法结构框图

3 基于自抗扰控制方法的制导律设计

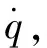
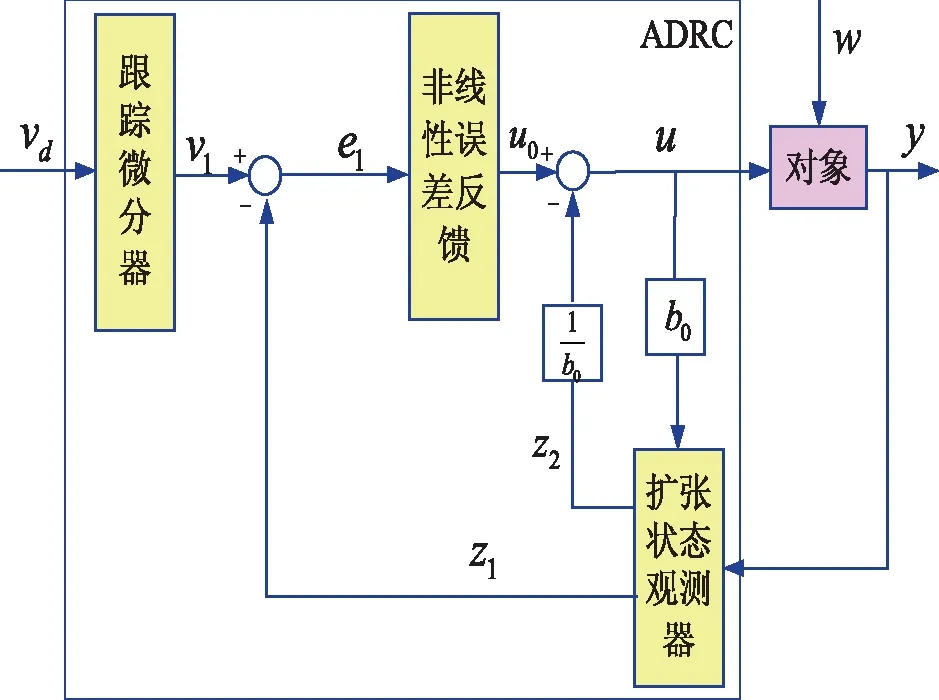
图3 自抗扰控制器

将导弹过载的动态响应特性建模为二阶环节，则其数学描述可以写为：

(18)

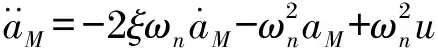
考虑二维平面上的弹-目相对运动方程组：

(19)

则得到整个被控对象为：

(20)

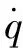
对被控系统设计如下形式的扩张状态观测器：

(21)

β01=10,β02=10。

控制目标为过渡过程与观测器输出差值为零，即z1-v1→0，使用经验函数fal(x,a,δ)设计控制器形式如下：

u0=-β03fal(z1-v1,a03,h03)

(22)

其中β03=0.4,α03=0.5,h03=0.1。

对系统状态方程与扰动进行补偿，取b0=1，则u=u0-z2，形成最终控制量制导指令aMc为：

(23)

4 导弹制导建模与仿真

以某型导弹为例，建立制导控制系统模型，图4为导弹制导控制系统原理图。

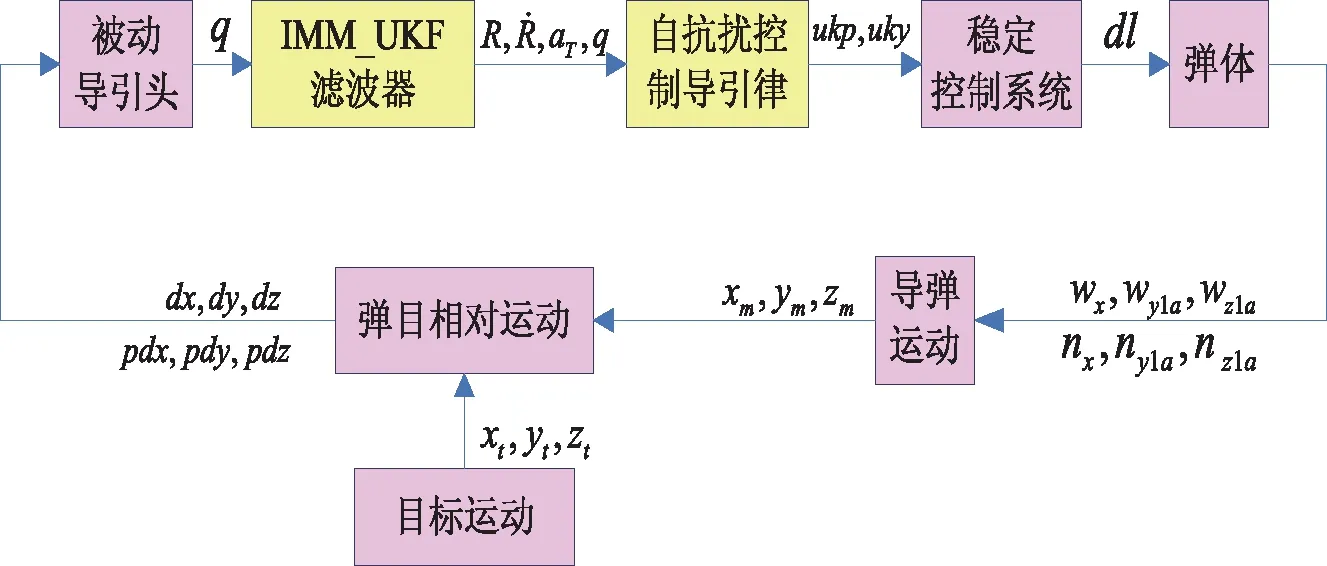
图4 导弹制导控制系统原理图

本文选取两条典型弹道对单模型UKF算法和IMM_UKF算法及修正比例导引和自抗扰控制导引两种方法进行对比仿真。其中序号1是末端大机动逃逸弹道，序号2是全程机动逃逸弹道，初始参数见表1。

表1 弹道初始参数

其中，弹道1仿真结果曲线如图5～图8所示。图5为采用单模型UKF算法和IMM_UKF算法估计得到目标机动和弹目相对速度和距离与真实值对比情况。图6为IMM_UKF算法的模型概率曲线。图7和图8分别为采用修正比例导引和自抗扰控制导引的过载响应以及弹目运动空间轨迹曲线。

图5(a) 垂直于视线方向目标过载

图5(b) 弹目相对速度和距离

图6 IMM_UKF模型概率曲线

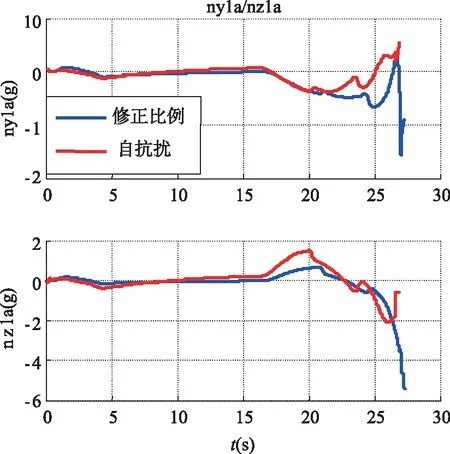
图7 过载响应曲线

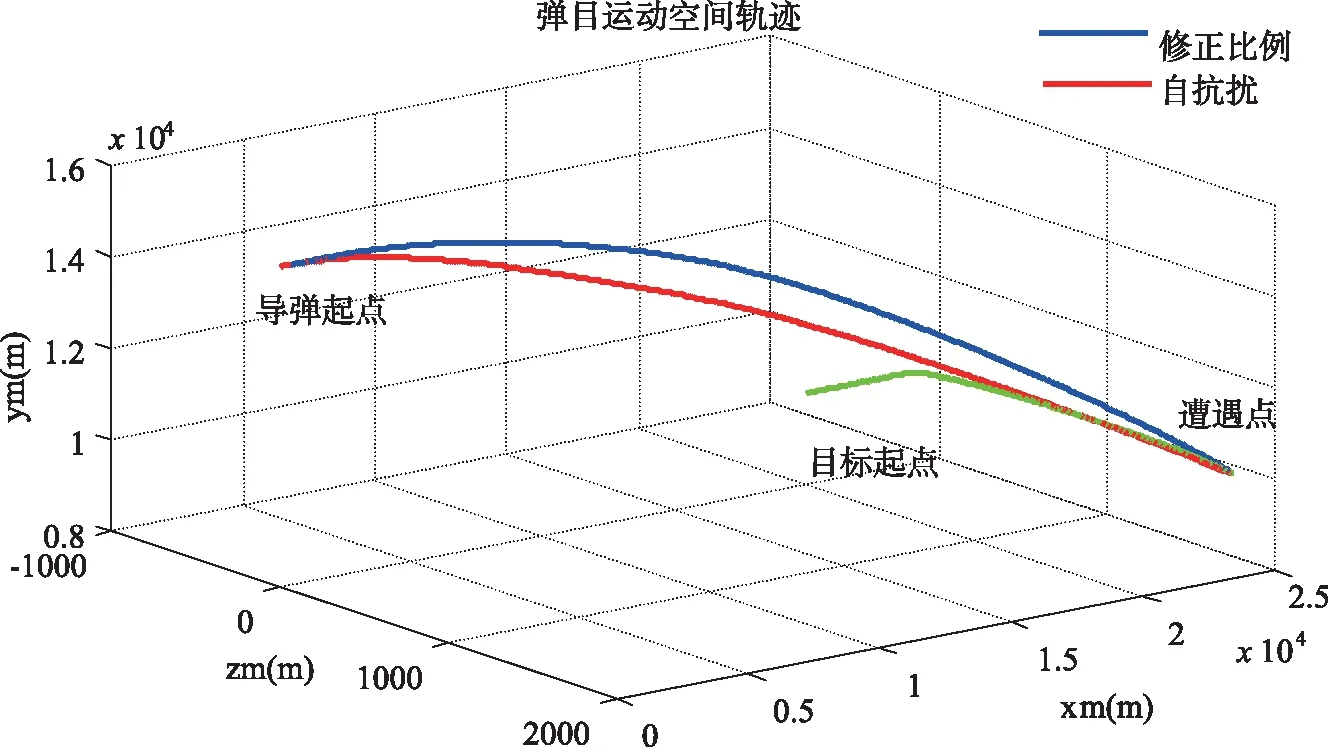
图8 弹目运动空间轨迹

经过100次蒙特卡洛仿真得到的脱靶量统计情况如表2所示。

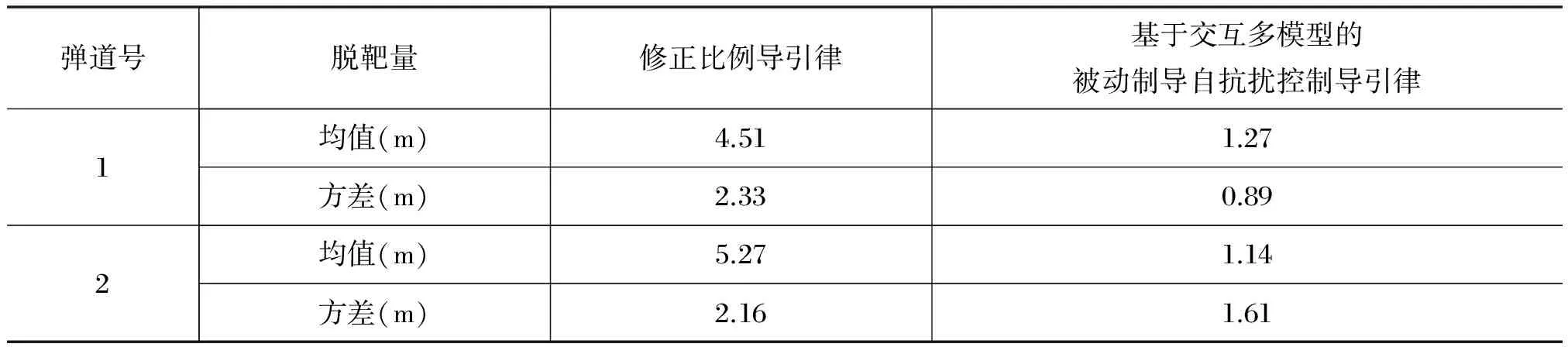
表2 100次蒙特卡洛仿真统计结果

由图5可知，在目标突然发生机动时，IMM_UKF算法能快速跟踪目标，算法及时收敛，与真实值误差小，滤波效果优于单模型UKF算法。由图7和图8可知，自抗扰导引律弹道末端过载发散小，导弹在运动过程中平稳高效，有很强的可靠性。表2结果显示，自抗扰导引律具有制导精度高、脱靶量小的优点，优于修正比例导引律。

5 结束语

本文采用IMM_UKF算法估计弹目相对速度、距离和目标加速度信息，并利用自抗扰控制算法设计能够实时估计并补偿系统不确定因素的导引律。仿真结果表明，基于IMM_UKF的自抗扰控制导引律能够有效可靠地对目标进行跟踪，不仅提高了滤波精度，而且提高了系统的鲁棒性，提升了导弹对付机动目标的能力。

[1] 周宏仁,敬忠良,王培德．机动目标跟踪[M]. 北京:国防工业出版社,1991.

[2] Li Cai-ju,Li Ya-an.Research of Comparative Analysis of Extended kalman Filter and Particle Filter[J].Technical Acoustics,2009,28(4):74-78.

[3] Sadeghi B,Moshiri B.Second order EKF and Unscented Kalman Filter fusion for tracking maneuvering targets[J].IEEE International Conference on Information Reuse and Integration, 2007,13(15):514-519.

[4] 王钊,李世华,费树岷.非奇异终端滑模导引律[J]. 东南大学学报,2009,39(9)：87-90．

[5] 王文文,刘晓利,李志坚.基于自抗扰控制的微型导弹导引控制一体化设计[J]. 指挥控制与仿真,2015,6(3):121-125.

[6] 王淑一,程杨,杨涤等. UKF方法及其在方位跟踪问题中的应用[J]．飞行力学，2003,21(2)：59～62.

[7] Moon J, Kim K, Kim Y. Design of missile guidance law via variable structure control[J]. Journal of Guidance, Control and Dynamics,2001,24(4)：659～664.

[8] 张平,董小萌,付奎生.机载/弹载视觉导引稳定平台的建模与控制[M]. 北京:国防工业出版社,2011.