滑移转向4WD车辆直接横摆力矩控制方法研究

洪 濡，胡广地

（西南交通大学 汽车研究院，成都 610031）

随着轮式机器人以及分布式驱动电动汽车相关技术的快速发展，一种全新的转向结构车辆，滑移转向分布式驱动车辆成为未来汽车发展的重要形式之一。该种汽车具有底盘机械结构简单，能量利用率高，纵向力分配灵活等优点，能够实现蟹型运动以及零半径转向等特殊运动方式，将在未来的军事作战、救援以及特殊复杂环境任务中发挥巨大的优势。卡内基梅隆大学成功研制了多用途滑移转向无人地面车“MULE”与“Crusher”[1-2]，国内对这方面的研究尚处于起步阶段。

对车辆动态参数的估计，如车辆轮胎力、轮胎滑移角以及轮胎侧偏刚度，对于提升车辆运动控制系统的稳定性和安全性尤为重要。车辆的这些动态参数一般很难由传感器直接测量，现有的相关研究是利用EKF算法[3]去估计这些不可测量的变量。BAFFET等[4-5]基于EKF算法建立了2WS传统转向结构下的车辆动态参数观测器，并对相应算法进行了相关试验验证。LUCET等[6-7]针对四轮及六轮滑移转向车辆，利用滑模变结构控制算法设计了车辆运动控制系统，以便对车速和转向进行实时控制。JACKSON等[8]采用模糊控制法建立了六轮驱动力和制动力分配准则，以便在保持车辆的期望横摆角速度下尽力改善整车的牵引性能。闫永宝等[9]和邹广才等[10]以轮胎利用率最小为优化目标，设计了车辆驱动力分配算法，最大程度上保证了轮胎与地面附着，提高了轮胎的利用率。

提出了一种基于EKF算法的轮胎侧偏刚度状态观测器，可在线辨识出车辆各轮轮胎力和轮胎侧偏角，计算出实时的各轮胎侧偏刚度，实现了车辆目标直接横摆力矩的在线更新，提高了目标直接横摆力矩的准确性与实时性，增强了车辆实现驾驶意图（目标车速与目标转弯半径）的能力。建立的全轮纵向力分配算法可根据不同的轮胎负载状况对不同轮胎进行相应的轮胎力分配，在有效降低轮胎负荷率的同时提高了车辆的运动稳定性。

1　车辆的动力学模型建立

建立了车辆四轮动力学模型，如图1所示。惯性坐标系被定义为，车身坐标系被定义为车身坐标系中的速度向量在惯性坐标系中的表达其转换矩阵为：

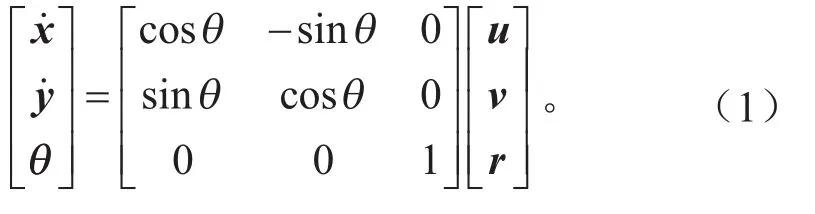
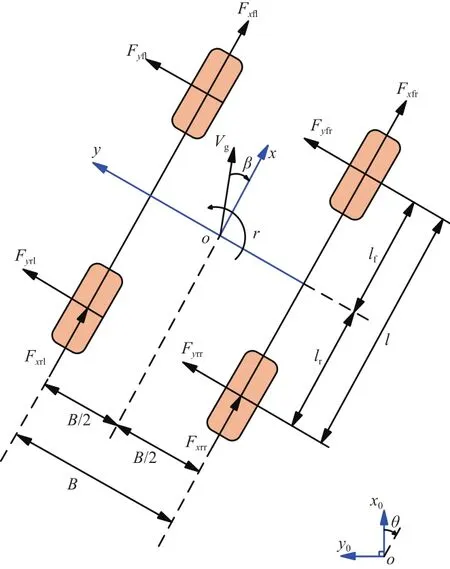
图1　车辆四轮动力学模型

在车身坐标系下，车辆模型的动力学方程如下：

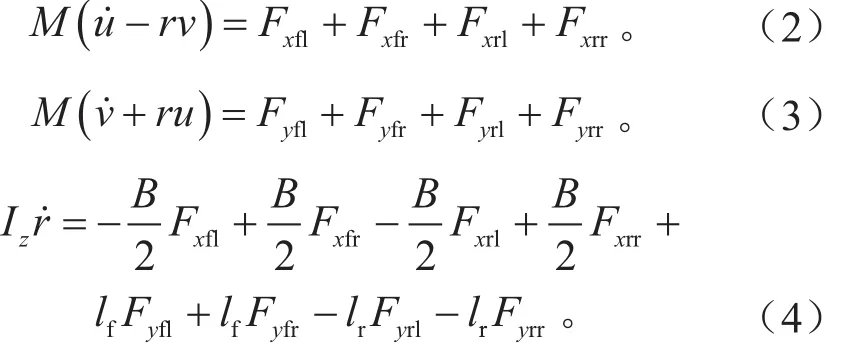
式（2）～（4）中：Fx**为轮胎纵向力；Fy**为轮胎侧向力；f、r 分别为前轮与后轮；l、r分别为左轮与右轮；M为整车质量；Iz为车辆绕z轴的转动惯量；lf为前轴到质心的距离；lr为后轴到质心的距离；B为左右轮的轮距。

2　运动控制系统的设计

由于滑移转向4WD车辆各轮纵向力独立且可控，所以运动控制系统设计的关键问题是如何根据车辆的运动控制目标（如车速、转向半径）计算出车轮纵向力所需要产生的横摆力矩，并利用一定的分配准则对各轮纵向力进行合理的分配。本研究设计的EKF状态观测器对车辆的轮胎侧向力、侧偏角以及侧偏刚度进行实时估计，提高了车辆侧向动力学模型的准确性与实时性。基于EKF状态观测器建立了车辆的运动系统控制系统，其结构简图如图2所示。

图2　运动控制系统的结构简图

2.1　基于EKF算法的车辆动态参数观测器的设计

在车辆的实际运动过程中，轮胎的侧偏刚度并非一个不变的常数，它受到如地面摩擦因数、轮胎垂直载荷等诸多因素的影响。本文中的轮胎侧偏刚度是计算目标横摆力矩的关键车辆参数，因此，对轮胎侧偏刚度这一动态参数进行实时在线估计，以提高目标横摆力矩计算值的实时性和准确性。采用线性轮胎模型，轮胎侧偏刚度可由下式计算：

式中：C**为轮胎的侧偏刚度；β**为轮胎的侧偏角。

在EKF观测器中，轮胎侧向力的动态演变模型采用的是随机游走模型。

根据上文建立的车辆动力学模型得出以下动态车辆参数关系。

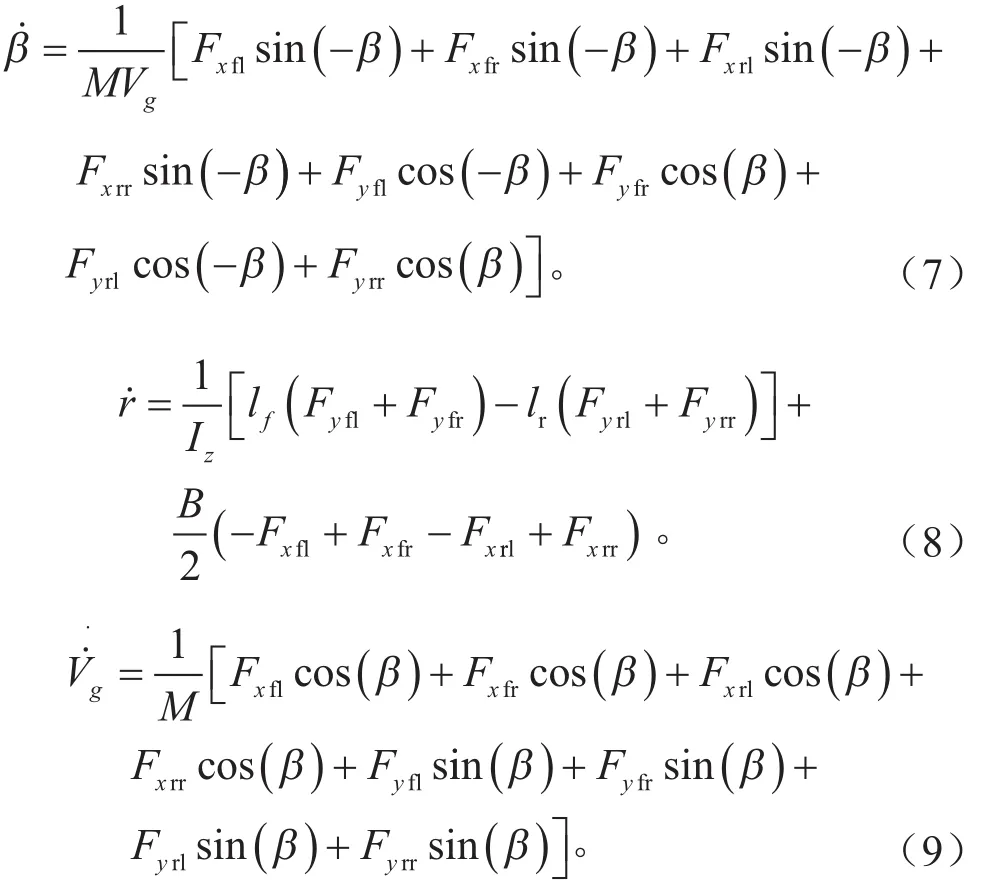
忽略了滚动和悬挂运动，车轮的垂直载荷具有以下负载转移形式。

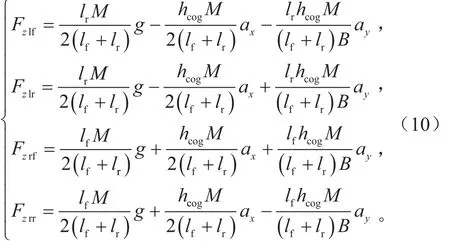
式中：g为重力加速度，约9.8 m/s2。

在EKF算法的状态量选取中，前轮轮胎侧向力的总和定义为Fyf，后轮轮胎侧向力的总和定义为Fyr，如式（11）所示。同时，各轮胎的侧向力可根据轮胎垂直力进行计算，如式（12）所示。

EKF观测器需要观测的状态变量包括质心侧偏角、横摆角速度、车身坐标系下车辆的绝对速度、前轮轮胎侧向力之和、后轮轮胎侧向力之和，定义状态变量X为：

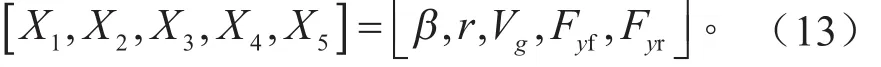
由于轮毂电机的驱动力矩和转速精度可确定，所以认为车轮纵向力是已知的，从而定义状态方程的输入变量U为：

根据式（6）～（9），状态方程表达式为：

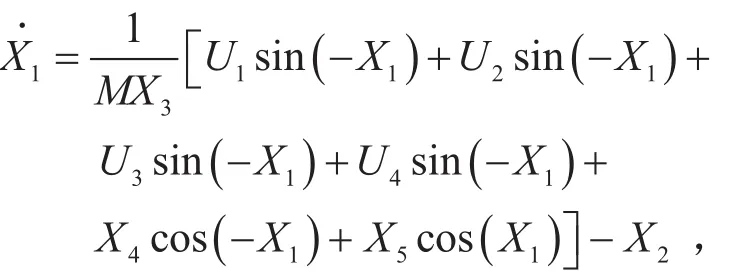
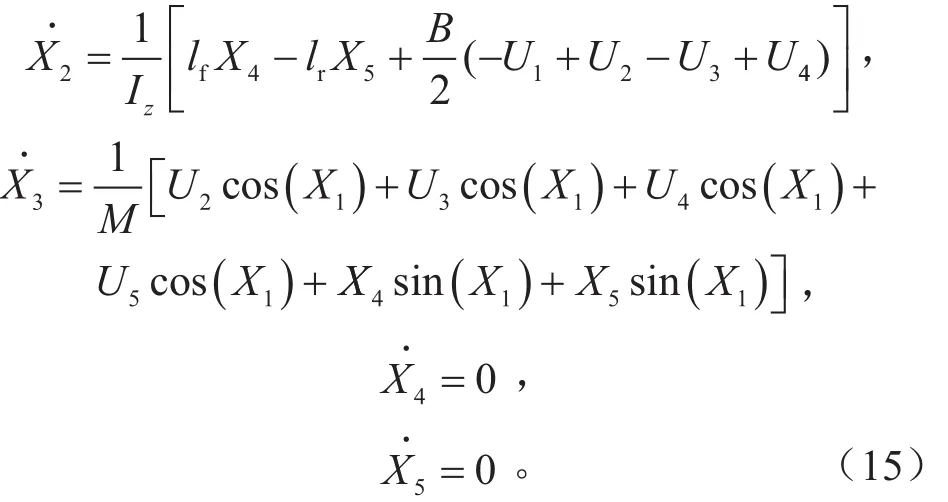
测量变量包括横摆角速度、车身坐标系下车辆的绝对速度、车身纵向加速度、车身侧向加速度，这些测量量可以通过安装在车上的惯性导航传感器（IMU）获得，定义测量变量Y为：

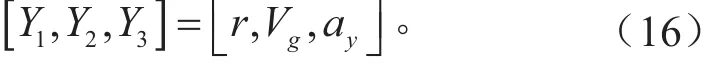
测量方程表达式为：

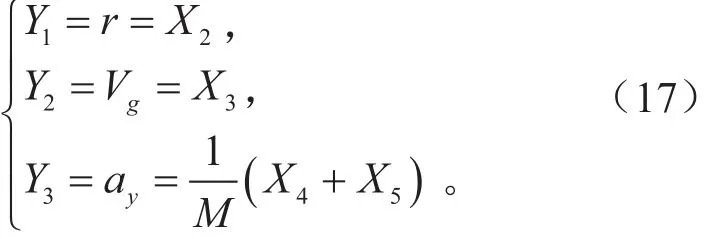
同时，轮胎的侧偏角可以由下式计算：

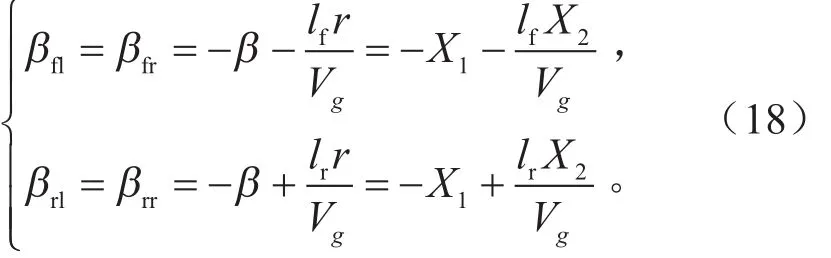
2.2　目标横摆力矩计算

定义方程（4）中由各轮轮胎纵向力Fx**所产生的横摆力矩之和为Mz，即：

利用上文中EKF观测器估计到的轮胎侧偏刚度C**作为已知常量式（5），并与式（3）、式（4）和式（19）联立得到含横摆力矩的车辆2-DOF动力学模型，如下：

由式（20）得到车辆稳态转向横摆角速度rss与Mz之间的关系为：

由稳态转向横摆角速度rss设计车辆目标稳态转向半径车辆目标横摆力矩Mzd与目标稳态转向半径Rd之间的关系如下：

2.3　各轮驱动力的控制分配

2.3.1目标纵向力需求设计

目标纵向力需求设计为开环，依靠驾驶员自身完成闭环控制。

式中：Fxd为整车目标纵向力需求；K为目标纵向力需求增益；αp为油门开度。

2.3.2各轮驱动力的控制分配约束条件

各轮驱动力在纵向的合力以及各轮驱动力所产生的横摆力矩之和与目标纵向力需求Fxd以及目标横摆力矩Mzd相等，其纵向力约束方程为：

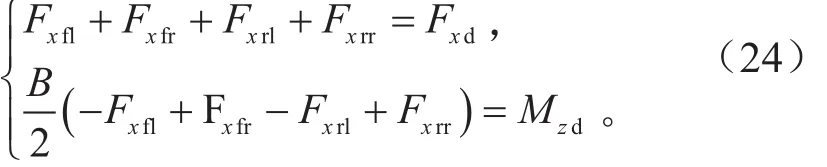
由式（24），令：

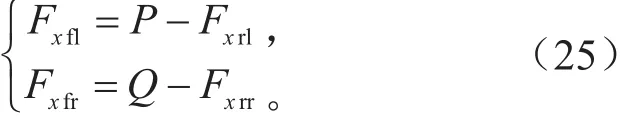
路面附着力和驱动电机的性能对纵向力的限制如下：式中：μ为路面的摩擦因数；Fm为电机能够转化为车轮上的最大驱动力。

2.3.3基于稳定性的纵向力优化分配算法

根据日本学者Masato Abe提出的以所有轮胎利用率平方和最小为目标函数来分配轮胎力的理念[11-12]，同时考虑各轮胎纵向力独立可控的特点，设计了纵向力优化分配的目标函数：

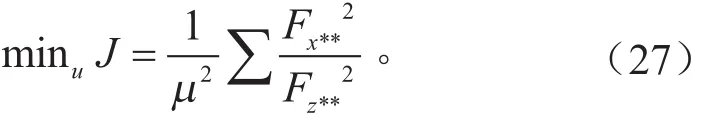
采用Lagrange乘子法求解，将式（25）代入式（27）中进行消元，计算出各轮胎纵向力分配结果：

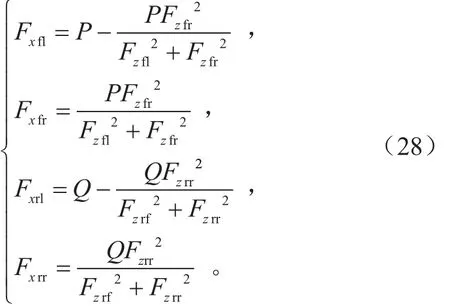
当路面附着条件较差时，即纵向力约束方程（24）出现空集，此时采用轴载比例分配算法，各轮胎力沿车身坐标系下纵向方向的合力为：

3　仿真与分析

利用专业车辆仿真软件Carsim与Matlab/Simulink进行联立仿真，在Carsim中设置车辆模型的相关参数与道路仿真环境，在Matlab/Simulink中设计运动控制系统的相关控制器，这种仿真方法能够充分地验证控制算法的准确性。车辆的主要仿真参数如下：整车质量质心到前轴的距离质心到后轴的距离整车绕质心的转动惯量前后轮距质心高度

仿真车辆在附着条件良好（摩擦因数为0.85）的路面上，分别以25 km/h和50 km/h的车速下匀速行驶，车辆所需的转向半径Rd如图3和图4所示。

图3　期望转向半径（25 km/h）

图4　期望转向半径（50 km/h）

3.1　基于EKF的轮胎侧偏刚度的估计仿真分析

利用Carsim软件中车辆的模型参数设置，输出各轮胎的侧偏角和侧向力作为车辆运行过程中的实际参考值。当期望车速为25 km/h时，算法的初始（30,0.02,0.02）。当期望车速为50km/h时，算法的初始值在期望车速为25 km/h的仿真工况下，各轮胎侧偏角与侧向力估计结果分别如图5和图6所示。在期望车速为25 km/h的仿真工况下，根据实时估计的各轮胎侧偏角和纵向力计算实时轮胎侧偏刚度，如图7所示。在期望车速为50 km/h的仿真工况下，各轮胎侧偏角与侧向力估计结果分别如图8和图9所示。在期望车速为50km/h的仿真工况下，根据实时估计的各轮胎侧偏角和纵向力计算的实时轮胎侧偏刚度如图10所示。

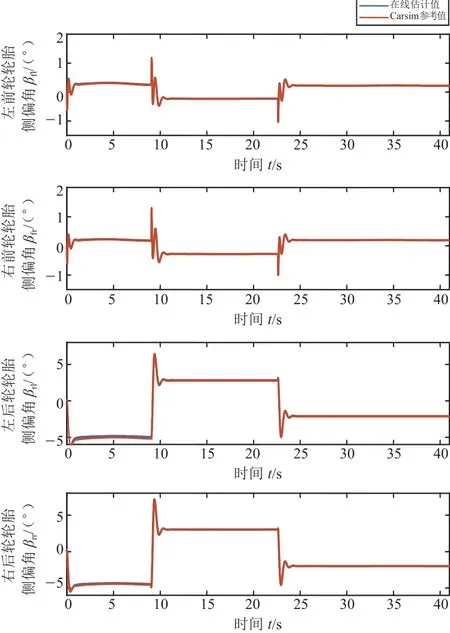
图5　轮胎侧偏角估计结果（25 km/h）

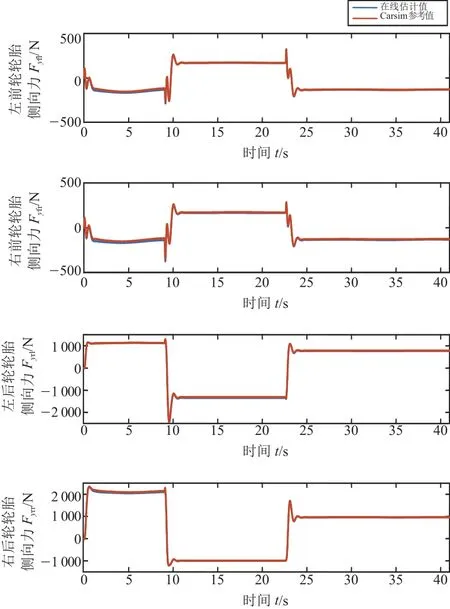
图6　轮胎侧向力估计结果（25 km/h）

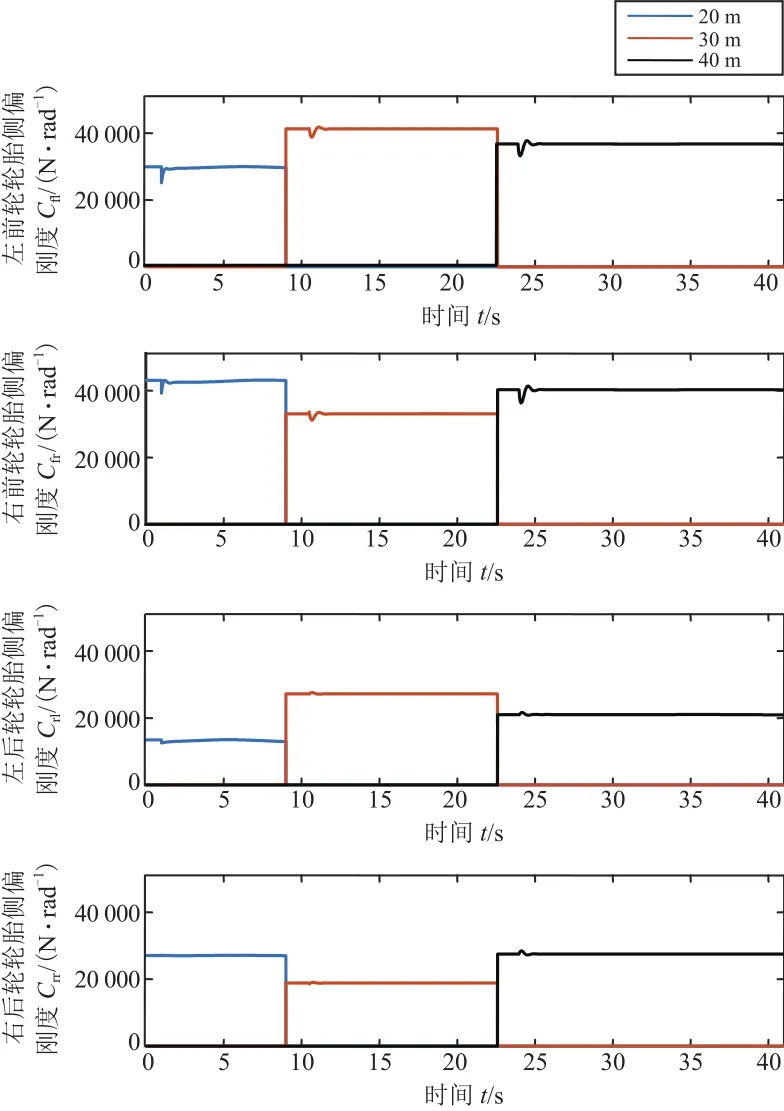
图7　轮胎侧偏刚度估计结果（25 km/h）

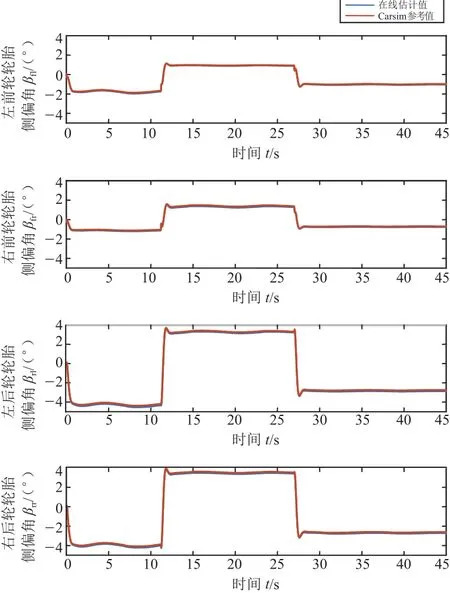
图8　轮胎侧偏角估计结果（50 km/h）

通过计算图5和图6，车辆在期望车速为25 km/h的工况下，由EKF滤波器估计的轮胎侧偏角和轮胎侧向力在各稳态转向过程中（期望转向半径分别为20 m、30 m、40 m）最大的实时误差率(估计值－参考值）/参考值，见表1和表2。通过计算图8和图9，车辆在期望车速为50 km/h的工况下，由EKF滤波器估计的轮胎侧偏角和轮胎侧向力在各稳态转向过程中最大的实时误差率εmax见表3和表4。

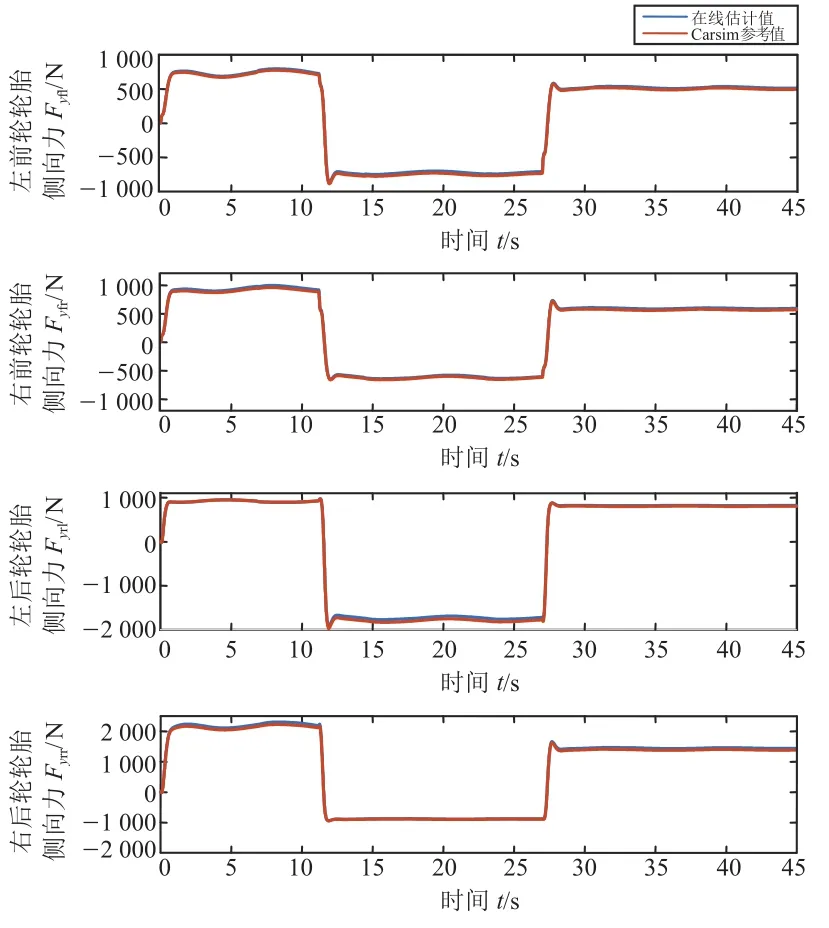
图9　轮胎侧向力估计结果（50 km/h）

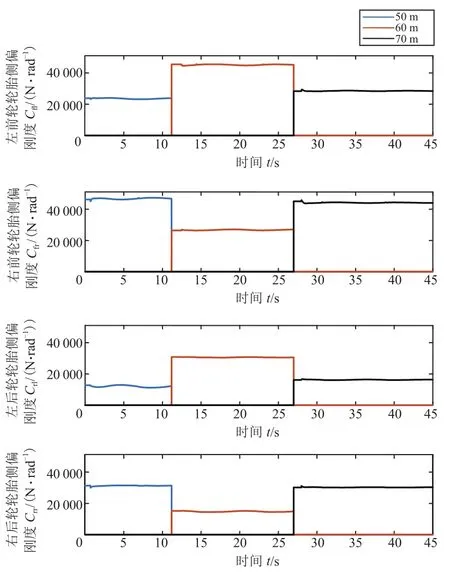
图10　轮胎侧偏刚度估计结果（50 km/h）

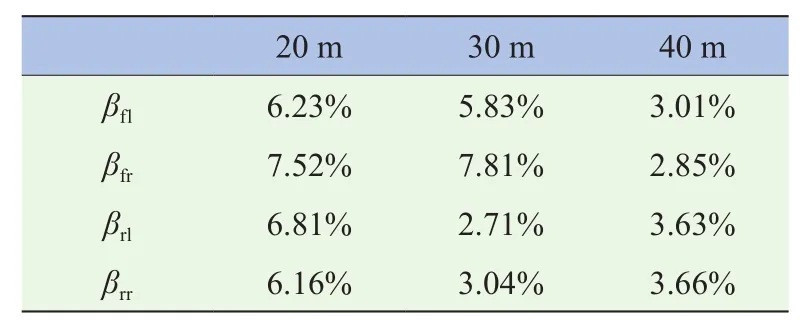
表1　轮胎侧偏角最大实时误差率εmax(25 km/h)

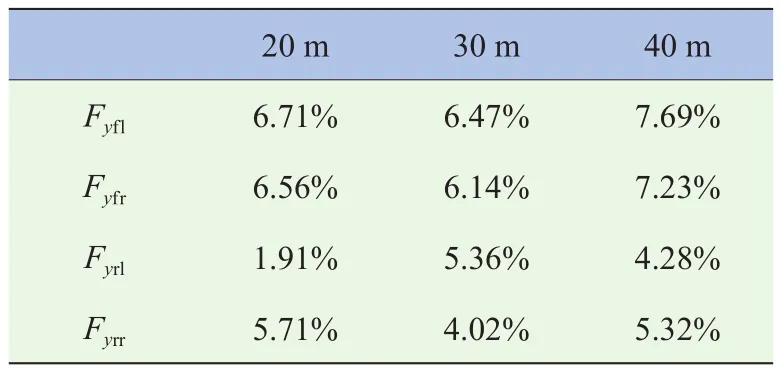
表2　轮胎侧向力最大实时误差率εmax(25 km/h)

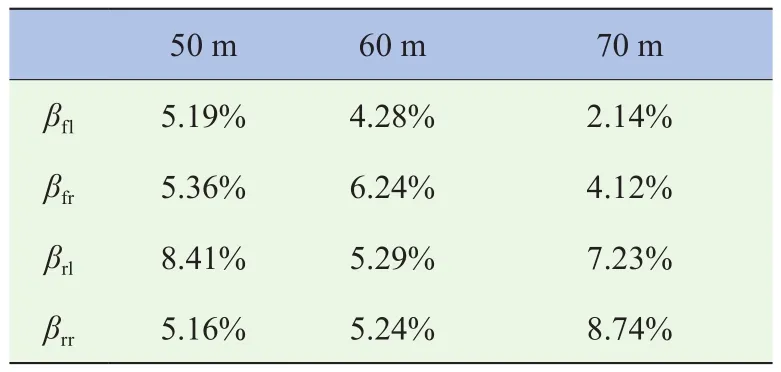
表3　轮胎侧偏角最大实时误差率εmax(50 km/h)

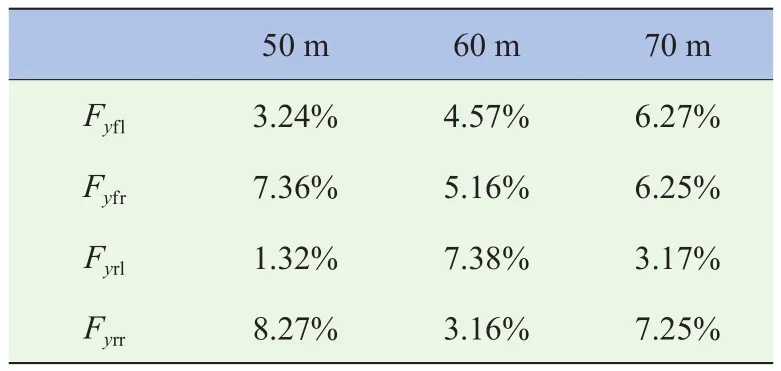
表4　轮胎侧向力最大实时误差率εmax(50 km/h)

由表1～4可知，车辆在低速（25 km/h）和中高速（50 km/h）两种稳态转向工况下，EKF滤波器的各轮胎侧向力、侧偏角估计值的最大实时误差率εmax都在8.5%以内。根据式（5）计算出的各工况下的轮胎侧偏刚度估计值，如图7和图10所示，具有很高的准确性与实时性，提高了车辆（含横摆力矩）2-DOF动力学模型和车辆横摆力矩计算值的准确性与实时性。

3.2　运动控制系统的仿真分析

图11和图12分别为车辆在期望车速为25 km/h和50 km/h工况下的相对应运动轨迹，以及基于期望车速和期望转向半径的参考路径与车辆实际运动路径之间的对比。图13、图14和图15、图16分别为车辆在期望车速为25 km/h和50 km/h工况下的实际运行过程中，实时车速、实时转向半径与期望车速、期望转向半径的实时误差。图17和图18分别为车辆在期望车速为25 km/h和50 km/h的工况下，基于控制分配算法的各轮胎纵向力的分配结果。

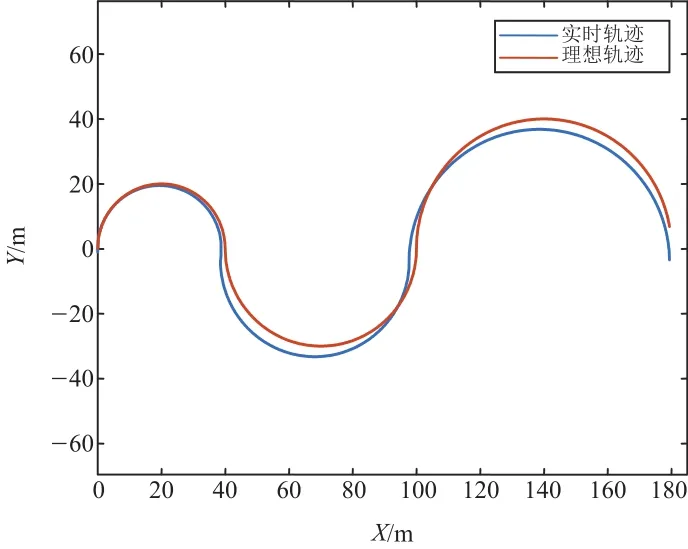
图11　车辆的运动轨迹（25 km/h）

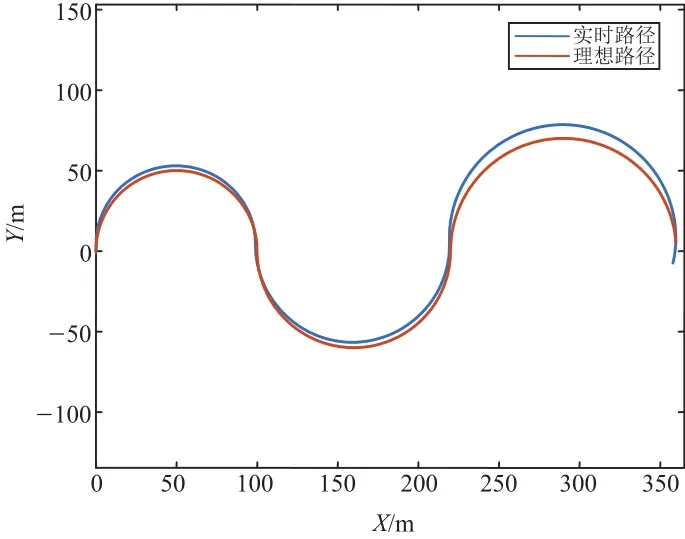
图12　车辆的运动轨迹（50 km/h）

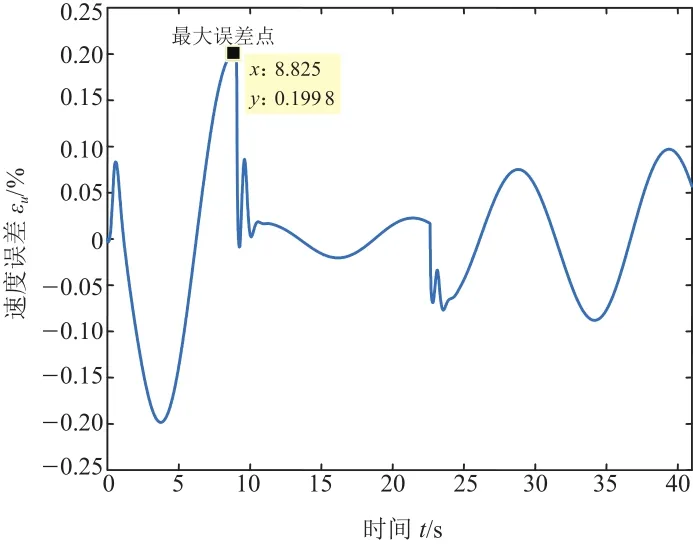
图13　速度实时误差（25 km/h）

图14　速度实时误差（50 km/h）

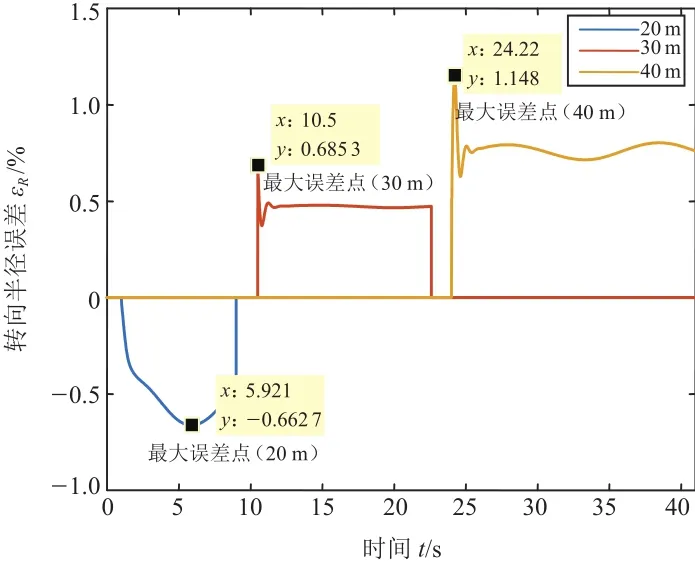
图15　转向半径实时误差（25 km/h）

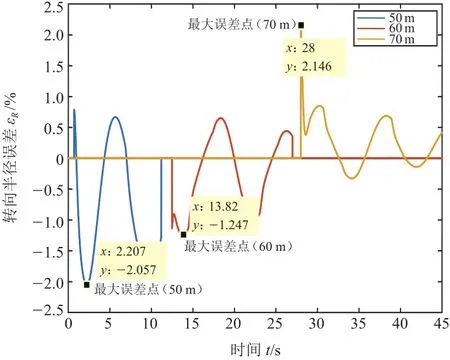
图16　转向半径实时误差（50 km/h）

图17　各轮胎纵向力的分配结果（25 km/h）

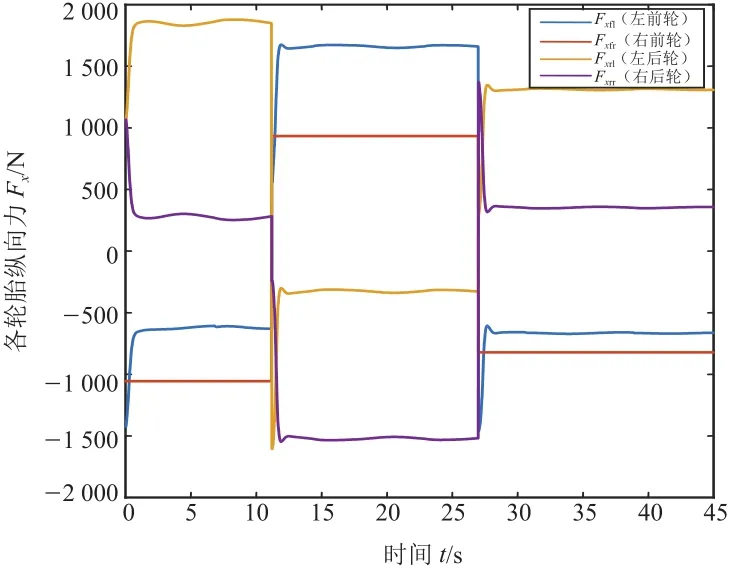
图18　各轮胎纵向力的分配结果（50 km/h）

由图11和图12可知，车辆实际的运行轨迹很接近车辆的理想运行轨迹，能够很好地实现车辆的驾驶意图。根据图13和图14中的最大误差点数据计算出车辆在期望车速为25 km/h和50 km/h的工况下，整个车辆运行过程中的实时车速与目标车速之间的最大实时误差率：εmax（25 km/h）为0.80%；εmax（50 km/h）为2.11%。根据图15和图16中的最大误差点数据计算出车辆在期望车速为25 km/h和50 km/h的工况下，转向半径的实时误差在各稳态转向过程中（25 km/h期望转向半径分别为20 m、30 m、40 m；50 km/h期望转向半径分别为50 m、60 m、70 m）的最大实时误差率：εmax（25 km/h）分别为3.31%，2.28%，2.87%；εmax（50 km/h）分别为4.11%，2.08%，3.07%。综上所述，从车速和车辆转向半径的最大实时误差率数据可以看出，车辆在低速（25 km/h）和中高速（50 km/h）两种稳态转向运动过程中，控制系统在实现车辆运动目标的同时还保证了车辆运动稳定性。车辆在低速（25 km/h）和中高速（50 km/h）两种稳态转向运动过程中，各轮驱动力的分配未出现高频抖振，表明了该驱动力分配算法在降低轮胎负荷率的同时还具有一定的实用性，如图17和图18所示。

4　结论

滑移转向分布式驱动车辆是未来特种车辆发展的重要形式，本文利用EKF算法建立了车辆关键状态参数观测器，设计了车辆的运动控制系统。通过Carsim与Matlab/Simulink的联立仿真结果分析与对比发现，设计的状态参数观测器能够准确、实时地对车辆关键动态参数进行在线估计，同时设计的车辆运动控制器在实现车辆运动目标的同时还保证了车辆的运动稳定性。在低速（25 km/h）和中高速（50 km/h）的仿真工况下，车辆期望速度以及期望转向半径最大实时误差控制在4.5%以内，很好地实现了驾驶目标。轮胎纵向力分配算法提高了轮胎的利用率。本文只考虑了车辆在稳态转向过程中的车辆运动控制系统的设计问题，对于车辆加速等瞬态情况并未考虑，同时，在对各车轮的纵向力分配算法设计中未能将车轮的最优滑移率考虑进去，未能实现车辆稳定性与动力性综合最优，因此，以后将对这些问题展开深入研究。

参考文献（References）：

[1]FAUROUX J C，VASLIN P. Modeling，Experimenting，and Improving Skid Steering on a 6 × 6 All-terrain Mobile Platform [J]. Journal of Field Robotics，2010，27(2)：107-126.

[2]MACLAURIN B. Comparing the Steering Performances of Skid-and Ackermann-steered Vehicles [J]. Proceedings of the Institution of Mechanical Engineers，Part D：Journal of Automobile Engineering，2008， 222(5)：739-756.

[3]GREWAL M S，ANDREWS A P. Kalman Filtering：Theory and Practice [M].[S.l.]：Prentice-Hall，1993.

[4]BAFFET G，CHARARA A，LECHNER D，et al. Experimental Evaluation of Observers for Tire-Road Forces，Sideslip Angle and Wheel Cornering Stiffness [J].Vehicle System Dynamics，2008，46(6)：501-520.

[5]BAFFET G，CHARARA A，LECHNER D. Estimation of Vehicle Sideslip，Tire Force and Wheel Cornering Stiffness[J]. Control Engineering Practice，2009，17(11)：1255-1264.

[6]LUCET E，GRAND C，SALLÉ D，et al. Dynamic Sliding Mode Control of a Four-wheel Skid-steering Vehicle in Presence of Sliding [C]// RoManSy'08：the 17th CISM-IFToMM Symposium on Robot Design，Dynamics，and Control，Tokyo，Japan：[s.n.]，2008.

[7]LUCET E，GRAND C，SALLÉ D，et al. Dynamic Yaw and Velocity Control of the 6WD Skid-steering Mobile Robot RobuROC6 Using Sliding Mode Technique [C]//Intelligent Robots and Systems， IROS 2009. IEEE/RSJ International Conference，10-15 Oct. 2009，St. Louis，MO. USA ：IEEE，2009：4220-4225.

[8]JACKSON A，CROLLA D，WOODHOUSE A，et al. Improving Performance of a 6×6 Off-road Vehicle Through Individual Wheel Control [C]// SAE Technical Papers，2002-01-0968，2002.

[9]闫永宝，张豫南，颜南明，等. 六轮独立驱动滑动转向车辆运动控制算法仿真研究 [J]. 兵工学报，2013，34(11)：1461-1468.YAN Yongbao，ZHANG Yunan，YAN Nanming，et al.Simulation Study of Motion Control Algorithm for a Sixwheel Independent Drive Skid-steering Vehicle [J]. Acta Armamentarii，2013，34(11)：1461-1468. (in Chinese)

[10]邹广才，罗禹贡，李克强. 基于全轮纵向力优化分配的4WD车辆直接横摆力矩控制 [J]. 农业机械学报，2009，40(5)：1-6.ZOU Guangcai，LUO Yugong，LI Keqiang. 4WD Vehicle DYC Based on Tire Longitudinal Forces Optimization Distribution [J]. Transactions of the Chinese Society of Agricultural Machinery，2009，40(5)：1-6.(in Chinese)

[11]MOKHIAMAR O，ABE M. How the Four Wheels Should Share Forces in an Optimum Cooperative Chassis Control [J].Control Engineering Practice，2006，14(3)：295-304.

[12]ABE M，KANO Y，SUZUKI K，et al. Side-slip Control to Stabilize Vehicle Lateral Motion by Direct Yaw Moment[J].JSAE Review，2001，22(4)：413-419.