DualSPHysics: A numerical tool to simulate real breakwaters *

Feng Zhang(张峰), Alejandro Crespo,Corrado Altomare ,José Domínguez,Andrea Marzeddu ,Shao-ping Shang(商少平) ,Moncho Gómez-Gesteira



DualSPHysics: A numerical tool to simulate real breakwaters*

Feng Zhang1(张峰), Alejandro Crespo2,Corrado Altomare3, 4,José Domínguez2,Andrea Marzeddu5,Shao-ping Shang1(商少平) ,Moncho Gómez-Gesteira2

1.2.3.4.5.

The open-source code DualSPHysics is used in this work to compute the wave run-up in an existing dike in the Chinese coast using realistic dimensions, bathymetry and wave conditions. The GPU computing power of the DualSPHysics allows simulating real-engineering problems that involve complex geometries with a high resolution in a reasonable computational time. The code is first validated by comparing the numerical free-surface elevation, the wave orbital velocities and the time series of the run-up with physical data in a wave flume. Those experiments include a smooth dike and an armored dike with two layers of cubic blocks. After validation, the code is applied to a real case to obtain the wave run-up under different incident wave conditions. In order to simulate the real open sea, the spurious reflections from the wavemaker are removed by using an active wave absorption technique.

SPH, DualSPHysics, wavemaker, wave run-up

Introduction

The DualSPHysics is an SPH-based model as an efficient and user-friendly numerical code for a wide range of applications in the field of hydraulic, naval and coastal engineering. Due to the power of the GPU (Graphics Processing Unit) cards with powerful pa- rallel computing capability, real engineering problems can be simulated with the DualSPHysics with a high resolution in a reasonable time. When applied to the coastal engineering, it is demonstrated that the model can accurately reproduce the wave propagation and transformation and the wave-structure interactions.

The DualSPHysics includes an implementation to generate regular and irregular waves with desired wave height and period. The code is designed to simu- late an experimental facility (the wave flume or the wave basin). Moving boundaries are used to simulate the displacement of the wavemaker in a physical facility. In the present study, a piston-type wavemaker that moves with a pre-imposed displacement is considered to generate regular wave trains. The DualSPHysics also includes systems of passive and active wave absorptions. The passive absorption is employed to avoid the wave reflection through a dissi- pative beach or sponge layers, while the active wave absorption is employed to absorb the reflected waves that travel back to the numerical piston. The details of the wave generation algorithms, the passive and active absorption techniques are described in Ref. [1].

The DualSPHysics code is used here to model the wave run-up over the breakwaters and the dikes. As a first step, the code is validated by experiments in a flume where the surface elevation, the wave orbital velocities and the wave run-up are obtained by simu- lating the interaction of the regular waves with a smooth and an armored breakwater. Once the code is validated with data from physical tests, the DualSPHysics is applied to simulate the interaction of realistic waves with an existing dike in the Chinese coast where the wave run-up is obtained under various incident wave conditions.

1. DualSPHysics model

The DualSPHysics[2,3]is developed by using the SPH technique for real engineering problems and to be run on either CPUs or GPUs. The GPUs offer now a higher computing power than the CPUs and they are an affordable option to accelerate the SPH computa- tion with a low economic cost. Thereby, the simula- tions can be performed using a GPU card installed on a personal computer[3].

The DualSPHysics is an open source software andcanbefreelydownloadedfrom www.dual.sphysics.org. The first validation of the GPU implementation of the code was presented in Ref. [4]. Recently, the DualSPHysics code was applied to coastal enginee- ring problems, e.g., to study the run-up on a real armour block coastal breakwater in Ref. [5] and to estimate the sea wave impact on coastal structures in Ref.[6] where the numerical results are validated with the experimental data for typical cases from the Belgian coast.

The main features of the DualSPHysics code are described in detail in Ref. [2] and we will only present the main features of the method.

1.1 SPH method

In the SPH, a fluid is described by replacing its continuum properties with locally smoothed quantities at discrete Lagrangian locations. Thus, the domain can be multiply-connected with no special treatment of the free surface, making it ideal for studying complicated flow situations.

The kernel functions play a fundamental role in the SPH method. They should be constructed by satis- fying several conditions such as the positivity, the compact support, the normalization, the monotonically decreasing and the delta function behaviour[7].

A Quintic kernel developed inRef. [8] is used in thesimulations

In the DualSPHysics, the Navier-Stokes equation is solved in a Lagrangian form:

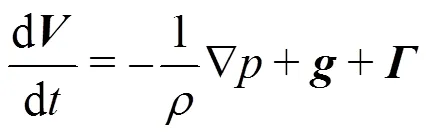
Therefore, the basic equations of conservation can be represented in the SPH notations[9]as

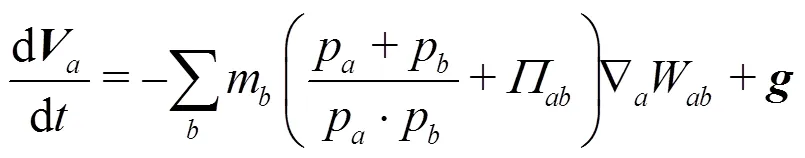
The changes of the fluid density are calculated by means of the differential equation given inRef. [9] instead of using a weighted summation of the mass terms, which would lead to an artificial density dec- rease near the fluid interfaces

The fluid is treated as weakly compressible in our approach, which allows the use of an equation of state to determine the fluid pressure, rather than solving an equation. However, the compressibility is adjusted to slow the speed of sound so that the time steps in the model (based on the sound speed) are reasonable.

The relationship between the pressure and the density is assumed to follow the equation of state as[11]

The Symplectic algorithm[12]is used in the present work to integrate variables in time. A variable time step is calculated according to Ref. [12], invol- ving the Courant-Friedrich-Lewy (CFL) condition, the force terms and the viscous diffusion term.

1.2 Boundary conditions

The dynamic boundary condition (DBC) is the default method provided by the DualSPHysics[13]. In this method, for the boundary particles, the same equations are satisfied as for the fluid particles, except that they do not move according to the forces exerted on them. Instead, they remain either fixed in position or move according to an imposed/assigned motion function (i.e.,as the moving objects such as the gates or the wave-makers). When a fluid particle appro- aches a boundary and the distance between the boun- dary particles and the fluid particles becomes smaller than twice the smoothing length, the density of the affected boundary particles increases, resulting in a pressure increase. In turn, we have a repulsive force exerted on the fluid particle due to the pressure term in the momentum equation. Validations with the dam-break flows and the sloshing tanks were made with good results as compared with other appro- aches[14].

1.3 Wave generation

The waves are generated in the DualSPHysics by means of moving boundaries to simulate the move- ment of a wavemaker as in physical facilities. The wave generation is made by using the moving boun- dary as piston-type and also flap-type wavemakers.

In this way, the wave height, the wave period and deptharethekeyinputparametersinthe DualSPHysics, and therefore, the time series of the wavemaker dis- placement is obtained by using the aforementioned wave theories.

1.4 Active wave absorption

2. Validation

The SPH results are compared with the experi- mental time series of the wave run-up for a smooth and armored dike. Numerical results of the wave run-up are validated against the data from physical model tests carried out at Maritime Engineering Laboratory (LIM) of the Universitat Politècnica de Catalunya (UPC). The small-scale wave flume named CIEMito is a part of the experimental infrastructures of LIM and is used for the purpose.

2.1 Initial setup

Fig. 1 Sketch of the wave flume with beach used in the SPH

Table1Wave conditions in the validation cases

2.2 Smooth dike: Exp. vs SPH

Fig. 2Comparison of the experimental and numerical surface elevations for WG6 with smooth dike

Fig. 3Comparison of the experimental and numerical run-ups for WG6 with smooth dike

The numerical model accuracy is estimated by calculating the relative error between the numerical wave run-up and the experimental one. For this purpose, two kind of calculations are performed. First, the maximum numerical wave run-up height in each test case is compared with the experimental one (Table 2). Then the average of all run-up events in each test case is calculated and the numerical average run-up height is compared with the experimental one (Table 3). The errors are, in general, smaller than 4%, except for WG1, where the numerical model underes- timates the wave run-up height. A bigger deviation in such a case is expectable due the fact that the plunging breaking involves very turbulent and random pro- cesses. However, repetition tests were not performed during the experiment, which makes it difficult to judge the accuracy of the physical modelling under such wave conditions.

Table 2Maximum wave run-ups for cases

2.3 Armored dike: Exp. vs SPH

The same initial configuration of the blocks in the experiment is considered in the simulations (Fig. 5). The positions of the cubic blocks of two layers are digitized and converted into a 3-D model (in the STL format),so that the pre-processing tools of the DualSPHysics can convert them into a set of boundary particles. The cubic blocks are considered fixed in the numerical modelling as in the physical model.

Fig. 4Initial setup of the experiment with the armored dike

Fig. 5(a)image of the blocks in the experiment

Fig. 5(b)STL model in DualSPHysic

The surface elevation at different positions along the wave flume, the wave orbital velocities and the wave run-up at the location of the dike are numeri- cally computed and compared with the experimental data performed in the CIEMito flume. Figure 6 plots the time series of the surface elevation at WG1, WG2, WG3 and WG4 and a very good agreement is obser- ved between the SPH calculations and the experi- mental results.

The horizontal orbital velocity computed at V1 andV2intheDualSPHysicsisshowninFig.7andcompared with the experimental model results. The experimental results show some spikes, especially at the beginning of the time series. Notwithstanding, the average harmonic behavior is still visible and matches the numerical results. Vertical velocities cannot be compared because of inaccuracies of the measurement system.

Fig. 6Comparison of the experimental and numerical surface elevation for WG1 with armored dike

Fig. 8 (Color online) Wave gauges in the armored dike during the experiment

The run-up is computed in the DualSPHysics model at 52 positions along the width of the tank to catch the 3-D behavior. However only two positions are used in the experiments. These two filaments are marked in Fig. 8. Hence, the black line in Fig. 9cor- responds to the average of the measurements by the two experimental probes while the different red lines correspond to the different numerical measurements. The analysis of Fig. 9 indicates that DualSPHysics is capable to represent the time history of the wave run-up on an armored dike.

Fig. 9Comparison of the experimental and numerical run-ups for WG1 with armored dike

3. Model application

The DualSPHysics model is properly validated with experiments of wave run-ups as shown before. In this section, the model is applied to study the real si- tuations in the Chinese coast, in particular, in the coast of Chongwu with a dike. The SPH modelling will allow us to computethe wave run-ups in this dike under realistic wave conditions. A picture of the dike is shown in Fig. 10, which is located in Fujian pro- vince, made of cement with steps.

Fig. 10(Color online) Picture of the dike in the coast of Chongwu

Fig. 11 (Color online) Initial setup of the case of application

Table 4Maximum wave run-ups for cases

Fig. 12 Numerical domain to study wave propagation

Figures 13 and 14 show the numerical and theo- retical time series of the surface elevation at locations 45 m, 68 m and 90 maway from the piston for Regular Wg1 andat locations 33 m, 66 m and 99 m for WG2, respectively. Figures 15 and 16 show the numerical and theoretical results for irregular waves. The SPH results follow the Stokes 2ndorder wave theory in terms of the surface elevation, so it is demonstrated that the waves are properly generated and propagated.

A sponge layer is used in the numerical tank to avoid the wave reflection. Table 5 shows the reflec- tion coefficients (CR) in both regular and irregular wave cases. The wave reflection is considered very weak with the values of CR lower than 10%.

Fig.13Comparison of the experimental and numerical surface elevations for regular WG1 with sponge layer

Fig.14Comparison of the experimental and numerical surface elevations for regular WG2 with sponge layer

Table 5Values of reflection coefficients with passive wave absorption

Once the wave generation and propagation are proven to be accurate, theinteractionbetweenrealistic waves and a dike in the coast of Chongwu can be studied with the DualSPHysics. The AWAS is now employed to absorb the reflected waves at the piston in order to simulate the behavior of an open sea where the reflected waves propagate outside the simulated domain. The setup shown in Fig. 17 represents the case of study.

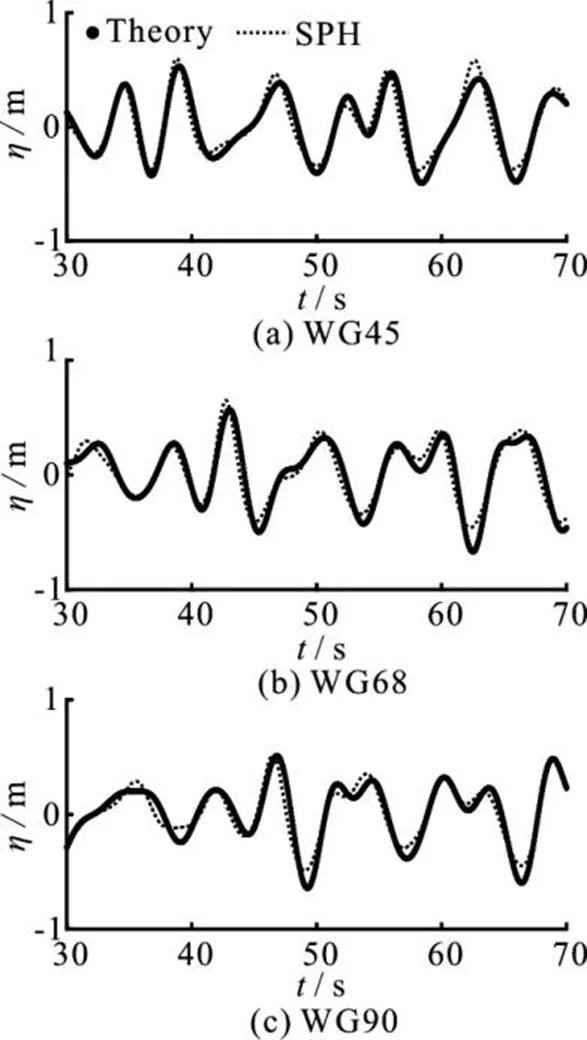
Fig.15Comparison of the experimental and numerical surface elevations for irregular WG1 with sponge layer

Fig.16Comparison of the experimental and numerical surface elevations for irregular WG2 with sponge layer

It is necessary first to prove that the use of the AWASsystemcanavoidthere-reflectionandonly the desired incident waves are interacting with the real dike. Figures 18 and 19demonstratethatthesurface elevation of regular waves by using the AWAS has oscillations of the same amplitude and period, as it should be expected if the re-reflection at the piston is observed. Note that when the AWAS is not employed, the surface elevation at different locations becomes chaotic without a regular pattern.

Fig.17Numerical domain to study wave-dike interaction

Fig.18Comparisonofthenumericalsurface elevations obtained with and without AWAS for regular WG1

Fig.19Comparison of the numerical surface elevations obtained with and without AWAS for regular WG2

Fig. 21 Comparison of the numerical forceson the structure obtained with and without AWAS for regular WG1

Fig. 22 Comparison of the numerical forceson the structure obtained with and without AWAS for regular WG2

Fig. 23 Spectrum analysis of incident wave for irregular WG1

The third way to prove the correct behavior of the AWAS is to compute the forces on the dike. If the re-reflection is removed, the regular cycles are obser- ved in the time series of the force, as it can be obser- ved in Figures 21 and 22 for regular WG1 and WG2, respectively.

Fig. 24 Spectrum analysis of incident wave for irregular WG2

Fig. 25 Time series of the wave run-up with regular WG1 and WG2

After all these analyses, we can assume that the numerical tank can simulate a real sea state since the piston with the AWAS reproduces the behavior of an open sea. Therefore, we can now compute the values of the wave run-up at the dike. Figures 25 and 26 show the time series of the numerical run-up com- puted with the DualSPHysics for regular waves and irregular waves, and under the two incident wave conditions.

Fig. 26 Time series of the wave run-up with irregular WG1 and WG2

The values of the maximum wave run-up height in case of regular and irregular wave trains are shown in Table 6.

Table 6Maximum wave run-up in the case of study

4. Conclusions

In the first part of this paper, the DualSPHysics code is validated in terms of the wave run-up on a breakwater. The numerical results are compared with experimental data of a smooth dike and a dike with two layers of cubic blocks. Several different wave conditions are simulated and an overall good accuracy is obtained for the wave surface elevation, the velo- cities and the time series of the run-up.

The comparison of the numerical and experi- mental time series of the wave run-up, not only averaged but also their significant values, features the present work. Previous work with the DualSPHysics[5], in fact, is a validation for the run-up where only a maximum values for different incoming waves are compared with experimental and literature data.

In the second part of this paper, the SPH code is applied to study a case of coastal engineering, using the real dimensions of a dike, the bathymetry and the wave conditions from the coast of Chongwu in China. In this case the wave conditions are imposed based on the real wave conditionsand the AWAS is employed to compensate the wave reflection at the numerical wavemaker (This is mandatory to simulate the real open sea).

The DualSPHysics is properly validated with experiments and it can be applied to study real situa- tions in the coast of China.

Acknowledgement

This work was supported by the Xunta de Galicia (Spain) under project ED431C 2017/64 “Programa de Consolidación e Estructuración de Unidades de Investigación Competitivas (Grupos de Referencia Competitiva)” co-funded by European Regional Development Fund (FEDER) and under project “NUMANTIA ED431F 2016/004”. The work is also funded by the Ministry of Economy and Competi- tiveness of the Government of Spain under project “WELCOME ENE2016-75074-C2-1-R”.

[1] AltomareC., DomínguezJ.M., CrespoA.J.C. et al.Long-crested wave generation and absorption for SPH-based DualSPHysics model [J]., 2017, 127(7): 37-54.

[2] CrespoA.J.C., DomínguezJ.M., RogersB.D. et al. DualSPHysics: open-source parallel CFD solver on SPH [J]., 2015, 187(2): 204-216.

[3] DomínguezJ.M., CrespoA.J.C., Valdez-BalderasD. et al.New multi-GPU implementation for smoothed par- ticle hydrodynamics on heterogeneous clusters [J]., 2013, 184(8): 1848-1860.

[4] CrespoA.J.C., DomínguezJ.M., BarreiroA. et al. GPUs, a new tool of acceleration in CFD: Efficiency and reliability on smoothed particle hydrodynamics methods [J]., 2011, 6(6): e20685.

[5] AltomareC., CrespoA.J.C., RogersB.D. et al. Nume- rical modelling of armour block sea breakwater with smoothed particle hydrodynamics [J]., 2014, 130(1): 34-45.

[6] AltomareC., CrespoA.J.C., DomínguezJ.M. et al. Applicability of smoothed particle hydrodynamics for estimation of sea wave impact on coastal structures [J]., 2015, 96(2): 1-12.

[7] LiuG.R., LiuM.B. Smoothed Particle Hydrodynamics: a meshfree particle method [M].Singapore: World Scienti- fic, 2003.

[8] WendlandH. Piecewiese polynomial, positive definite and compactly supported radial functions of minimal degree [J]., 1995, 4(1): 389-396.

[9] MonaghanJ.J. Smoothed particle hydrodynamics [J]., 1992, 30(1): 543-574.

[10]MonaghanJ.J. Smoothed particle hydrodynamics [J]., 1992, 30: 543-574.

[11] BatchelorG.K. Introduction to fluid dynamics [M]. Cam- bridge, UK: Cambridge University Press, 1974.

[12]LeimkuhlerB.J., ReichS., SkeelR.D. Integration methods for molecular dynamic IMA volume in mathe- matics and its application [M]. New York, USA: Springer, 1996.

[13] CrespoA.J.C., Gómez-GesteiraM., DalrympleR. Boun- dary conditions generated by dynamic particles in SPH methods [J]., 2007, 5(3): 173-184.

[14] DomínguezJ.M., CrespoA.J.C., Cercós-PitaJ.L. et al. Evaluation of reliability and efficiency of different boun- dary conditions in an SPH code [C]., Parma, Italy, 2015.

[15] MadsenP. A., FuhrmanD. R., SchäfferH. A. On the soli- tary wave paradigm for tsunamis [J]., 2008, 113(C12): 1-22.

[16]LiuZ., FrigaardP. Generation and analysis of random waves, generation and analysis of random waves [R]. Aalborg, Denmark: Aalborg Universitet, 1999, 79.

[17]Barthel F. C., Mansard V., Sand E. P. et al. Group bounded long waves in physical models [J]., 1983, 10(4): 261-294.

[18] SchafferH.A., KlopmanG. Review of multidirectional active wave absorption methods [J]., 2000, 126(2): 88-97.

[19] DidierE., NevesM.G. A Semi-Infinite numerical wave flume using smoothed particle hydrodynamics [J]., 2001, 22(3): 193-199.

[20] MadsenO.S. On the generation of long waves [J]., 1971, 76(36): 8672-8683.

(October 22, 2017, Accepted December 14, 2017)

©China Ship Scientific Research Center 2018

* Project supported by the National Key R&D Program of China (Grant No. 2017YFC1404801).

Feng Zhang (1989-), Male, Ph. D. Candidate,

E-mail: zhangfeng@stu.xmu.edu.cn

Shao-ping Shang,

E-mail:spshang@xmu.edu.cn