Numerical study of the wave-induced slamming force on the elastic plate based on MPS-FEM coupled method *

Cheng-ping Rao (饶成平), De-cheng Wan (万德成)



Numerical study of the wave-induced slamming force on the elastic plate based on MPS-FEM coupled method*

Cheng-ping Rao (饶成平), De-cheng Wan (万德成)

Slamming is the phenomenon of structure impacting the water surface. It always results in the extremely high load on the structure. This paper is mainly concerned with the slamming force caused by the wave-plate interaction. In this paper, the process of solitary wave impacting onto the horizontal plate is simulated with the help of the moving particle semi-implicit and finite element coupled method (MPS-FEM). The MPS method is adopted to calculate the fluid domain while the structural domain is solved by FEM method. In the first series of simulations, the profiles of the solitary waves with various amplitudes, which are generated in the numerical wave tank, are compared with the theoretical results. Thereafter the interaction between the solitary waves and a rigid plate is simulated. The effects of wave amplitude, as well as the elevation of the plate above the initial water level, on the slamming force are numerically investigated. The calculated results are compared with the available experimental data. Finally, the interactions between the solitary waves and the elastic plate are also simulated. The effects of the structural flexibility on the wave-induced force are analyzed by the comparison between the cases with elastic and the rigid plate.

Slamming, moving particle semi-implicit (MPS), finite element method (FEM), fluid-structure interaction, MPSFEM- SJTU solver

Introduction

The wave-structure interaction is a particularly topical issue in the field of naval architecture and ocean engineering. The plate structure, such as the pier, trestle bridge or very large floating structure (VLFS), is among the most common structures suffering from the impact of the waves. The severe wave may cause considerable deformation or failure of the offshore and costal structures. The research on the slamming force during the wave-plate interaction is crucial to the design of the offshore or costal structures.

Since the numerical simulations can provide researchers with comprehensive information and con- sume much less resources than experiments, a variety of numerical methods are developed to investigate the wave-plate interaction, especially the slamming force in this process. To name some of them, Seiffert et al.[1]analysed the slamming force on a flat plate under the solitary wave based on the finite-volume method (FVM) with the help of the open source computational fluid dynamics (CFD) platform-OpenFOAM. Greco et al.[2]employed the boundary element method (BEM) to investigate the coupling between the motion of a VLFS and the bottom slamming force. However, the aforementioned researches ignored the flexibility of the plate. Actually, the deformation of the structure could exert significant influences on the flow and the slamming force. According to Abrate’s statement[3], the vibration of the elastic structure could cause the oscillation of the slamming force. To take the structu- ral deformation into consideration, scholars are requi- red to implement structure calculation on the basis of original CFD solvers. Liu and Sakai[4]studied the hydroelastic responses of a 2-D flexible plate exposed to waves based on the BEM and the FEM. Korobkin and Khabakhpasheva[5]studied the regular waves im- pacting on an elastic plate in the context of linear potential-flow theory and Euler beam theory. Liao and Hu[6]combined the finite difference method (FDM) with the FEM method to investigate the interplay between the surface flow and a thin elastic plate.

In general, the problems in the naval architecture and ocean engineering can be characterized by free surface, multiphase flow or material discontinuities[7]which require extra treatments on tracking the boun- daries of water surface and structure. Despite the mesh-based methods are of effectiveness in the simu- lation of fluid evolution, they may suffer from the difficulties such as the adjustment or regeneration of mesh while tracking the complex boundaries. Owing to the Lagrangian property, some newly emerged mesh-free methods can exactly overcome the difficul- ties regarding the mesh-based method. The smoothed particle hydrodynamics (SPH)[8,9]and the moving par- ticle semi-implicit (MPS) method[10]are two typical particle-based mesh-free methods. These mesh-free methods demonstrate many advantages while dealing with the problems of large deformation or intense free surface because the boundaries of material can be tracked by particles automatically[11]. Although the SPH-FEM model was first proposed by Attaway et al.[12]to investigate the structure-structure interaction, it was subsequently applied into fluid-structure inte- raction (FSI) problems by scholars[13-15].

Some preliminary researches on FSI have been conducted in the context of the MPS method. Sun et al.[16]proposed MPS-modal superposition method in which the elastic deformation of structure is computed through a mode superposition formulation. In contrast, more scholars chose to combine the MPS with the FEM method in order to address complicated FSI problem. Lee et al.[17]successfully simulated the inte- raction between dam-break and sloshing flow through the coupled MPS-FEM method. Rao et al.[18]investi- gated the solitary wave impact onto a vertical elastic plate using our in-house MPSFEM-SJTU solver[18-21]. Some other researches performing the MPS-FEM model[19, 22, 23]also displayed fair agreement with avai- lable experimental results.

The present paper aims at investigating the slam- ming force during the interaction between the solitary wave and a horizontal elastic plate numerically. The theories of our in-house solver MPSFEM-SJTU, as well as its coupling strategy, are introduced. Then the performance of the solitary wave generation is ex- amined to make sure that desired wave can be gene- rated. In the FSI analysis, the interaction between the solitary wave and rigid plate is simulated. The wave amplitude, together with the vertical position of the plate, varies in different cases in order to investigate their effects on the wave-induced slamming force. Finally the solitary wave impacting onto the elastic plate is investigated. The peculiar phenomena in the elastic case are primarily discussed.

1. Numerical methods

1.1 The moving particle semi-implicit method

1.1.1 Governing equations

The governing equations of viscous incompres- sible fluid are composed of continuity equation and Navier-Stokes equation:

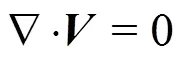
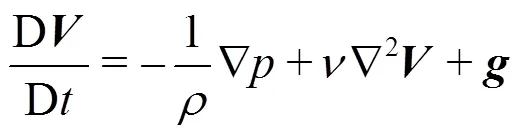
1.1.2 Models of particle interaction

In particle-based method, the fluid domain is rep- resented by thousands of particles. Thus, the governing equations are required to be transformed into the form of particle interactions. The particle interaction models are implemented based on the kernel function. In present paper, a modified kernel function proposed by Zhang and Wan[24]is adopted.

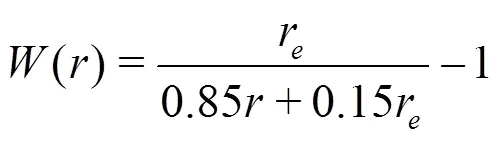
1.1.3 Models of mathematical operator

In MPS method, the models of particle interaction involve gradient model, divergence model and Laplacian model. They are written as:

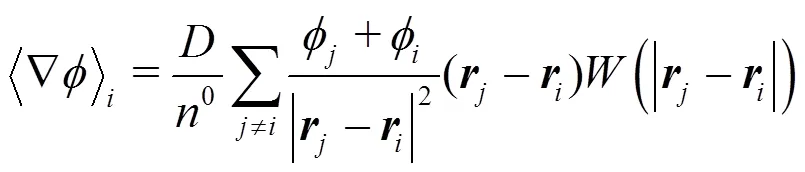
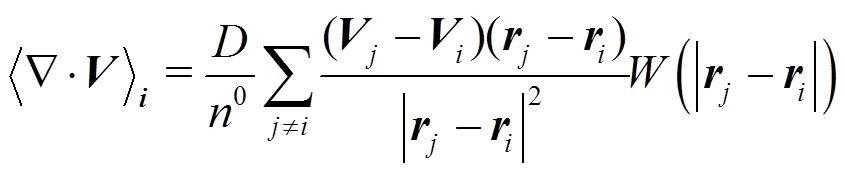
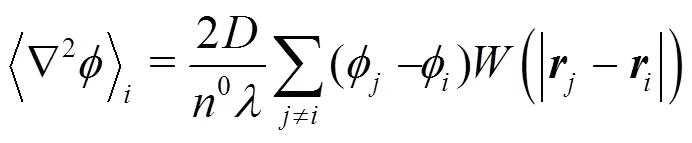
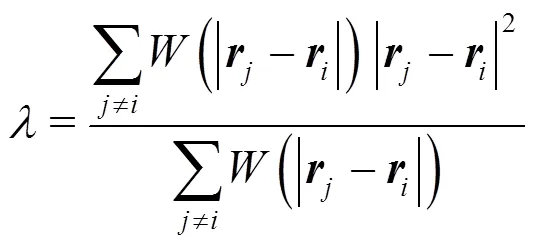
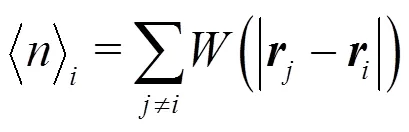
1.1.4 Model of incompressibility

As mentioned before, the MPS method is used to simulate the incompressible flow. To impose the in- compressibe condition on the fluid, the semi-implicit algorithm is adopted and the pressure of each particle can be obtained through solving the Poisson’s pressure equation (PPE). In this paper, we employ a mixed source term method combining the velocity diver- gence-free condition and the constant particle number density condition. It is proposed by Tanaka and Masunaga, and rewritten by Lee et al.[25, 26]

Table1Computational parameters for MPS

1.1.5 Detection of surface particles

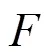
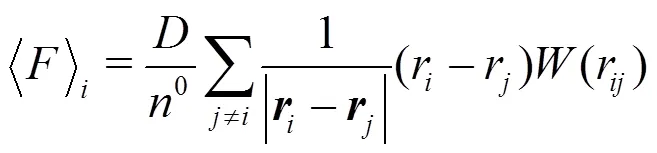
1.1.6 Solving procedure of MPS

In the solving procedure of MPS method, the pro- jection-correction algorithm is employed. The proce- dure is presented step by step as follows:

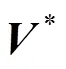
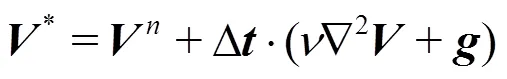
(3) Solve the Poisson’s pressure equation and obtain the particle pressure at next time step.

(4) Correct the velocity and position of particles implicitly based on the obtained pressure

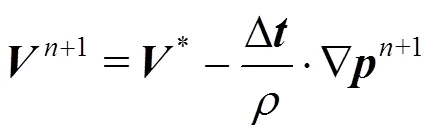
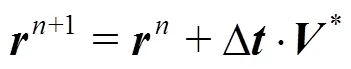
1.2 The finite element method

According to the FEM theory, the spatially discre- tized structural dynamic equations, which governing the motion of structural nodes, can be expressed as[27]:

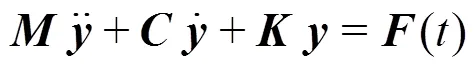
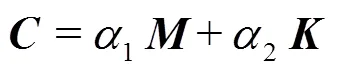
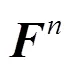
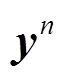
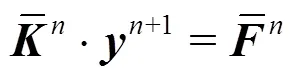
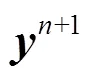
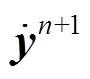
Detailed calculating equations can be found in our previous publication[29].

1.3 Partitioned coupling strategy for FSI

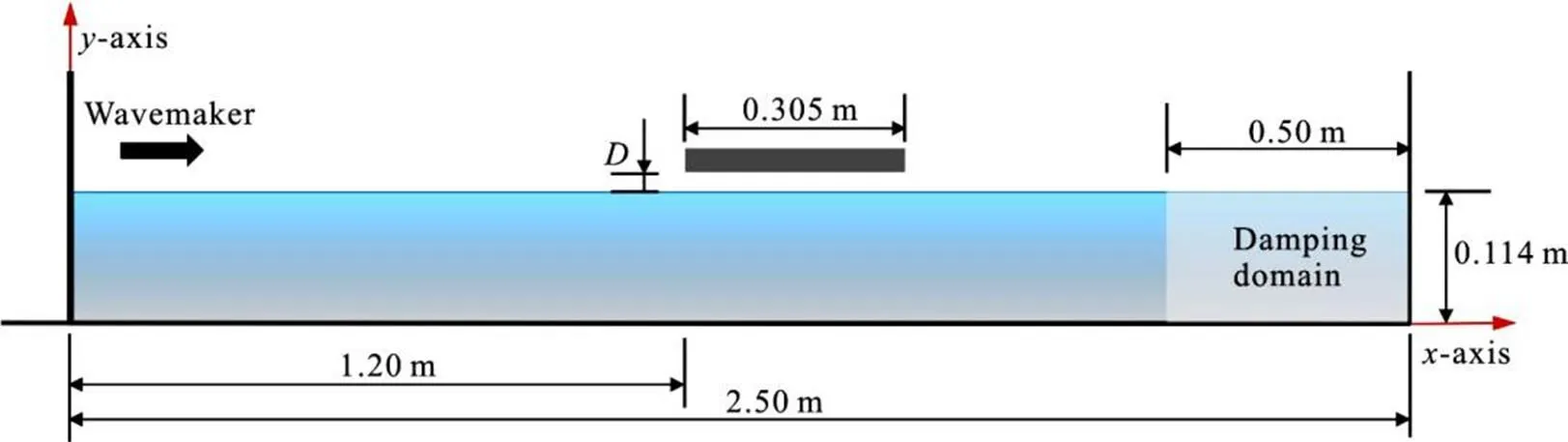
Fig. 2(Color online) Geometric model of the numerical wave tank

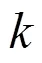
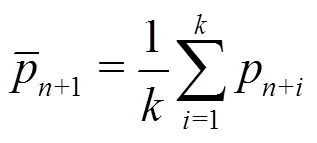
On the other hand, to impose the boundary con- dition of structure domain on the fluid, the structure domain is updated every structural timestep. It should be noted that the boundary particles are involved in the solving of Poisson’s pressure equation. In this way, the boundary information of structure domain can be passed to the fluid domain successfully.

2. Numerical simulations

The interaction between the solitary wave and a horizontal plate is simulated using the in-house solver in this section. The geometric model of the wave tank, aswellasthehorizontalplate,isdepictedinFig. 2.

Fig. 3Comparison of the wave profile between the calculated and theoretical solution

2.1 Numerical wave generations

Figure 3 shows the comparison of the wave pro- file between the numerical simulation and the theore- tical solution. It can be seen that the wave crest of the simulation agrees well with the theoretical solution presented by Goring[30]. Besides, there is no evident decay in the wave crest as it propagates downstream. However, there are still some slight distinctions, such as in the ascending portion of the curve, owing to the finite length and depth of the wave tank. It can be concluded that desired solitary wave can be generated based on MPS method.

2.2 Interaction between waves and a rigid plate

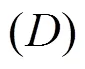
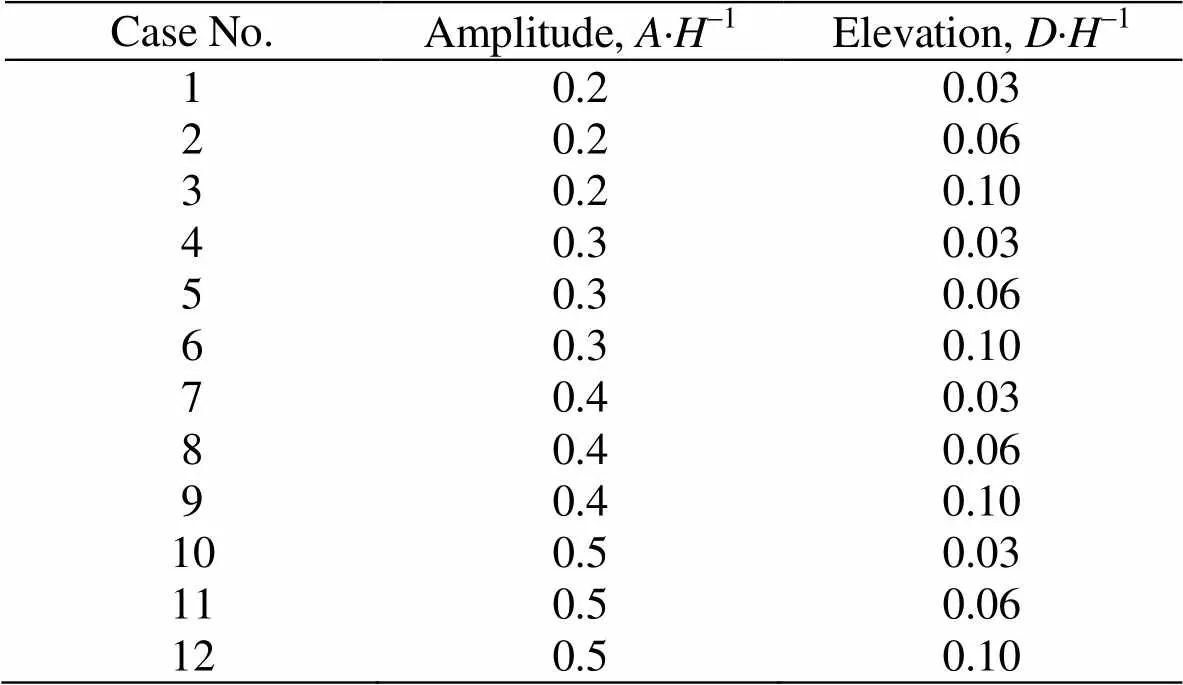
Table2Configurations in all cases

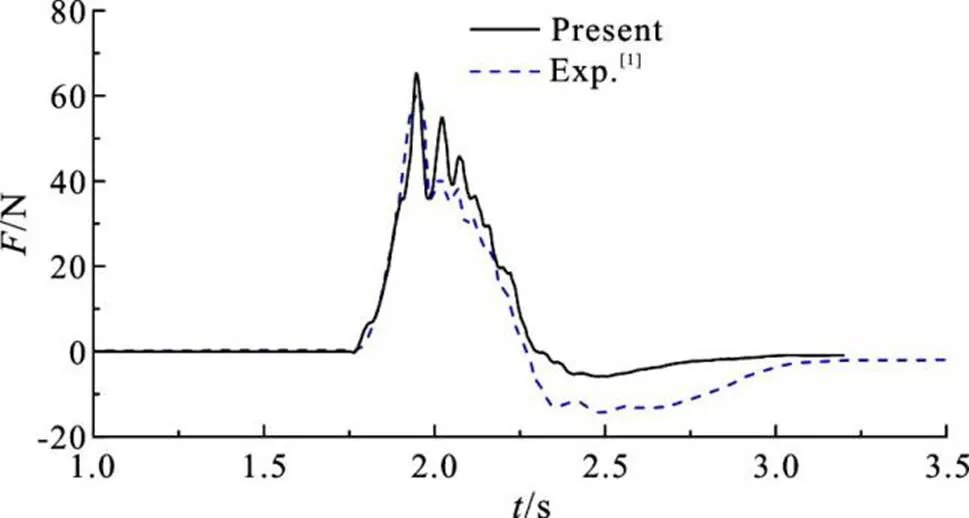
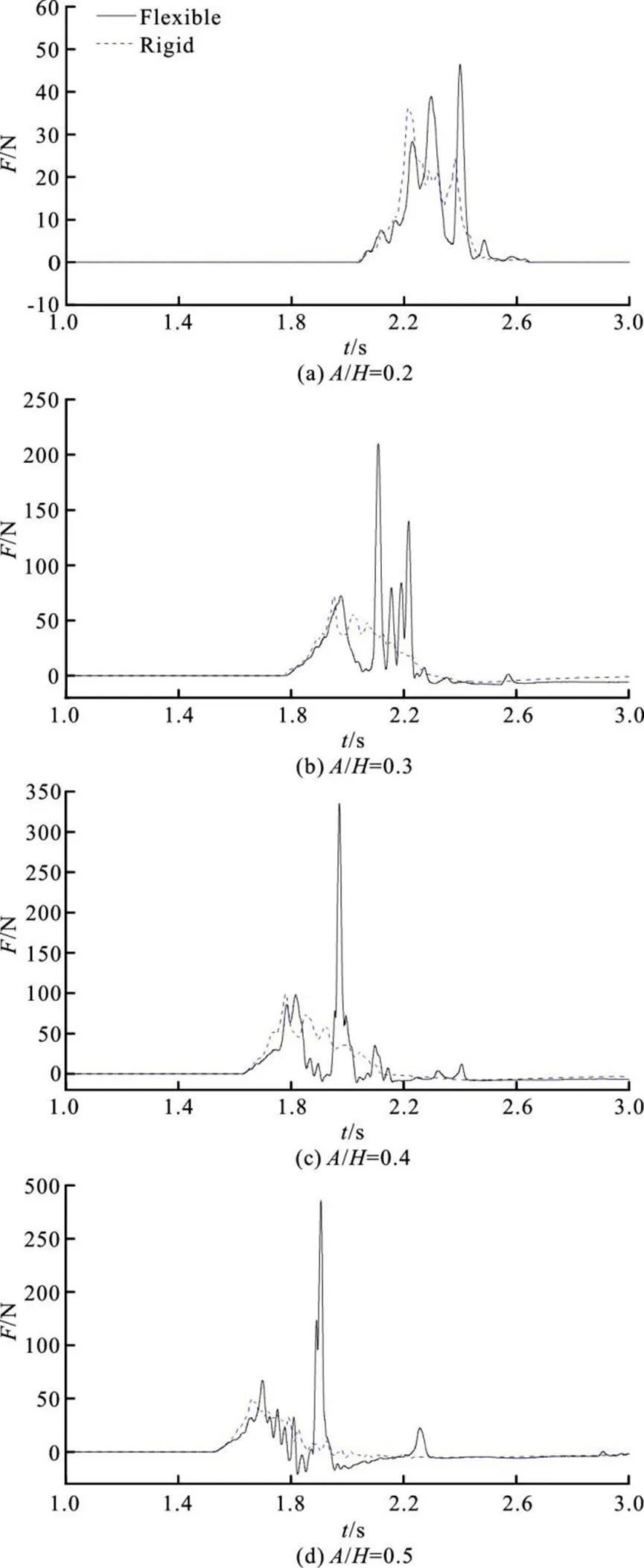
Fig. 4 Slamming force history on plate (, )

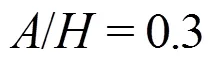
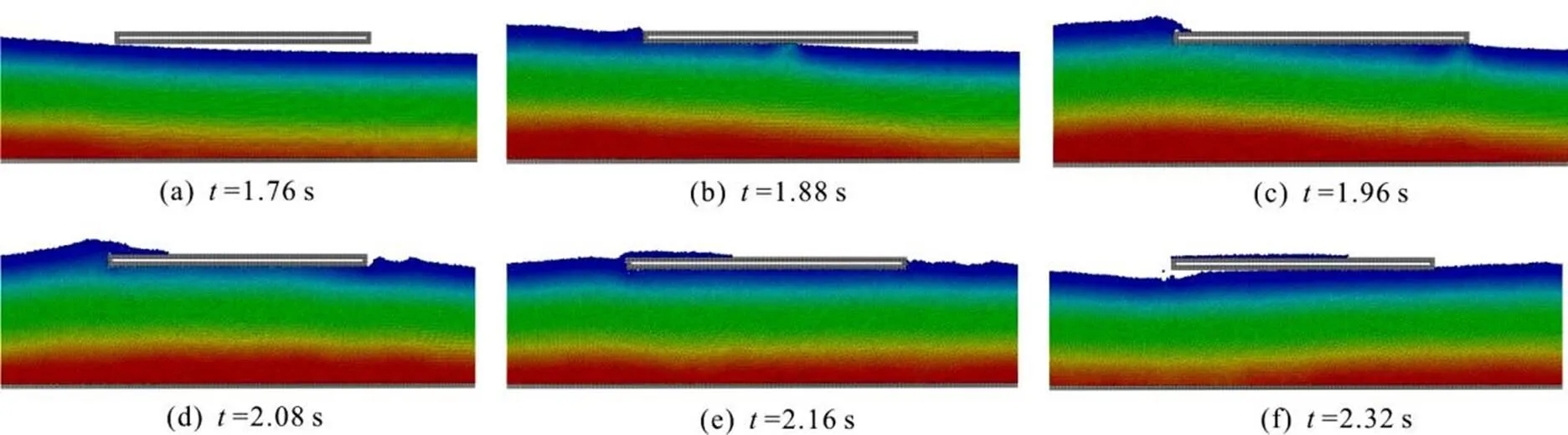
Fig. 5 (Color online) Snapshots of the simulation (,, rigid plate)

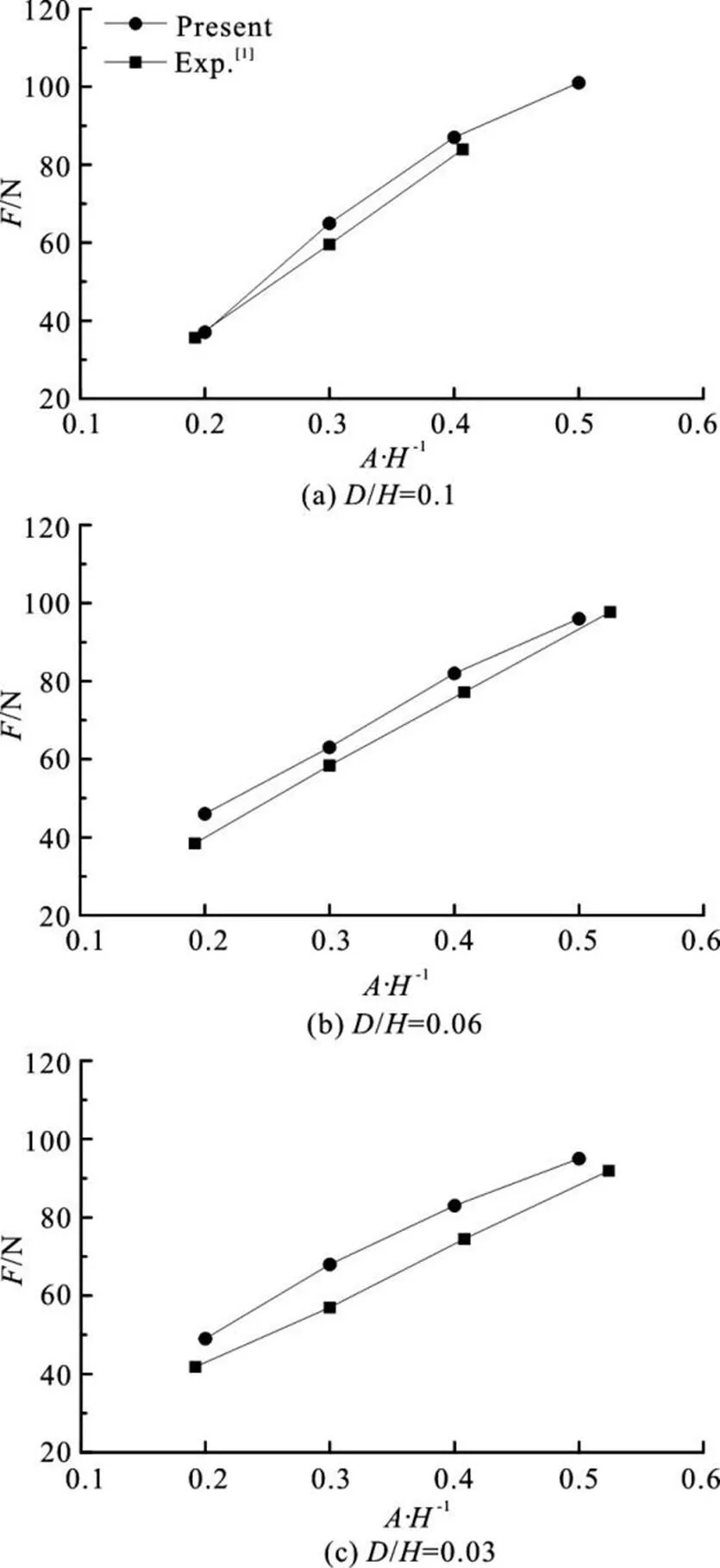
Fig. 6The maximum slamming forces on the plate

To investigate the effects of the wave amplitude and plate elevation on the wave-induced slamming force, the maximum value of the slamming force history in each case is collected. The comparison of the computed and experimental result is shown in Fig. 6. It can be seen that the slamming force on the plate is in proportion to the wave amplitude. However the maxi- mum slamming forces in the cases of different eleva- tion are close to each other, which indicate that the maximum slamming force is not as sensitive to the plate elevation as to the wave amplitude. Although the comparison shows good agreement, the computed maximum slamming force in each case is higher than the experimental result. It is partly due to the surface elevation resulting from the movement of the piston- type wavemaker. The length of the wave tank is rela- tively short compared with the experimental condition and the effects of the surface elevation cannot be neglected.

2.3 Interaction between waves and an elastic plate

To study the effects of structural flexibility on the slamming force, the simulation of the solitary wave interacting with an elastic plate is conducted in this sub-section. The present FSI solver employed has proved to be reliable in our previous research[18, 21, 29]. The setup of the wave amplitude and plate elevation is identical to that in the former subsection, which is shown in Table 2. However, the former rigid plate is replaced by an elastic plate with its ends clamped. The 2-D plate is divided into 152 planar beam elements in the structure analysis. The fluid parameter is the same as the one in the former simulations, which is shown in Table 1. The structural parameter is shown in Table 3.

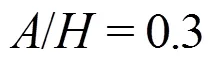
Table3Computational parameters for FEM

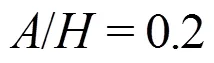
3. Conclusions

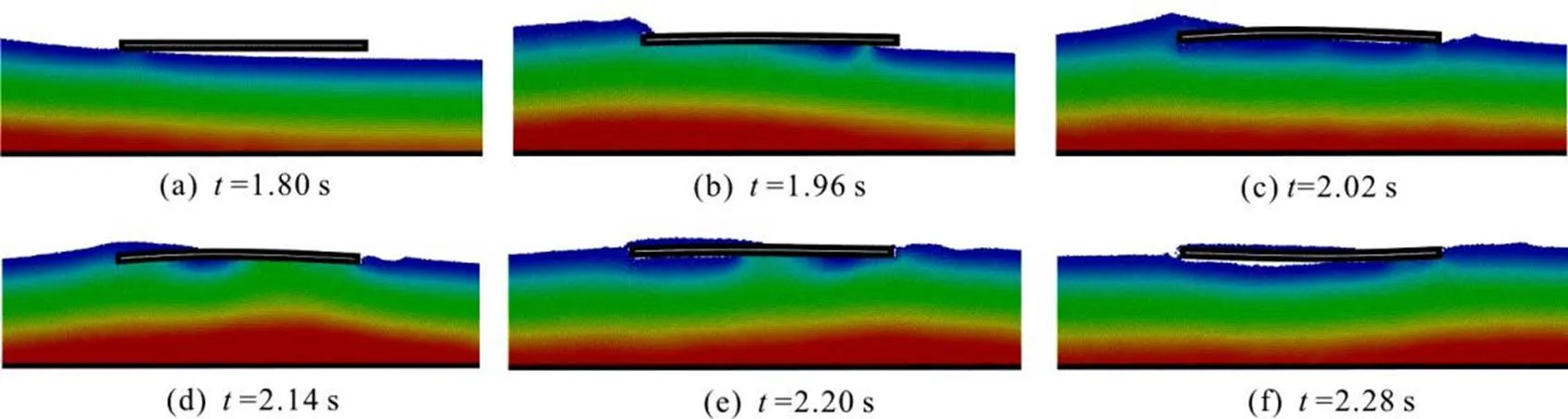
Fig. 8 (Color online) Snapshots of the wave-plate interaction (,,flexible plate)

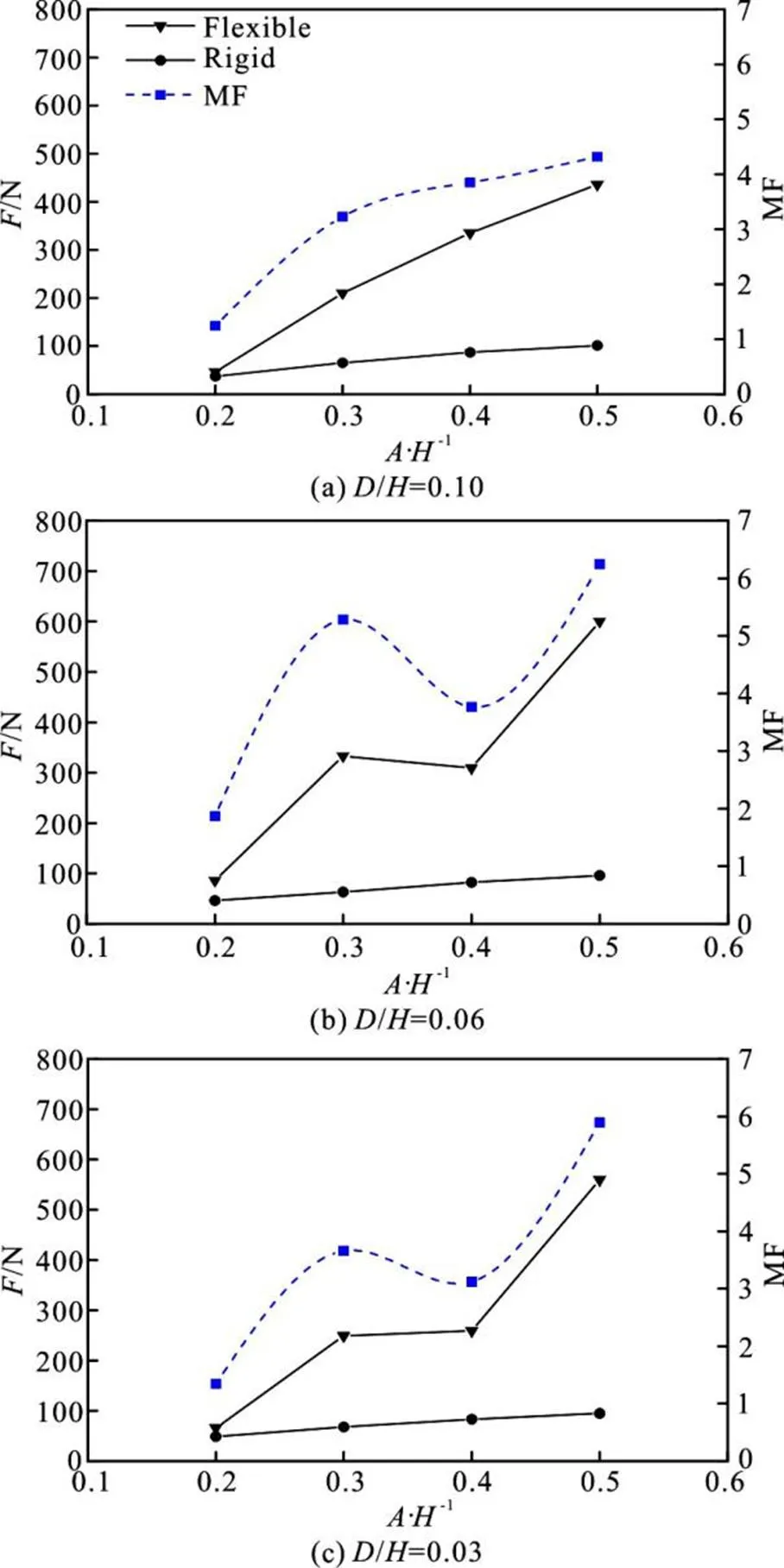
Fig.9(Color online)Themaximumslammingforcesandthe MF

Acknowledgements

This work was supported by the Chang Jiang ScholarsProgram(GrantNo.T2014099),the Shanghai Excellent Academic Leaders Program (Grant No. 17XD1402300), the Program for Professor of Special Appointment (Eastern Scholar) at Shanghai Institu- tions of Higher Learning (Grant No. 2013022), the Innovative Special Project of Numerical Tank of Ministry of Industry and Information Technology of China(GrantNo.2016-23/09)andtheLloyd’s Register Foundation for Doctoral Candidate, to which the authors are most grateful.

[1] Seiffert B., Hayatdavoodi M., Ertekin R. C. Experiments and computations of solitary-wave forces on a coastal- bridge deck. Part I: Flat plate [J]., 2014, 88: 194-209.

[2] Greco M., Colicchio G., Faltinsen O. M. Bottom slam- ming for a very large floating structure: coupled global and slamming analyses [J]., 2009, 25(2): 420-430.

[3] Abrate S. Hull Slamming [J]., 2011, 64(6): 060803.

[4] Liu X., Sakai S. Time domain analysis on the dynamic response of a flexible floating structure to waves [J]., 2002, 128(1): 48-56.

[5] Korobkin A. A., Khabakhpasheva T. I. Regular wave impact onto an elastic plate [J]., 2006, 55(1-4): 127-150.

[6] Liao K., Hu C. A coupled FDM-FEM method for free surface flow interaction with thin elastic plate [J]., 2013, 18(1): 1-11.

[7] Zhang A. M., Sun P. N., Ming F. R. et al. Smoothed particle hydrodynamics and its applications in fluid-struc- ture interactions [J]., 2017, 29(2): 187-216.

[8] Lucy L. B. A numerical approach to the testing of the Fission hypothesis [J]., 1977, 82: 1013-1024.

[9] Gingold R. A., MonaghanJ. J. Smoothed particle hydrody- namics: Theory and application to non-spherical stars [J]., 1977,181(3): 375-389.

[10] Koshizuka S., Oka Y. Moving-particle semi-implicit me- thod for fragmentation of incompressible fluid [J]., 1996, 123(3): 421-434.

[11] Liu M. B., Li S. M. On the modeling of viscous income- pressible flows with smoothed particle hydrodynamics [J]., 2016, 28(5): 731-745.

[12] Attaway S. W., Heinstein M. W., Swegle J. W. Coupling of smooth particle hydrodynamics with the finite element method [J]., 1994, 150(2-3): 199-205.

[13] Antoci C., Gallati M., Sibilla S. Numerical simulation of fluid–structure interaction by SPH [J]., 2007, 85(11): 879-890.

[14]Fourey G., Oger G., Le Touzé D. et al. Violent fluid- structure interaction simulations using a coupled SPH/ FEM method [J]., 2010, 10(1): 012041.

[15] Yang Q., Jones V., McCue L. Free-surface flow interac- tions with deformable structures using an SPH-FEM model [J]., 2012, 55(15): 136-147.

[16] Sun Z., Djidjeli K., Xing J. et al.Coupled MPS-modal su- perposition method for 2D nonlinear fluid-structure interaction problems with free surface [J]., 2016, 61: 295-323.

[17] Lee C. J. K., Noguchi H., Koshizuka S. Fluid–shell struc- ture interaction analysis by coupled particle and finite element method [J]., 2007, 85(11): 688-697.

[18]Rao C., Zhang Y., Wan D. Numerical simulation of the solitary wave interacting with an elastic structure using MPS-FEM coupled method [J]., 2017, 16: 1-10.

[19] Zhang Y., Chen X., Wan D. An MPS-FEM coupled me- thod for the comparative study of liquid sloshing flows interacting with rigid and elastic baffles [J]., 2016, 37(12): 1359-1377.

[20]Zhang Y., Tang Z., Wan D. Numerical investigations of waves interacting with free rolling body by modified MPS method [J]., 2016, 13(4): 1641013.

[21] Zhang Y., Wan D. Numerical study of interactions bet- ween waves and free rolling body by IMPS method [J]., 2017, 155: 124-133.

[22] Mitsume N., Yoshimura S., Murotani K. et al. Improved MPS-FE fluid-structure interaction coupled method with MPS polygon wall boundary model [J]., 2014, 101(4): 229-247.

[23]Hwang S. C., Khayyer A., Gotoh H. et al. Development of a fully Lagrangian MPS-based coupled method for simu- lation of fluid-structure interaction problems [J]., 2014, 50(2): 497-511.

[24] Zhang Y., Wan D. Apply MPS method to simulate liquid sloshing in LNG tank [J]., 2012, 29(12): 1843-1857.

[25] Tanaka M., Masunaga T. Stabilization and smoothing of pressure in MPS method by quasi-compressibility [J]., 2010, 229(11): 4279-4290.

[26] Lee B. H., Park J. C., Kim M. H.et al. Step-by-stepim- provement of MPS method in simulating violent free-sur- facemotions and impact-loads [J]., 2011, 200(9-12): 1113-1125.

[27] Iura M., Atluri S. N. Dynamic analysis of planar flexible beams with finite rotations by using inertial and rotating frames [J]., 1995, 55(3): 453-462.

[28] Hsiao K. M., Lin J. Y., Lin W. Y. A consistent co-rota- tional finite element formulation for geometrically nonlinear dynamic analysis of 3-D beams [J]., 1999, 169(1-2): 1-18.

[29] Rao C., Zhang Y., Wan D. FSI analysis of solitary wave interacting with horizontal flexible plate by MPS-FEM method [C]., San Francisco, California, USA, 2017, 263-272.

[30]Goring D. G. Tsunamis-the propagation of long waves onto a shelf [D]. Doctoral Thesis, Pasadena, California, USA: California Institute of Technology, 1978.

(October 22, 2017, Accepted November 22, 2017)

©China Ship Scientific Research Center 2018

* Project supported by the National Natural Science Foun- dation of China (Grant Nos. 51490675, 11432009, 51579145 and 51379125).

Cheng-ping Rao (1995-), Male, Master Candidate,

E-mail: rao199547@sjtu.edu.cn

De-cheng Wan,

E-mail:dcwan@sjtu.edu.cn