Influence of upstream disturbance on the draft-tube flow of Francis turbine under part-load conditions *
Ting Chen(陈婷), Xianghao Zheng(郑祥豪),Yu-ning Zhang, 4, 5(张宇宁) ,Shengcai Li
Influence of upstream disturbance on the draft-tube flow of Francis turbine under part-load conditions*
Ting Chen1, 2, 3(陈婷), Xianghao Zheng1(郑祥豪),Yu-ning Zhang1, 4, 5(张宇宁) ,Shengcai Li3
1.2.3.4.5.
Owing to the part-load operations for the enhancement of grid flexibility, the Francis turbine often suffers from severe low-frequency and large-amplitude hydraulic instability, which is mostly pertinent to the highly unsteady swirling vortex rope in the draft tube. The influence of disturbances in the upstream (e.g., large-scale vortex structures in the spiral casing) on the draft-tube vortex flow is not well understood yet. In the present paper, the influence of the upstream disturbances on the vortical flow in the draft tube is studied based on the vortex identification method and the analysis of several important parameters (e.g., the swirl number and the velocity profile). For a small guide vane opening (representing the part-load condition), the vortices triggered in the spiral casing propagate downstream and significantly affect the swirling vortex-rope precession in the draft tube, leading to the changes of the intensity and the processional frequency of the swirling vortex rope. When the guide vane opening approaches the optimum one (representing the full-load condition), the upstream disturbance becomes weaker and thus its influences on the downstream flow are very limited.
Francis turbine, vortex identification method, instability, vortex rope, part-load condition, swirl number
Introduction
The Francis turbines are widely applied for im- proving the stability and the flexibility of the power system due to its rapid load adjustment ability to fit the grid load variations (e.g., those induced by the massive entrance of the wind energy[1]). Although the pumped hydro energy storage power plants (PHESPPs) are also widely used in China, their utilization hours are quite limited due the high economic costs and the severe flow-induced unstable phenomenon (e.g., the rotating stall[2]and the significant part-load pressure fluctuation[3]). However, for the load adjustment, the Francis turbine is still quite attractive in terms of its capacities (e.g. over 1 000 MW under the full-load condition) and the low price.
When the Francis turbine is operated at a part load, an extremely complicated flow environment will be generated, leading to various kinds of vortical flows[4, 5](e.g., the complex vortex rope and the inter- blade vortices). It is well known that under certain part-load conditions, a highly unstable vortex-rope precession occurs in the draft tube, leading to severe hydrodynamic instabilities (usually in the low-fre- quency range of the frequency spectrum) in the Francis turbine[6-8]. As commonly recognized, the runner blades are designed according to the optimal operational condition to rectify the rotating fluid (i.e., in ideally swirl-free state at the outlet of runner) toward the axial direction. Under part-load conditions, a swirl flow exists in the cone section of the draft tube, and is manifested in the whole draft tube through the vortex breakdown and the interactions with the sepa- rated elbow flow. It could become further signifi- cantly complicated by the presence of the cavita- tion[9-11]. The consequent pressure fluctuations with large amplitudes (mostly in the low-frequency range) occur throughout the entire turbine system, causing resonances at some eigenfrequencies of the flow system. Therefore, this complex swirling flow in the draft tube often poses a great threat to the safety of the whole system[12].
The underlying mechanism of the draft-tube ins- tabilities is closely related to the vortex breakdown[13]. Although the vortex breakdown in the swirling flow is extensively studied for decades[14-16], it is still not fully understood because this problem is very complicated owing to many interferential factors. For example, the flow entering the draft tube is far from steady and symmetric due to the rotor-stator interactions. Speci- fically, for certain types of Francis turbines, the entering flow in the draft tube is further complicated by the equipped guide plate in the spiral casing[17-19]. The draft-tube flow was intensively investigated[20, 21], while the upstream disturbances were generally ignored because they are usually of much smaller scales (compared with those of the draft-tube vortical flow). Thus they do not resonate with the low-fre- quency modes of the vortex ropes. However, as shown in the present paper, the instabilities caused by the guide plate might serve as a simulative resource in the upstream and their resonance effects with the vortical flow in the draft tube under the part-load conditions are investigated. In our previous work[19], the basic features of the swirling flow inside the turbine (e.g., the spiral casing and the draft tube) were identified based on the analysis of the streamlines and the time- dependent contours of the vortex rope. In the present paper, a more quantitative discussions will be given with the aid of the vortex identification methods and the swirl number.

1. Research methods
1.1 Geometrical model and numerical method
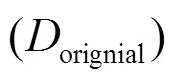
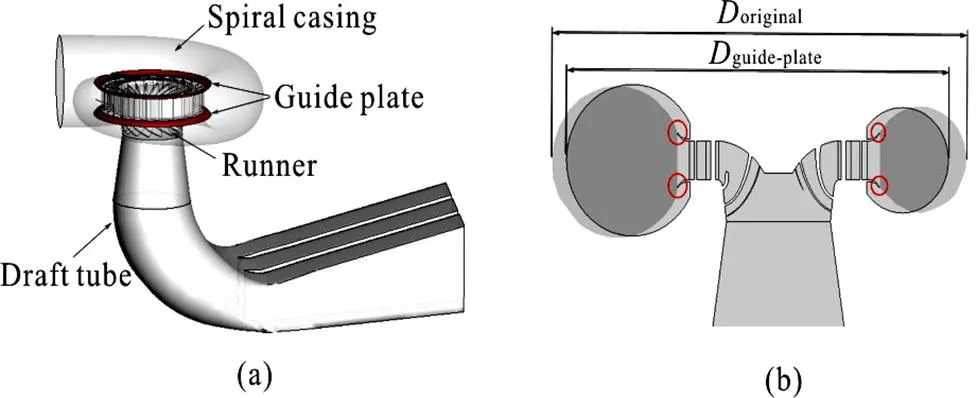
Fig.1 (Color online) A schematic view of the present prototype Francis turbine model. (a) the whole model with the guide plate marked by red color, (b) illustration of size reduction by the guide plate. In the figure, de- notes the original diameter of the spiral casing and denotes the reduced diameter by moving the spiral casing inwards while leaving the butterfly edge of the stay ring as it used to be
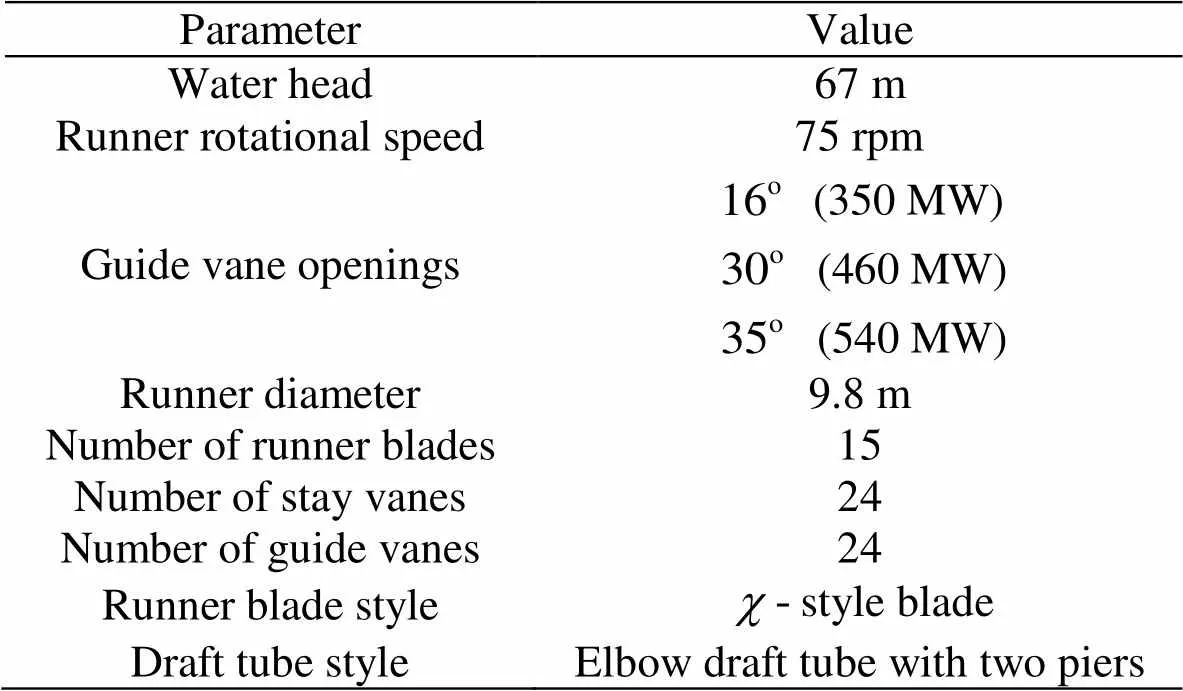
Table1Parameters for the simulated models
1.2 Vortex identification method

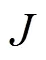
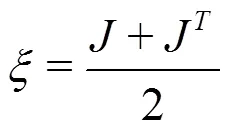
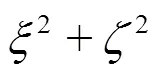
2. Results and discussions
2.1 Vortex patterns in the draft tube for guide vane opening of


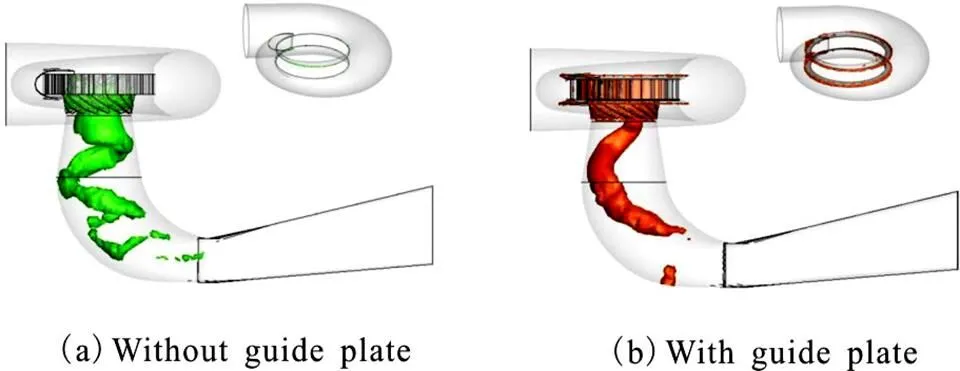
Fig.3 (Color online) Vortex patterns visualized by iso-surfaces of in the whole turbine flow. The guide vane opening is

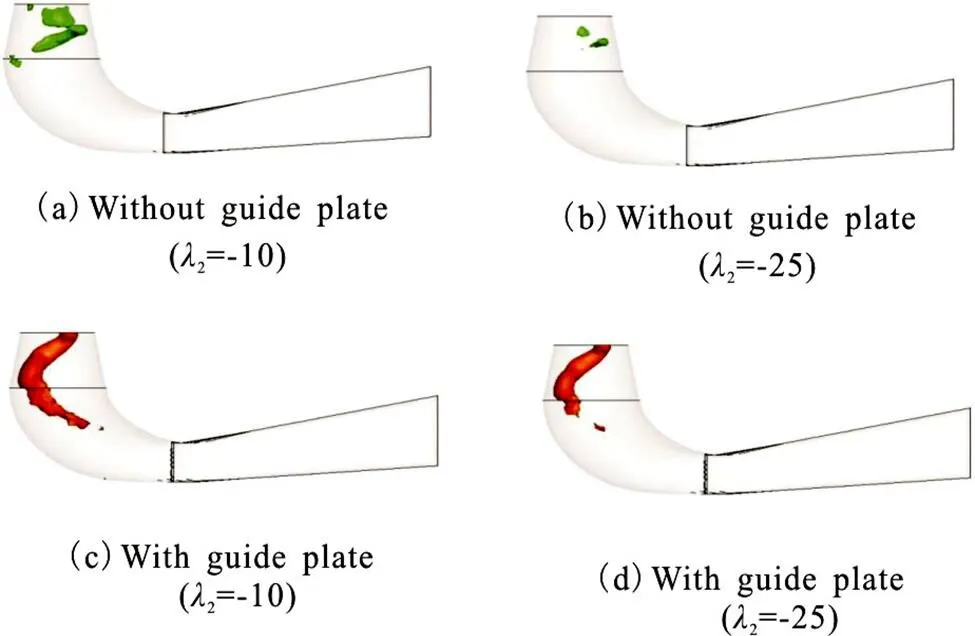
Fig.4 (Color online) Comparison of vortex structures in the draft tube visualized by different values of iso- surfaces. The guide vane opening is
2.2 Vortices triggered by the guide plate
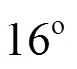
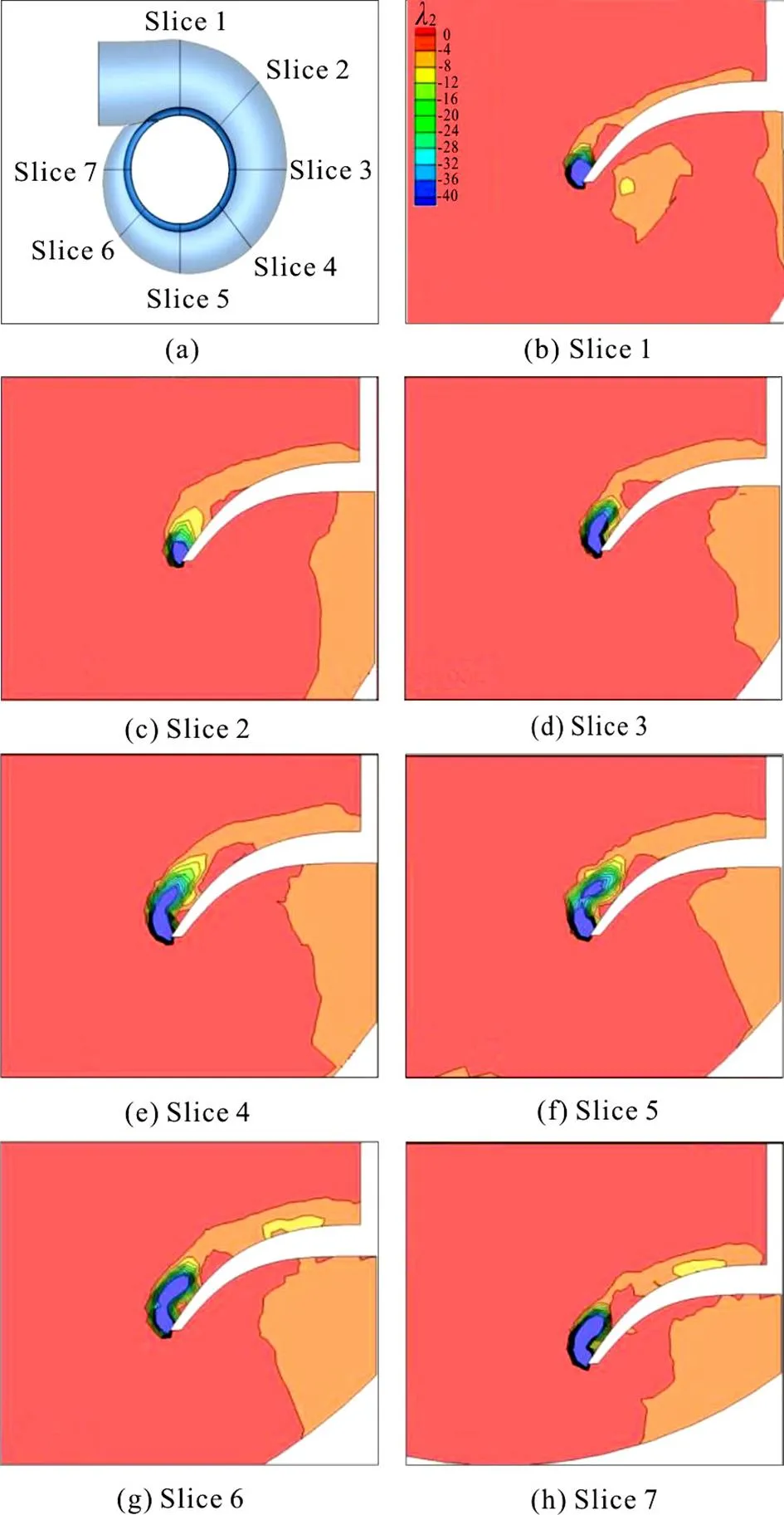
Fig.5 (Color online) Indication of disturbances caused by the guide plate. (a) shows the definitions of seven slices of spiral casing in the circumferential direction, (b)-(h) show contours of these seven slices. Blue and red colors correspond to the minimum and maximum values, respectively. The guide vane opening is

Fig. 6 (Color online) Indication of disturbances caused by the guide plate. (a)-(d) show the contours of four slices of spiral casing as defined in Fig. 5(a). Blue and red colors correspond to the minimum and maximum values, respectively. The guide vane opening is

2.3 Vortex structures for guide vane openings of and

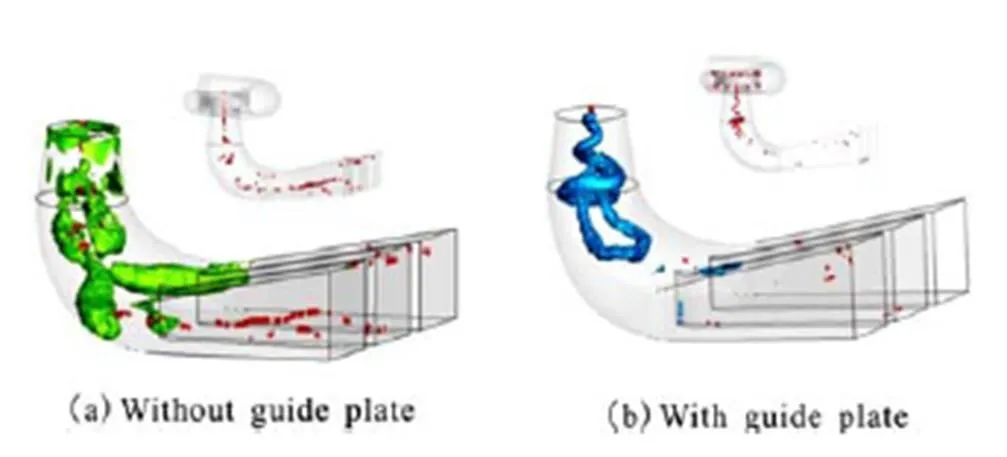
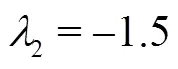

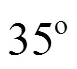
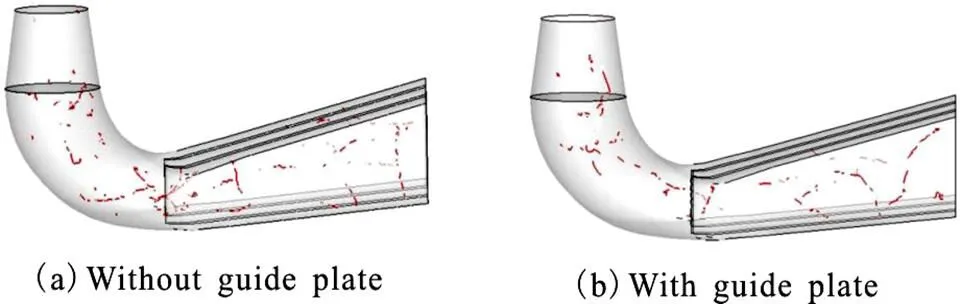
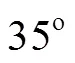
Under the part-load conditions, the swirl flow in the cone section of the draft tube raises the rotational momentum in the flow when it leaves the runner. The onset of the vortex breakdown in the draft tube is correlated with a dimensionless parameter (the swirl number, represented by) such as[11]
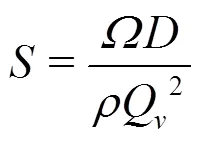

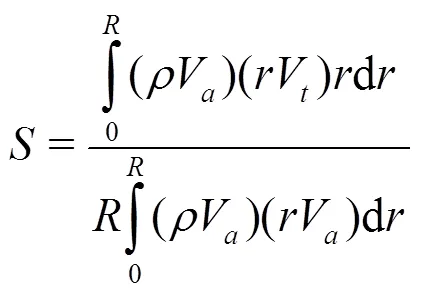
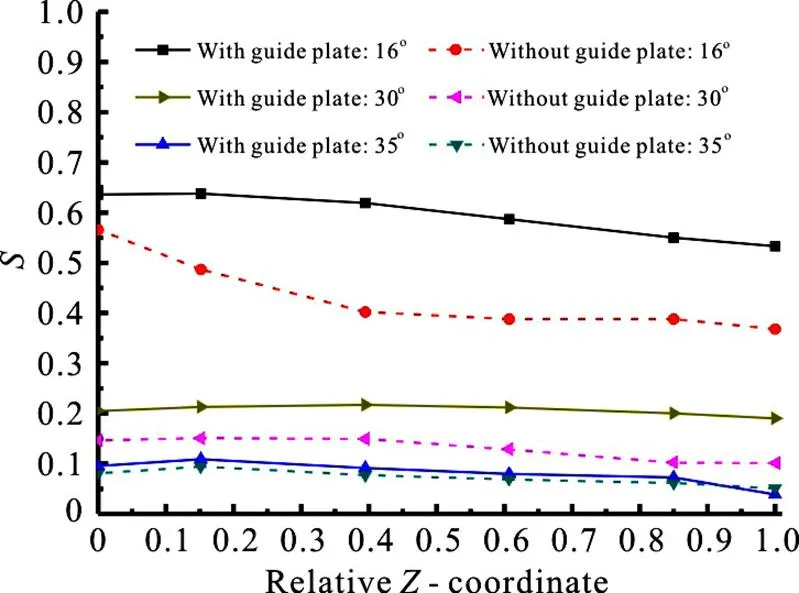
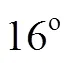
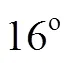
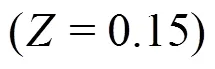
3. Limitations
The results obtained in the present paper explain the physics of the phenomena reasonably well. How- ever, the methods adopted for the analysis have some inherent limitations, which will be briefly discussed as follows:
(1)The vortex-core extraction technique is based on the algorithm that automatically locates the center of swirling flow in the vector fields. With this method, satisfactory results can be obtained under most circu- mstances, particularly, for strong swirl flows with large swirl velocity. However, to some extent, the accuracy of this method depends on the intensity of the vortices and the grid size. For example, the vortex core may not be predicted well in very weak swirl flows. Moreover, in some cases, the generated vortex core is not continuous owing to the non-uniform mesh distributions.
(3) One of the negative effects of the addition of the guide plate is the triggered cavitation damage on the guide vanes as spotted in our previous studies. Due to the limited spaces, the present model does not involve the cavitation simulation. The cavitation phenomenon is quite complex in the hydroturbines because many highly complex effects (e.g., the cavi- tation resonance, the bubble-bubble interactions[24], the chaos[25]and the combination resonances[26]) could be involved together with a prominent mass transfer[27]and the surface instability[28]. Specifically, the pres- sure fluctuation could be significantly altered by the presence of cavitation bubbles[29](e.g., in terms of attenuation). For some Francis turbines in China (e.g., in Yellow river), the silt (e.g., particles) is of high concentration in the water and the cavitation-particle interaction will further deteriorate the flow conditions inside the turbine[30](e.g., generations of more vortices).
4. Conclusions
This paper investigates the influences of the ups- tream disturbances on the instabilities of the draft tube in the prototype Francis turbine. Under part-load con- ditions, it is found that the guide-plate induced vortex structure could significantly affect the unstable flow inside the turbine by resonating with the vortex struc- tures in the draft tube. The draft tube surge and the vortex rope are extensively discussed with an emp- hasis on the modification of the velocity profiles, the increase of the swirling number, and the generation of a strong vortex. Under full-load conditions, the above interactions between the upstream and the down- stream are limited. Usually, the influences of the upstream disturbance on the downstream instabilities are neglected during the design stage. However, the interactions between the upstream and the down- stream could be very strong and the involved mecha- nism is very complicated, highly depending on the operational conditions. The present findings highlight this issue from the technical point of view and suggest to pay serious attention on the potential newly-intro- duced unstable fluid flow especially under the part- load conditions. The present methodology and an- alysis are not only applicable to the Francis turbines here but also could be extended to the other kinds of fluid machinery (e.g., pumps[31, 32]and pump tur- bines[33-35]).
Due to the rapid increase of the equipped capa- city of the power stations in China, there are many serious hydro energy rejection problems. As a result, many hydro turbines are forced to be operated under (very low) part-load conditions. This problem is quite serious in Sichuan and Yunnan provinces in China. Currently, many industries with a high-level electric energy consumption (e.g., the coal chemical enginee- ring[36, 37]and the electric vehicles) are developed to solve the dilemma. This trend further strengths the importance of the research of the part-load condition investigated here.
Acknowledgements
This work was suppored by the Fundamental Research Funds for the Central Universities (Grant No. JB2015RCY04), the Open Research Fund Program of Key Laboratory of Fluid and Power Machinery, Ministry of Education, Xihua University (Grant No. szjj-2017-100-1-003), the Open Foundation of Na- tional Research Center of Pumps, Jiangsu University (Grant No. NRCP201601) and the Open Research Fund Program of State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University (Grant No. LAPS16014).
[1] Zhang Y., Tang N., Niu Y. et al. Wind energy rejection in China: Current status, reasons and perspectives [J]., 2016, 66(12): 322-344.
[2] Zhang Y., Zhang Y., Wu Y. A review of rotating stall in reversible pump turbine [J]., 2017, 231(7): 1181-1204.
[3] Zhang Y., Chen T., Li J. et al. Experimental study of load variations on pressure fluctuations in a prototype rever- sible pump turbine in generating mode [J]., 2017, 139(7): 074501.
[4] Escudier M. Confined vortices in flow machinery [J]., 1987, 19(1): 27-52.
[5] Dörfler P., Sick M., Coutu A. Flow-induced pulsation and vibration in hydroelectric machinery: Engineer’s guide- book for planning, design and troubleshooting [M]. London, UK: Springer-Verlag, 2013.
[6] Wu Y., Li S., Liu S. et al. Vibration of hydraulic ma- chinery [M]. Dordrecht, The Netherlands: Springer Science+Business Media, 2013.
[7] Foroutan H., Yavuzkurt S. An axisymmetric model for draft tube flow at partial load [J]., 2016, 28(2): 195-205.
[8] Susan-Resiga R., Muntean S., Hasmatuchi V. et al. Analy- sis and prevention of vortex breakdown in the simplified discharge cone of a Francis turbine [J]., 2010, 132(5): 051102.
[9] Li S. Cavitation of hydraulic machinery [M]. London, UK: Imperial College Press, 2000.
[10]Escaler X., Egusquiza E., Farhat M. et al. Detection of cavitation in hydraulic turbines [J]., 2006, 20(4): 983-1007.
[11] Li S. Tiny bubbles challenge giant turbines: Three Gorges puzzle [J]., 2015, 5(5): 20150020.
[12]Cassidy J., Falvey H. Observations of unsteady flow arising after vortex breakdown [J]., 1970, 41: 727-736.
[13] Nishi M. Surging characteristics of conical and elbow type draft tubes [C]., Stirling, UK, 1984, 272-283.
[14] Alekseenko S., Kuibin P., Okulov V. et al. Helical vortices in swirl flow [J]., 1999, 382: 195-243.
[15] Benjamin T. Theory of the vortex breakdown phenomenon [J]., 1962, 14: 593-629.
[16] Anup K., Lee Y., Thapa B. CFD study on prediction of vortex shedding in draft tube of Francis turbine and vortex control techniques [J]., 2016, 86(2): 1406-1421.
[17] Chen T., Li S. Numerical investigation of guide-plate in- duced pressure fluctuations on guide vanes of three gorges turbines [J]., 2011, 133(6): 061101.
[18] Chen T. First step of verification of Liʼs hypothesis: iden- tification of a new vortex structure induced by guide-plate in three gorges turbines [D]. Doctoral Thesis, Coventry, UK: University of Warwick, 2014.
[19] Chen T., Zhang Y.,Li S. Instability of large-scale proto- type Francis turbines of Three Gorges power station at part load [J]., 2016, 230(7): 619-632.
[20] Zhang R., Mao F., Wu J. et al. Characteristics and control of the draft-tube flow in part-load Francis turbine [J]., 2009, 131(2): 021101.
[21] Galván S., Reggio M., Guibault F. Numerical optimization of the inlet velocity profile ingested by the conical draft tube of a hydraulic turbine [J]., 2015, 137(7): 071102.
[22] Zhang Y., Liu K., Xian H. et al. A review of methods for vortex identification in hydroturbines [J]., 2018, 81(1): 1269-1285.
[23] Jeong J., Hussain F. On the identification of a vortex [J].,1995, 285: 69-94.
[24] Zhang Y., Zhang Y., Li S. The secondary Bjerknes force between two gas bubbles under dual-frequency acoustic excitation [J]., 2016, 29: 129-145.
[25] Zhang Y., Zhang Y. Chaotic oscillations of gas bubbles under dual-frequency acoustic excitation [J]., 2018, 40 (Part B): 151-157.
[26] Zhang Y., Zhang Y., Li S. Combination and simultaneous resonances of gas bubbles oscillating in liquids under dual-frequency acoustic excitation [J]., 2017, 35 (Part A): 431-439.
[27] Zhang Y., Gao Y., Guo Z. et al. Effects of mass transfer on damping mechanisms of vapor bubbles oscillating in liquids [J]., 2018, 40 (Part A): 120-127.
[28] Zhang Y., Gao Y., Du X. Stability mechanisms of oscilla- ting vapor bubbles in acoustic fields [J]., 2018, 40 (Part A): 808-814.
[29] Zhang Y., Guo Z., Gao Y. et al. Acoustic wave propa- gation in bubbly flow with gas, vapor or their mixtures [J].. 2017, 40 (Part B): 40-45.
[30] Zhang Y., Zhang Y., Qian Z. et al. A review of micros- copic interactions between cavitation bubbles and particles in silt-laden flow [J]., 2016, 56: 303-318.
[31]Tan L., Yu Z., Xu Y. et al. Role of blade rotational angle on energy performance and pressure fluctuation of a mixed-flow pump [J]., 2017, 231(3): 227-238.
[32] Tan L., Zhu B., Cao S. et al. Numerical simulation of un- steady cavitation flow in a centrifugal pump at off-design conditions [J]., 2014, 228(11): 1994-2006.
[33] Li J. W., Zhang Y. N., Liu K. H. et al. Numerical simu- lation of hydraulic force on the impeller of reversible pump turbines in generating mode [J]., 2017, 29(4): 603-609.
[34] Li D., Wang H., Qin Y. et al. Numerical simulation of hysteresis characteristic in the hump region of a pump- turbine model [J]., 2018, 115: 433-447.
[35] Li D., Wang H., Qin Y. et al. Entropy production analysis of hysteresis characteristic of a pump-turbine model [J]., 2017, 149: 175-191.
[36] Gao D., Qiu X., Zhang Y. et al. Life cycle analysis of coal based methanol-to-olefins processes in China [J]., 2018, 109: 112-118.
[37] Gao D., Ye C., Ren X. et al. Life cycle analysis of direct and indirect coal liquefaction for vehicle power in China [J]., 2018, 169: 42-49.
(July 18, 2016,Accepted October 8, 2016)
©China Ship Scientific Research Center 2018
* Project supported by the National Natural Science Foun- dation of China (Grant No. 51506051).
Ting Chen (1984-), Female, Ph. D.,
Associate Professor, E-mail: chentingemail@163.com
Yu-ning Zhang,
E-mail:y.zhang@ncepu.edu.cn
- 水动力学研究与进展 B辑的其它文章
- Spectral/hp elementmethods:Recent developments,applications, and perspectives *
- Modeling of single film bubble and numerical study of the plateau structure in foam system *
- Numerical study of the wave-induced slamming force on the elastic plate based on MPS-FEM coupled method *
- Gas-liquid flow splitting in T-junction with inclined lateral arm *
- 3-D Lagrangian-based investigations of the time-dependent cloud cavitating flows around a Clark-Y hydrofoil with special emphasis on shedding process analysis *
- The experimental study of hydrodynamic characteristics of the overland flow on a slope with three-dimensional Geomat *

