突发事件下多种信息交互传播的动力机制与调控策略*
王治莹,王伟康
(安徽工业大学 管理科学与工程学院,安徽 马鞍山 243032)
0 引言
近年来,频繁爆发的突发事件(如火灾、干旱、水灾、地震、龙卷风、流行病、饥荒、食品安全和生产事故)给人类造成了巨大的生命和财产损失[1]。同时,多种关于突发事件的信息也往往伴随事件的爆发而快速蔓延,若对此响应不利,可能进一步诱发次生危害。如:2009年,河南杞县利民辐照厂卡源事件发生后,引发了“核泄漏”传言,虽然当地政府通报“安全无事”等消息,但依然导致了民众的恐慌和逃离县城行为;2015年,上海金山居民抵制PX事件中,“高桥石化搬至金山区”和“可能上马PX项目”等消息经由微博、微信快速扩散,虽然金山区政府官方微博发布了“高桥石化关停”和“不会有PX项目”等信息,但民众普遍不信,并制造了静坐、游行和示威等反对活动。鉴于以上情况,研究突发事件下多种信息间的交互动力机制和调控问题具有重要的现实意义。
目前,关于突发事件下多种信息的分类和特点研究,已受到学者们的广泛关注。刘怡君等[2]在以“8·12天津港爆炸事故”为例进行舆情传播规律探索时发现,正面信息以新闻媒体为主导,但影响弱、集中性小,而负面信息主要来源于公众个体,内容多元化;陈业华等[3]在研究公共场所突发事件受灾人群的信息传播时发现,信息扩散具有交互性、多元性、紊乱性、瞬时性和竞争性等特征;武澎等[4]从信息传播系统中的枢纽节点判定角度,探讨了具有社会价值的信息和谣言的传播干预;Ou等[5]分析了信息异质性对不同网络结构中信息传播的影响,发现对于小世界网络,信息异质性的增强不仅会降低其信息传播效率,还会延长其信息传播的生命周期。此外,Zhang等[6]通过借鉴Lotka-Volterra竞争模型,研究了不同社会网络结构中多种信息间的交互传播与演化规律;Wang等[7]通过扩展SIR传染病模型,研究了一种谣言比另一种谣言更具吸引力情况下的共同传播问题;Xie等[8]研究了无标度网络中,两种竞争性舆情信息的传播对不同产品支持率的影响。相比之下,突发事件下单一信息的传播影响因素及其作用机制研究更为普遍,如管理者的压制行为[9]、民众的风险感知[10]和影响力[11]等,可为本文研究突发事件下多种信息的交互传播动力机制提供参考。
总结上述研究成果可以发现:现有研究很少关注到突发事件下多种信息共存情境中的信息交互关系和动力机制;多种信息的交互关系,本质上是群体在面对不同信息时的行为状态转移关系,表现在具有不同行为状态的群体数量的演化,而明晰这种演化规律有助于厘清调控决策的制定要点,但现有研究对此涉及较少;由于多种信息共存情境中每种信息都分别对群体的行为状态进行了划分,因此,多种信息舆论场能够影响不同信息间的群体行为状态转移,而现有研究也缺少对该问题的考虑。为此,综合考虑这些问题,将界定突发事件下多种信息共存情境中“涌现→传播”过程的信息交互关系框架,并建立系统动力学模型,进一步结合基础情景和实验情景仿真,研究决策者关键可控因素的作用机制与调控策略问题。
1 问题描述与研究假设
为了降低研究的复杂性并考虑到研究中的一些不确定因素,给出以下假设:
1)假设1:突发事件下,多种信息可聚类为2类互为异质性或竞争性的信息,即信息A和信息B。突发事件下,多种信息的真伪虽然可在事后确定,但在事发早期难以准确辨别。事实上,各种信息都有特定的来源渠道,不妨将其按照渠道差异,归类为2类互为异质性或竞争性的信息,记为信息A和信息B。信息A代表政府官网、主流媒体和大型门户网站(如:中央电视台、人民日报、中国日报、人民网、新华网和凤凰网等)发布的相对理性和正式的信息;信息B代表新媒体(微博、微信、论坛和贴吧)和人际关系渠道散布的相对非理性和非正式的信息。
2)假设2:将信息的“涌现→传播”过程细分为“信息未知→初步了解→形成立场→产生行为”4个发展阶段,并将群体按其在不同阶段中的行为状态划分为:未知者、已知但无立场者、相信信息A且不传播者、相信信息B且不传播者、信息A传播者、信息B传播者。根据群体的认知特点,可将单一信息情境中,信息发展阶段和群体行为状态的划分思路[12]推广到多种信息的共存情境之中。未知者(Unknown group, UG),即从未接触过信息的群体;已知但无立场者(Known but non-standpoint group, KNG),即已获知信息,但由于无心关注或暂时犹豫而未形成自身立场的群体;相信信息A且不传播者(Trusted but not disseminated group for A, TNG-A)和相信信息B且不传播者(Trusted but not disseminated group for B, TNG-B),即分别指相信信息A和信息B,但尚未产生传播行为的群体;信息A传播者(disseminated group for A, DG-A)和信息B传播者(disseminated group for B, DG-B),即分别指对信息A和信息B具有传播行为的群体。
3)假设3:信息的传播渠道畅通,不同群体间的行为状态转移主要取决于群体自身的选择。本文重点关注信息的“涌现→传播”过程,而由于现实中该过程的演化往往极为迅速,故在此过程中,政府和媒体运营商一般忙于事件信息的发布,而对群体行为的干预更多采取的是监测和预警,不涉及渠道屏蔽,如上文2015年发生的上海金山居民抵制PX事件。
4)假设4:多种信息舆论场的影响力体现在其对不同信息间群体行为状态转移的反馈作用,即信息A(或信息B)舆论场的影响力促使其他群体向TNG-A(或TNG-B)和DG-A(或DG-B)群体转移,同时抑制TNG-A(或TNG-B)和DG-A(或DG-B)群体向其他群体转移。
总结以上,可给出信息A和信息B共存情境中“涌现→传播”过程的信息交互框架,如图1所示,该框架包括群体行为状态转移和信息舆论场反馈作用2个子框架。在群体行为状态转移子框架中,部分UG在获取信息后,短时间内由于无心关注、观望或犹豫而未形成立场,故转化为KNG;随着认知更新和群体间的接触,KNG会以一定概率选择相信信息A或信息B,但受制于形成立场到产生行为间的时间延迟而不会立即传播,即转变为TNG-A或TNG-B;进一步,随着事态发展,TNG-A和TNG-B中部分较为活跃的群体会由于自身利益和好奇心等的驱使而产生传播行为,即转变为DG-A和DG-B;同时,随着信息A与信息B舆论场的反馈作用逐渐体现,加之这2类信息间的竞争性特点,TNG-A和TNG-B会以一定概率相互转化,DG-A和DG-B也可能转变自身立场。在信息舆论场反馈作用子框架中,经由群体行为状态转移子框架所输出的信息A与信息B舆论场,各自的影响力对不同群体间行为状态的转移都具有反馈作用,具体见假设4。
2 模型构建
2.1 相关参数与符号说明
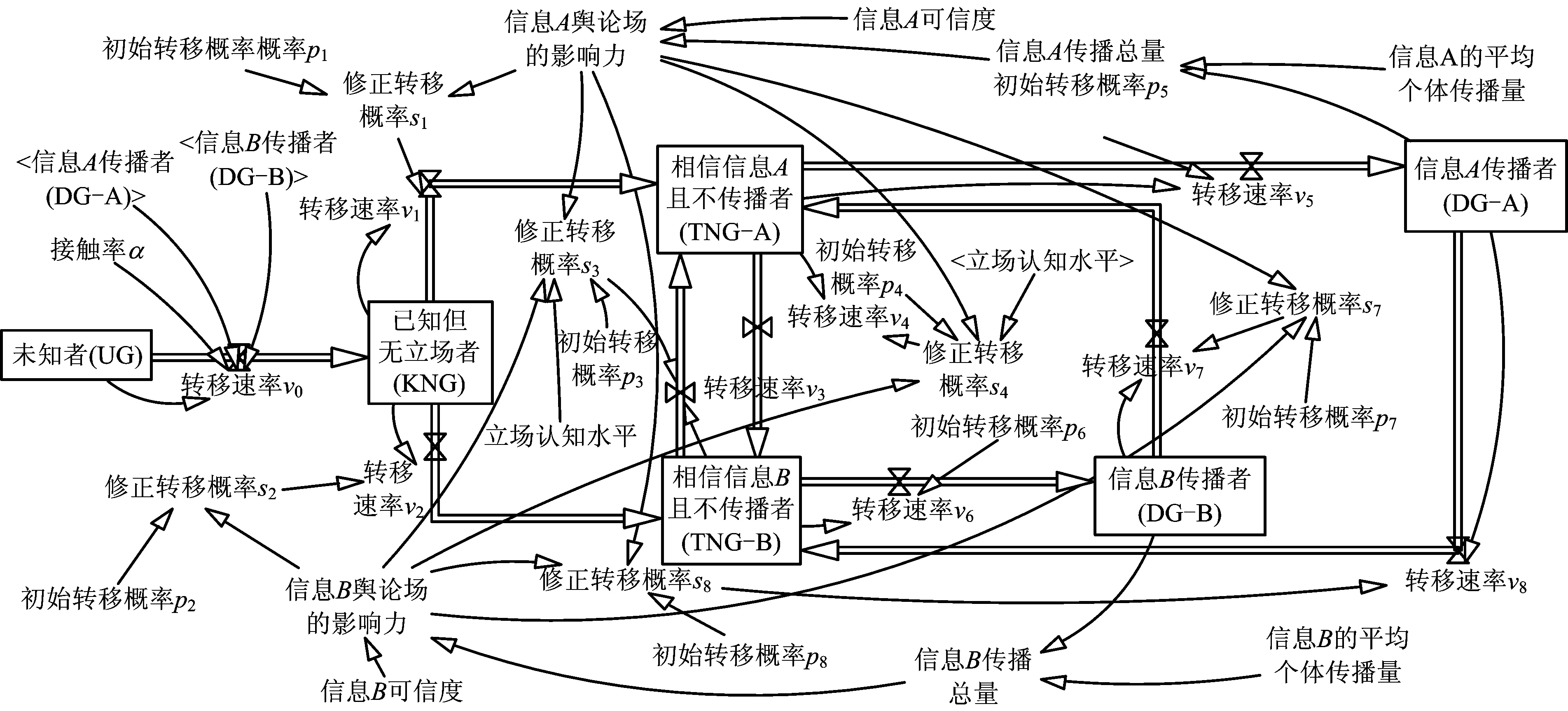
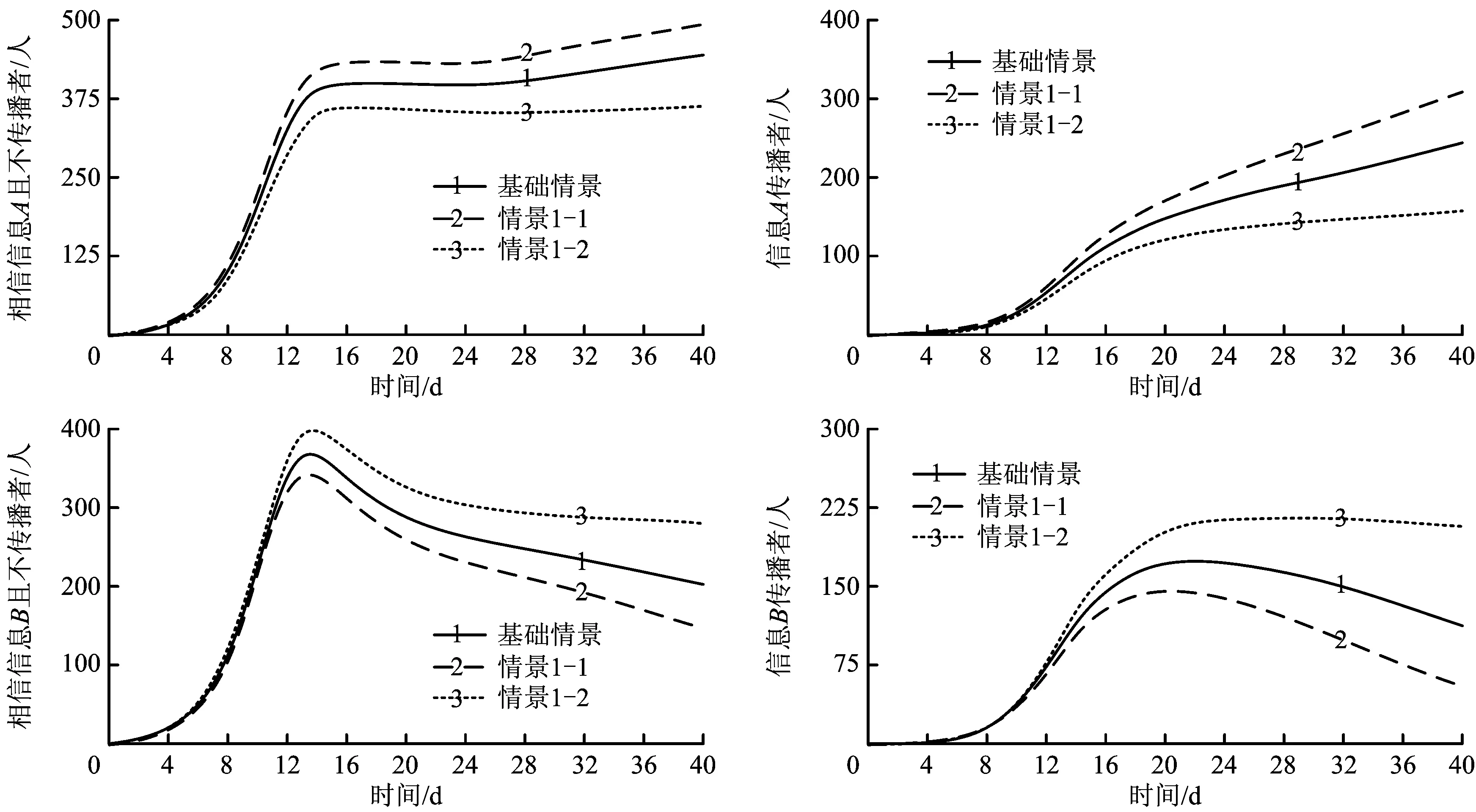
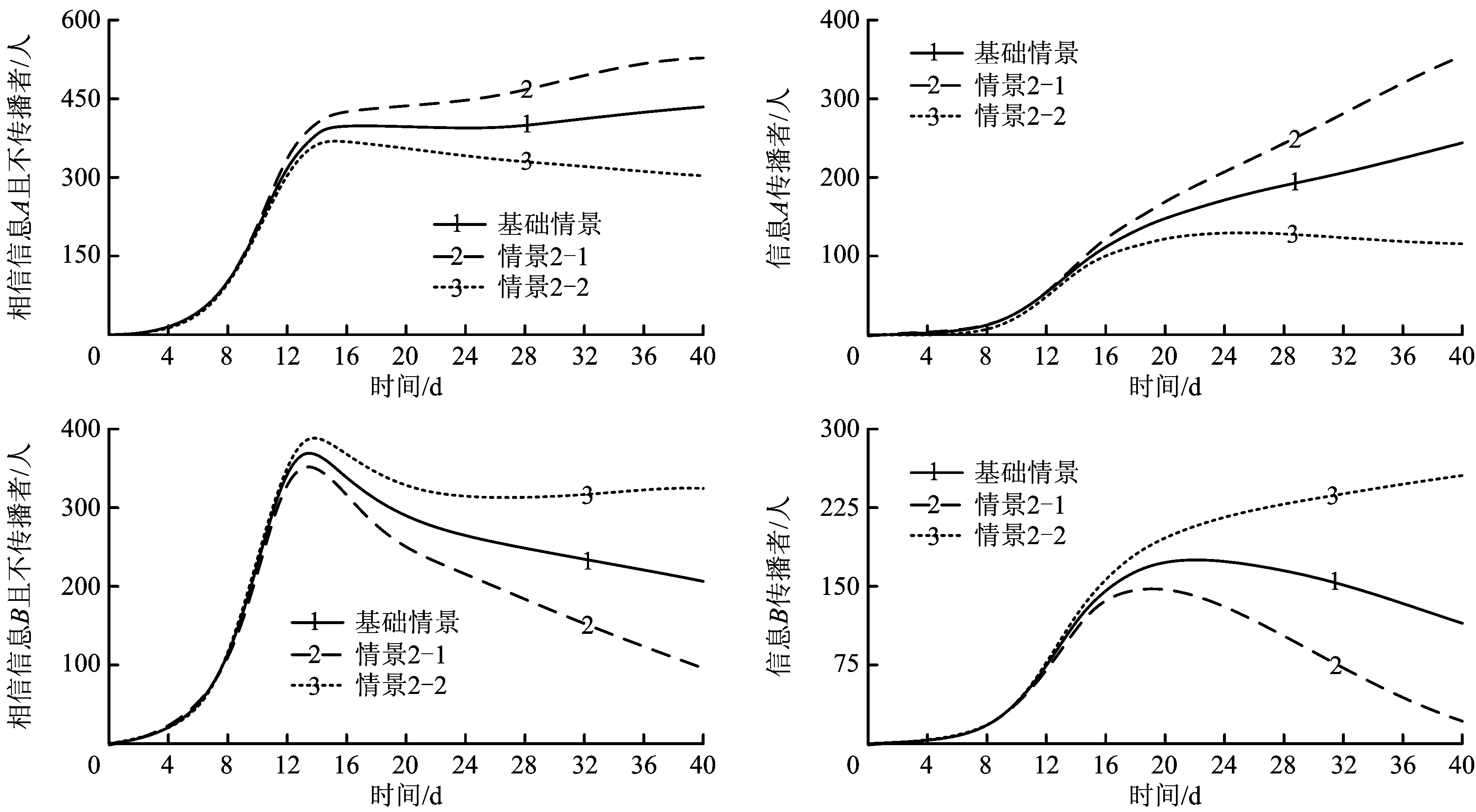
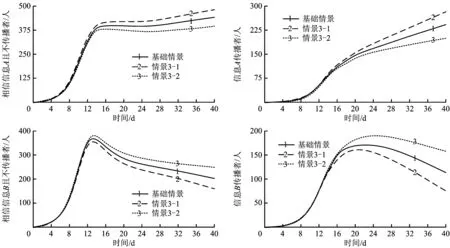
根据以上模型框架和系统边界,给出接触率、初始转移概率(不受舆论场反馈作用影响下的概率)和修正转移概率(受舆论场反馈作用影响下的概率)的定义:α表示UG与传播者(DG-A和DG-B)的接触率;p1和s1分别表示KNG向TNG-A的初始和修正转移概率;p2和s2分别表示KNG向TNG-B的初始和修正转移概率;p3和s3分别表示TNG-B向TNG-A的初始和修正转移概率;p4和s4分别表示TNG-A向TNG-B的初始和修正转移概率;p5表示TNG-A向DG-A的初始转移概率;p6表示TNG-B向DG-B的初始转移概率;p7和s7分别表示DG-B向TNG-A的初始和修正转移概率;p8和s8分别表示DG-A向TNG-B的初始和修正转移概率。其中,α,p1,p2,…,p8,s1,s2,…,s8∈[0,1]。一般情况下,p1 事实上,以解构图1中信息舆论场的反馈作用为切入点,可借助系统动力学理论[13]建立因果回路图,包括信息A舆论场反馈回路和信息B舆论场反馈回路,具体如下: 图2 信息A舆论场的因果回路Fig.2 Causal loop of public opinion field on information A 1)信息A舆论场反馈回路:如图2所示,信息A可信度→信息A舆论场→相信信息A且不传播者(TNG-A)→信息A传播者(DG-A)→信息A传播总量→信息A舆论场。根据假设3,在群体可自由选择其行为状态下,信息A舆论场的影响力大小主要取决于信息A本身的可信度及其传播总量;由假设4可知,信息A舆论场的影响力会促进其他群体向TNG-A和DG-A转移,同时抑制TNG-A和DG-A向其他群体转移,即提高s1,s3和s7,降低s4和s8,从而促进TNG-A和DG-A人数的增加;在一定的信息A平均个体传播量下,DG-A人数的增加必将致使信息A传播总量的增加;而信息A传播总量的增加又会进一步提升信息A舆论场的影响力,由此形成因果回路。 2)信息B舆论场反馈回路:如图3所示。 图3 信息B舆论场的因果回路Fig.3 Causal loop of public opinion field on information B 信息B可信度→信息B舆论场→相信信息B且不传播者(TNG-B)→信息B传播者(DG-B)→信息B传播总量→信息B舆论场。与信息A舆论场反馈回路 不同的是,信息B舆论场的影响力会促进其他群体向TNG-B和DG-B转移,同时抑制TNG-B和DG-B向其他群体转移,即提高s2,s4和s8,降低s3和s7。 需要说明的是,群体在获知信息A和信息B并形成相信其中一类信息的立场后,能够决定其向相信另一类信息立场转变的因素除了这2类信息的舆论场影响力外,更为根本的是其立场的坚定程度。由假设1中信息A和信息B的划分标准可知,群体相信其中一类信息立场的坚定程度实质是其对该类信息传播渠道的相信程度,这主要取决于群体的立场认知水平[14]。即:群体的立场认知水平越高,其相信来自官方渠道的信息A可能性越大,而相信来自民间渠道的信息B可能性越小,故TNG-A向TNG-B的转移概率越低,且TNG-B向TNG-A的转移概率越高。 进一步梳理速率变量(即群体间的转移速率)、状态变量(即不同群体的数量)及辅助变量(即信息A和信息B舆论场反馈回路中的影响因素),借助Vensim软件得到流图,如图4所示。 图4 信息A和信息B共存情境下的流图Fig. 4 Flow diagram under the situation of coexisting of information A and B 模型中的变量计算方法和构造思路如下: 1)群体行为状态转移子框架 UG数量=INTEG(-v0,初始值) (1) KNG数量=INTEG(v0-v1-v2,初始值) (2) TNG-A数量=INTEG(v1+v3+v7-v4-v5,初始值) (3) TNG-B数量=INTEG(v2+v4+v8-v3-v6,初始值) (4) DG-A数量=INTEG(v5-v8,初始值) (5) DG-B数量=INTEG(v6-v7,初始值) (6) v0=UG数量×(DG-A数量+DG-B数量)×α (7) v1=KNG数量×s1 (8) v2=KNG数量×s2 (9) v3=TNG-B数量×s3 (10) v4=TNG-A数量×s4 (11) v5=TNG-A数量×p5 (12) v6=TNG-B数量×p6 (13) v7=DG-B数量×s7 (14) v8=DG-A数量×s8 (15) 其中:式(1)~式(6)表明,当前时刻状态变量的取值是在初始值基础上,初始时刻至当前时刻流入与流出的净值累加;式(7)表明,v0由UG与传播者的数量及α决定[15];式(8)~式(15)表明,群体间的行为状态转移速率与转出群体的数量及其相应的转移概率正相关。 2)信息舆论场反馈作用子框架 信息A传播总量=信息A的平均个体传播量×DG-A数量 (16) 信息B传播总量=信息B的平均个体传播量×DG-B数量 (17) 信息A舆论场的影响力=0.3×信息A可信度+0.7×信息A传播总量 (18) 信息B舆论场的影响力=0.3×信息B可信度+0.7×信息B传播总量 (19) s1=p1×(1+信息A舆论场的影响力/(信息A舆论场的影响力+信息B舆论场的影响力)) (20) s2=p2×(1+信息B舆论场的影响力/(信息A舆论场的影响力+信息B舆论场的影响力)) (21) s3=p3×(1+立场认知水平)×(1+信息A舆论场的影响力/信息B舆论场的影响力) (22) s4=p4×(1-立场认知水平)×(1+信息B舆论场的影响力/信息A舆论场的影响力) (23) s7=p7×(1+信息A舆论场的影响力/信息B舆论场的影响力) (24) s8=p8×(1+信息B舆论场的影响力/信息A舆论场的影响力) (25) 其中:式(16)和式(17)表明,信息传播总量取决于信息的平均个体传播量与传播者数量;式(18)和式(19)表明,信息舆论场的影响力由信息的可信度及其传播总量决定;式(20)~式(25)表明,修正转移概率与初始转移概率正相关,信息A舆论场的影响力可以提高s1,s3,s7和降低s4,s8,信息B舆论场的影响力可提高s2,s4,s8和降低s3,s7,立场认知水平可以提高s3,降低s4。 通过设计和仿真基础情景,并将仿真结果与实际案例进行对比,检验模型的模拟趋势与现实状况的一致性。进一步从决策者的危机管理角度出发,将基础情景作为对照组,通过设计实验情景考查模型中的关键可控因素对系统演化的影响,并据此给出调控策略和建议。 设定UG数量的初始值为1 000;信息A和信息B的发布即为一种传播行为,因此设定DG-A和DG-B数量的初始值均为1;信息A和信息B的出现时刻是群体能否获取这2类信息的时间转折点,因此设定该时刻下KNG、TNG-A和TNG-B的数量均为0;考虑到群体对官方渠道和民间渠道的关注偏好,设定立场认知水平为0.5;信息可信度的取值区间为[0, 100],即取值越高,信息可信度越高,据此将信息A和信息B的可信度分别设定为50;考虑到群体规模和个体传播能力,将单位时间内信息A和信息B的平均个体传播量均设定为4。由于信息A和信息B在出现时刻及发展早期的传播态势较弱,因此未知者与传播者的接触率及其他群体间的初始转移概率不大,不妨设定如下:α=0.01,p1=0.07,p2=0.14,p3=0.06,p4=0.06,p5=0.07,p6=0.09,p7=0.07,p8=0.07。 在此基础上,通过将模型的仿真周期和步长分别设定为40 d和0.2 d,借助Vensim软件对模型的上述基础情景进行仿真,可得到模型中各群体数量的演化趋势,如图5所示。 图5 基础情景中系统演化的仿真结果Fig. 5 Simulation results of system evolution in basic scenario 由图5可知,在系统演化初期(0—13 d),信息B占主导(TNG-A的数量低于TNG-B的数量且DG-A的数量低于DG-B的数量),这是由于突发事件具有突发性和危害性,群体因损失规避,往往倾向于相信和传播信息B;在系统演化后期(24—40 d),信息A占主导(TNG-A的数量高于TNG-B的数量且DG-A的数量高于DG-B的数量),这是由突发事件的逐渐透明、正式或理性信息因被证实而增多、非正式或非理性信息因被证伪而减少及群体认知观念的更新等因素所决定;在系统演化中期(13—24 d),TNG-A的数量高于TNG-B的数量,且差距迅速增大,而DG-A的数量低于DG-B的数量,且差距逐渐缩小,说明信息A和信息B在群体中的地位分别上升和下降。 上述仿真结果符合现实状况。例如:2009年的成都公交纵火事件中,由于造成了人员伤亡,引发了群体的广泛关注,事件发生伊始,虽然搜狐、腾讯等大型媒体及时发布了相关信息A(如:“事件进展”、“公安部门侦查实验”、“政府领导慰问”),但是相关信息B(如:“大火烧死上百人”、“公交车司机不开车门并最早逃跑”、“公交车存在安全隐患、自燃导致起火”)仍然得以在坊间流传并迅速占据了舆论主导。此后,政府接连召开了5次新闻发布会,披露了“死亡20余人”、“公交车非自燃”、“当事司机积极救人”、“汽车发动机完好”、“人为纵火”等信息(即信息A)。随着信息A的数量增多且被证实,信息B逐渐得到澄清而被证伪,信息A逐渐取代信息B而占据舆论主导。 相对于来自民间渠道的信息B,来自官方渠道的信息A更易受决策者监测和调控。鉴于此,进一步研究模型中决策者的关键可控因素(信息A可信度、信息A的平均个体传播量、立场认知水平)的作用机制问题。为此,以基础情景为基准,设计以下3个实验情景。 1)情景1:信息A可信度提高和降低20%(对应情景1-1和情景1-2),仿真结果如图6所示。可见提高信息A可信度可显著增多TNG-A和DG-A,并可显著减少TNG-B和DG-B,尤其是第13 d后(即系统演化中期和后期),而降低信息A可信度的作用恰恰相反。因此,发布信息A的官方渠道不仅应该注重提升自身的公信力,还应该注重一手数据的获取、信息撰写规范性的优化和群体对信息易接受表达方式的研判,提升信息A的可信度及其对信息B的抑制作用。 图6 信息A可信度对系统演化的影响Fig. 6 Effect of credibility of Information A on system evolution 图7 信息A的平均个体传播量对系统演化的影响Fig. 7 Effect of AIDQ of Information A on system evolution 图8 立场认知水平对系统演化的影响Fig. 8 Effect of CLPG on system evolution 2)情景2:信息A的平均个体传播量提高和降低20%(对应情景2-1和情景2-2),仿真结果如图7所示。可见与信息A可信度相比,信息A的平均个体传播量对系统演化的影响规律类似,但影响更为显著。随着新媒体和4G网络的普及,移动设备日益成为人们获取信息和抒发情绪的首选。在此新形势下,非正式或非理性的信息B出现概率被大幅提升,因此决策者应该鼓励社交网络中的“大V”积极传播信息A,引领民众,主动占据舆论制高点,规避信息B恶意传播造成的潜在危机。 3)情景3:立场认知水平提高和降低20%(对应情景3-1和情景3-2),仿真结果如图8所示。可见与上述2个因素相比,立场认知水平对系统演化影响的显著性较弱,但影响规律仍类似。新媒体具有双向互动和准入门槛低等特点,易积聚信息B并诱发群体恐慌。为此,决策者一方面应该督促新媒体运营商主动倡导正面舆论和调控负面舆论,另一方面应该增强历史案例的宣传、负面舆论的危害警示和群体关切的及时回应,提高群体在突发事件爆发后关注与信任官方渠道的意识。 1)将系统动力学的应用扩展到突发事件下的多种信息共存情境,建立信息交互关系框架和系统动力学模型,为研究该情境中信息间的交互规律、动力机制和调控策略提供思路。 2)官方渠道所发布信息的可信度、平均个体传播量及群体的立场认知水平,与相信和传播官方渠道信息的人数均正相关,而与相信和传播民间渠道信息的人数均负相关。 3)对于各群体数量演化影响的显著性而言,官方渠道信息的平均个体传播量最高,官方渠道信息的可信度次之,群体的立场认知水平较低。 4)多种信息间除了具有异质性或竞争性关系,还具有同质性或叠加性关系,故多种同质性信息共存情境或多种异质性和同质性信息共存情境中的群体状态耦合机制问题仍需深入研究。 [1]RACHANIOTIS N P, DASAKLIS T K, PAPPIS C P. A deterministic resource scheduling model in epidemic control: A case study[J]. European Journal of Operational Research, 2012, 216(1): 225-231. [2]刘怡君,陈思佳,黄远,等. 重大生产安全事故的网络舆情传播分析及其政策建议—以“8·12天津港爆炸事故”为例[J]. 管理评论,2016,28(3):221-229. LIU Yijun, CHEN Sijia, HUANG Yuan, et al. The analysis and policy recommendations on the spread of network public opinion in major production safety accidents: A case study of the 8·12 Tianjin port explosion[J]. Management Review, 2016, 28(3): 221-229. [3] 陈业华,康亚红,宋之杰. 公共场所突发事件情境下受灾人群间信息的传播与扩散研究[J]. 数学的实践与认识,2015,45(16):44-54. CHEN Yehua, KANG Yahong, SONG Zhijie. The research of information dissemination and diffusion between the affected people in the scenario of public places emergencies[J]. Mathematics in Practice and Theory, 2015, 45(16): 44-54. [4] 武澎,王恒山,李煜. 突发事件信息传播超网络中枢纽节点的判定研究[J]. 管理评论,2013,25(6):104-111. WU Peng, WANG Hengshan, LI Yu. Determination of the hub nodes in the emergencies’ information dissemination supernetwork[J]. Management Review, 2013, 25(6): 104-111. [5] OU C, JIN X, WANG Y, et al. Modelling heterogeneous information spreading abilities of social network ties[J]. Simulation Modelling Practice and Theory, 2017(75): 67-76. [6]ZHANG Y, TANG C, LI W. Cooperative and competitive dynamics model for information propagation in online social networks[J]. Journal of Applied Mathematics, 2014(2): 1-12. [7]WANG J, ZHAO L, HUANG R. 2SI2R rumor spreading model in homogeneous networks[J]. Physica A: Statistical Mechanics and its Applications, 2014, 413(1): 153-161. [8]XIE M, JIA Z, CHEN Y, et al. Simulating the spreading of two competing public opinion information on complex network[J]. Applied Mathematics, 2012, 3(9): 1074-1078. [9]XU J, ZHANG L, MA B, et al. Impacts of suppressing guide on information spreading[J]. Physica A: Statistical Mechanics and its Applications, 2016(444): 922-927. [10]王治莹,岳朝龙. 舆情传播中考虑公众风险感知的多资源流应急优化调度[J]. 中国管理科学,2016,24(6):115-123. WANG Zhiying, YUE Chaolong. Emergency optimal scheduling of multi-resource flow considering the public’s risk perception in public opinion propagation[J]. Chinese Journal of Management Science, 2016, 24(6): 115-123. [11]MORALES A J, BORONDO J, LOSADA J C, et al. Efficiency of human activity on information spreading on Twitter[J]. Social Networks, 2014, 39(1): 1-11. [12]王治莹,李勇建. 政府干预下突发事件舆情传播规律与控制决策[J]. 管理科学学报,2017,20(2):43-52,62. WANG Zhiying, LI Yongjian. Propagation law and coping strategies for public opinions in emergency with the consideration of the government intervention[J]. Journal of Management Sciences in China, 2017, 20(2): 43-52, 62. [13]FRIEDKIN N E, PROSKURNIKOV A V, TEMPO R, et al. Network science on belief system dynamics under logic constraints[J]. Science, 2016, 354(6310): 321-326. [14]DEYOUNG S E, WACHTENDORF T, FARMER A K, et al. NOAA radios and neighbourhood networks: demographic factors for channel preference for hurricane evacuation information[J]. Journal of Contingencies and Crisis Management, 2016, 24(4): 275-285. [15]OSTHUS D, HICKMANN K S, CARAGEA P C, et al. Forecasting seasonal influenza with a state-space SIR model[J]. The Annals of Applied Statistics, 2017, 11(1): 202-224.2.2 因果回路图
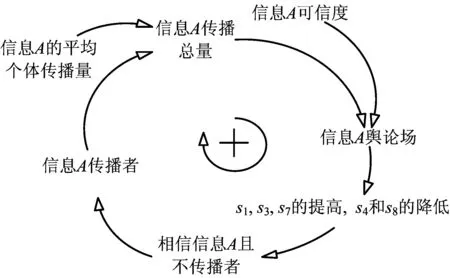
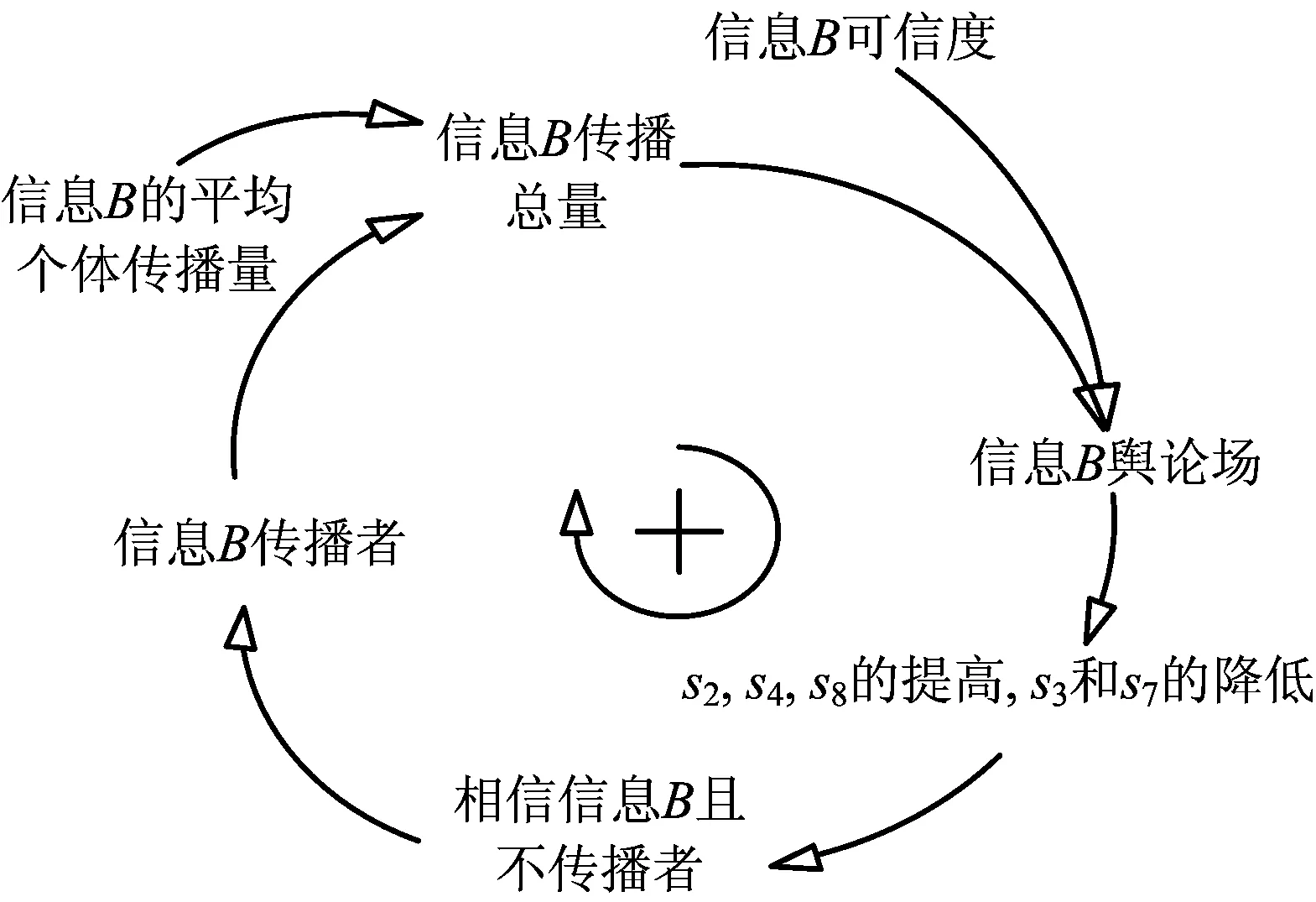
2.3 存量流量图
3 情景仿真
3.1 基础情景仿真
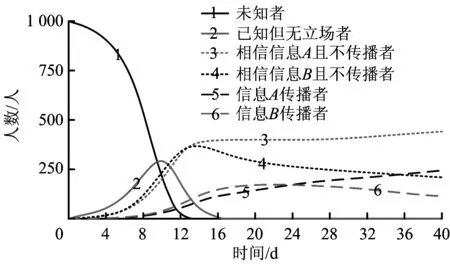
3.2 实验情景仿真
4 结论

