走滑断层作用下X80管道设计应变规律和神经网络预测*

郑　倩，张　宏，张克政，刘啸奔，夏梦莹，吴　锴，王宝栋

(1. 中国石油大学(北京) 机械与储运工程学院，北京 102249；2. 中海石油气电集团有限责任公司，北京 100028)

0　引言

活动断层是管道穿越地震区的主要威胁，断层作用下管道会因较大的应变而失效。因此，预测管道在断层作用下的应变对跨断层区管道的设计与安全评估具有重要意义[1]。

在断层下管道响应研究领域，Newmark-Hall法、Kennedy法和Karomitros法是较具代表性的解析方法。前2种方法均采用“索”模型来模拟管道[2-3]，管道只能承受轴向的拉伸而不能承受侧向的弯矩，因此只能在穿越角小且断层位移较大(即管道主要受轴向拉伸)时才能得到比较准确的结果[4]。而Karamitros法考虑了管道刚度的变化，采用弹性梁-弹性地基梁模型可较准确地计算出走滑断层下管道受拉时的设计应变[4-5]。由于解析方法中基本假设的局限性，有限元方法被更加广泛地用于准确计算管道的各种力学响应，并根据其计算结果开展管道力学响应规律的分析[6]。刘啸奔等[7]基于非线性有限元软件，利用管单元 -弯管单元计算了X80管道穿越走滑断层时的最大压应变，提出了半经验应变预测模型。

解析法的计算较为快捷，但准确性不高，且只能适用于管道受拉伸情况，对于管道压缩时完全不适用，也无法分析管道的屈曲行为。有限元法因计算结果的准确性而得到广泛应用，但该方法计算时间长，对计算机硬件要求高，且建模过程也较复杂。2013年，SHOKOUHI等[8]将神经网络用于地震作用下管道应变的计算，该方法基于限元模型的计算结果对神经网络进行训练，训练好的网络可准确预测管道的应变，但其有限元模型中并未准确考虑土壤特性参数对管道应变的影响，因此与真实工况会有一定误差；李剑楠[9]将神经网络用于埋地管道的可靠性分析中，利用神经网络预测了断层场地下管道的最大轴向应力值，但其训练样本中最大轴向应力值并非通过计算准确的有限元法获得，而是利用Newmark-Hall解析方法计算而来，而目前的有限元计算已表明，Newmark-Hall法在管道穿越角度较大时的结果过于不保守。因此，该网络模型的预测结果具有局限性。人工神经网络具有高度非线性运算能力，能对复杂的数学模型进行预测，是解决隐式问题的有效方法，被广泛应用于多个领域。在管道方面，神经网络多用于管道腐蚀问题的研究，多数学者均采用神经网络预测管道的腐蚀速率[10]、腐蚀剩余强度[11]及其爆破压力[12]等，而利用神经网络预测管道在地质灾害作用下的应变较少。基于此，本文以走滑断层下的X80管道为研究对象，建立了管道应力应变计算的有限元模型；分析了管径、壁厚、内压、断层位移以及土弹簧极限抗力对管道轴向最大拉、压应变的影响；基于数值计算结果，采用神经网络建立起管道设计应变的预测模型。

1　走滑断层下管道的有限元模型

图1为管道穿越走滑断层的示意图，断层引起地表错动从而导致管道发生变形，如图1所示，管道穿越角β为90°，管道的轴向为x方向，侧向为y方向，管道在该断层下主要受到拉伸和弯曲作用。

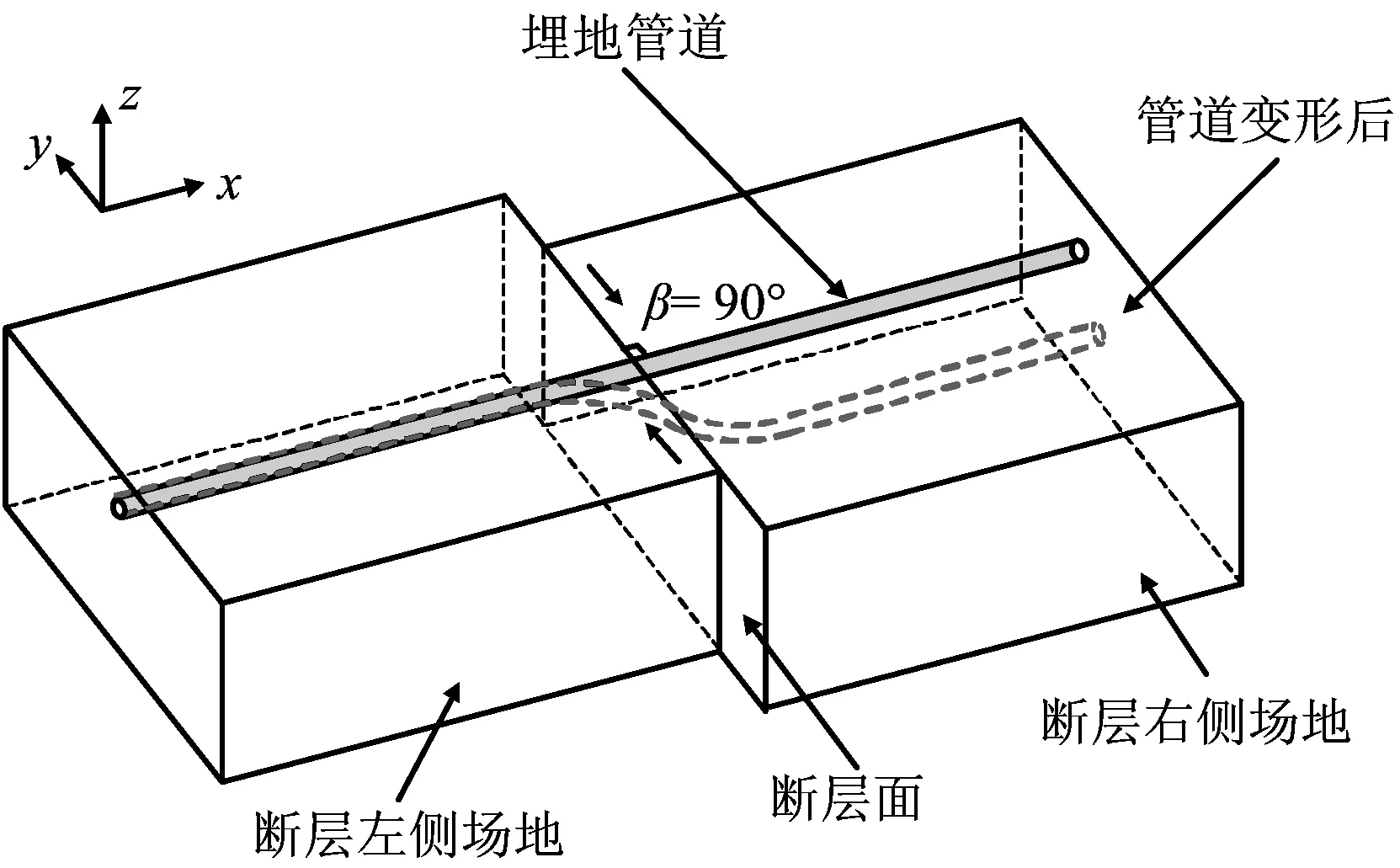
图1　管道穿越断层示意Fig.1　Sketch of pipe subjected to strike-slip fault displacement.

为准确模拟断层附近管道的力学响应，本文采用ABAQUS软件提供的Jointc单元来模拟土弹簧，采用管壳耦合的方式建立了对应的有限元模型。模型中管道分为2部分，管道总长取2 100 m，利用壳单元模拟断层两侧100 m范围内管道，环向分为24个节点，沿轴向每0.2 m 1个单元；剩余部分管道采用管单元模拟，每1 m 1个单元，使用耦合单元将管单元和壳单元连接起来，各向土弹簧与单元节点相连，图2为本文有限元模型的示意图。

Ramberg-Osgood模型能较好地描述高强钢管道的力学性能[9]，用该模型对X80钢管材料拉伸实验结果的应力-应变曲线进行拟合，得到如表1所示的拟合参数。

表1　X80管材特性取值

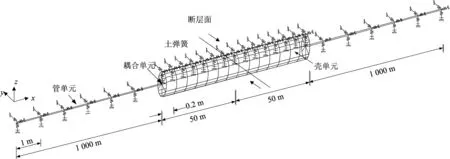
图2　走滑断层下有限元模型示意Fig.2　Simplified FE model of a pipeline crossing a strike-slip fault

2　参数分析

本文主要参考西二线工程确定各参数取值，部分参数取值范围如表2所示。同时结合我国国情需要，补充了外径为1 422 mm管道的相关参数。

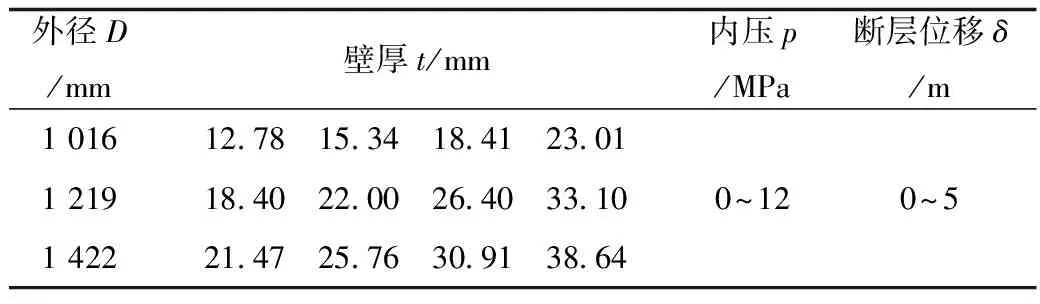
表2　影响因素的取值范围

走滑断层下，仅轴向、侧向土弹簧会对管道产生作用力。参数分析中，考虑轴向、侧向土弹簧极限抗力取值的相关性，从而保证计算所用的土壤极限抗力的范围更贴近实际工况。根据ALA-ASCE 2001附录B中推荐的公式，采用表3中砂土的土壤参数，计算得到工程中管道可能受到的土弹簧轴向和侧向土弹簧极限抗力的取值范围如图3所示。

表3　砂土特性参数取值范围

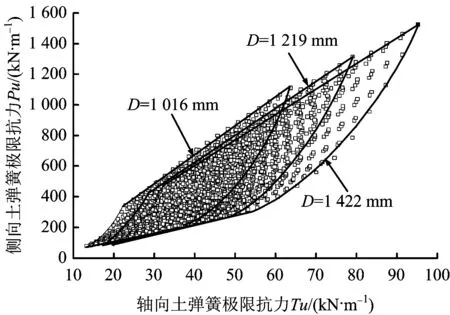
图3　轴向和侧向土弹簧极限抗力取值范围Fig.3　Range of Tu and Pu

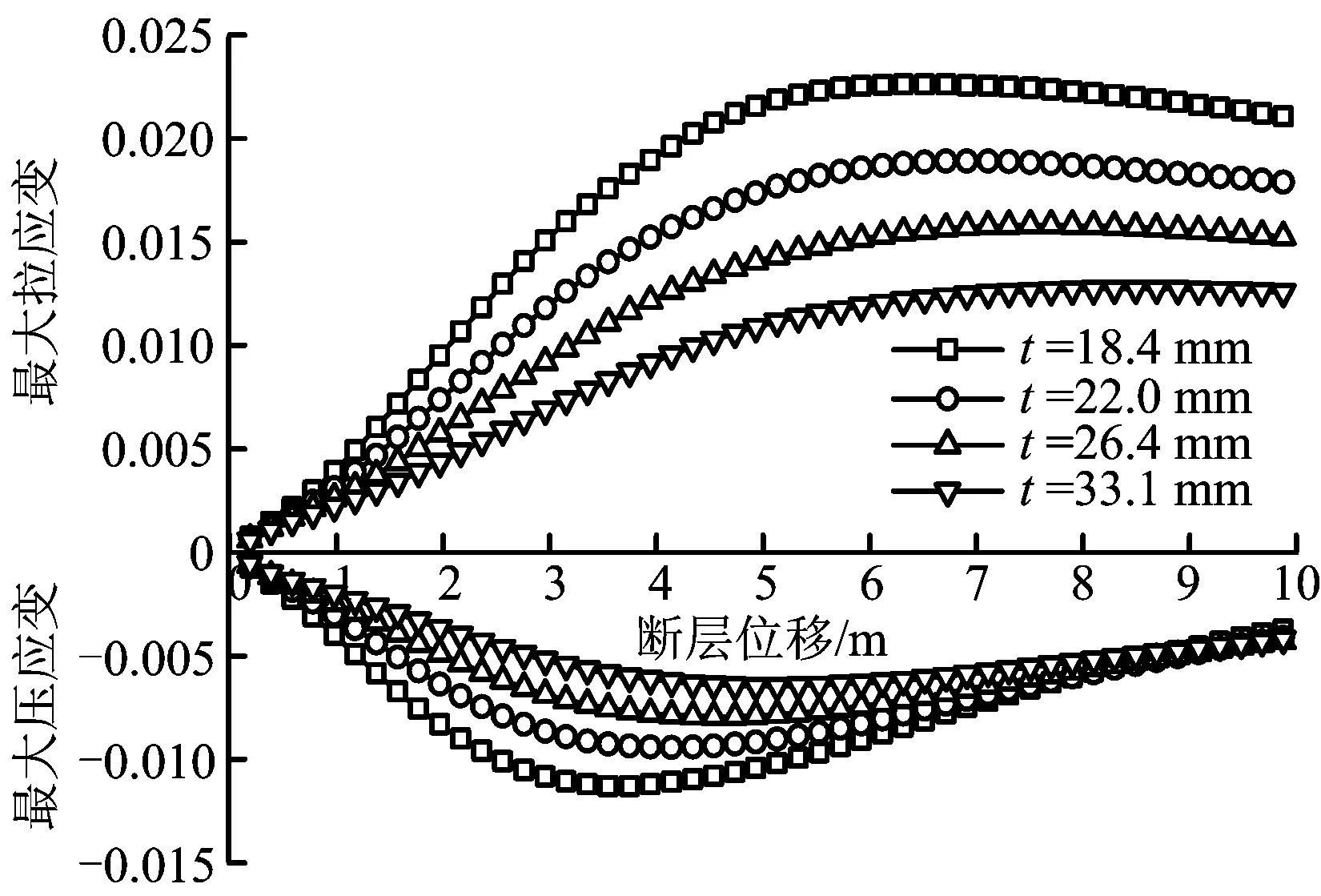
图4　不同壁厚下设计应变随断层位移的变化规律(φ 1 219 mm)Fig.4　Relationship between design strain and fault displacement with different pipe wall thicknesses(φ 1 219 mm)

2.1　管径和壁厚的影响

图4为φ 1 219 mm管道的设计应变在不同壁厚下随断层位移的变化规律。图4显示，壁厚越大，在同一断层位移下的设计应变越小。因此，壁厚的增大有助于管道抗震。但最大拉应变与最大压应变随断层位移变化的趋势不同，断层位移增大时，最大拉应变呈“逐渐增长→趋于平缓→逐渐减小”的趋势，而最大压应变呈“逐渐增长→逐渐减小”的变化，且壁厚越大，设计应变峰值越小，设计应变平缓段越长。在同一断层位移下，管道的最大拉应变总是高于最大压应变。因此，在穿越角为90°的走滑断层下，管道主要受到拉伸作用。

管道设计应变由轴心应变与弯曲应变控制。断层位移较小时，管道弯曲应变较大，轴心应变几乎为零。随着断层位移的增加，管道整体呈伸长趋势，在协调条件下，管道轴心应变逐渐增大。随着断层位移的进一步增加，管道弯曲段的曲率几乎不变，此时弯曲应变较小，而更多管道进入弯曲段，轴心应变逐渐降低。因此，导致整个管道的最大拉应变逐渐变小。同小壁厚管道相比，相同外径下的大壁厚管道的弯曲刚度和轴向刚度均增加，因此，具有更强的抵抗变形的能力，在应变规律上体现出具有更小的设计应变峰值和更长的应变平缓段。

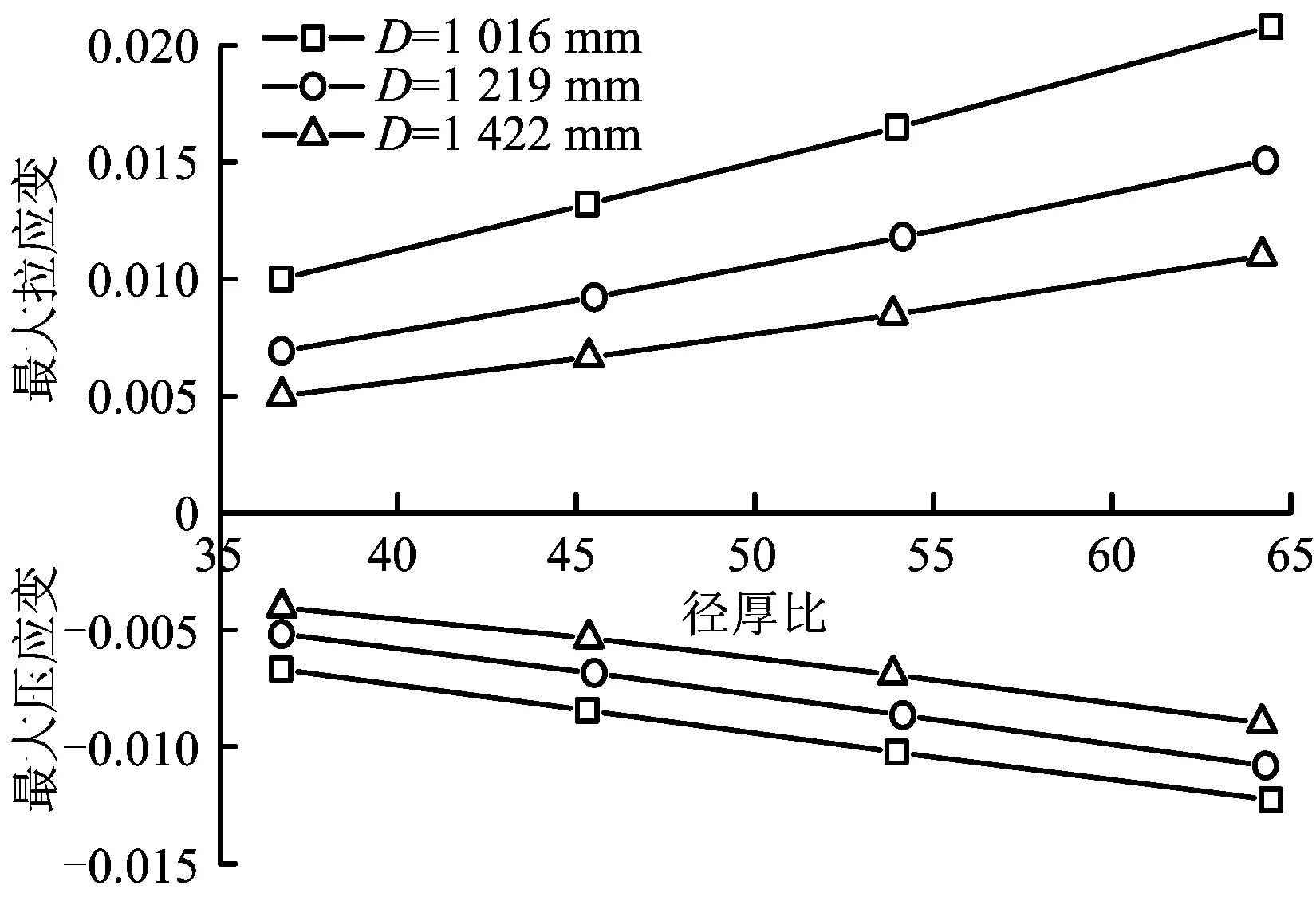
图5　不同管径下设计应变随径厚比的变化规律(δ=3 m)Fig.5　Relationship between design strain and D/t with different pipe diameters(δ=3 m)

图5为设计应变与径厚比的关系，从该图中可定性分析管径对设计应变的影响。图5显示，在径厚比相等的情况下，管径越大，设计应变越小。因此，可定性分析得大管径的抗震能力更强，且设计应变与径厚比近似呈线性关系。

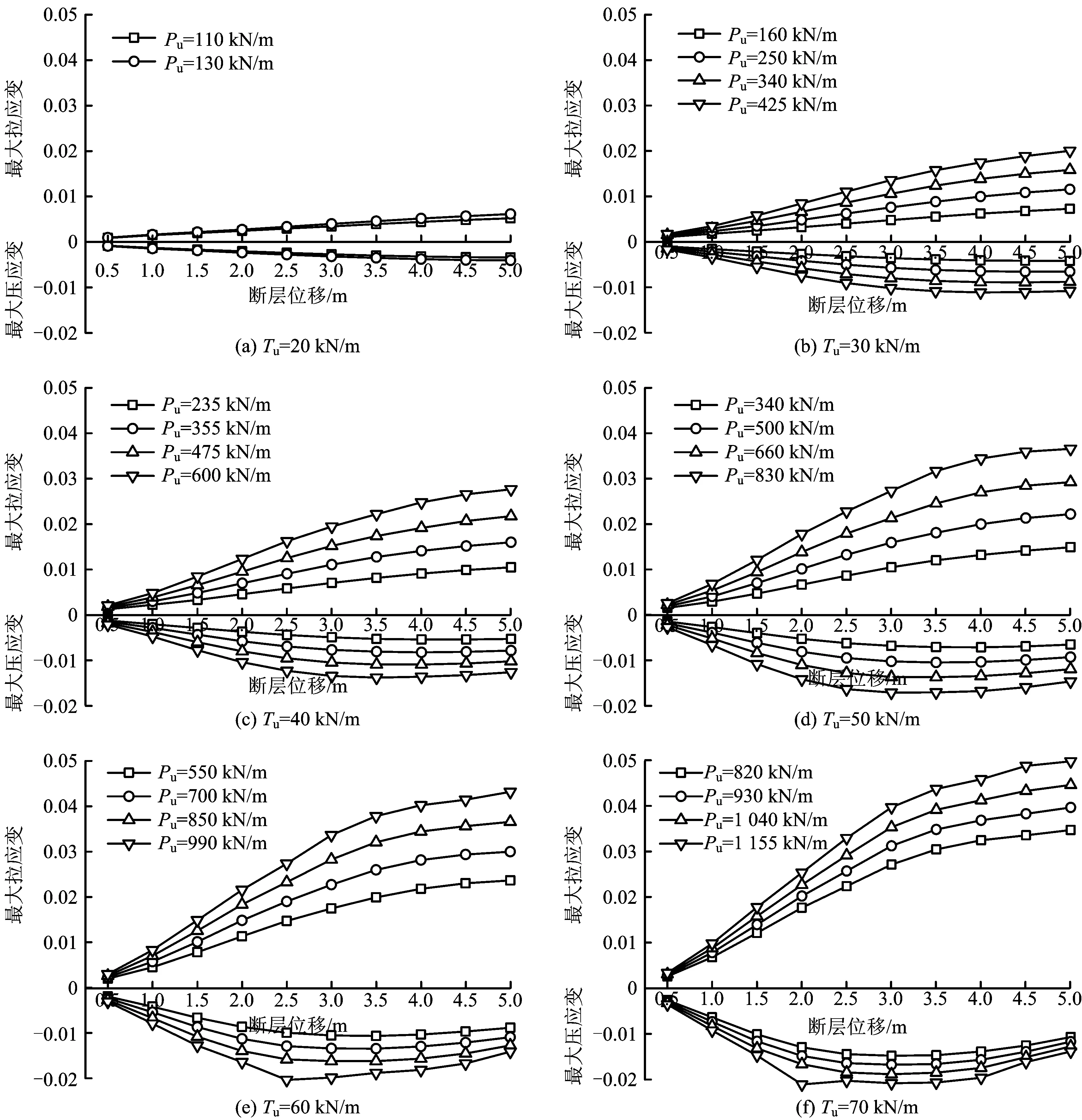
图7　不同土弹簧极限抗力下设计应变随断层位移的变化规律(φ 1 219 mm×22 mm)Fig. 7　Relationship between design strain and fault displacement with different ultimate resistance of soil springs(φ 1 219 mm×22 mm)

2.2　内压的影响

根据表2给出的内压范围，以φ 1 219 mm × 22 mm管道为例分析内压对设计应变的影响。内压取值为0，2，4，6，8，10和12 MPa，分析结果如图6所示。图6显示，管道的设计应变随内压的增大而增大，但内压对应变的影响并不显著，甚至在小位移下(δ≤1 m)，内压对管道的设计应变几乎无影响。

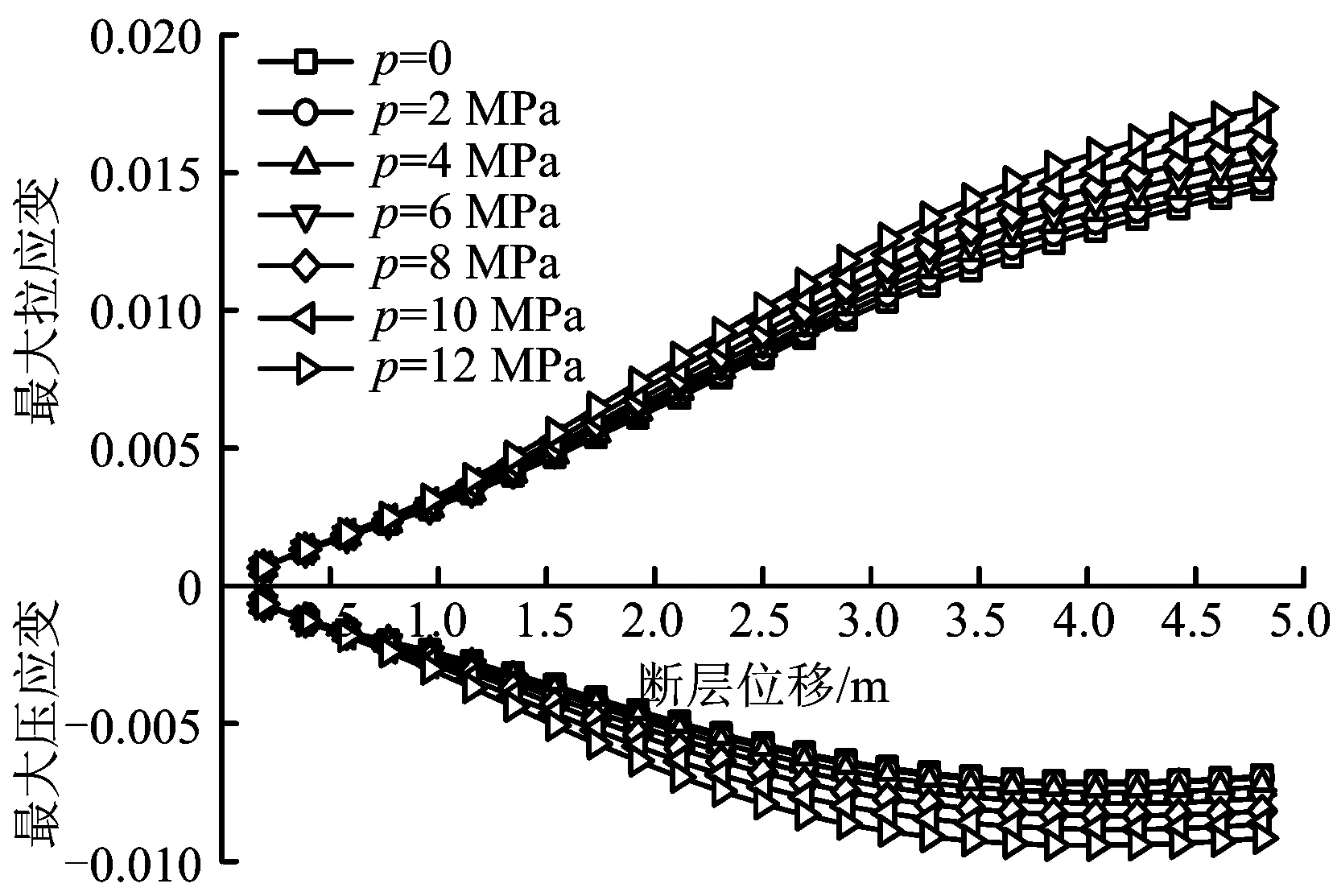
图6　不同内压下设计应变随断层位移的变化规律Fig. 6　Relationship between design strain and fault displacement with different internal pressures

2.3　土壤的影响

根据图3中确定的土弹簧极限抗力范围，得到如图7所示的不同土弹簧极限抗力组合下设计应变随断层位移的变化规律。

当轴向土弹簧极限抗力相等时，在相同断层位移下，侧向土弹簧极限抗力越大，设计应变也越大。这是因为土弹簧极限抗力越大，在相同断层位移下，土壤对管道的作用力就越大，因而设计应变也越大，越不利于管道抗震。

3　BP神经网络预测

人工神经网络技术是对大脑功能的模拟、抽象和简化[13]，具有学习、联想和记忆功能，以及高度的非线性预测能力。BP神经网络属于多层前馈网络，网络训练时信号前向传递，误差反向传播，根据预测误差，采用梯度下降法调整网络的权值和阈值，使预测输出不断逼近期望输出[14]。本文利用BP双隐层神经网络对走滑断层下穿越角为90°的X80管道的设计应变进行预测，双隐层网络包含2个单隐层，同单隐层相比，多隐层网络具有更强的泛化能力和更高的预测精度[15]。

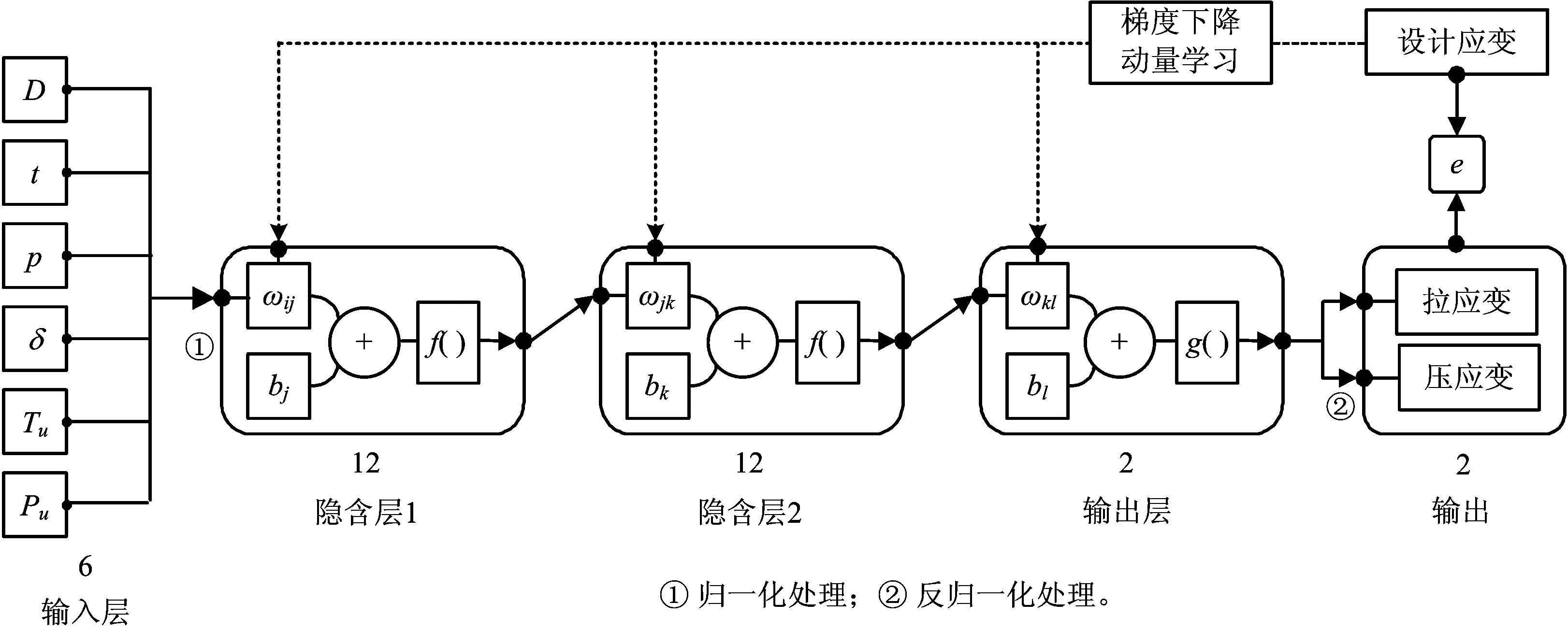
图8　BP双隐层神经网络的结构Fig. 8　The structure of BP double hidden layer neural network

为了全面分析管径、壁厚以及内压因素对设计应变的影响，在第2.1节和第2.2节计算工况总数为3×4×7×25=2 100个(其中，3指管径取3个值；4指每个管径下的壁厚取4个值；7指内压取7个值；25为断层位移取25个值)，包括了X80所有管道在不同内压和断层位移条件下的工况。

在分析土弹簧极限抗力对设计应变的影响时，为减少计算成本，断层位移设定为10个，且由第2.2节分析可得，内压对管道设计应变的影响很小。因此，内压设定为12 MPa。该项分析中，算例总数为(20+23+25)×4×1×10=2 720(其中，20，23，25分别为指管径为1 016 mm，1 219 mm，1 422 mm的土弹簧极限抗力组合取值个数；4指各管径下的壁厚分别取4个值；1为内压取1个值，内压值为12 MPa；10是指断层位移取10个值)，包括了X80不同管道在不同断层位移条件下的工况。由此可知，以上参数计算包含了X80管道在不同内压、不同断层位移以及不同轴向、侧向土弹簧极限抗力组合条件下的工况，因此，该数据库涵盖了多因素影响下的工况，能对神经网络进行充分的训练。

3.1　网络的结构和训练

根据走滑断层下管道破坏原因，在穿越角为90°时，影响X80管道的应变因素主要包括管径(D)、壁厚(t)、内压(p)、断层位移(δ)、轴向土弹簧极限抗力(Tu)及侧向土弹簧极限抗力(Pu)等6个因素。因此，将其作为网络输入层的6个神经元。将最大拉应变(εTmax)和最大压应变(εCmax)作为输出层的2个神经元。隐含层个数根据式(1)初步确定[16]：

(1)

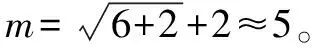
网络隐含层传递函数选用双曲正切S型传递函数tansig，该函数将输出控制在[-1,1]范围内，可将数据统一成一个量级，避免了计算中不必要的数值问题；输出层采用线性传递函数purelin[17]。训练函数选用trainlm，即Levenberg-Marquardt优化算法，该算法兼具牛顿法和共轭梯度法的优点，能够加快网络的收敛速度[18]。

按照以上设定，采用MATLAB编程创建网络。网络的训练样本总数为4 817组(有限元工况总数4 820与计算不收敛组数3的差值)，网络结构如图8所示。经过多次训练和计算，最终确定回归效果最优的网络，此时网络的回归系数为0.999 92，说明网络训练后的预测效果良好。根据Kolmogrov定理，网络节点数确定为12。

因此，网络最终结构为6-12-12-2，训练最大步数50，训练速率0.1，误差平方和2×10-5。样本总体数据的训练效果如图9所示。

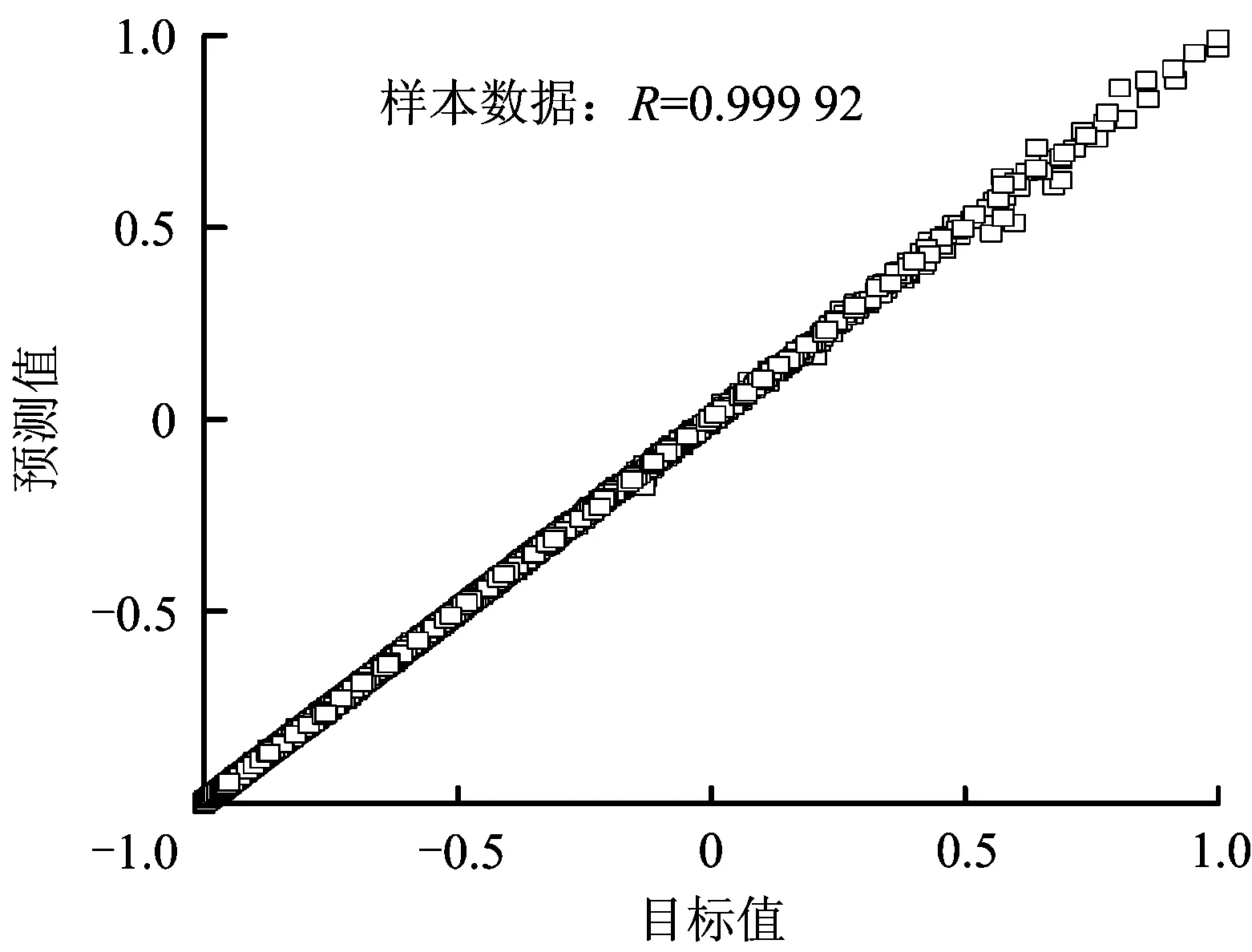
图9　网络训练结果Fig 9　The results for network training

3.2　神经网络预测效果的验证

为验证网络预测的准确性，采用训练样本以外的20组数据代入网络进行预测，预测样本中各物理量除管径、壁厚外，其他各参数应随机取值，取值既不与训练样本数据相同，又满足实际工况的要求。图10为该20个样本的网络预测结果。

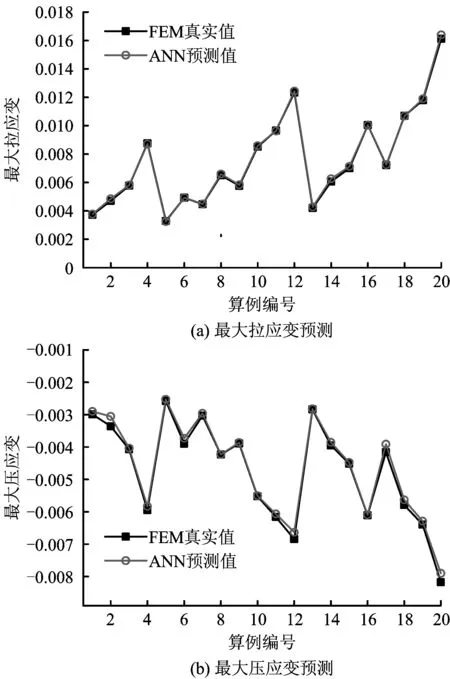
图10　神经网络的预测结果Fig. 10　The results for predictions of neural network

图10显示，网络预测值与真实值之间相差较小，且预测结果和真实结果的变化趋势相同，表示该神经网络模型得到充分的训练，其中，最大拉应变预测的相对误差最大为3.31%(算例7)，最大压应变预测的相对误差最大为8.97%(算例12)，该网络预测结果的最大相对误差小于10%。因此，可以认为网络的预测效果良好。

在对以上算例进行预测时，分别记录了有限元计算和神经网络预测所用的时间。有限元计算CPU time为3 387.4 s，而神经网络预测CPU time为0.06 s，瞬间可获得应变结果。可见，神经网络在时间成本上较有优势，尤其适合可靠性设计中的海量计算。

4　结论

1)管道以90°穿越角穿越走滑断层时主要受拉伸作用，而最大拉、压应变随断层位移的增长并非呈单调增的趋势；当断层位移超过某一值时，最大拉应变不再增加，而最大压应变随断层位移的增长会出现极大值。管径、壁厚的增大以及土弹簧极限抗力的减小更有助于管道抗震，而内压几乎不影响管道的设计应变。

2)基于4 817组有限元结果，创建了用于走滑断层作用下X80管道设计应变预测的神经网络模型，验证结果表明，该模型能准确预测管道的最大拉、压应变，预测结果的最大相对误差小于10%。

3)神经网络的应用克服了有限元法计算时间长、硬件设施高和须要建模经验丰富的专业人员的缺陷，其应用方式简单，计算速度快，预测精度高，为断层作用下管道的设计应变提供较为便捷的预测方式，尤其为断层作用下管道基于应变的可靠性分析提供了更加便捷的计算方式，对工程应用有一定的参考价值。

[1] 刘啸奔，陈严飞，张宏，等．跨断层区X80钢管道受压时的设计应变预测[J]．天然气工业，2014，34(12)：123-130.

LIU Xiaoben, CHEN Yanfei，ZHANG Hong，et al. Prediction on the design strain of the X80 steel pipelines across active faults under stress[J]. Natural Gas Industry, 2014,34(12):123-130.

[2]NEWMARK NM, HALL WJ. Pipeline design to resist large fault displacement[C]// Ann Arbor. Proceedings of the U.S. National Conference On Earthquake Engineering, 1975: 799-807.

[3] KENNEDY R P, DARROW A W, WILLIAMSON R A. Fault movement effects on buried oil pipeline[J]. Transport Engineering Journal, 1977, 103(5): 617-633.

[4]韩银杉，张宏．走滑断层作用下管道应变解析计算方法的适用性[J]．油气储运，2016，35(12)：1329-1336.

HAN Yinshan, ZHANG Hong. Applicability of analytical calculation methods on the pipeline strain under the effect of strike-slip fault[J]. Oil & Gas Storage and Transportation, 2016，35(12):1329-1336.

[5]KARAMITROS D K, BOUCKOVALAS G D, KOURETZIS G P. Stress analysis of buried steel pipelines at strike-slip fault crossings[J]. Soil Dynamics and Earthquake Engineering, 2007, 27(3): 200-211.

[6]刘啸奔，张宏，李勐，等．断层作用下埋地管道应变分析方法研究进展[J]．油气储运，2016，35(8)：799-807.

LIU Xiaoben, ZHANG Hong, LI Meng, et al. Research progress of strain analysis methods for buried pipelines under faulting process. Oil & Gas Storage and Transportation, 2016, 35(8):799-807.

[7] LIU X B，ZHANG H，HAN Y S，et al. A semi-empirical model for peak strain prediction of buried X80 steel pipelines under compression and bending at strike-slip fault crossings[J]. Journal of Natural Gas Science and Engineering, 2016, 32(32): 465-475.

[8]SHOKOUHI S K, DOLATSHAH A, GHOBAKHLOO E. Seismic strain analysis of buried pipelines in a fault zone using hybrid FEM-ANN approach[J]. Earthquakes and Structures, 2013, 5(4): 417-438.

[9]李剑楠. 基于人工神经网络模型的埋地管道可靠性研究[D]. 唐山：华北理工大学, 2016.

[10]陶翠翠．改进BP神经网络在埋地金属管道腐蚀速率预测中的应用[C]//第七届沈阳科学学术年会暨浑南高新技术产业发展论坛论文集，沈阳，2010：453-458.

[11]冯志刚. 输油管道的腐蚀检测与剩余强度评价[D]. 西安：西安石油大学，2007.

[12] XU Wenzheng, LI Chunbao, CHOUNG J, et al. Corroded pipeline failure analysis using artificial neural network scheme[J]. Advances in Engineering Software, 2017, 112: 255-266.

[13] 王原嵩. 基于GA-BP神经网络的海底腐蚀管道极限承载力研究[D]. 大连：大连理工大学, 2009.

[14] 汪送，王瑛，李超．BP神经网络在航空机务人员本质安全程度评价中的应用[J]．中国安全生产科学技术，2010，6(6)：35-39.

WANG Song, WANG Ying, LI Chao. Application of BP neural network in inherent safety degree evaluation of aviation maintenance personnel[J]. Journal of Safety Science and Technology, 2010, 6(6):35-39.

[15]王小川，史峰，郁磊，等．MATLAB神经网络43个案例分析[M]．北京：北京航空航天大学出版社，2013.

[16]管志川, 胜亚楠, 许玉强,等. 基于PSO优化BP神经网络的钻井动态风险评估方法[J]. 中国安全生产科学技术,2017, 13(8):5-11.

GUAN Zhichuan, SHENG Yanan, XU Yuqiang, et al. Dynamic risk assessment method of drilling based on PSO optimized BP neural network[J]. Journal of Safety Science and Technology, 2017, 13(8):5-11.

[17]飞思达科技产品研发中心. 神经网络理论与MATLAB7实现[M]. 北京： 电子工业出版社, 2005.

[18]赵弘，周瑞祥，林廷圻．基于Levenberg-Marquardt算法的神经网络监督控制[J]．西安交通大学学报，2002，36(5)：523-527.

ZHAO Hong, ZHOU Ruixiang, LIN Tingqi. Neural network supervised control based on Levenberg-Marquardt Algorithm[J]. Journal of Xi’an Jiaotong University, 2002, 36(5):523-527.